To historians of mechanics, Guidobaldo del Monte presents something of a
paradox. On the one hand, he attempted to found mechanics on the strictest
principles of abstract, Archimedean statics. On the other, he insisted that
mechanics was not a purely abstract, mathematical science, but rather was
essentially concerned with actual machines. He vigorously criticized Tartaglia
despaired [...] of there ever being a mathematical science of dynamics and himself erected unbridgeable barriers between dynamics and mathematical statics. (Rose 1975, 229)
But as Maarten Van Dyck
Given that Guidobaldo had adopted the equilibrium of centers of
gravity as the sovereign principle in mechanics, how did he attempt to apply
it to the actual motion of real machines? And how did his choice of this
principle determine the nature and scope of the mechanics that followed from
it? To answer these questions I shall first look at the application of the
principle to the simple machines in Guidobaldo’s Mechanicorum liber (1577),
his major mechanical work. His other published work on mechanics, the
Paraphrase of Archimedes’s
But before I turn to the Mechanicorum liber, I should like to sketch briefly
the state of mechanics before Guidobaldo. The work that set the scope and
program of mechanics and gave the first definitive content to the nascent
science in the sixteenth century was the pseudo-Aristotelian Mechanica (or Quaestiones mechanicae). In its introduction, the
Mechanica reduced mechanical marvels to the balance and ultimately to
the marvelous properties of the circle. Analyzing the movement of the ends of
the balance into a natural and a violent or preternatural component, it argued
that a power is swifter and thus more effective the greater its natural
component over its violent. For this reason a weight or a power is more
effective the longer the arm of the balance, since the longer arm partakes
more of the natural than the violent movement. This principle of circular
movement was then applied to a number of questions, the first few concerning
the balance and the lever, later ones taking up the wheel, the wedge, pliers,
and the like, including a number of questions on topics such as the motion of
heavy bodies, projectile motion, and whirlpools that have little or nothing to
do with the principle of circular movement. The Mechanica was translated into
Latin early in the sixteenth century and was the subject of several
commentaries and paraphrases by mid-century, including an influential
paraphrase and commentary by Alessandro Piccolomini
At the same time as the pseudo-Aristotelian Mechanica was becoming more widely known, the
medieval science of weights (scientia de ponderibus), represented
especially by the works attributed to Jordanus de Nemore
The Mechanicorum liber thus
has six parts or treatises, the first devoted to the demonstration of the
principle of equilibrium of the balance, the subsequent five to the lever,
pulley, wheel and axel, wedge, and screw. The first part has already been treated
elsewhere in detail by Vico Montebelli
That speed and motion are results, not the causes, of equilibrium and disequilibrium Guidobaldo states explicitly in the corollary to Proposition 6 of the first treatise, De libra (On the Balance). In Proposition 5 Guidobaldo had proved the central theorem of equilibrium, that weights are in equilibrium when their distances from the center are inversely as their weights. In Proposition 6 he then proves that equal weights weigh in proportion to their distances from the center. And from this follows the corollary that, since the farther a weight is from the center of the balance the heavier it will be, so its motion will be the swifter. Relegated to a corollary, speed and motion are thus the results, not the causes, of greater or lesser heaviness.13
Having established in these first propositions the principle of
the equilibrium of the balance, Guidobaldo then applied it in turn to each of
Heron’s
For the space of the power has the same ratio to the space of the weight as that of the weight to the power which sustains the same weight. But the power that sustains is less than the power that moves; therefore the weight will have a lesser ratio to the power that moves it than to the power that sustains it. Therefore the ratio of the space of the power that moves to the space of the weight will be greater than that of the weight to the power.14
The conditions of equilibrium having been established, motion is produced only
by the addition of some indefinite amount of power. Notice that Guidobaldo has
no aversion to comparing the spaces moved by powers and weights, in exactly
the way that Jordanus
In the treatises on the pulley, on the wheel and axel, and on the screw,
Guidobaldo also introduced the time taken to move the weight and its speed,
noting that the more easily a power can move a weight, the more slowly it does
so.15
In his treatises on the wedge and on the screw,
Guidobaldo cited Pappus’s
In the Meditatiunculae, Guidobaldo sketched his own version of
Pappus’s
Despite his general emphasis on equilibrium, motion and its effects do find
their way into his mechanics, notably in his treatment of the wedge, but only
as secondary causes. In the Mechanicorum liber, after attempting to
reduce the wedge to a pair of levers and thus account for its effectiveness,
Guidobaldo adds the power of the blow striking it as another explanation. The
power of the blow, he explains, depends both on the weight of the hammer and
the distance through which the hammer moves, which is greater the longer the
handle. The longer the handle, then, effectively the heavier the hammer and so
the stronger the impulse of the blow. So far these effects can be seen to
arise from the properties of the lever and thus the balance. But then he adds
that the effectiveness of the wedge also arises in part from the very strong
force of percussion, citing Question 19 of the Mechanica, which in
fact his explanation echoes. Here he has moved entirely away from equilibrium
as the cause of a mechanical effect and invoked the unexplained power of
percussion.20
Each of the separate treatises on four of the five
simple machines ends with Heron’s
Since the powers that move may be infinite [in number], one cannot give a firm rule for them as may be done for the power that sustains, which is unique and determined.21
In fact, this is true for all of the machines, for while the conditions for equilibrium in each case are determinate and subject to an exact mathematical rule, the conditions for motion are many and indeterminate and thus in principle are unknowable with any precision.
According to Guidobaldo, Archimedes
Guidobaldo’s attempt to take into account the material resistance of real
machines comes up in several notes inspired by questions in the
Mechanica concerned with wheels. Question 11 of the
Mechanica asked why weights are more easily moved on rollers than on
wheels despite the fact that rollers are smaller in diameter than wheels; the
answer there was because wheels are subject to friction at the axel. Pietro
Catena
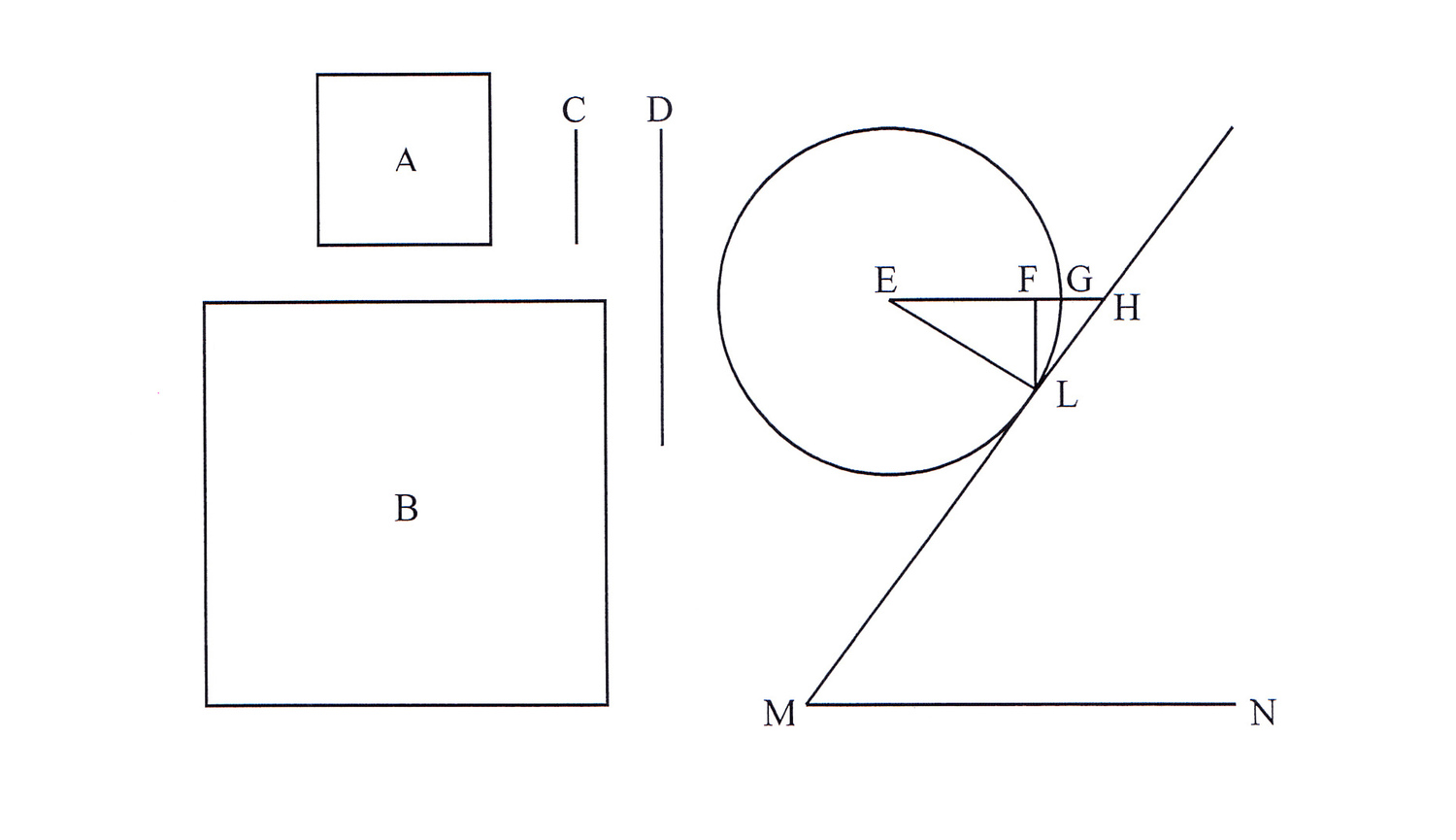
But in a variation of Question 9 of the Mechanica, Guidobaldo
attempted to take account of the friction of the axel mentioned in Question
11. He asks why weights are in practice more easily moved with larger wheels,
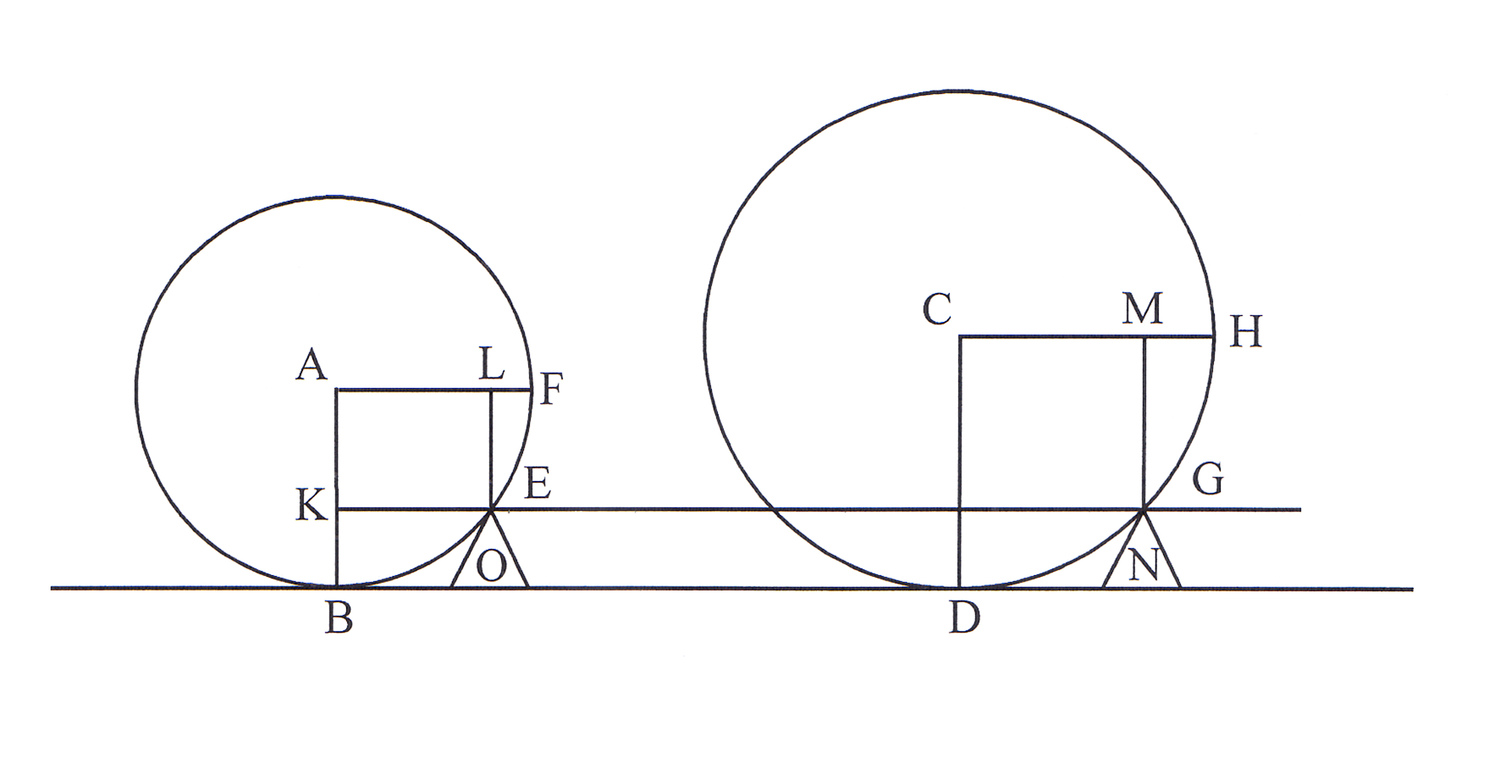
meaning in this case on a windlass. He imagines two equal weights suspended
from A and C on the circumferences of two unequal wheels concentric around
center G (see Figure 2.6). Since the weights at A and C are equal, the powers
needed to sustain them in equilibrium at D and B will also be equal. But to
move the weights, additional power must be added at D and B, since the axel
resists motion because of contact and friction, which Guidobaldo represents as
a load applied at E. Since the ratio of BG to FG is greater than the ratio of
DG to FG, less power must be added at B to overcome this resistance than at D.
Thus weights are moved more easily with larger wheels.27
These fragments are apparently all that he wrote, or all that survive, in his
attempt to reduce the pseudo-Aristotelian Mechanica to Archimedean
principles, and they are, at best, a mixed success. But they show several
important features of his approach to mechanics: they show his general
determination to bring mechanical effects under Archimedean principles (though
on occasion he resorted to motion and speed), and they show how he tried to
take into account the material resistance of real machines. And
the material resistance of real machines lies at the heart of Guidobaldo’s
attempt to exclude motion from the causes and principles of mechanics. A
letter he wrote to the mathematician Giacomo Contarini
where one must consider that the resistance that the material makes is made when weights are to be moved and not when they are merely to be sustained, because then the machine neither moves nor turns.28
Because resistance arises only when there is motion, according to Guidobaldo,
a balance in equilibrium corresponds exactly to abstract mathematical theory;
but to disturb that balance, to set it into motion, is to introduce all the
irregularities and uncertainties of matter. And working machines are precisely
such disturbed equilibria.29
Guidobaldo’s main contribution to the renaissance of mechanics in the
sixteenth century was to take the vague and wide-ranging scope of mechanics
suggested by the pseudo-Aristotelian Mechanica and restrict it to
Archimedean explanations of Heron’s
References
Bertoloni Meli, D. (1992). Guidobaldo dal Monte and the Archimedean Revival. Nuncius 7: 3-34
- (2006). Thinking with Objects. The Transformation of Mechanics in the Seventeenth Century. Baltimore: John Hopkins University Press.
Catena, P. (1556). Universa loca in Logicam Aristotelis in mathematicas disciplinas. Venezia: F. Marcolini.
Cohen, M. R., I. E. Drabkin (1958). Source Book in Greek Science. Cambridge: Harvard University Press.
De Gandt, F. (1986). Les mécaniques attribuées à Aristote et le renouveau de la science des machines au XVIe siècle. Les études philosophiques 3: 391-405
- (1987). L'analyse de la percussion chez Galilée et Torricelli. In: L'Œuvre de Torricelli: Science galiléenne et nouvelle géometrie Ed. by F. De Gandt. Nice: Les Belles Lettres 53-77
Drabkin, I. E., S. Drake (1960). Galileo Galilei On Motion and On Mechanics. Madison: University of Wisconsin Press.
Drake, S., I. E. Drabkin (1969). Mechanics in Sixteenth-Century Italy. Madison: University of Wisconsin Press.
Duhem, P. (1905-1906). Les origines de la statique. Paris: Hermann.
- (1991). The Origins of Statics. Dordrecht: Kluwer.
Favaro, A. (1899-1900). Due lettere inedite di Guidobaldo del Monte a Giacomo Contarini. Atti del Reale Istituto Veneto di Scienze, Lettere ed Arti 59, Part 2: 303-312
Frank, M. (2007). Das erste Buch der In duos Archimedis aequeponderantium libros paraphrasis von Guidobaldo dal Monte. München: Schriftliche Hausarbeit, Ludwig-Maximilians-Universität.
Galilei, G. (2002). Le mecaniche. Firenze: Olschki.
Gamba, E. (1998). Guidobaldo dal Monte, matematico e ingegnere. In: Giambattista Aleotti e gli ingegneri del Rinascimento Ed. by A. Fiocca. Firenze: Olschki 341-351
Gamba, E., V. Montebelli (1988). Le scienze a Urbino nel tardo Rinascimento. Urbino: QuattroVenti.
Henninger-Voss, M. (2000). Working Machines and Noble Mechanics: Guidobaldo del Monte and the Translation of Knowledge. Isis 91: 233-259
Keller, A. G. (1976). Mathematicians, Mechanics and Experimental Machines in Northern Italy in the Sixteenth Century. In: The Emergence of Science in Western Europe Ed. by M. Crosland. New York: Science History Publications 15-34
Laird, W. R. (1986). The Scope of Renaissance Mechanics. Osiris 2, s. II: 43-68
- (1991). Patronage of Mechanics and Theories of Impact in Sixteenth-Century Italy. In: Patronage and Institutions: Science, Technology, and Medicine at the European Court, 1500-1750 Ed. by B. T. Moran. Woodbridge, Suffolk: Boydell-Brewer 51-66
- (2000). The Unfinished Mechanics of Giuseppe Moletti. Toronto: University of Toronto Press.
- (in press). Francesco Maurolico and the Renaissance of Mechanics. In: Archimede e le sue fortune R. Moscheo and V. Fera
Maurolico, F. (1613). Problemata mechanica. Messina: Brea.
Micheli, G. (1992). Guidobaldo del Monte e la Meccanica. In: La matematizzazione dell'universo Ed. by L. Conti. Assisi: Edizione Porziuncola 87-104
Monte, Guidobaldo del (1577). Mechanicorum liber. Pesaro: Hieronymum Concordiam.
- (1581). Le mechaniche dell'illustriss. sig. Guido Ubaldo de' Marchesi del Monte: Tradotte in volgare dal sig. Filippo Pigafetta. Venezia: Francesco di Franceschi Sanese.
- (1588). In duos Archimedis aequeponderantium libros paraphrasis scholijs illustrata. Pesaro: Hieronymum Concordiam.
Montebelli, V. (1988). Il problema dell'equilibrio della bilancia nella polemica di Guidobaldo dal Monte con il `Goto'. In: Le scienze a Urbino nel tardo Rinascimento Ed. by E. Gamba, V. Montebelli. Urbino: QuattroVenti 213-259
Moody, E., M. Clagett (1952). The Medieval Science of Weights (Scientia de Ponderibus). Madison: University of Wisconsin Press.
Nemorarius, J. (1533). Liber de ponderibus. Nürnberg: Petrus Apianus.
- (1565). Jordani opusculum de ponderositate Nicolai Tartaleae studio correctum. Venezia: Curtius Troianus.
Rose, P. L. (1975). The Italian Renaissance of Mathematics. Genève: Droz.
Rose, P. L., S. Drake (1971). The Pseudo-Aristotelian Questions of Mechanics in Renaissance Cultures. Studies in the Renaissance 18: 65-104
Roux, S. (2010). Quelles mathématiques pour la force de percussion?. In: Ma- thématiques et connaissance du monde réel avant Galilée Ed. by S. Rommevaux. Montreuil: Omniscience 243-285
Tartaglia, N. (1546). Quesiti et inventioni diverse. Venezia: Venturino Ruffinelli.
Tassora, R. (2001) Le Meditatiunculae de Rebus Mathematicis di Guidobaldo del Monte. Ph. D. thesis. Università di Bari
Tucci, R. (2004) Il De momentis aequalibus di Francesco Maurolico: una proposta di ricostruzione della sua stratificazione testuale. Tesi di Laurea. Università di Pisa
Van Dyck, M. (2006). Gravitating Towards Stability: Guidobaldo's Aristotelian-Archimedean Synthesis. History of Science 44: 373-407
Footnotes
“Ac si aliquando, vel sine demonstrationibus geometricis, vel sine vero motu res mechanicae considerari possint” (Monte 1577, f. **1v; tr. Drake and Drabkin 1969, 245).
See (Duhem 1905-1906, I, 209–226; tr. Duhem 1991, 148–159). The phrases quoted are on p. 151 and 159.
Paris, Bibliothèque Nationale, fonds lat. ms 10246. See (Drake and Drabkin 1969, 48). The Meditatiunculae has been edited by Roberta Tassora (2001), a partial copy of which Pier Daniele Napolitani, who directed the thesis, kindly made available to me after this paper was written; the passages quoted from the Meditatiunculae are in my own transcriptions. The mechanical pages of the Meditatiunculae are discussed by Tassora (2001, 75–100).
On the sixteenth-century tradition of the Mechanica, see (Rose 1975; Rose and Drake 1971; De Gandt 1986; Laird 1986).
See (Nemorarius 1533 and 1565).
For Jordanus and the medieval science of weights, see (Moody and Clagett 1952; Tartaglia 1546; excerpts tr. Drake and Drabkin 1969, 104–143).
See (Maurolico 1613; Tucci 2004), on Maurolico’s mechanics, see (Laird in press).
On Commandino’s edition and translation of Pappus’s Mathematical Collection, and Guidobaldo’s role in its publication, see (Rose 1975, 209–213).
See (Monte 1577; tr. Monte 1581; tr. Drake and Drabkin 1969, 267–268).
“Eruditissimus tamen libellus de aequeponderantibus prae manibus hominum adhuc versatur, in quo tanquam in copiosissima poenu omnia fere mechanica dogmata reposita mihi videntur” (Monte 1577, f. **1r; tr. Drake and Drabkin 1969, 244).
“Tota mechanica facultas tanquam unico, praecipuoque fundamento innititur” (Monte 1588, 4); the Preface is edited and translated into German in (Frank 2007), the quotation is on p. 118; the translation quoted here is by Rose (1975, 234).
See (Monte 1577, ff. 30v–36r; tr. Monte 1581, ff. 29v–33v; tr. Drake and Drabkin 1969, 296, proofs omitted).
“Percioche lo spatio della possanza allo spatio del peso ha la medesima proportione, che il peso alla possanza, che sostiene il detto peso. Ma la possanza, che sostiene è minore della possanza che move, però haurà proportione minore alla possanza che lo move, che alla possanza, che lo sostiene. Lo spatio dunque della possanza che move allo spatio del peso haurà proportione maggiore, che il peso all’istessa possanza.” See (Monte 1577, f. 43r–v; tr. Monte 1581, f. 39v; tr. Drake and Drabkin 1969, 300).
See (Monte 1577); De trochlea, Prop. 28, Cor. 2, f. 107 v; tr. (Monte 1581, 101 v; tr. Drake and Drabkin 1969, 317); De axe in peritrochio, Prop. I, Corollary [3], f. 110r; tr. (Monte 1581, f. 106 r; tr. Drake and Drabkin 1969, 319); De cochlea, Prop. 2, Corollary, f. 128 r; tr. (Monte 1581, f. 125 r; tr. Drake and Drabkin 1969, 326).
For Galileo’s statement of the principle, see (Galilei 2002, 45–47); tr. (Drabkin and Drake 1960, 147–149).
Guidobaldo, Mechanicorum liber, De cuneo, f. 115 r, tr. (Monte 1581, f. 110 r; tr. Drake and Drabkin 1969, 321); De cochlea, [Prop. 2], ff. 126 r–127 r; tr. (Monte 1581, ff. 121 r–122 r; tr. Drake and Drabkin 1969, 325–326).
See (Monte 1581, ff. 121 r–v; tr. in part in Drake and Drabkin 1969, 325–326); as Bertoloni Meli pointed out (Bertoloni Meli 1992, 25, note 42), Drake’s translation mistakenly prints H instead of G throughout; Pappus’s full proof can be found in translation in (Cohen and Drabkin 1958, 194–196); a discussion of Guidobaldo’s use of Pappus’s proof can be found in (Bertoloni Meli 2006, 35–37).
The proof is as follows: “Ducatur GH horizonti equidistans, cui ad rectos angulos ducatur CH, DK, sitque in hoc circulo constituenda potentia spheram sustinens in G. Sphera vero secetur per centrum et per C, plano horizonti erecto, quod quidem in sphera circulum efficiat maximum ABC. Sphera enim ABD habeat centrum D, que subiectum planum EF horizonti inclinatum in C contingat. Potentia invenire que datam spheram subjectum planum horizonti inclinatum tangentem in dato puncto sustineat. Oportet vero potentiam ita in sphera constituere ut circulus maximus per potentiam, et tactum transiens sit horizonti erectus. Intelligatur itaque GH vectis, cuius fulcimentum est in H, cum planum EF spheram tangat in C. Pondus vero in K esset appensum. Cum enim D sit centrum gravitatis sphere, erit perinde, ac si in K esset appensum ex dictis in tractatu de vecte nostrorum mechanicorum. Quam vero proportionem habet GH ad HK, ita fiat gravitas sphere ad potentiam in G. Potentia igitur in G cognita erit. Ac in prima quidem figura erit primus modus vecte, in secunda secundus, in tertia tertius. Notandum tamen quod si potentia esset in G, ita ut ducta horizonti perpendicularis per centrum sphere D transiret, ut DG tunc potentia totam sustineret spheram ac propterea ipsi equalis existeret. Veluti in puncto quoque B ob eandem causam” (Guidobaldo del Monte, Meditatiunculae de rebus mathematicis, Paris, BNF, fonds lat. ms 10246, 64; see Tassora 2001, 302–303).
See (Monte 1577, f. 118 v–119 r; tr. Monte 1581, f. 114 r–v; tr. Drake and Drabkin 1969, 322–323); on the force of percussion, see (De Gandt 1987; Laird 1991; Roux 2010).
“Percioche essendo, che le possanze lo quali movono possano essere infinite, non sene puo assegnare ferma regola, come si farebbe della possanza, che sostiene, laquale è una sola e determinata.” See (Monte 1581, f. 127 v; tr. Drake and Drabkin 1969, 328); the insertion is mine.
See (Monte 1588, 4; Frank 2007, 118; see Rose 1975, 234).
Del Monte, Meditatiunculae, 30; see (Tassora 2001, 266).
Del Monte, Meditatiunculae, 31–32; see (Tassora 2001, 267–268).
Del Monte, Meditatiunculae, 55–56; see (Tassora 2001, 292–293); a similar proof is given by Giuseppe Moletti in his unpublished Dialogue on Mechanics of 1576, for an edition and English translation of which see (Laird 2000, 97–99).
See (Catena 1556, 81–83; del Monte, Meditatiunculae, cit., 60–61; Tassora 2001, 298–300); that Guidobaldo heard Catena’s lectures, see (Rose 1975, 222).
Del Monte, Meditatiunculae, 59; see (Tassora 2001, 297–298).
“dove è da considerare che la resistanza che fa la materia lo fa quando si hanno da mover i pesi e non quando se hanno da sostenere solamente, perché all’hora l’instrumento non si move né gira.” Guidobaldo del Monte to Giacomo Contarini, Pesaro, 9 October and 18 December 1580, ed. Antonio Favaro (1899-1900); quoted in part in (Gamba and Montebelli 1988, 75–76); for the letter to Pigafetta, see (Keller 1976, 28).
On this point see (Van Dyck 2006, 398–399).
See, for example, his notes on bodies falling through resisting media (Guidobaldo, Meditatiunculae, 41–42) and on the path of projectiles (op. cit., p. 236); see also (Tassora 2001, 90–93, 181–186, 281–283, 545–547).