Chapter structure
- 3.1 Introduction
- 3.2 The Incipit of Benedetti’s De mechanicis
- 3.3 Del Monte’s Rebuttal of the Negligibility of the World’s Center
- 3.4 Benedetti’s Generalization: From Weights to Forces
- 3.5 Del Monte’s Misunderstanding
- 3.6 On Tartaglia: Diverging Approaches
- 3.7 Conclusions: The Triangulation Benedetti-del Monte-Galileo
- 3.8 Appendix 1: Benedetti’s De Mechanicis, Chapters I–III
- 3.9 Appendix 2: Del Monte’s Meditatiunculae, ff. 145 and 146
- References
- Footnotes
3.1 Introduction
Guidobaldo del Monte’s handwritten notes on scientific and technical matters Meditatiunculae de rebus mathematicis contain, among other things, a criticism of the basic principles of mechanics set down by Giovan Battista Benedetti in De Mechanicis. This was printed as the third section of his book Diversarum speculationum mathematicarum et physicarum liber (Turin, 1585). Both Benedetti and del Monte are central figures in the history of sixteenth-century science: Benedetti provided an important source for understanding the struggles of early modern engineer-scientists with the ancient heritage of mechanical knowledge from Aristotle
Let us briefly recapitulate the biographies of the two protagonists of this controversy. Guidobaldo del Monte was born on 11 January 1545 in Pesaro in the territories of the Duke of Urbino. He was taught mathematics by Federico Commandino, who also instilled in him a love of the classics, especially Archimedes
The second protagonist of our controversy, Giovanni Battista Benedetti was born in Venice on 14 August 1530. He was first educated by his father and, according to a brief autobiographical remark of Benedetti, later studied the first four books of Euclid’s
A recent analysis of the Renaissance controversies on equilibrium centers on the edition of the marginal notes that del Monte made in his personal copy of Benedetti’s book (Renn and Damerow 2012)
3.2 The Incipit of Benedetti’s De mechanicis
Benedetti’s book on mechanics begins with a brief introduction that is significant in that it reveals a strong “modernist commitment.” The author is convinced that the advancement of science is a future-oriented process in which novelty plays a crucial role. As a scholar of mechanics, he acknowledges to owe much to the work of past generations (scripserunt multi multa). Yet, he maintains that nature and practice (natura ususque) always bring to light something previously unknown. Accordingly, he promises to provide those interested in mechanical problems (his qui in hisce mechanicis versantur) with new insights or, in his words, “things that have never been tried nor explained with sufficient accuracy before” (Benedetti 1585, 141). The importance that he attaches to his treatise De mechanicis is evidenced by his hope and expectation that future generations would remember him for his scientific achievements in the field of mechanics. Before dealing with the foundational principles of mechanics, Benedetti stresses the unprecedented originality of his contributions but makes no explicit reference to any forerunners or contemporary scholars. Del Monte, who had published his Mechanicorum liber only a few years earlier, would undoubtedly have been offended by this omission. In addition, Benedetti’s “progressivist” conception of scientific research potentially contrasted the past-oriented idea of knowledge as a restoration that prevailed during the Renaissance. This aspect could also mark a profound disagreement between his own and del Monte’s (and the Commandino school’s) purist understanding of science as a restoration of classical sources through accurate philological and mathematical work in the wake of Archimedes.
3.2.1 Pondus and Gravitas
The first section of Benedetti’s De mechanicis presents the basic thesis that the weight of a body placed at the extremity of a balance varies in relation to the different inclinations of the beam. This idea goes back to the medieval scientia de ponderibus and, in particular, to the work of Jordanus Nemorarius
The essentialist meaning Benedetti attaches to the term pondus can be traced back to an implicit scholastic background: pondus is a “substance” (in the Aristotelian meaning of hypokeimenon) while gravitas is its “accidental” property, which can be increased or diminished without affecting the essence. In other words, we are confronted with an Aristotelian treatment of quantity (in this case the gravitas) as the propriety of an entity (in this case the pondus), whose degree of heaviness varies in a qualitative manner.
The profound relation of Benedetti’s conception with scholastic Aristotelianism emerges even more clearly when one considers that the concept of gravitas secundum situm from which his conception derives was itself shaped by Aristotelian logic. More specifically, the concept of gravitas secundum situm can be understood as having been introduced in thirteenth-century mechanics to avoid fallacies that could arise without such a differentiation and specification of the concept of weight.
Aristotle
The analogy with the concept of gravitas secundum situm is evident: according to the doctrine of positional heaviness, weight must be considered in a particular respect, that is, in dependence of its collocation. Just as a general concept has sometimes to be subjected to a restriction of its meaning (diminutio) by considering it secundum quid before any conclusions can be drawn, so the concept of weight has also to be specified with regard to its collocation before reaching any conclusions, for example, about the equilibrium of a balance.
It should be remarked that according to scholastic logic the determination of heaviness secundum situm does not allow conclusions to be made about the absolute weight of a body. The acknowledgment of the relativity of weight, depending on the specification, would eventually undermine Aristotelian natural philosophy on the basis of considerations derived from Aristotelian logic. Benedetti for instance, connected the relativity of heaviness not only to positional heaviness, but also to the medium in which a body is submerged and moves. In the fourth book of Diversae speculationes, entitled Disputationes de quibusdam placitis Aristotelis, he famously based his treatment of the motion and the fall of bodies through a medium on Archimedean hydrostatics. This theoretical background permitted him (as later Galileo) to relativize heavy and light, depending on the density of the medium. Moreover, he considered the resistance of the medium as a factor to be taken into account in dynamics and thereby reassessed the existence, and even the necessity, of void in nature. Paradoxically, Benedetti (and later Galileo
3.2.2 De mechanicis, Chapter I: “On the different positions of the beams of a balance”
In chapter I, Benedetti notes that “a body (pondus) [...] acquires a larger or smaller weight (gravitas) depending on the different ratio of the beam’s position” (pondus [...] maiorem, aut minorem gravitatem habet, pro diversa ratione situs ipsius brachii). According to Benedetti, a body has the greatest heaviness when the beam at whose extremity it is loaded is in the horizontal position. His idea is based on a simple common-sense intuition: if one considers an equal-arms balance suspended at its center, the weight of a loaded body:
is borne entirely by the fulcrum when resting vertically upon it,
is entirely hanging on the fulcrum when suspended vertically below it,
is not supported in any way by the fulcrum when the beam is in the horizontal position.
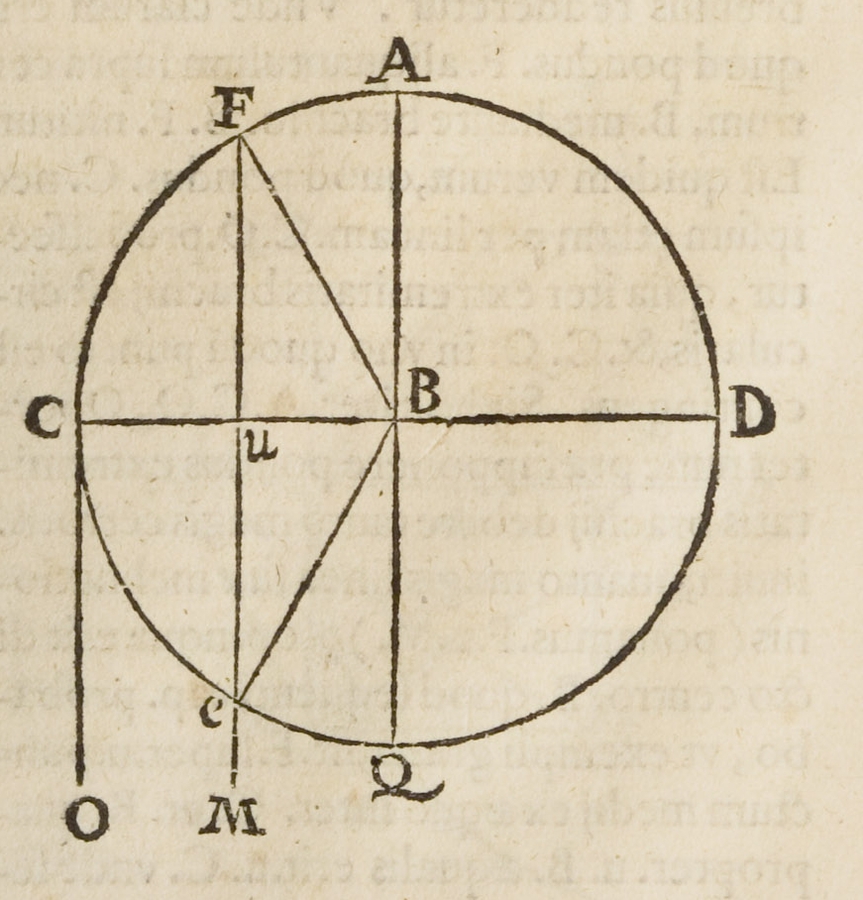
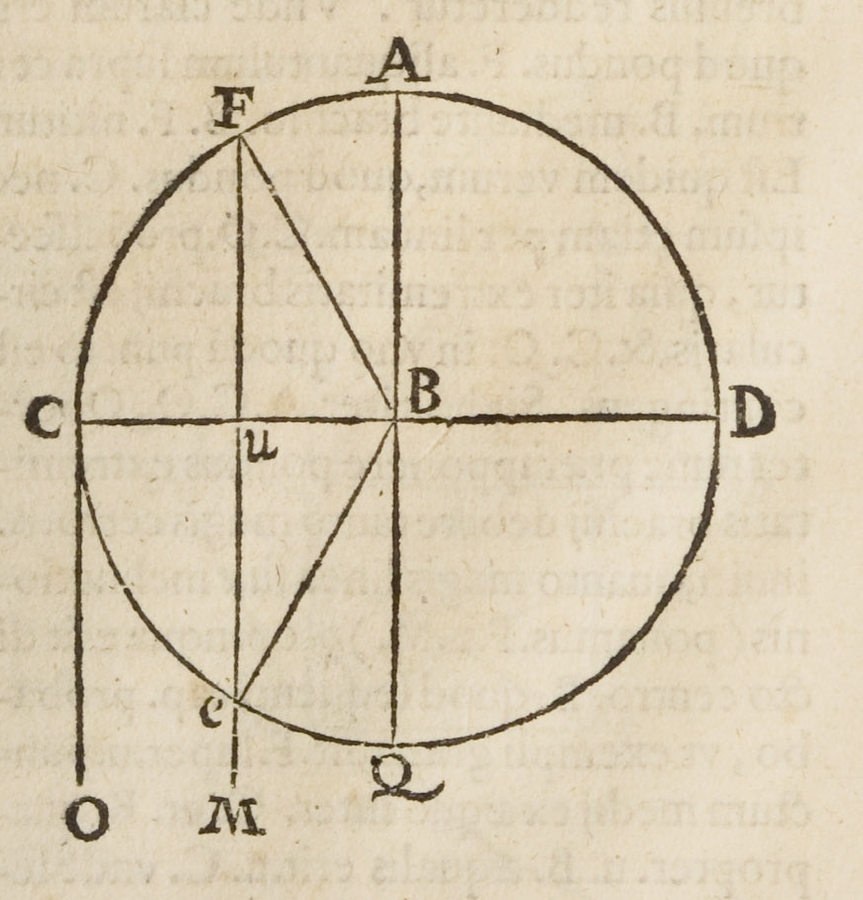
Fig. 3.1: Figure in Benedetti’s De mechanicis, Chapters I and II.
In the first case, the body completely rests or leans on the center (nititur), and the center in turn hinders (impellet) the downward tendency of the weight. In the second case, the body is suspended vertically (pendet) and the center “attracts” it (attrahet), in the sense that it hinders its natural tendency to fall down (inclinatio). Hence, the body attains its maximum weight in the third case. If the beam of a balance moves upward, departing from the horizontal position, the weight slowly decreases and reaches its minimum at the top when the beam is in the vertical position. If the rotatory motion around the fulcrum continues, now downward, the weight increases again until it reaches its maximum in the horizontal position. It then diminishes until it is suspended entirely below the fulcrum. Benedetti visualizes these variations of weight in dependence on the position (situs) thanks to a diagram comparing the lines connecting the weight to the center of the world in different cases, and precisely if the beam:
is horizontal,
is raised upward, or
(which is equivalent to the second case) is moved downward with the same angle as in the second case.
The parallel lines, called lineae inclinationis or lineae itineris, indicate the direction in which a body would fall if it were free. The closer these lines are to the center of the beam, Benedetti says, the “less heavy” the body becomes (Figure 3.1).
In his copy of Benedetti’s book, del Monte wrote a brief annotation in the margin of chapter one: “this first chapter is derived entirely from our treatise on the balance in the Mechanicorum liber.”5 Clearly, he vindicated the relevance of his treatise for Benedetti’s speculations, in spite of the latter’s claims of originality. It should be remarked, however, that del Monte’s treatment of the balance, based on the concept of center of gravity, was significantly different from Benedetti’s, which was based on an original reworking of positional heaviness. For del Monte though, he merely reassessed a concept received from authors such as Jordanus Nemorarius
3.2.3 De mechanicis, Chapter II: On the proportion of weights at the extremities of a balance beam in a position other than the horizontal
In chapter II, Benedetti deals with the proportions of a weight placed at the extremity of a balance beam if its position is not horizontal (De proportione ponderis extremitatis brachii librae in diverso situ ab orizontalis). The thesis to be demonstrated is the following: “The proportion between [the weight of] a body (pondus) at C and [the weight of] the same body (pondus) at F corresponds to that between the whole beam BC and its part BU which is [set on the beam BC and is] delimitated by the fulcrum and the [intersection between the beam and the] inclination line FUM that connects the weight at F to the center of the world” (Benedetti 1585, 142. Figure 3.2).
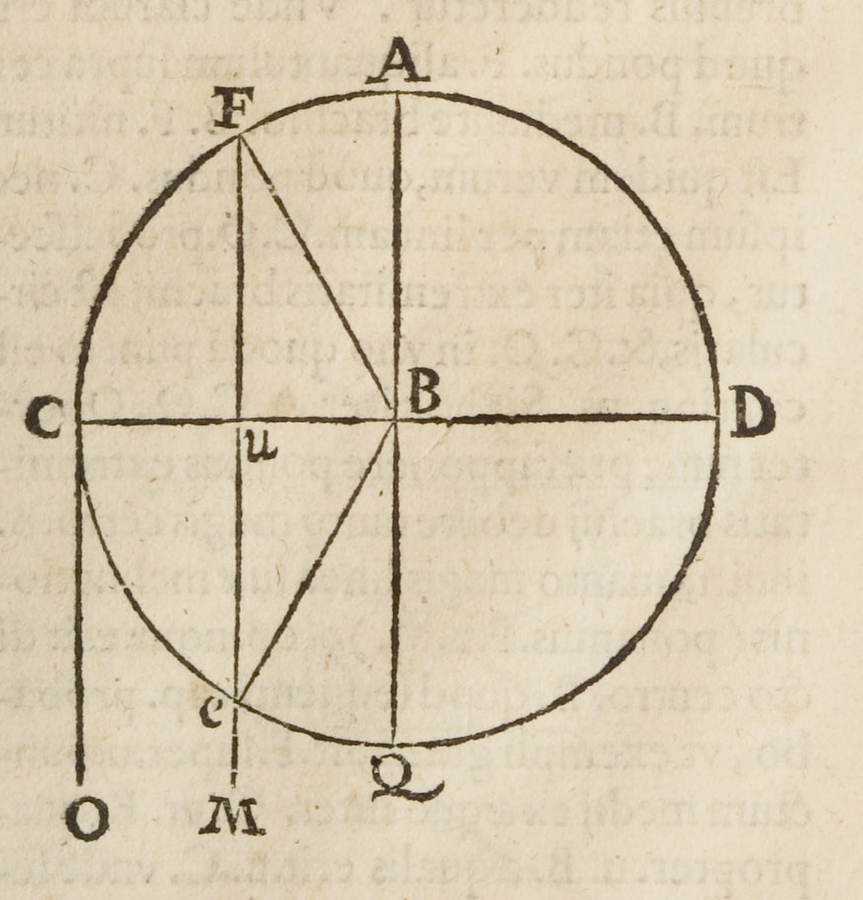
Fig. 3.2: Benedetti discusses in De mechanicis, chapter II, the same figure as in De mechanicis, chapter I.
For the sake of simplicity, we represent these relations symbolically, in modern terms:
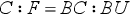
|
where C is the weight in the horizontal position and F in the inclined position; BC is the beam and BU the part of the beam BC between the center B and the perpendicular line drawn from F.
Benedetti’s demonstration is as follows. He imagines placing a weight D on the other extremity of the balance that has the same proportion to C as F, that is, the following proportion expressed in modern terms:
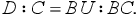
|
In accordance with Archimedes’s
The next step is to show that F : C = BF : BU (where BF is the beam, hence BF = BC). In order to demonstrate this, Benedetti resorts to the mental model (imaginemur) of a string hanging vertically from F to which a weight equal to C is suspended. He claims that it is visually evident that the weight has the same effect at F as at U. The same is valid for the case in which the weight is suspended from U and intersects the circumference described by the rotation of the beam at a point E. In both cases, the balance would remain horizontal since the weight C at F, U or E would balance the weight at D. Benedetti further argues that the balance under consideration can be treated like a bent lever with a horizontal and an inclined arm (FBD or EBD): “si brachium BE consolidatum fuisset [...]” (If the beam BE was made solid [...]).
The author concluded that his reasoning has satisfactorily demonstrated his thesis: “A body (pondus) is more or less heavy (grave) the more or less it hangs from (pendet) or rests on (nititur) the fulcrum” (Benedetti 1585, 142). And he deems this resting on or hanging from the fulcrum to be the most direct cause (haec est causa proxima, et per se) of the positional changing of a weight.
As an additional commentary, Benedetti remarks that in his diagram he supposes the inclination line CO to be perpendicular to CB and parallel to BQ, whereas CO and BQ in fact converge at the center of the sphere of the elements (centrum regionis elementaris), that is, the Earth. But for the sake of his present argumentation, this angle is negligible and one may remain with the assumed perpendicularity and parallelism. Benedetti thus developed a method to quantify positional heaviness that corresponds to the modern concept of “torque.”
3.3 Del Monte’s Rebuttal of the Negligibility of the World’s Center
As will be shown in the following, only in his initial treatment of the inclined balance did Benedetti neglect to consider the convergence of the inclination lines to the center of the elements, that is, in chapter one of De mechanicis. This omission gave rise to criticism in the Meditatiunculae by del Monte, who, to dispel Benedetti’s reasoning in De mechanicis, chapter I, did not accept his premises. Rather, he assessed Benedetti’s arguments from his perspective, relying on the idea of center of gravity as developed in his own book on mechanics.
A marginal note by del Monte documents his disagreement with Benedetti’s conclusion: “Thus, in this manner, a weight (pondus) more or less hangs from or rests on the center; this is the next cause and the [cause] in itself [of the variation in heaviness].”6 As a marginal note (Figure 3.3), he wrote:
because that [that is, the greater or smaller extent to which a weight rests at the center] is neither the next [cause] nor the [cause] in itself. For the weight at F of the arm BF is not equally heavy as the weight U of the arm BU; nor is the weight at E of the arm BE equally heavy as the weight at U of the arm BU. Thus, this entire demonstration is false.7

Fig. 3.3: Del Monte’s marginal note to De mechanicis, chapter II.
This means that del Monte did not accept the claim that a weight is equally heavy in different positions on the beam of the balance, provided the projections of the beam along the horizontal are the same length or rather, as Benedetti writes, the distances between the projections of the beam on the horizontal and the center have the same lengths.
To find del Monte’s counter-arguments, we shall look to the Meditatiunculae, f. 145, Contra Cap. 2 Jo. de Benedicti de Mechanicis. As mentioned, he basically rejected Benedetti’s perspective by objecting that he did not take into due account the finite distance of the weights from the center of the world and hence the fact that the plumb lines are not parallel to each other, as Benedetti assumed in this part of his treatise.
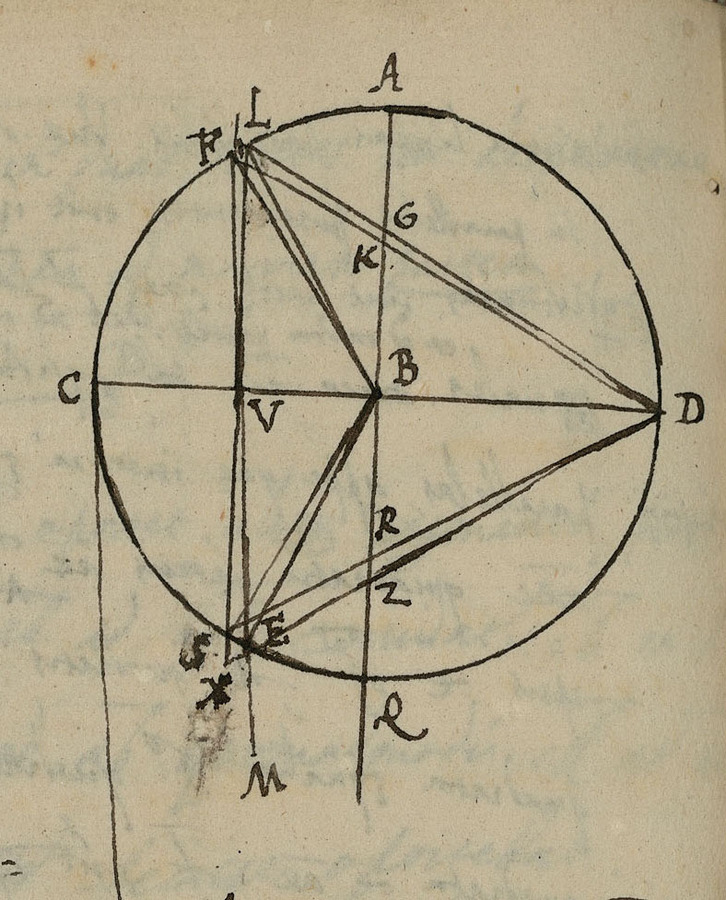
In his diagram (Figure 3.4), del Monte compared the line LUS parallel to the line AQ, connecting the fulcrum B of the balance with the center of the world M, with the line FM connecting the upper weight F and the lower weight E with the center of the world M. S is the point at which the line LUS meets the circle that the beam makes around the fulcrum, which is above the position of the lower weight E.
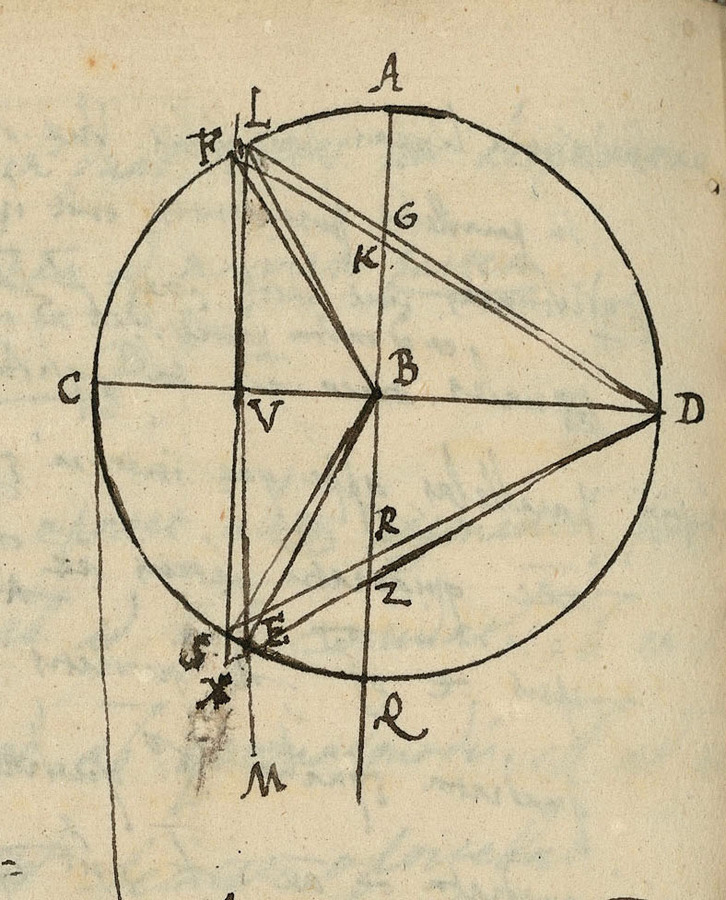
Fig. 3.4: Del Monte's reconsideration of Benedetti's analysis of the bent lever.
He next considered a bent lever made of the oblique arm BS, rigidly connected to the straight arm BS, assuming that BU is half BD. If a weight is now placed at S that is double the weight at D, the bent lever will be in equilibrium, as del Monte showed with reference to his book, because the center of gravity of the weights at S and at D will be at the point R, which will be in its lowest place on the vertical line BQ. He therefore concluded that it is the weight at S, but not the lower weight E, that will be equally heavy as the weight at U.
He proceeded to demonstrate this in greater detail by considering the proportions in which the line connecting the two weights is cut by the perpendicular BQ for the two cases, that is, the weight placed at S and the weight placed at E. Del Monte concluded that the same weight is heavier at S than at E. He then turned to a closer consideration of the upper weight F. Again he constructed a bent lever LBD in equilibrium in order to compare it with the bent lever formed with the upper weight F. Again he showed that the weight is heavier at L than at F.
Del Monte concluded by summarizing that the entire fallacy is due to Benedetti assuming that the weight at F would gravitate in the same way as at U, which would only be the case, according to del Monte, if it were to hang freely.
3.4 Benedetti’s Generalization: From Weights to Forces
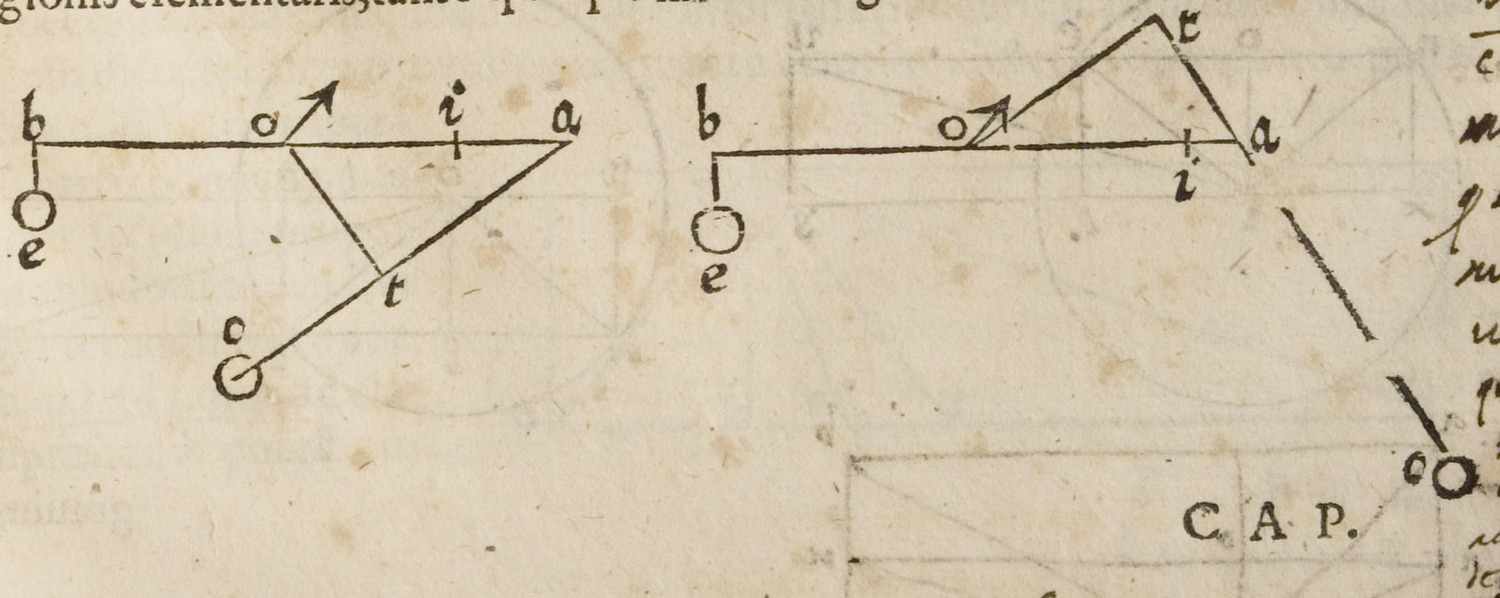
Chapter three of Benedetti’s De Mechanicis contains a generalization of the results of chapter two or, rather, presents a general rule concerning the action of forces (virtutes) on the beams of a balance, also in the case that they do not act vertically downward but also with an acute or obtuse angle (Figure 3.5). Benedetti resumes the result of the previous chapter as follows: the length of the line perpendicularly connecting the center to the line of inclination (the line BU in the diagram) allows the quantity of the positional force (quantitas virtutis [...] in [...] situ) of a weight (F in the diagram) to be established. Thus, Benedetti calls the positional weight a force and this is the presupposition to generalize from gravitas the action of what he calls virtutes moventes, or “moving forces.” The thesis of this chapter is summarized in its title: “That the quantity of any given weight (pondus) or moving force in relation to another quantity can be determined thanks to the perpendicular projections connecting the center of the balance to the line of inclination.”
Benedetti draws two diagrams showing a balance at whose extremities two weights or forces act in different directions. At the left extremity B, a weight E has a downward tendency while, at the right extremity, a weight C acts making an acute or an obtuse angle. According to Benedetti, the length of the perpendicular projection drawn from the center to the inclination line, OT, permits the determination of the distance OI on the beam at which the same force acting vertically downward produces the same effect. Given this equation, Benedetti can determine how much the force acting in a non-perpendicular direction has to be augmented in order to balance an equal weight acting perpendicularly on the opposite beam. This measure is given according to the following proportion (expressed in modern terms):
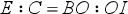
|
where E is the weight acting vertically on the extremity B; C is the virtus movens acting on the opposite extremity A with an angle; BO is the left beam and OI the part of the right beam OA determined as explained above.
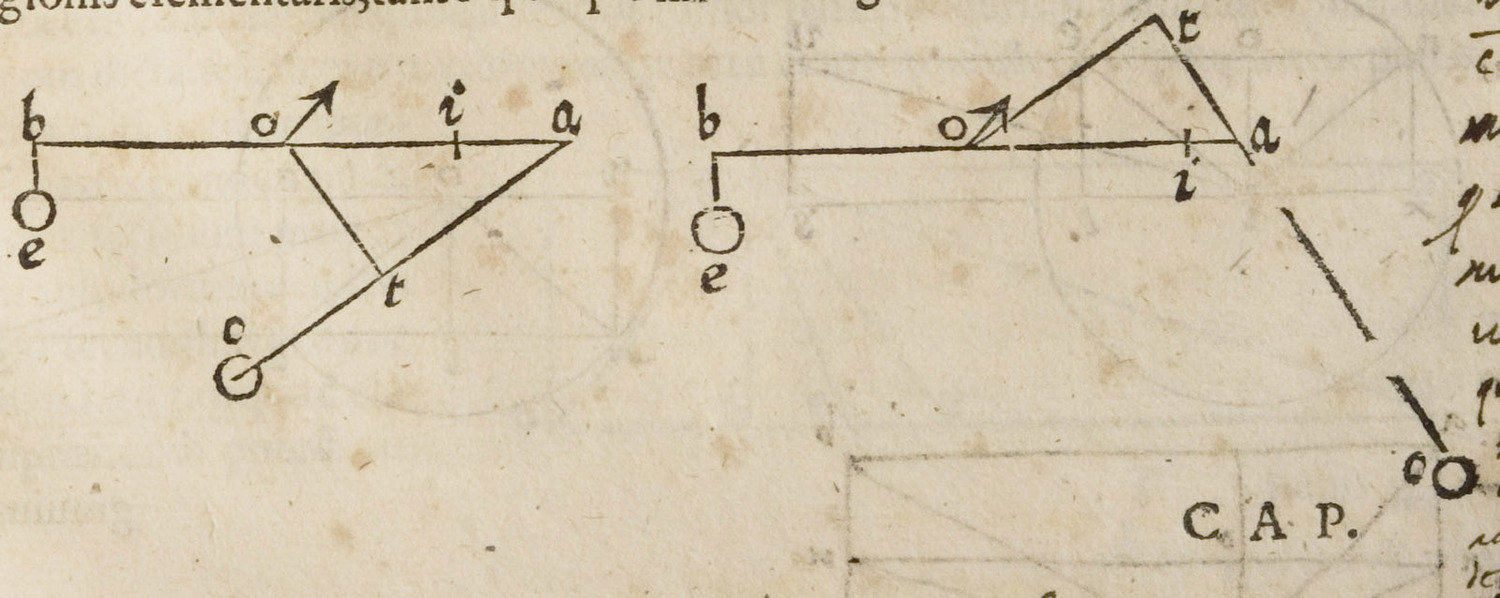
Fig. 3.5: Benedetti’s representation of forces acting on a balance in arbitrary directions.
In his argumentation, Benedetti thus equates a balance (BOI) with a bent lever (BOT). Accepting this equation, he concluded that, according to commonly shared knowledge (communi quadam scientia), the weights or forces that are required to obtain a perfect balance can easily be calculated.
The chapter ends with a cosmological corollary: “The closer the center O of the balance is to the center of the elementary sphere, the less heavy (minus grave) it becomes.” In fact, the angles between the beam and the inclination lines become progressively smaller.
3.5 Del Monte’s Misunderstanding
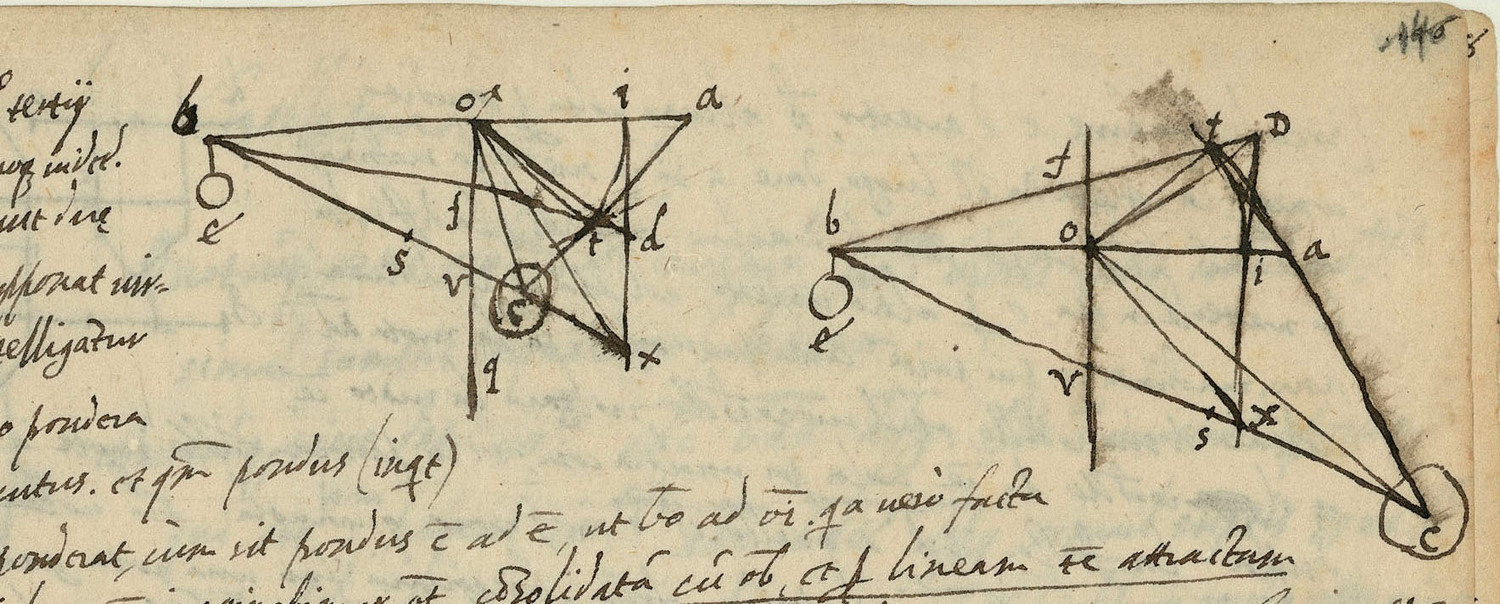
In his notes on folio 146 of the Meditatiunculae, del Monte grappled with Benedetti’s instructions of how to determine positional heaviness in the case of forces acting in an arbitrary direction. These he refuted at length under the erroneous assumption that Benedetti had claimed forces can be indiscriminately replaced by weights. Like Benedetti, del Monte considered a bent lever BOAC with fulcrum O, weights E and C, a straight arm BO and a bent arm OAC to discuss the two cases of an acute and an obtuse angle BAC (Figure 3.6).
He first recapitulated Benedetti’s procedure, assuming that a vertical line OT drawn from the fulcrum to the line AC represented the oblique arm of the bent lever. He stated that when the weight C is placed at the end of the horizontal line OI, whose length is the same as that of the perpendicular OT, according to Benedetti it will be in equilibrium with the weight E if the weight C is to the weight E as is BO to OT or OI. Del Monte then summarized Benedetti’s claim that when a force represented by the weight C acts along the line TC, the bent lever formed by the straight arm BO and the oblique arm OTC will also be in equilibrium, which he doubted.
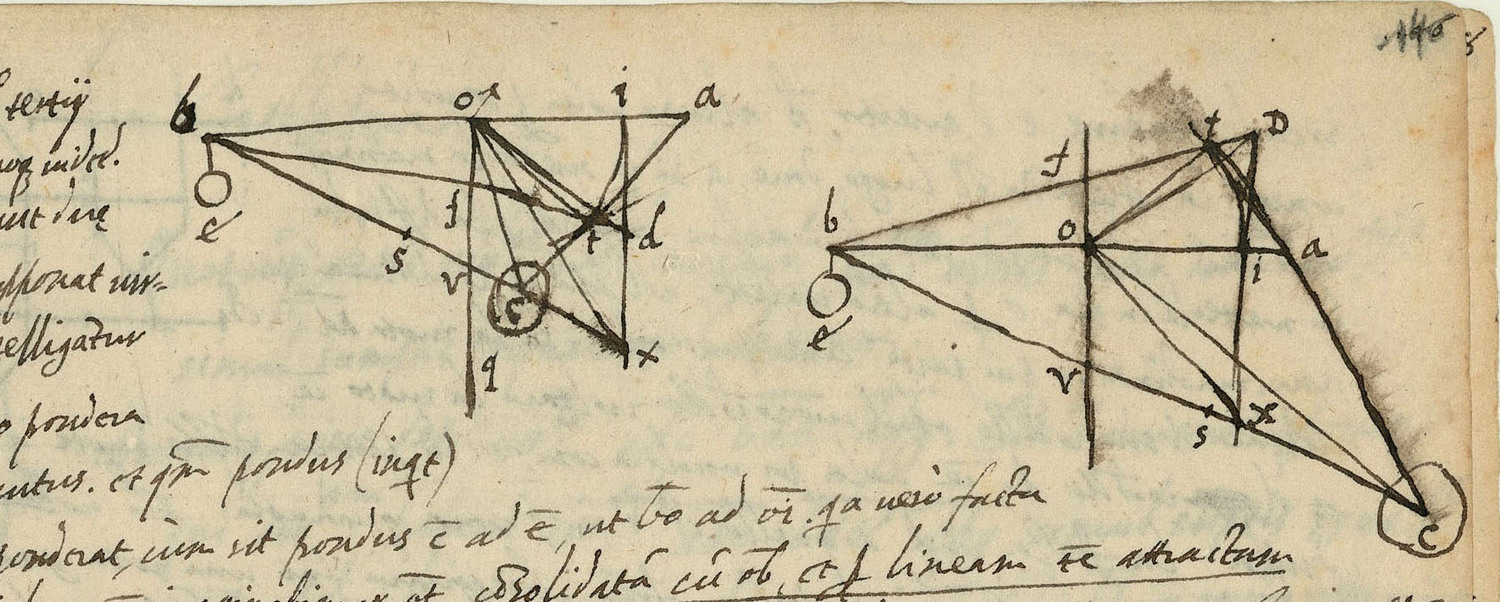
Fig. 3.6: Del Monte’s critical reworking of Benedetti’s representation of forces acting on a balance in arbitrary directions.
Del Monte reformulated this claim by stating that the same weight C will be in equilibrium with the weight E, whether it is placed on the straight balance BOI or on the broken bent lever BOTC. He thus replaced Benedetti’s conception of a force acting along an oblique line with that of a weight always tending downward and as a result arrived at absurd conclusions.
Del Monte then showed that the same weight will be heavier on the horizontal at point I than along the bent lever at T, demonstrating that the bent lever TOB will not be in equilibrium if the straight lever BOI is in equilibrium. To show this, del Monte again proceeded by finding the center of gravity of the weights E and C placed at T. More precisely, del Monte determined a position for the weight C where the bent lever is in equilibrium, a position, however, that is distinct from T. Thus it follows that T cannot be the position of equilibrium. For this purpose, he extended the line BT to D, just beneath I, so that it is immediately evident that if the weight C is placed at D, the center of gravity of the two weights will be just beneath the fulcrum.
Using the same pattern, he continued by showing that the bent lever BOC cannot be in equilibrium because its center of gravity S can never fall on the perpendicular line OU through the fulcrum. Finally, he applied this argument to the broken bent lever BOTC. Del Monte next addressed the case in which the bent lever is characterized by an obtuse angle BAC, showing that the weight at T is lighter than the weight at I. In his concluding remarks, however, he began to waver. Once again, he stated that Benedetti is completely mistaken when applying his procedure to weights. But he did admit that this may be true when dealing with a force.
As an afterthought, del Monte once again criticized Benedetti’s appeal to common sense: he did not feel this to be worthy of an expert mathematician. And as a second afterthought, he constructed an extreme case in which it is immediately clear that the broken bent lever cannot be in equilibrium if weights are attached to it rather than forces.
The following considerations enable del ’s marginal annotations to Benedetti’s De Mechanicis, chapter III, to be understood. These are not perfectly legible, but nonetheless their meaning becomes clear in light of the Meditatiunculae:
If we understand that a weight is at C, as we can assume from his own words, then CT must also be understood as being solid [and connected with] the solid lines TO […] If we hence understand that C is a weight and not moving, [the proposition] is false. If it is understood that C moves as […] of a man, it can be true, since what moves is not a weight. [But] if he himself assumes in the following that [this] can be demonstrated [also for a weight], nothing […] therefore as is evident in chapter 7. All demonstrations of the author are founded on these two chapters inasmuch as they are the first fundaments of mechanics; once their falsity is recognized, everything is rejected.8
3.6 On Tartaglia: Diverging Approaches
Del Monte’s and Benedetti’s criticisms of Tartaglia’s conception of positional heaviness help us to understand where these two scholars converge and diverge on the issue of the equilibrium (or lack of equilibrium) of a balance deflected from its horizontal position, and also the reasons for the presumed equilibrium or tendency to restore it. Moreover, their arguments reveal a different attitude toward the medieval tradition of the scientia de ponderibus and the gravitas secundum situm.
3.6.1 The Tradition of Jordanus, Tartaglia and Cardano
The concept of gravitas secundum situm, or positional heaviness, was extensively employed in Jordanus Nemorarius’s
In the sixteenth century, Tartaglia
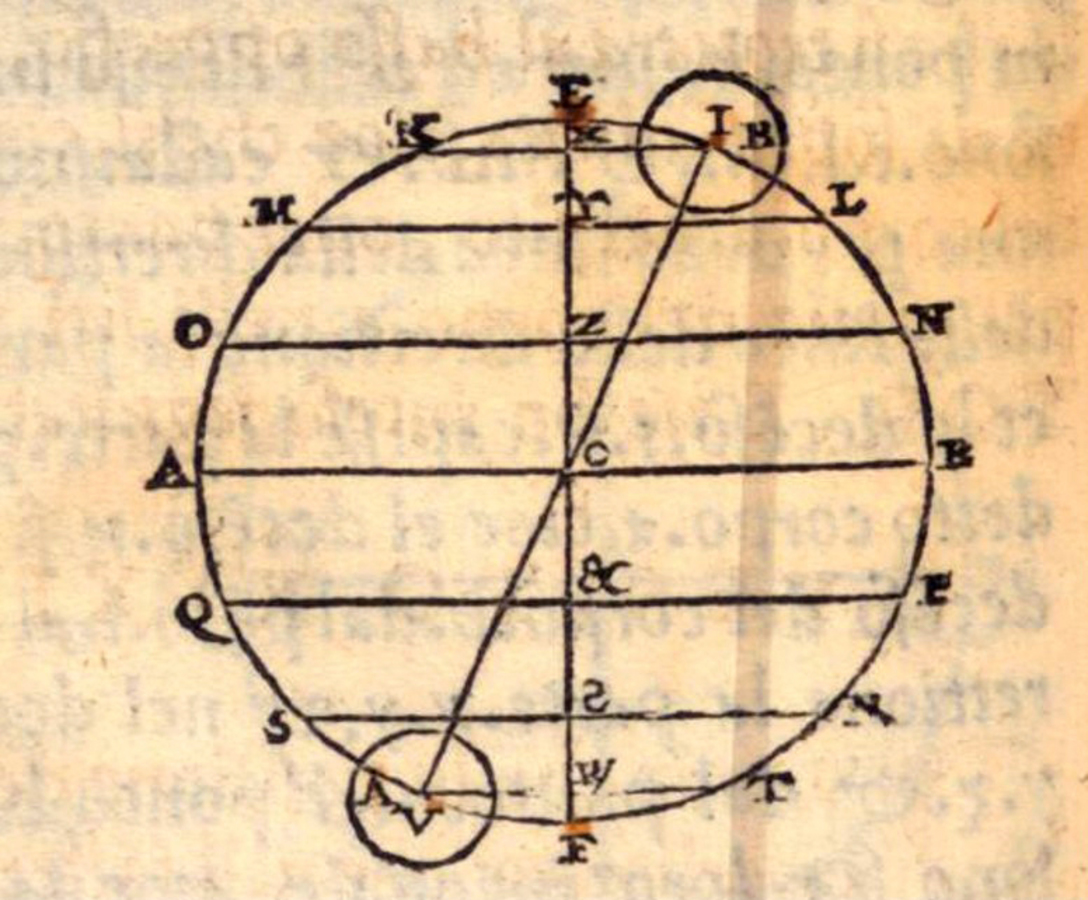
Fig. 3.7: According to Tartaglia
DESCENT: A first method of dealing with positional heaviness consisted in comparing the lengths of the projections of the equal arcs described by the motion of opposite balance beams—one ascending and one descending—on the vertical line of descent to the center of the world.
As Tartaglia’s diagram shows (Figure 3.7), the vertical component of decent of the upper weight is always larger than that of the lower. Thus, the former acquires more heaviness (secundum situm) than the latter and the balance returns to the horizontal position.
ANGLE OF CONTACT: Tartaglia’s
By comparing the angles of contact of the two weights, Tartaglia
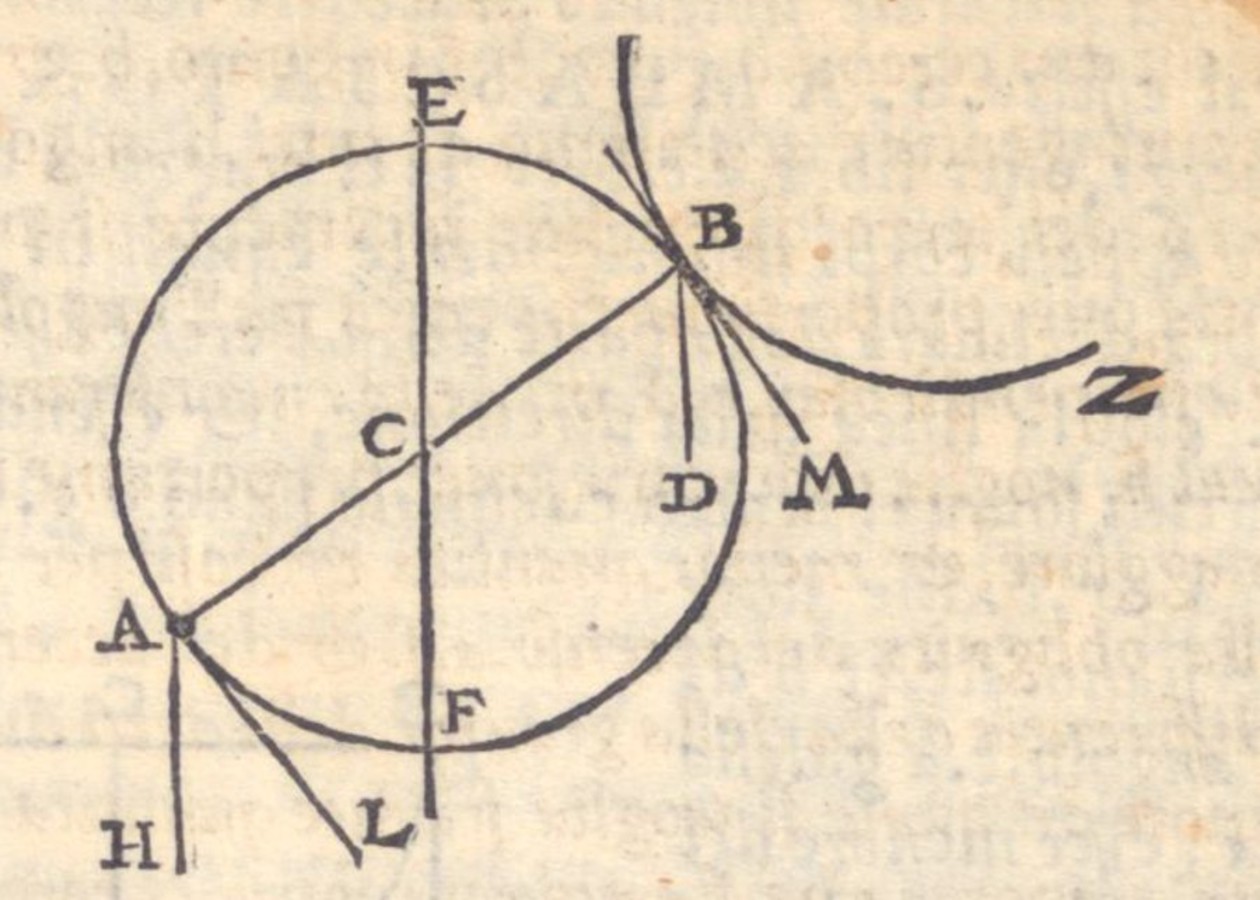
Fig. 3.8: According to Tartaglia, the body at B is positionally heavier than the body at A since the angle of contact between BD and the arc BF is smaller than the angle between AH and the arc AF.
THE ANGLE BETWEEN THE SUPPORT AND THE BEAMS: We have considered two ways of determining positional heaviness on the basis of Tartaglia’s
Aristotlesays that this happens when the support is above the balance, because the angle QBF of the meta is larger than the angle QBR. And similarly, when the support is QB, the meta will be AB, and thus the RBA will be larger than the angle FBA, but the larger angle will render the weight heavier. […] The general reason is hence this: the more the weights are removed from the meta or from the line of descent along a straight or an oblique line, that is, [as measured] by an angle, the heavier they are.10
Given these premises, Cardano
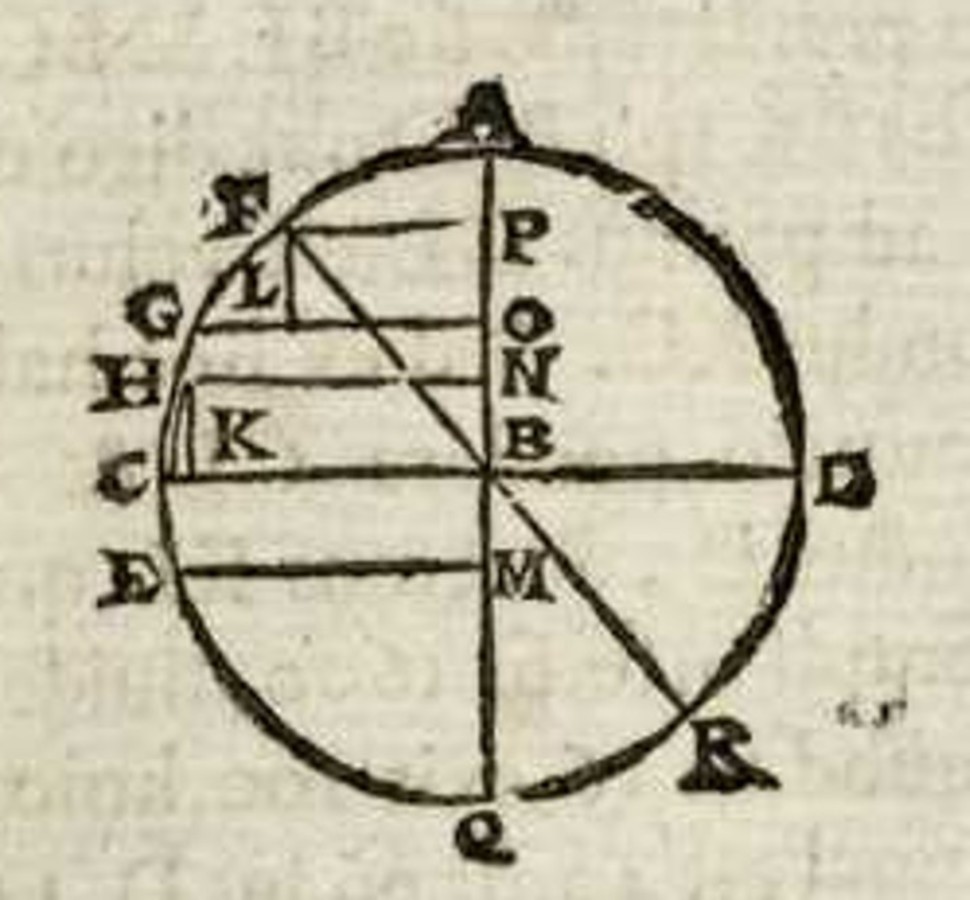
Fig. 3.9: According to Cardano, there are three ways to determine positional heaviness. The positional heaviness at point F, for instance, may be determined by the horizontal FP, by the vertical FL, or by the angle QBF.
3.6.2 Del Monte’s Critical Remarks on Positional Heaviness
Del Monte’s criticism of Benedetti, in the Meditatiunculae as well as in the margin- al remarks of his Diversae speculationes, are closely related to his criticism of Nemorarius
The center of gravity is a certain point within it, from which, if it is imagined to be suspended and carried, it remains stable and maintains the position which it had at the beginning, and is not set to rotation by that motion.11
Apart from the conceptual irreconcilability between his own approach and that of the Nemorarius
Contrary to the assumptions of Nemorarius
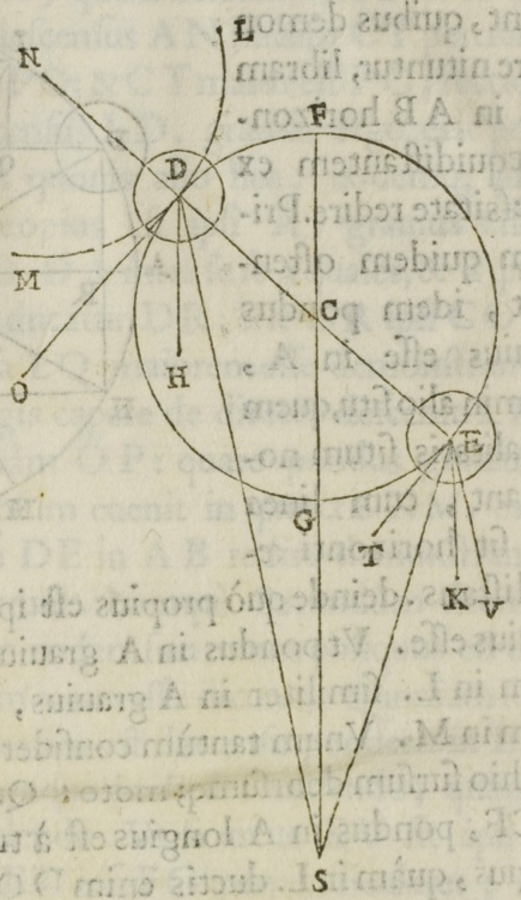
Fig. 3.10: According to del Monte, if S represents the center of the world, then the mixed angle SEG between the circular path of the weight at E and the direction to the center of the world is less than the mixed angle SDG. Thus, contrary to what his adversaries claim, by their own suppositions the weight placed at E must be heavier than that placed at D.
Del Monte objected that, from the point of view of positional heaviness, it is not in the horizontal position that a body weighs the most but at that point where a straight line drawn from the center of the world touches at a tangent the circle described by the balance arm. Certainly, if the center of the world were infinitely distant and all lines of direction converging at it were perpendicular and parallel to each other, then the extreme point would mark the horizontal position of the balance arm, also at the fulcrum. Still, for a finite distance from the center of the world, the point where the weight is heaviest lies instead slightly below the horizontal through the fulcrum. Del Monte even demonstrated that the closer the balance is to the center of the world, the further this “extreme point” (where the weight is heaviest) will lie from the horizontal position of the balance arm (as seen from the fulcrum).
Del Monte’s crucial objection to the Nemorarius
3.6.3 Benedetti on Tartaglia’s and Nemorarius’s
Benedetti confronted the ideas of Tartaglia and Nemorarius
More specifically, Benedetti refuted several of Tartaglia’s claims. In particular, he disputed the central thesis that when a balance is moved from its horizontal position, it will return to this position because the body that has moved upward will attain greater positional heaviness than the body which has moved downward. As we have seen above, Jordanus’s
Nevertheless, Benedetti did not believe in an indifferent equilibrium of such a balance when considered in a cosmological context. In the continuation of his argument, he came to the conclusion (correct from a modern viewpoint) that when such a balance in equilibrium is displaced from its original horizontal position, the weight that has been lowered will actually assume a greater positional heaviness than the one that has been lifted up:
Therefore the weight of A in this [lower] position will be heavier than the weight of B.12
He reached this conclusion by taking into account that the lines of inclination of the two weights are not parallel to each other but must converge at the center of the elements. The effective lever arms of the two weights must hence be determined by perpendicular lines drawn from the center of the balance to these lines of inclination. It now turned out that the perpendicular line, corresponding to the weight that had been lowered, is longer than the line corresponding to the weight that had been lifted. Consequently, the lower weight had become heavier positionally so that one would expect the balance to tilt into a vertical position.
Benedetti added some more critical remarks on Tartaglia’s consideration of positional heaviness. As we have seen, Tartaglia
Now the whole error into which Tartagliaand Jordanus fell arose from the fact that they took the lines of inclination as being parallel to each other.13
In summary, Benedetti introduced a way of determining the positional effect of a weight or a force that, in the cases he considered, essentially produces the same results as the application of the modern concept of torque. In particular, Benedetti had managed to go beyond the consideration of weights tending downward to include forces acting in an arbitrary direction. In this way, he was also able to take into account the fact that, on a spherical Earth, the lines of inclination of weights on a balance are not parallel. He did not manage, however, to successfully apply his measure of positional heaviness to challenging objects such as the inclined plane.
3.7 Conclusions: The Triangulation Benedetti-del Monte-Galileo
In this chapter, we have dealt with del Monte’s and Benedetti’s different approaches to mechanics emerging from their reflection on the balance and their treatment of earlier authors. Relative to the issue of positional heaviness, del Monte’s self-positioning is essentially external whereas Benedetti positioned himself within the tradition of the Nemorarius
In conclusion, it may be useful to recall the problems linked to the triangulation Benedetti-del Monte-Galileo
There are a number of possible connections between Benedetti and Galileo
Another potential intermediary was Galileo’s
An important clue is page 145bis of the Meditatiunculae (Figure 3.11), which is the page opposite the one containing the detailed criticism of Benedetti dealt with in this chapter. This page shows Galileo’s
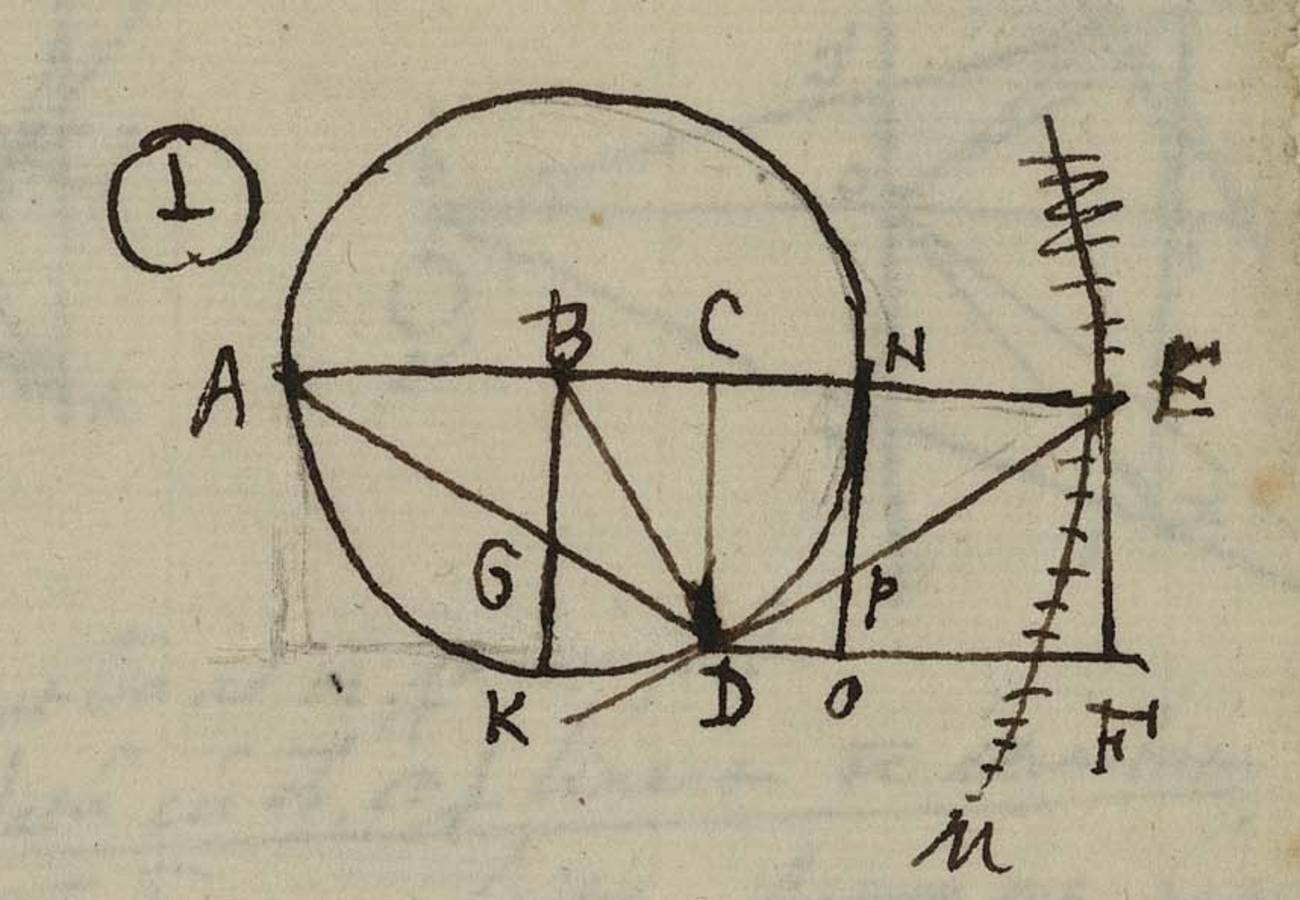
Fig. 3.11: Del Monte, Meditatiunculae, p. 145bis showing Galileo’s
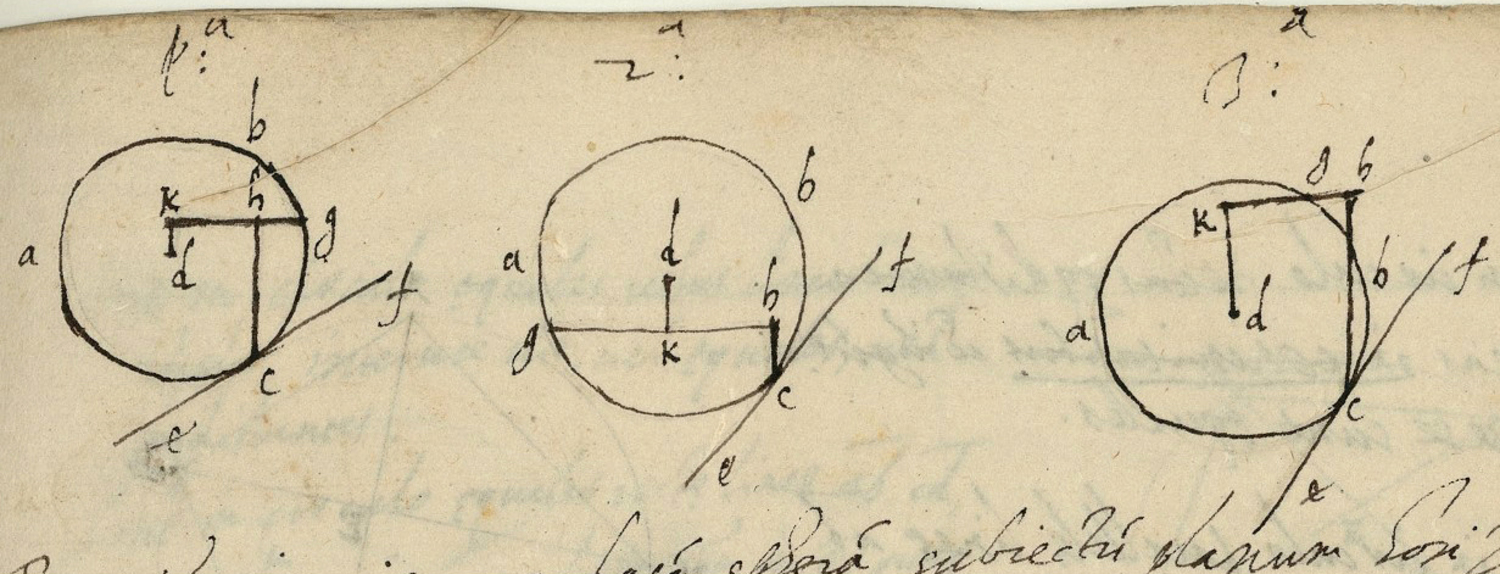
Fig. 3.12: Del Monte’s construction related to the inclined plane on p. 64 of his notebook. The construction was adapted from Pappus’s
This fact is all the more noteworthy since del Monte’s notebook, on an earlier page, also contains his own problematic adoption of Pappus’s
Recent research into del Monte’s biography has shown that del Monte and Galileo
In particular, Galileo’s
Center of gravity is defined to be that point in every heavy body around which parts of equal moments are arranged.22
The evidence for this claim concerning Benedetti’s legacy in Galileo’s
According to Benedetti and Galileo
There is one thing that must be considered before proceeding further, and this concerns the distances at which heavy bodies come to be weighed; for it is very important to know the sense in which equal and unequal distances are to be understood, and in what manner they must be measured.23
In his analysis of the inclined plane using the bent lever, Galileo
In conclusion, the very existence of del Monte’s annotations on his copy of Benedetti’s Diversarum speculationum […] liber provides a definitive answer to the question of who actually read this book.24
3.8 Appendix 1: Benedetti’s De Mechanicis, Chapters I–III
DE MECHANICIS
Scripserunt multi multa, et quidem scitissime, de mechanicis, at cum natura ususque aliquid semper vel novum, vel latens in apertum emittere soleant, nec ingenui aut grati sit animi, posteris inuidere, si quid ei contigerit comperuisse prius tenebris involutum: cum tam multa ipse ex aliorum diligentia sit consequutus. Paucula quaedam futura, ut reor, non ingrata his qui in hisce mechanicis versantur, nusquam ante hac tentata, aut satis exacte explicata in medium proferre volui: quo vel iuvandi desiderium, vel saltem non ociosi ingenioli argumentum aliquod exhiberem: atque vel hoc uno modo me inter humanos vixisse testatum relinquerem.
3.8.1 De differentia situs brachiorum librae. CAP. I.
Omne pondus positum in extremitate alicuius brachii librae maiorem, aut minorem gravitatem habet, pro diversa ratione situs ipsius brachii. Sit exempli gratia B centrum, aut, quod dividit brachia alicuius librae, et ABQ verticalis linea, aut, ut rectius dicam, axis orizontis, et BC unum brachium dictae librae, et in C sit pondus, et CO linea inclinationis, seu itineris C versus centrum mundi, cum qua BC angulum rectum constituat in puncto C. Existente igitur in huiusmodi situ brachio BC dico pondus C gravius futurum, quam in alio quolibet situ quia supra centrum B omnino non quiescet, quemadmodum in quovis alio situ faceret. Ad quod intelligendum, sit dictum brachium, in situ BF cum eodem pondere in puncto F et linea itineris seu inclinationis dicti ponderis sit FUM per quam lineam dictum pondus progredi non potest, nisi brachium BF breuius redderetur. Unde clarum erit quod pondus F aliquantulum supra centrum B mediante brachio BF nititur. Est quidem verum, quod pondus C nec ipsum etiam per lineam CO proficiscetur, quia iter extremitatis brachii est circularis, et CO in uno quodam puncto est contingens. Sit hoc iter ACQ oportet nunc praesupponere pondus extremitatis brachii debere tanto magis centro B inniti, quanto magis linea suae inclinationis (ponamus FUM) propinqua erit dicto centro B quod sequenti cap. probabo, ut exempli gratia, sit F super U punctum medii ex aequo inter C et B quapropter UB aequalis erit UC unde sequetur dictum pondus gravius futurum pro parte FC quam pro ea, quae est AF et minus supra centrum B pro dicta parte FC quam pro parte AF quieturum; et dictum brachium quanto magis orizontale erit a situ BF tanto minus supra dictum centrum B quiescet, et hac ratione gravius quoque erit, et quanto magis vicinum erit ipsi A a dicto F tanto magis super centrum B quoque quiescet, unde tanto quoque levius existet. Idem dico de omni situ brachii per girum inferiorem CQ ubi pondus pendebit a centro B dictum centrum attrahendo, quemadmodum superius illud impellebat. Haec vero omnia cap. sequenti melius percipientur.
3.8.2 De proportione ponderis extremitatis brachii librae in diverso situ ab orizontali. CAP. II.
Proportio ponderis in C ad idem pondus in F erit quemadmodum totius brachii BC ad partem BU positam inter centrum et lineam FUM inclinationis, quam pondus ab extremitate F liberum versus mundi centrum conficeret. Quod ut facilius intelligamus imaginemur alterum brachium librae BD et in extremo D locatum aliquod pondus minus pondere C ut BU pars BC minor est BD. Clare cognoscetur ex 6 lib. primi de ponderibus Archimedis, quod si in puncto U collocatum erit pondus ipsius C libra nihil penitus a situ orizontali dimovebitur. Sed perinde est quod pondus F aequale C sit in extremo F in situ brachii BF quam ut sit in puncto U in situ ipsius BU orizontali. Ad cuius rei evidentiam imaginemur filum, FU perpendiculare, et in cuius extremo U pendere pondus, quod erat in F unde clarum erit quod eundem effectum gignet, ac si fuisset in F quod, ut iam diximus remanens affixum puncto U brachii BU tanto minus grave est situ ipsius C quanto UB minus est ipso BC. Idem assero si brachium esset in situ EB quod facile cognoscere poterimus, si imaginemur filum appensum ipsi U brachii BC et usque ad E perpendicularem, in quo extremo appensum esset pondus aequale ponderi C et liberum ab E brachii BE unde libra orizontalis manebit. Sed si brachium BE consolidatum fuisset in tali situ cum orizontali BD et appenso pondere C in E libero a filo, nec ascenderet, neque descenderet, quia tantum est quod ipsum sit appensum filo, quod pendet ab U quantum quod ab ipso liberum appensum fuisset E brachii BE et hoc procederet ab eo quod partim penderet a centro B et si brachium esset in situ BQ totum pondus centro B remaneret appensum, quemadmodum in situ BA totum dicto centro anniteretur. Unde fit ut hoc modo pondus magis aut minus sit grave, quo magis aut minus a centro pendet, aut eidem nititur: atque haec est causa proxima, et per se, qua fit ut unum idemque pondus in uno eodemque medio magis aut minus grave existat. Et quamvis appellem latus BC orizontale, supponens illud angulum rectum cum CO facere, unde angulus CBQ fit ut minor sit recto, ob quantitatem unius anguli aequalis ei, quem duae CO et BQ in centro regionis elementaris constituunt, hoc tamen nihil refert, cum dictus angulus insensibilis sit magnitudinis. Ab istis autem rationibus elicere possumus, quod si punctus U erit ex aequo medius inter centrum B et extremum C pondus F aut M pendebit, aut nitetur pro medietate dicto centro B et si dictum U erit propius B quam puncto C pendebit ab ipso, aut nitetur ipsi amplius quam ex medietate, et si magis versus C minus quam ex medietate nitetur.
3.8.3 Quod quantitas cuiuslibet ponderis, aut virtus movens respectu alterius quantitatis cognoscatur beneficio perpendicularium ductarum a centro librae ad lineam inclinationis. CAP. III.
Ex iis, quae a nobis hucusque sunt dicta, facile intelligi potest, quod quantitas BU quae fere perpendicularis est a centro B ad lineam FU inclinationis, ea est, quae nos ducit in cognitionem quantitatis virtutis ipsius F in huiusmodi situ, constituens videlicet linea FU cum brachio FB angulum acutum BFU. Ut hoc tamen melius intelligamus, imaginemur libram BOA fixam in centro O ad cuius etrema sint appensa duo pondera, aut duae virtutes moventes E et C ita tamen quod linea inclinationis E id est BE faciat angulum rectum cum OB in puncto B. Linea vero inclinationis C id est AC faciat angulum acutum, aut obtusum cum OA in puncto A. Imaginemur ergo lineam OT perpendicularem lineae CA inclinationis, unde OT minor erit OA ex 18 primi Euclidis.
3.9 Appendix 2: Del Monte’s Meditatiunculae, ff. 145 and 146
Tassora’s
3.9.1 Contra Cap. 2 Jo. de Benedicti de Mechanicis
Inquit auctor in demonstratione idem pondus in F, aeque grave esse ut in U et in E. Quod est tamen falsum.
Nam lineae FM AQ non sunt aequidistantes, cum in centrum mundi conveniant.
Ac propterea ducta per U linea LUS ipsi AQ aequidistante; erit UL inter FU AB; UE vero inter US et BQ.
Quare ducta SRD, erit BD ad BU, ut DR ad RS. Ac propterea si BU dimidia est ipsius BD, et SR erit dimidia ipsius RD.
Si igitur ducatur BS, quae intelligatur consolidata cum BD ponaturque pondus in S duplum ponderis D, aequeponderabunt pondera SD ex distantiis BD RS ita constitutis, cum sit R ipsorum centrum gravitatis in linea BQ. Hoc est in infimo loco. Ut ex nostris mechanicis patet.
Pondus igitur in S aequegrave erit, atque U non autem pondus in E, ut ipse existimat. Idem enim pondus gravius est in S quam in E.
Ut ipse fatetur quod probabitur quoque hoc modo. Nam productis LS DE in X est quidem DZ ad ZX, ut DR ad RS. Atque maiorem habet proportionem DZ ad ZE, quam ad ZX; duplum igitur ponderis D in X ipsi D aequeponderabit. Positum ergo in E ipsi D non aequeponderabit. Et ut aequeponderet, maius erit quam duplum.
Similiter ad partem F ducta LGB quoniam LU est GB aequidistans; erit DG ad GL, ut DB ad BU. Si igitur intelligatur BL consolidata cum BD, idem pondus, tam in L, quam in U eidem ponderi in D aequeponderabit, cum G sit centrum gravitatis ponderum in L D existentium. Non igitur pondus in F aequegrave est, ut idem pondus in U.
Praeterea secet FD ipsam LU in H. Patet idem pondus in U et in H ipsi ponderi in D aequeponderare. Cum sit DK ad KH, ut DB ad BU, et DG ad GL. Minorem autem proportionem habet DK ad KF, quam ad KH. Minus igitur pondus in F quam duplum ipsius D, ipsi D aequeponderabit.
Et quibus etiam constat idem pondus in F, et in U, et in E, diversi modo gravitare. Gravius est enim in situ E quam in U et in F. In U vero gravius, quam in F.
Fallacia vero argumenti est cum inquit, existente filo FUE perpendiculari, idem pondus in F et in U eodem modo gravitabit. Quod est quidem verum, si intelligatur quod eodem modo gravitet in F a quo libere pendet.
Cum vero inquit, quoniam punctum fili U secet BC in U, ergo pondus in puncto U librae DBU, ac propterea in U brachii BU eandem habebit gravitatem ut in F; est falsum. <Nunc> enim valet consequentia pondus in filo in U eandem habet gravitatem ut in F. Ergo pondus in U brachii BU eandem habet gravitatem ut in F. Veluti quoque falsum est propter filum pondus in E est aequegrave, ut pondus in U brachii BU. Non est igitur haec vera et proxima causa, et per se harum gravitatum. Ut ipse profitetur.
3.9.2 Against Chapter 2 of Giovanni Benedetti’s [treatise] on Mechanics
The author claims in his proof that the same weight in F is equally heavy as in U and in E, but this is false.
The lines FM AQ are namely not equally distant, because they converge in the center of the world.
And therefore if the line LUS is drawn through U equidistant to AQ, UL will be between FU AB, but UE between US and BQ.
For if one draws SRD, BD will be to BU, as DR to RS. And hence if BU is half of the same BD, also SR will be the half of the same RD.
If therefore BS is drawn, which shall be understood as being rigidly connected with BD, and if a weight is placed in S which is double the weight [in] D, the weights SD will be in equilibrium from the distances BD RS thus constituted, because their center of gravity R is in the line BQ; that is in the lowest place; as is evident from our [book on] mechanics.
The weight in S will therefore be equally heavy as [the weight in] U but not as the weight in E as he believes. The same weight is namely more heavy in S than in E.
As he himself admits this can also be proven in the following way. Because when LS DE are prolongued [to meet ] in X, then evidently DZ is to ZX as is DR to RS. But DZ has a larger proportion to ZE than to ZX; the double of the weight D in X will therefore be equally heavy as the same D. Hence placed in E it will not be equally heavy as D. And if it were in equilibrium, it would be more than double.
Similarly let LGB be drawn to F being LU equidistant to GB; DG will be to GL as DB to BU. If now BL is understood as being connected with BD, the same weight, in L as in U will be in equilibrium with the same weight in D, because G is the center of gravity of the weights existing in L and D. Therefore the weight in F is not equally heavy as the same weight in U.
Let furthermore FD cut the same LU in H. It is clear that the same weight in U and in H will be equally heavy with regard to the same weight in D. Because DK is to KB as is DB to BN and as DG to GL. But DK has a smaller proportion to KF as to KH. Therefore in F a weight smaller than double [the weight in] D will be in equilibrium with the same weight D.
From this it is also clear that the weight in F, in U, and in E gravitates in a different ways. It is namely heavier in the position E than it is in U and in F. But in U it is heavier than in F.
But the fallacy of the argument emerges when he says that, being the thread FUE perpendicular, the weight in F has the same heaviness as in U. What is indeed true if it is understood that it gravitates in the same way in F from which it freely hangs.
But if he says, because the point of the thread U cuts BC in U, therefore the weight in the point U of the balance DBU will hence have the same heaviness in U of the lever arm BU as in F, then this is false. Now the consequence holds that the weight on the thread in U has the same heaviness as in F. Thus, the weight in U of the beam BU has the same heaviness as in F. In the same way it is also false that because of the thread the weight in E is equally heavy as the weight in U of the arm BU. This is therefore not the true and next cause, and [the cause] itself [per se] for them of these heaviness [proportions], contrary to that which he contends.
3.9.3 Contra <capitulum> 3 eiusdem
Falsum est igitur ex dictis, quod in principio tertii <capitoli> inquit. Praeterea demonstratio falsa quoque videtur.
Inquit enim sint E C duo pondera, aut duae virtutes, ita ut intelligat, et supponat virtutes ponderum officio fungi. Intelligantur itaque ad maiorem evidentia duo pondera E C. Sitque BAC angulus primum acutus.
Et quoniam pondus (inquit) in I aequale C ipsi <E> aequeponderat, cum sit pondus C ad pondus E, ut BO ad OI. Quia vero facta est OI aequalis OT inquit.
Si loco OI imaginabimur OT consolidata cum OB, et per lineam TC attractam virtute C, similiter quoque continget, ut BOT, communi quadam scientia, non moveatur situ.
Fateor me hanc quamdam communem scientiam non intelligere.
At perpendamus sensum quod nil aliud significat, nisi quod idem pondus ipsi C aequale, in I, rectam libram BOI, idemque pondus C consolidatam libram BOTC, ponderi E aequeponderat. Quod esse non potest.
Nam si intelligatur linea BA horizonti aequidistans. Centroque O circulus describatur IT, idem pondus gravius erit in I, quam in T.
Quare pondus in T ipsi C aequale non aequeponderabit libram TOB.
Quod patet etiam ducta primum OQ linea perpendiculari, quam ipse lineam verticalem, et axem horizontis nuncupat. Deinde ducatur ID ipsi OQ aequidistans, ducaturque BFTD: erit BF ad FD, ut BO ad OI. Si igitur intelligatur OD consolidata cum OB, idem pondus in D ipsi E aequeponderabit, cum punctum F ponderum in BD centrum gravitatis <existens> sit in linea OFQ. Pondus ergo in T ipsi E non aequeponderabit. Multoque minus pondus C ipsi E aequeponderare potest.
Nam si iungatur BC, fiatque ut C ad E, ita BS ad SC; erit S ponderum centrum gravitatis. Quod quidem in linea OQ existere non potest.
Productis enim ID BC in X; erit BO ad OI, ut BU ad UX. Quare ducta OX, quae intelligatur consolidata cum BO, pondus in X aequale ipsi C ponderi E aequeponderabit. Itaque existente pondere C in recta linea BCX, intelligaturque ducta CO consolidata cum OB; pondus C non aequeponderabit E.
Idem enim sequitur sive intelliganturque CO OB consolidatae, sive CT TO OB consolidatae. Non enim punctum U esse potest centrum gravitatis ponderum in B C existentium. Cum maiorem habeat proportionem BU ad UC quam ad UX, ac propterea maiorem quam pondus C ad E. Quare centrum gravitatis S ponderum in CB est inter UB. Numquam autem manebit libra COTB, donec punctum S sit in linea OQ. Ergo non aequeponderabunt.
Similiter existente BAC angulo obtuso, ostendetur pondus in T minorem habere gravitatem, quam in I.
Deinde pondus in X aequale ipsi C aequeponderare ipsi E; cum sit BU ad UX, ut BO ad OI.
Si itaque sit S centrum gravitatis ponderum in B C; erit S inter UC. Quare cum non sit S in linea OQ. Pondera C e consolidatam libram CTOB non aequepoberabunt.
Falsa igitur est demonstratio. Fallacia vero est, cum inquit, continget, ut BOT communi quadam scientia, non <moveatur> situ.
Et est omnino falsum si intelligatur C esse pondus, quod in centrum mundi sempre tendit. Ut ipse supponere videtur. Et ut ipse in seguentibus <capitolis> accipit hoc tamquam de ponderibus demonstratum.
At vero si intelligatur I potentia movens, ut hominis, qui potest trahere T per rectam lineam TC, tunc vera esse potest demonstratio. Ut patet ex tractatum de axe in peritrochio nostrorum Mechanicorum.
Notandum tamen, quod conclusiones per communem quandam scientiam deductae, non sunt periti mathematici cum propriis uti oporteat.
Ex hac etiam figura magis patet absurdum, hoc est pondera E C aequeponderare non posse.
3.9.4 In Opposition to Chapter 3
It is therefore false, from what has been said, what he says in the beginning of the third chapter. Moreover also the demonstration seems to be wrong.
He says namely that E and C are two weights, or two forces, so that he understands and assumes that the forces take over the role of the weights. Let therefore, for major clarity, E and C be understood to be two weights. And let BAC first be an acute angle.
And since (he says) the weight in I equal to C will be equally heavy to that in <E>, because the weight C is to the weight E as is BO to OI. Because OI is made equal to OT he says.
If we shall imagine instead of OI OT to be rigidly connected with OB, and along the line TC attracted by the force C, it is also similarly the case that BOT, by a certain common science, will not change place.
I admit that I do not understand this certain common science.
We guess that this means nothing else but that the same weight, equal to C, in I, by the straight balance BOI, and the same weight C, if the balance BOTC is [conceived to be] solid, will be equally heavy to the weight E. Which cannot be.
For if it is understood that the line BA is equidistant from the horizon, and a circle IT is described with center O, the same weight will be heavier in I than in T.
Because the weight in T, equal to that [in] C, will not be in equilibrium with the balance TOB.
This is also evident when one first draws the line OQ perpendicularly, which he calls vertical line and axis of the horizon. Then let ID be drawn equidistant to OQ, and let BFTD be drawn: then BF will be to FD, as BO to OI. If therefore OD is understood as being rigidly connected with OB, the same weight in D will be in equilibrium with the same E, because the point F, the center of gravity of the weights in BD, is in the line OFQ; hence the weight in T is not in equilibrium with the weight E. And a much less smaller weight C can be in equilibrium with the same E.
For if BC is connected, and if we let as C to E, be BS ad SC, then S will be the center of gravity of the weights. This [center], however, cannot exist in the line OQ.
If namely ID BC are prolongued [to meet] in X; then BO will be to OI as BU to UX. For which reason if OX is drawn, which is understood as being rigidly connected with BO, the weight in X, equal to the same C will be in equilibrium with the weight E. Therefore, if the weight C exists in the straight line BCX, and if it is understood that CO is drawn [and] rigidly connected with OB, the weight C will not be in equilibrium with E.
The same follows namely when alternatively CO and OB are understood to be rigidly connected, or when CT, TO, and OB are connected. For the point U cannot be the center of gravity of the weights existing in B C. Because BU has to UC a larger proportion than to UX, and hence a major [proportion] than the weight C to E. Because the center of gravity S of the weights in CB is between UB. But the balance COTB will never remain, as long as the point S is in the line OQ. Therefore they will not be in equilibrium.
Similarly, if there is an obtuse angle BAC, it is shown that the weight in T has a smaller heaviness than in I.
Then the weight in X equal to the same C [is claimed] to be in equilibrium to the same E; because BU is to UX, as is BO to OI.
If therefore S is the center of gravity of the weights in B C, S will be between UC. For which reason because S is not in the line OQ, the weights C and the rigidly connected balance CTOB will not be in equilibrium.
The demonstration is therefore false. Actually, the fallacy is [to say] that BOT, according to some common science, does not <change> its place.
And it is totally false if C is understood to be a weight which always tends to the center of the world as he seems to assume and as he in the following <chapters> assumes it to be demonstrated as if it holds for weights.
To speak the truth, if I is understood to be a moving power, like that of a man who can draw T along the straight line TC, then the demonstration can be true. In fact, it is clear from our treatise on the axis on the wheel [de axe in peritrochio] of our Mechanics.
It nevertheless has to be noted that the conclusions which are inferred by a certain common science should not be used by an experienced mathematician because he should use his own.
From this figure descends an even greater absurdity, namely that the weights E C cannot be in equilibrium.
References
Benedetti, G. B. (1585). Diversarum speculationum mathematicarum, et physicarum liber: quarum seriem sequens pagina indicabit. Torino: Bevilaqua.
Bertoloni Meli, D. (2006). Thinking with Objects: The Transformation of Mechanics in the Seventeenth Century. Baltimore: Johns Hopkins University Press.
Bordiga, G. (1985). Giovanni Battista Benedetti: filosofo e matematico veneziano del secolo XVI. Con un aggiornamento bibliografico ragionato di Pasquale Ventrice. Venezia: Istituto Veneto di Scienze, Lettere ed Arti.
Cardano, G. (1550). Hieronymi Cardani Medici Mediolanensis de subtilitate libri XXI. Nürnberg: Petreius.
Carugo, A., L. Geymonat (1958). Galieo Galilei: Discorsi e dimostrazioni matematiche intorno a due nuove scienze. Torino: Boringhieri.
Di Bono, M. (1987). L'astronomia copernicana nell'opera di Giovan Battista Benedetti. In: Cultura, scienze e tecniche nella Venezia del Cinquecento Venezia: Istituto Veneto di Scienze, Lettere ed Arti 283-300
Drake, S., I. E. Drabkin (1969). Mechanics in Sixteenth-Century Italy. Madison: University of Wisconsin Press.
Freudenthal, G. (2005). The Hessen-Grossman Thesis: An Attempt at Rehabilitation. Perspectives on Science 13(2): 166-193
Galilei, G. (1960a). On Mechanics. Translated with Introduction and Notes by Stillman Drake. In: On Motion and on Mechanics Ed. by I. E. Drabkin, S. Drake. Madison: The University of Wisconsin Press 133-186
- (1960b). On Motion. Translated with an Introduction and Notes by I. E. Drabkin. In: On Motion and on Mechanics Ed. by I. E. Drabkin, S. Drake. Madison: The University of Wisconsin Press 1-131
- (1968). G. Galilei, Le opere. Florence: Barbera.
- (2002). Le mecaniche. Firenze: Olschki.
Galluzzi, P. (1979). Momento. Studi galileiani. Roma: Ed. dell'Ateneo & Bizzari.
Giusti, E. (1998). Elements for the Relative Chronology of Galilei's “De motu antiquiora”. Nuncius XIII: 427-460
Hispanus, P. (1972). Tractatus sive summule logicales..
Mazzoni, J. (1597). In universam Platonis et Aristotelis philosophiam praeludia. Venezia: Guerilius.
Monte, Guidobaldo del (1577). Mechanicorum liber. Pesaro: Hieronymum Concordiam.
- (1587). Meditantiunculae Guidi Ubaldi ex marchionibus montis Santae Mariae de rebus mathematicis (ca. 1587-1592)..
Nemorarius, J. (1533). Liber Jordani Nemorarii viri clarissimi de ponderibus proportiones XIII et earundem demonstrationes, multarumque rerum rationes sane pulcherrimas complectens, nunc in lucem editus cum gratia et privilegio imperiali, Petro Apiano mathematico ingolstadiano ad xxx. annos concesso. Nürnberg: Petreius.
- (1565). Jordani opusculum de ponderositate Nicolai Tartaleae studio correctum, novisque figuris auctum. Venezia: Curzio Troiano Navo.
Omodeo, P. D. (2009). La cosmologia infinitistica di Giovanni Battista Benedetti. Bruniana & Campanelliana 15(1): 181-190
Renn, J., P. Damerow (2010). Guidobaldo del Monte's Mechanicorum liber. Berlin: Edition Open Access.
- (2012). The Equilibrium Controversy: Guidobaldo del Monte's Critical Notes on the Mechanics of Jordanus and Benedetti and their Historical and Conceptual Background. Berlin: Edition Open Access.
Renn, J., P. Damerow, P. D. (2001). Hunting the White Elephant. When and How Did Galileo Discover the Law of Fall?. In: Galileo in Context Ed. by J. Renn. Cambridge: Cambridge University Press 29-149
Sarpi, P. (1996). Pensieri naturali, metafisici e matematici. Milano: Ricciardi.
Tassora, R. (2001) Le Meditatiunculae de Rebus Mathematicis di Guidobaldo del Monte. Ph. D. thesis. Università di Bari
Footnotes
This chapter draws on a talk delivered by Jürgen Renn and Peter Damerow entitled “Guidobaldo’s marginal notes on Benedetti’s Diversarum speculationum.” It presented for the first time del Monte’s marginal notes in his copy of Benedetti’s Diversae speculationes. These marginal notes have meanwhile been published with a commentary in the Edition Open Access series of the Max Planck Research Library for the History and Development of Knowledge under the title The Equilibrium Controversy. The loss of our dear colleague Peter Damerow has forced us to shift the focus of this contribution.
A first analysis and an overview of del Monte’s handwritten work has been carried out by Roberta Tassora in her Ph.D. dissertation (Tassora 2001). This is freely available from the ECHO website at http://echo.mpiwg-berlin.mpg.de/content/mpiwglib/pesaro/tassora.
The last treatise is dealt with in many letters.
We are grateful to Dominik Perler for a helpful discussion of this point, as well as for his suggestions of pertinent literature.
“Hoc primum caput to[tum] desumptum est a n[ostro] Mechanicorum libri tractatu de lib[ra].”
“[…] unde fit ut hoc modo pondus magis aut minus a centro pendet aut eidem nititur: atque haec est cause proxima, et per se [...].”
“non est neque proxima neque per se; nam [pond]us in F brachii [BF] non est equegrave ut pondus in U brachii BU; [nec] pondus in E brachii BE est equegrave ut pondus [in] U brachii BU. Unde tota haec demonstratio falsa est” (Renn and Damerow 2012, 207).
“si intelligamus p[ondus] in C, ut supponi p[otest] ex verbis ipsius, intelligendum est C[T] quoque consolidatam consolidatis TO […]. Unde si intelligamus C pondus et non movens, falsa est i[ta]que si intelligatur C movens ut homi[…] vera esse pote[st] quod [deleted: non] moveat non esse pondus s[i...] ipse [vero] in sequenti accipiat [hoc atque ponderi?] posse demonstratum quare nihil […] ut patet in 7 cap. In his duobus cap. fundantur omnes authoris demonstrationes ita ut sunt praecipua mechanicorum fundamenta quorum cognita falsitate omnia rem[oventur]” (Renn and Damerow 2012, 213).
We are grateful to Martin Frank who discovered these annotations and shared them with us.
“Aristoteles dicit hoc contingere, quum trutina est supra libram, quia angulus QBF metae, maior est angulo QBR. Et similiter quum trutina fuerit QB, erit meta AB, et tunc angulus RBA, maior erit angulo FBA, sed maior angulus reddit gravius pondus. […] Generalis igitur ratio haec sit: pondera quo plus distant a meta seu linea descensus per rectam aut obliquum, id est, per angulum, eo sunt graviora” (Cardano 1550, 17–18).
“Centrum gravitatis uniuscuiusque corporis est punctum quoddam intra positum, a quo si grave appensum mente concipiatur, dum fertur, quiescit; et servat eam, quam in principio habebat positionem: neque in ipsa latione circumvertitur” (Monte 1577, 1r). Translation in (Drake and Drabkin 1969, 259), revised in (Renn and Damerow 2010, 57).
“Pondus igitur ipsius A in huiusmodi situ, pondere ipsius B gravius erit” (Benedetti 1585, 148). Translation in (Drake and Drabkin 1969, 176).
“Omnis autem error in quem Tartalea, Iordanusque lapsi fuerunt ab eo, quod lineas inclinationum pro parallelis vicissim sumpserunt, emanuit” (Benedetti 1585, 150). Translation in (Drake and Drabkin 1969, 177).
See the discussion by Ventrice in (Bordiga 1985, 732–736) who mentions Drake, Drabkin, Fredette and Galluzzi among those who are skeptical about a concrete influence of Benedetti on Galileo. Notable exceptions are the commentaries by Carugo and Geymonat in their edition of Galileo’s Discorsi (Carugo and Geymonat 1958). Bertoloni Meli even considers the possibility of del Monte and Galileo discussing Benedetti, but nevertheless rejects any substantial influence by the latter on Galileo’s thinking because that influence supposedly would have arrived too late, see (Bertoloni Meli 2006, 61–65).
For an overview of such potential connections, see the discussion in (Bordiga 1985, 732–736) who also mentions Mersenne, Clavius and Cardinal Michelangelo Ricci as possible intermediaries.
For an overview, see (Bordiga 1985).
See, for instance, (Drake and Drabkin 1969, 36).
See (Benedetti 1585, 183–184). For a historical discussion of the context of this argument in contemporary technology, see (Freudenthal 2005).
For a thorough discussion of the chronology of these writings, see (Giusti 1998).
This scenario was developed in a joint discussion with Pier Daniele Napolitani. Concerning Benedetti’s adherence to the Copernican system, see (Di Bono 1987; Omodeo 2009).
See the extensive discussion in (Galluzzi 1979).
“Centro della gravità si diffinisce essere in ogni corpo grave quel punto, intorno al quale consistono parti di eguali momenti” (Galilei 1968, vol. 2, 159). Translation in (Galilei 1960a, 151). See also (Galilei 2002).
“Un’altra cosa, prima che più oltre si proceda, bisogna che sia considerata; e questa è intorno alle distanze, nelle quali i gravi vengono appesi: per ciò che molto importa il sapere come s’intendano distanze eguali e diseguali, ed in somma in qual maniera devono misurarsi” (Galilei 1968, vol. 2, 164). Translation in (Galilei 1960a, 156–157).
The knowledge that he had read it, however, is not entirely new. See (Renn et.al. 2001, 74).