Chapter structure
- 7.1 Introduction
- 7.2 Guidobaldo’s Possible Sources of Inspiration
- 7.3 Guidobaldo Changing the Foundation of Perspective
- 7.4 Guidobaldo’s Main theorem and Perspective Constructions
- 7.5 Guidobaldo’s Other Contributions to Perspective
- 7.6 Guidobaldo’s Influence on the Academic Approach
to Perspective - 7.7 Conclusion
- Acknowledgement
- References
- Footnotes
7.1 Introduction
When Guidobaldo Marchese del Monte is mentioned in the history of science it is most often for his contributions to mechanics. Thus, in the first edition of the Dictionary of Scientific Biography Paul Lawrence Rose
My plan is to show that Guidobaldo deserves the title of “The father of the mathematical theory of perspective,” as I have given him in this paper. I shall also make it clear that his insights did not come to him so easily and that he did not seem to have completely realized what a powerful instrument he had added to the toolbox for dealing with the theory of perspective.
7.2 Guidobaldo’s Possible Sources of Inspiration
In surveying the literature on perspective with a geometrical approach that appeared before Guidobaldo’s Perspectivae libri sex I only consider Italian works, because although authors North of the Alps published on perspective, none of them showed an interest in providing their readers with a mathematical understanding of the subject. The starting point is a work that does not have a particular mathematical approach, but is important because, directly or indirectly it is the source of inspiration for all other Italian literature on perspective. The work in question is Leon Battista Alberti’s
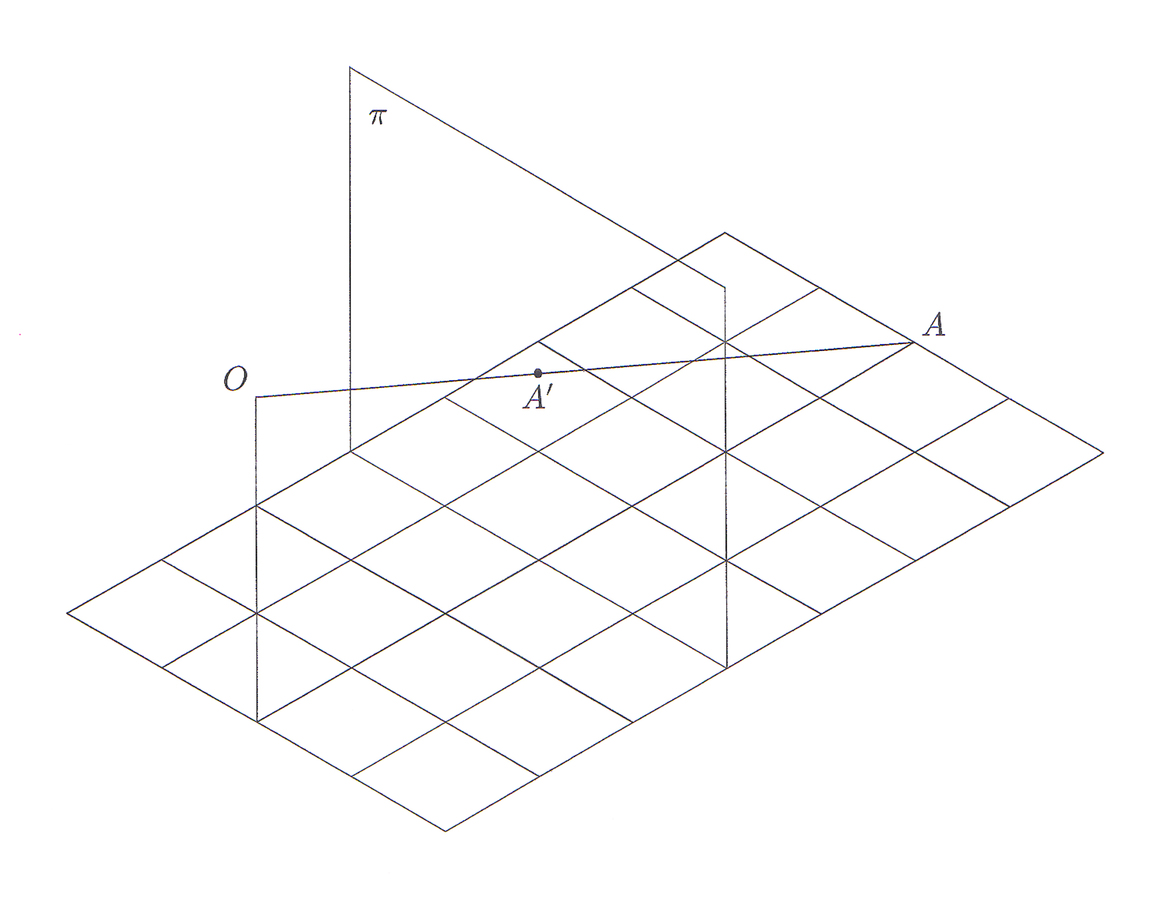
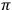 with respect to a given eye point
with respect to a given eye point Ois the point A’ where the line OA intersects
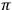 .
.Fig. 7.1: Alberti’s way of introducing what soon after him was called perspective involved the optical concept of a visual pyramid and the concept of a section in a visual pyramid. In a simplified version it corresponds to saying that for a given point A, its image in a given picture plane
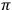 with respect to a given eye point
with respect to a given eye point O is the point A’ where the line OA intersects
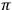 .
.
Alberti
Fig. 7.2: In De pictura Alberti describes how to make the perspective image of a grid of horizontal squares. This served as a kind of coordinate system that helped painters to decide where images of objects placed on a pavement with square tiles should be depicted in the picture plane.
In his book he did not explain the geometry that led him to his construction claiming that he wanted to outline “as a painter speaking to painters [...] the first rudiments of the art of painting.”1
There is no obvious way of reconstructing Alberti’s
Actually, Alberti
The assumption that the images of orthogonals meet, if extended, in one point, I hereafter called the convergence rule for orthogonals—and I use the expression that the orthogonals converge at the point of intersection. This rule was actually applied without question by most pre-seventeenth-century authors on perspective and was one of the foundations of the majority of the various methods used for constructing the image of a horizontal square suggested by these authors.2 Only the two Italian mathematicians, Federico Commandino
Most of Alberti’s
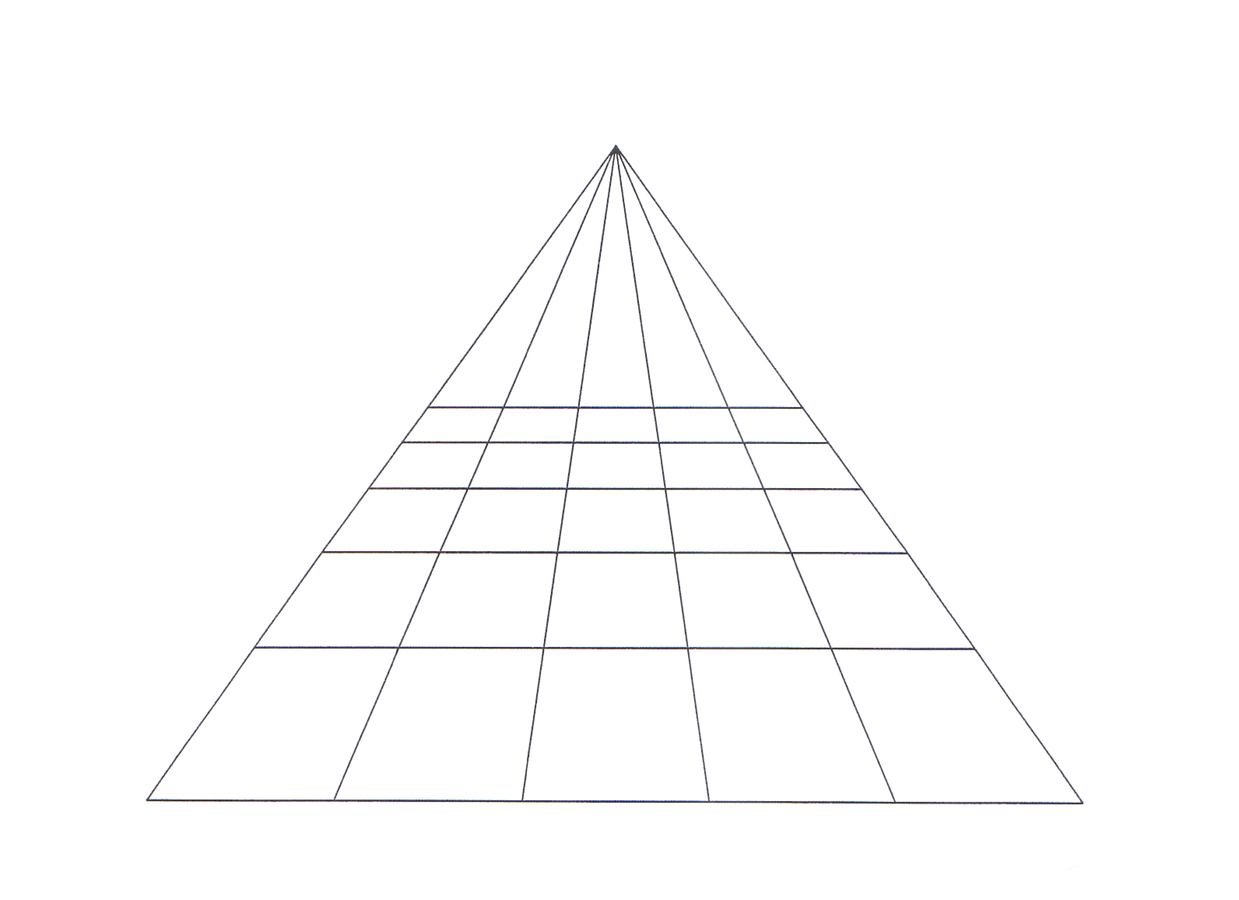
Fig. 7.3: Illustration of Alberti’s tacit rule: the images of orthogonals converge at one point in the picture plane.
Fig. 7.4: The orthogonal projection of the eye point O upon the picture plane, the point P, is Alberti’s
Besides taking the convergence rule for orthogonals for granted, Piero
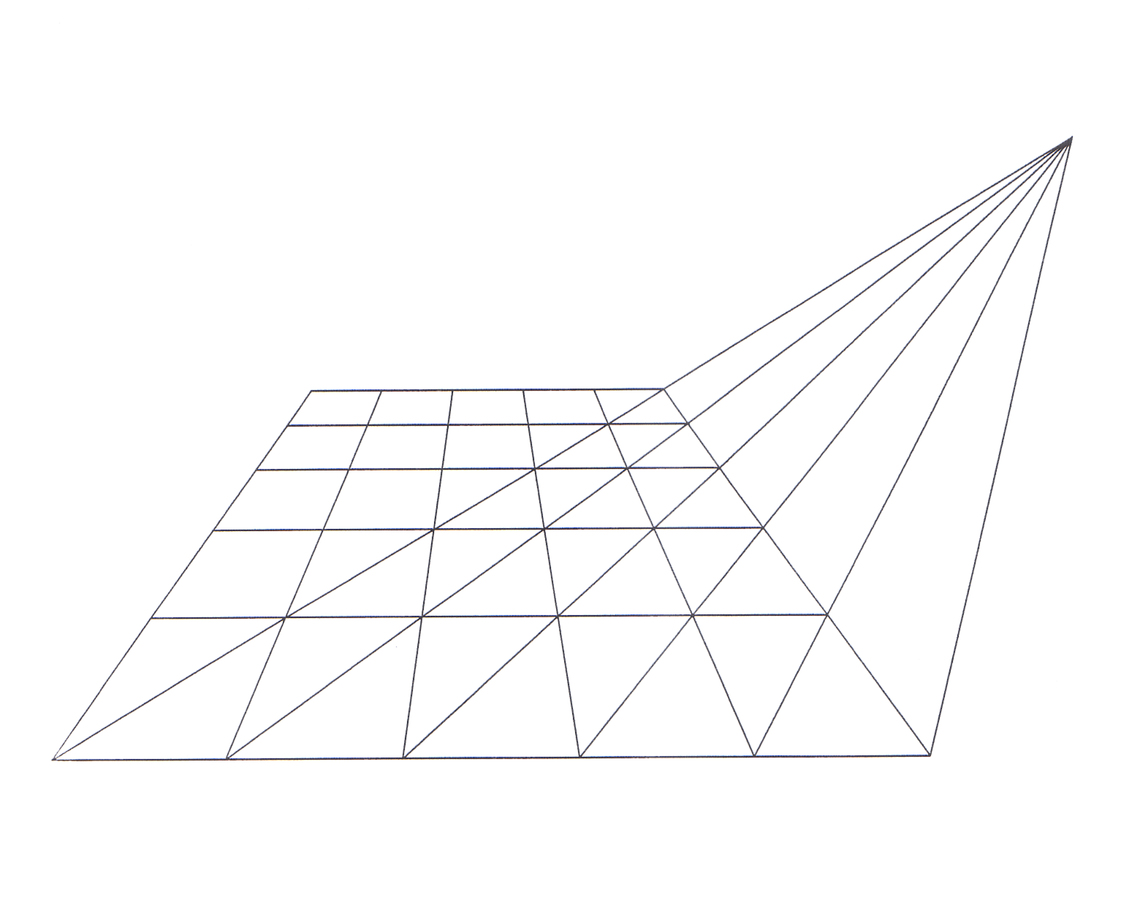
Fig. 7.5: Illustration of the rule applied by Piero della Francesca
He also described the position of this—to which I return in connection with Vignola
Piero’s
Commandino’s
Although Commandino’s
Danti’s
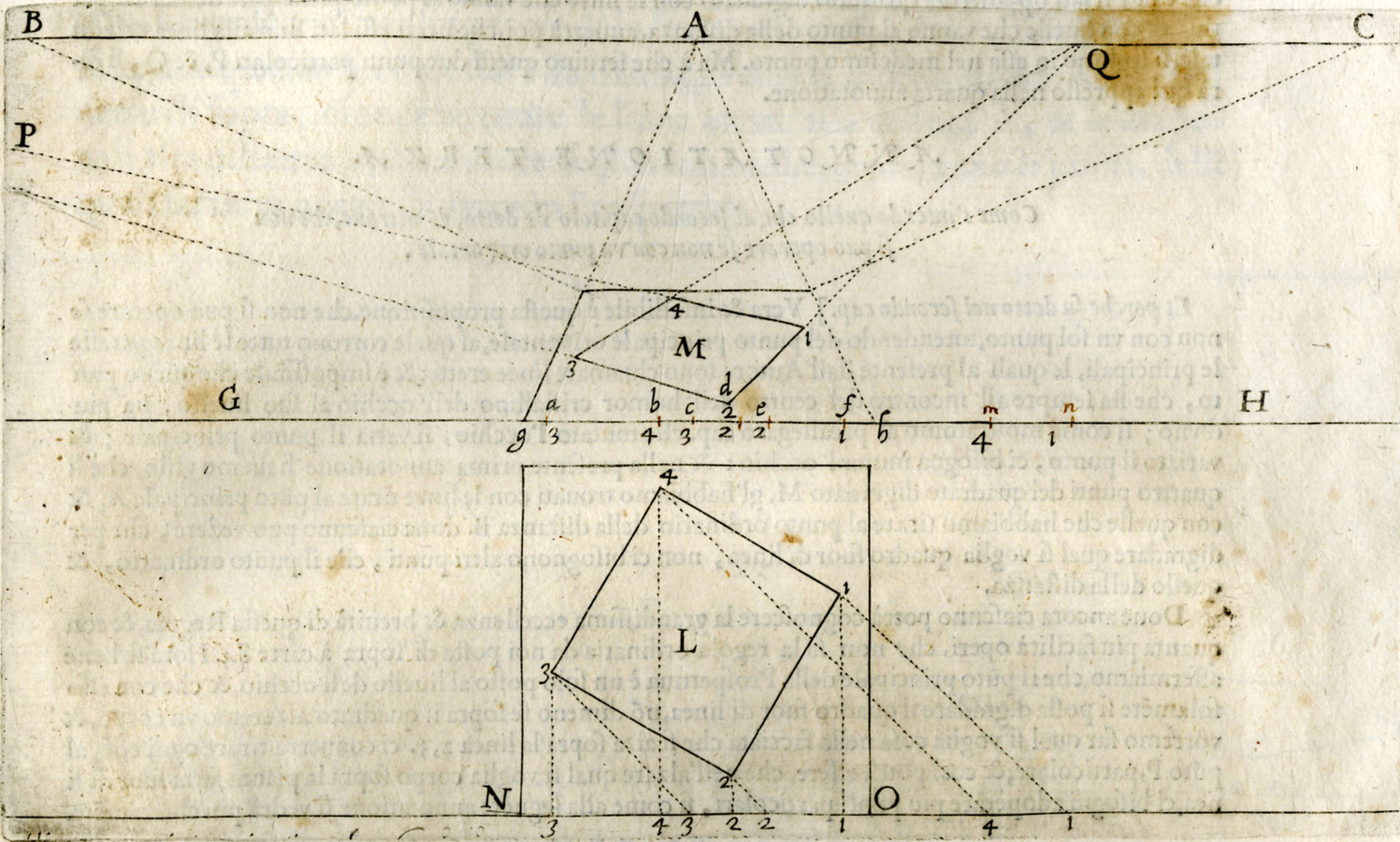
Fig. 7.6: Vignola illustrating that other lines than orthogonals and diagonals can have convergence points (Vignola 1583, 115; with kind permission of the Biblioteca Oliveriana, Pesaro).
Vignola’s
His commentator, the mathematician Danti
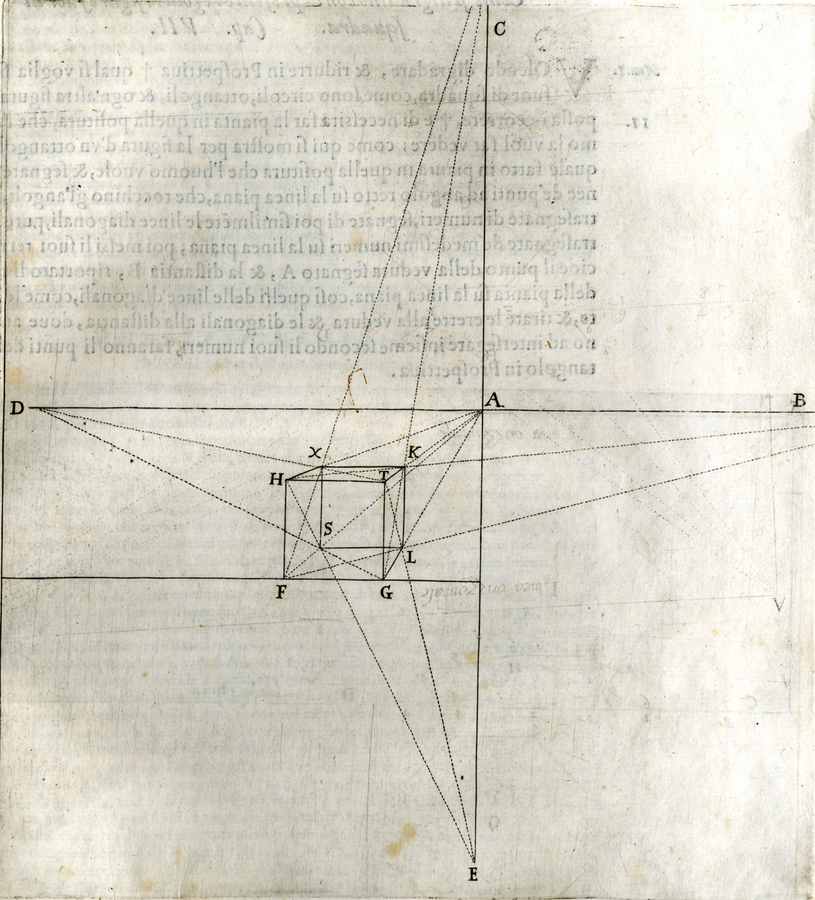
Fig. 7.7: Vignola’s illustration for his construction of a cube in perspective. It reveals how he applied the distance points D and B (though he did not include the latter point itself in his diagram) when he constructed the image of the cube’s bottom square, and how he let the images of the diagonals in the two vertical squares that are not parallel to the picture plane converge in the points E and C (again, he did not include the latter point) (Vignola 1583, 107; with kind permission of the Biblioteca Oliveriana, Pesaro)
Definition V
Perspective parallel lines are those that will meet at the horizontal point [a point on the horizon].
Definition VII
A distance point is that at which all the diagonals arrive.
Definition X
Principal parallel lines are those which will all converge at the principal point of perspective [principal vanishing point].
Definition XI
Secondary parallel lines are those which will be united at the horizontal line at their particular points apart from the principal point.3
Thus, Danti
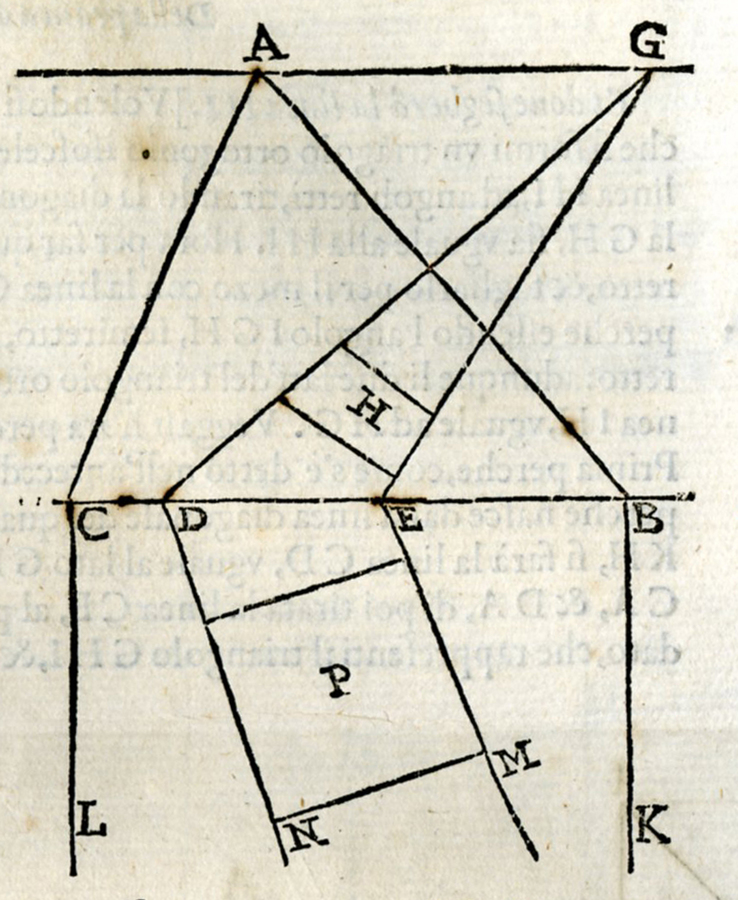
Fig. 7.8: Danti’s
In this he let one pair of the images of the parallel sides of the horizontal square P converge at the point G on the horizon whereas the two other sides do not converge at the direction of the horizon AG. He may, of course, have made a drawing error, but if so the diagram shows that it was not entirely clear to him that the images of parallel horizontal lines not parallel to the picture plane should meet on the horizon.
Benedetti
Summing up the Italian developments before Guidobaldo, it can be concluded that some convergence points were applied—but there was no mathematical understanding of their property.
7.3 Guidobaldo Changing the Foundation of Perspective
Guidobaldo was a man of independent means and spent much time studying at his estate in Montebaroccio near Urbino. Here he had contact with Commandino
My perspective is half asleep and half awake, because—to tell you the truth—I have so many engagements that I can scarcely breathe. For these matters I need to be free of all concerns. Still, I do want to finish it [...]. However, I have not yet discovered everything [...].4
By September, Guidobaldo thought it would be possible to finish his work during the winter and to have it published within a year (Galilei 1929-1939, vol. 10, 62)

Fig. 7.9: The title page of Guidobaldo’s epoch-making book on perspective. The sentence in the ribbon I interpret as “without deception we are deceived.”
Besides being busy with various obligations, it seems that Guidobaldo spent much time trying to understand what made perspective work as it did, or in other words investigating the foundation of the theory of perspective. We can even, to some extent, follow his path to the great insight in his printed work, because there he included some of his early results despite the fact that they had been made superfluous by his subsequent research. An illustrative example of this is his treatment of a general convergence rule for parallel line segments.
Guidobaldo started by looking at parallel horizontal line segments like BC, DE, and FG in Figure 7.10 in which A is the eye point and HKML the picture plane—which is not parallel to the parallel line segments.
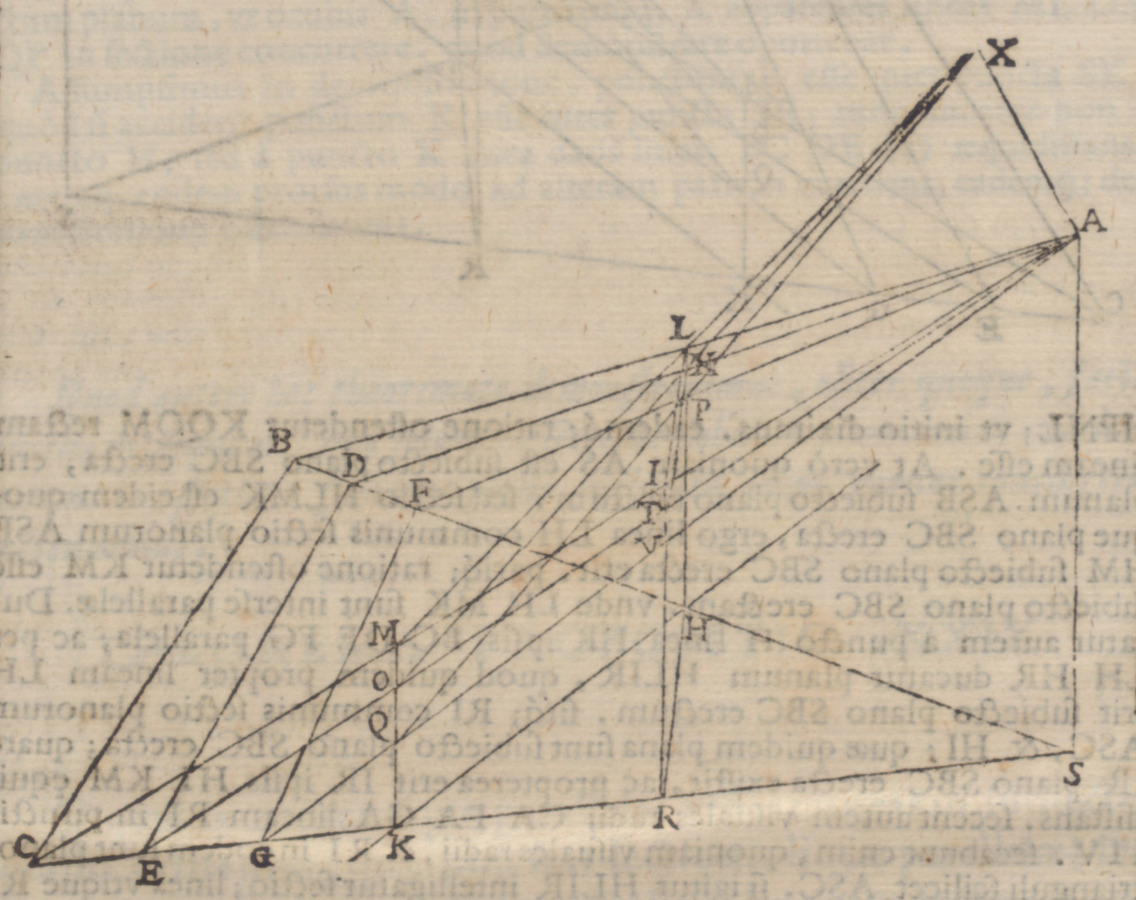
Fig. 7.10: Guidobaldo’s illustration for one of his proofs concerning a general vanishing point (Monte 1600, 35).
From reading Vignola
It is worth noting that in this first treatment of parallel line segments Guidobaldo related the convergence point X, which he called punctum concursus, to the images of the parallel lines and not to the lines themselves. This way of conceiving convergence points he shared with his predecessors, and it has very appropriately been described by Marchi
In his subsequent investigations Guidobaldo extrapolated from his result concerning the images of horizontal parallel line segments and in this process he seemed to get more and more insight ending up with a completely general result concerning the images of any set of parallel line segments that are not parallel to the picture plane, for which he gave a very elegant proof (Andersen 2007, 249)
Before describing the content of this theorem, I would like to return to my discussion of the introduction of a convergence point. As we saw, Guidobaldo first characterized it as the point in which the images of parallel lines—not parallel to the picture plane—converge, and gave it the name convergence point. However, in his last proof for the general theorem he introduced the convergence point differently. First, he considered a situation in which there is given a picture plane
 , an eye point O, and a line AB cutting the picture plane in A (Figure 7.11 the lettering is mine). Then he introduced the point V as the point of intersection of the plane
, an eye point O, and a line AB cutting the picture plane in A (Figure 7.11 the lettering is mine). Then he introduced the point V as the point of intersection of the plane
 and the line through the eye point O parallel to the line AB (Monte 1600, 43; cf. Andersen 2007, 248)
and the line through the eye point O parallel to the line AB (Monte 1600, 43; cf. Andersen 2007, 248)
How can we prove that this vanishing point is the same as the previously considered convergence point? The answer is: with the help of the main theorem. It is hence the right place to present this theorem. In fact, the main theorem is very easy to formulate, as it states that the image of a line intersecting the picture plane like AB in Figure 7.11 is determined by its point of intersection A and its vanishing point V. Perhaps, this result does not seem very impressive, but it turned out to be almost revolutionary in the mathematical theory of perspective.
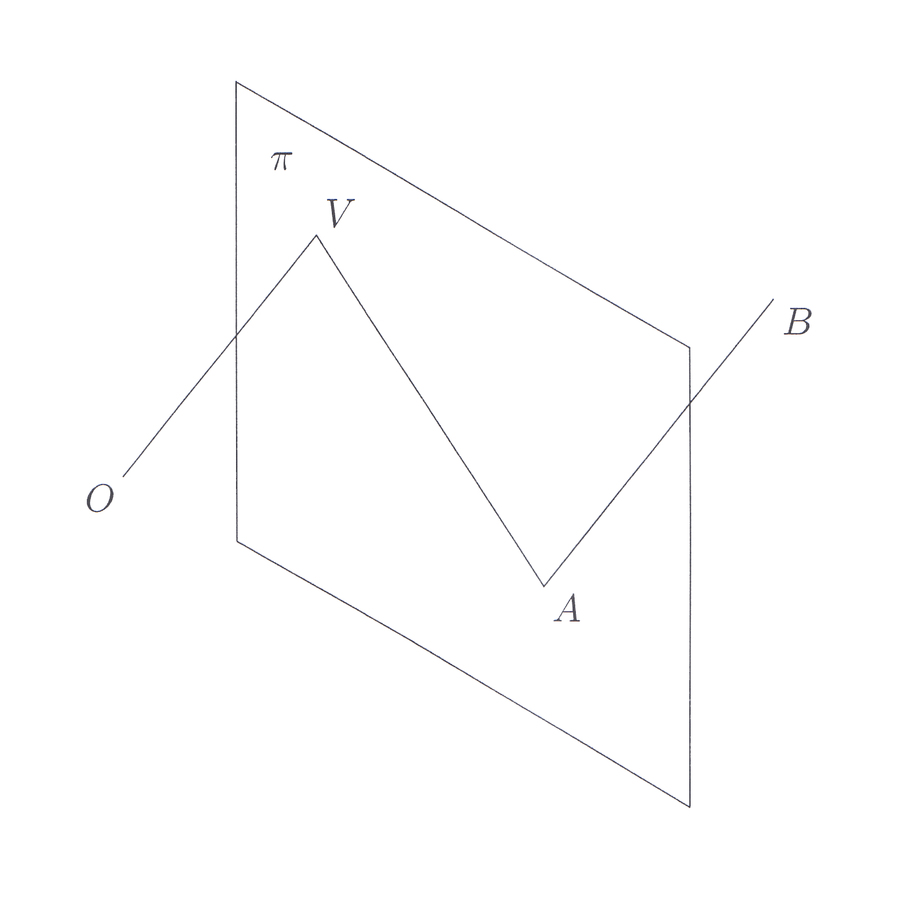
Fig. 7.11: Diagram to illustrate Guidobaldo’s general determination of the image of the line AB.
It is not immediately clear how we get from the result that the image of the line AB lies on the line AV to the relation between a convergence point and a vanishing point. However, if we consider a second line segment CD parallel to AB (Figure 7.12), we can conclude from the main theorem that this line segment has an image that is determined by the point C and the point in which the line through the eye point O parallel to CD cuts the picture plane
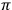 . Since AB and CD are parallel, the latter line is also OV, thus the image of CD lies on the line CV, implying that the images of the two parallel lines AB and CD meet or converge at the point V. And for any other line parallel to AB and CD, the same argument shows that its image also passes through V. Hence the point V is indeed a convergence point.
. Since AB and CD are parallel, the latter line is also OV, thus the image of CD lies on the line CV, implying that the images of the two parallel lines AB and CD meet or converge at the point V. And for any other line parallel to AB and CD, the same argument shows that its image also passes through V. Hence the point V is indeed a convergence point.
Fig. 7.12: Diagram to illustrate that the two parallel lines AB and CD have the common vanishing point V.
I mentioned that Guidobaldo’s proof of the main theorem was very elegant; it was also short and did not need any greater geometrical insight than the one he had inherited from classical Greek mathematics. Thus, it was not Guidobaldo’s proof that gave rise to his new insight; rather it was the process of investigation that made him focus on convergence points and that led him to the concept of a general vanishing point—although he kept the name convergence point. This was really a crucial step in the history of the mathematical theory of perspective. With some simplification, it can be claimed that all further developments of this theory were a generalization of Guidobaldo’s idea of a vanishing point for any set of parallel lines that are not parallel to the picture plane and of the main theorem of perspective.
As I noted in the introduction, Guidobaldo’s result was more fundamental and had greater potential than he himself perhaps realized. And he was not the only one not to see how fundamental an insight he had reached. In fact, although the main theorem also constituted the primary theoretical tool for his successors, it took more than a hundred years before this was made explicit. The person to do so was Taylor
7.4 Guidobaldo’s Main theorem and Perspective Constructions
Guidobaldo’s new theory made it easy to conclude that Alberti
To be able to make perspective constructions of objects it is sufficient to be able to construct the images of given points. However, all Guidobaldo’s predecessors had presented construction of polygons, and Guidobaldo kept to this practice. Still, the methods he created were in principle point-wise constructions. Thus, from the image of a line, Guidobaldo turned to determining the image of a given point; he did this by constructing the images of two lines passing through the given point. He was so greatly taken by the possibility his main theorem offered him in choosing a pair of lines through a given point that he presented no less than twenty-three different methods of constructing the image of a point (Monte 1600, 61–104).
7.5 Guidobaldo’s Other Contributions to Perspective
Apart from solving the problem of understanding the geometry behind perspective constructions, Guidobaldo touched upon a number of new themes in his Perspectivae libri sex; I briefly describe the three I find the most interesting, namely:
How to perform perspective constructions in other picture planes than vertical ones, such as oblique and curved planes.
How can we from perspective compositions gain knowledge about the original configuration?
A subject I call direct constructions in the picture plane, whereby I mean constructions that are performed directly in the picture plane without involving auxiliary drawings such as a plan.
In giving up the requirement that a picture plane should be vertical, Guidobaldo started by explaining how to construct images in an oblique picture plane (Monte 1600, 136–151). His treatment of this subject was based on the main theorem which he had formulated so generally that it also includes oblique planes. He continued by studying constructions in rather spectacular screens which were composed of more surfaces, some of which could be curved. In one of his examples he went so far as to consider a picture plane formed by a surface combined of a cylinder, a sphere and a cone (Monte 1600, 164). Working with curved surfaces can become very complicated, but Guidobaldo kept to fairly simple examples.
The theme of getting information from a perspective drawing has become known as inverse problems of perspective. In general such problems have more mathematical than practical relevance since a perspective projection is chosen when one wants to give a visual impression of how an object looks. If one wants to convey a precise information about the shape of an object, another representation than a perspectival projection is chosen, for instance a parallel projection or a plan and an elevation.6 There is, however one inverse problem of perspective that does have some practical interest, namely the following. Where should a person standing in front of a perspective image place his or her eye to properly perceive the scene created by the artist?
From a mathematical point of view, answering this question means reconstructing the eye point that the artist used for making his perspective drawing. The general problem of finding the eye point for a perspective composition is indeterminate, unless some information is given or some assumptions made. This may typically involve assuming that a tiled floor is the image of a floor with square tiles. However, rather than being inspired by practical questions or driven by a wish to gain mathematical insights, Guidobaldo seems to have taken up inverse problems because he wanted to use their solutions as auxiliary results for perspective constructions (Andersen 2007, 261)
Though Guidobaldo himself did not do much about inverse problems of perspective, he may have inspired several of the leading mathematicians in the field of geometrical perspective, including Stevin
With respect to direct constructions Guidobaldo treated two examples in each of which he showed how one of the basic Euclidean
7.6 Guidobaldo’s Influence on the Academic Approach
to Perspective
Although Guidobaldo’s accomplishment in the theory of perspective really deserves to be known, he himself seems to have been unable to pass on the message that his theory was helpful for those who wanted to understand the operations performed in perspective constructions. In September 1593 he wrote to Galileo
Fig. 7.13: In this drawing Johan Vredeman de Vries
Jean Étienne Montucla
Moreover, the work by Guidobaldo suffers from the usual fault of its time; the matter it presents in a multitude of theorems could have been expressed far more neatly in fewer pages.7
While I agree with Montucla’s
Considering the effort it takes to read Perspectivae libri sex, I suspect that the number of people who studied the work thoroughly is small; among those who have I would count Stevin
Throughout this chapter I have concentrated on Guidobaldo’s contributions to the theory of perspective, but when drawing the discussion to its end it seems appropriate to touch upon what his work meant to the practice of perspective. One of his successors, Claude François Milliet Dechales
The theory of this work is solid and geometrical, yet the method is somewhat on the difficult side. As a result, no one could learn perspective from this book alone; because it appears that it does not go sufficiently down into its practice. However, if one is moderately versed in perspective, one can gain much enlightenment from the book.8
Dechales
7.7 Conclusion
In short, it can be concluded that an interest among Italian mathematicians in the latter half of the sixteenth century inspired Guidobaldo to take up perspective. He inherited the idea that not only orthogonals and diagonals have vanishing points, and through a gradual process, he came to realize the importance of the main theorem of perspective. His achievements were extremely important for the development of the mathematical theory of perspective and had some consequences for its practice. However, it was his results rather than his presentation that inspired his successors.
Let me add that Guidobaldo closed one era and opened another in the history of the mathematical theory of perspective in the sense that he provided the geometrical explanations behind perspective constructions and gave his successors inspiration to continue along his line. Thus, there is the following trajectory of inspiration (Andersen 2007, 717)
The story about the development of the mathematical theory of perspective ends with Lambert because he left no important questions about how to project three-dimensional figures upon a plane surface unanswered. Lambert’s approach to perspective was to perform all constructions directly in the picture plane; in doing so he fully elaborated one of Guidobaldo’s contributions to perspective.
Acknowledgement
I am extremely thankful to Henk Bos for having commented upon this paper and not least for having drawn the Figures 7.1–5, 7.11 and 7.12.
References
Aguilon, F. (1613). De scenographice. In: Opticorum libri sex Antwerpen: Officina Plantiniana 637-681.
Alberti, L. B. (1972). On painting and on sculpture. The latin texts of De pictura and De statua. London: Phaidon.
Andersen, K. (2007). The Geometry of an Art: the History of the Mathematical Theory of Perspective from Alberti to Monge. New York: Springer.
Andersen, K., E. Gamba (2008). Monte, Guidobaldo, Marchese Del. In: New Dictionary of Scientific Biography Ed. by N. Koertge. Detroit: Scribners' Sons 174-178
Benedetti, G. B. (1585). Diversarum speculationum mathematicarum, et physicarum liber: quarum seriem sequens pagina indicabit. Torino: Bevilaqua.
Commandino, F. (1558). Federici Commandini urbinatis in Planisphaerium Ptolemaei commentarius. Venezia: Aldo Manuzio.
De Vries, Johann V. (1604-1605). Perspective: das ist die weit beruehmte Khunst. Leiden: Hondius.
Dechales, C. F. M. (1690). Cursus seu mundus mathematicus. Lyon: Posuel Rigaud.
Galilei, G. (1929-1939). Le opere di Galileo Galilei. Firenze: Barbèra.
Marchi, P. (1998) L'invenzione del punto di fuga nell'opera prospettica di Guidobaldo dal Monte. mathesis. Università degli studi di Pisa
Marolois, S. (1614). La perspective contenant la theorie et la pratique. Den Haag: H. Hondius.
Monte, Guidobaldo del (1600). Perspectivae libri sex. Pesaro: Girolamo Concordia.
Montucla, J. E. (1758). Histoire des mathématiques. Paris: Jombert.
Piero, della Francesca (1942). De prospectiva pingendi. Firenze: Sansoni.
Rose, P. L. (1974). Monte, Guidobaldo, Marchese Del. In: Dictionary of Scientific Biography Ed. by C. C. Gillispie. New York: Scribners' Sons 487-489
Sinisgalli, R. (1978). Per la storia della prospettiva (1405-1605). Il contributo di Simon Stevin allo sviluppo scientifico della prospettiva artificiale ed i suoi precedenti storici. Roma: L'Erma di Bretschneider.
Stevin, S. (1605a). De optica. In: Hypomnemata mathematica a Simone Stevino. Tomus tertius Leiden: Ex Officina Ioannis Patii
- (1605b). Des perspectives. In: Mémoires mathématiques par Simon Stevin. Livre trois Leiden: Paedts Iacobsz
- (1605c). Van de verschaeuwing. Eerste bouck der deursichtighe. In: Wisconstighe Ghedachtnissen Leiden
Taylor, B. (1715). Linear Perspective: or, a New Method of Representing justly all Manner of Object. London.
- (1719). New Principles of Linear Perspective: or the Art of Designing on a Plane the Representations of all Sorts of Objects, in a more General and Simple Method than has been done before. London.
Vignola, J. Barozzi (1583). Le due regole della prospettiva pratica di M. Iacomo Barozzi da Vignola, con i comentarij del R.P.M. Egnatio Danti dell'ordine de predicatori, matematico dello studio di Bologna. Roma: Francesco Zannetti.
Footnotes
Alberti himself, however, seems to have wondered about this correctness, because he wrote that he had involved some geometrical explanations when presenting his construction to some of his friends (Alberti 1972, §23).
All authors before Simon Stevin (whose work on perspective appeared in 1605, see Stevin 1605a, 1605b and 1605c; Sinisgalli 1978, 167–344) introduced their construction methods as constructions of the perspective images of polygons—in most cases of squares—situated in a given horizontal reference plane. However, the constructions could also be used to construct the image of a given point in the reference plane.
Definitione quinta: Linee parallele prospettive sono quelle, ché si vanno a congiugnere nel punto orizontale. Definitione settima: Punto della distanza è quello, dove arrivano tutte le linee diagonali. Definitione decima: Linee parallele principali son[o] quelle, che vanno a concorrere tutte insieme nel punto principale della Prospettiva. Definitione XI: Linee parallele secondarie sono quelle, che vanno ad unirsi fuor del punto principale nella linea orizontale, alli loro punti particolari (Vignola 1583, 4–5).
“La mia Prospettiva mezzo dorme e mezzo vegghia, ché, a dir il vero, io ho tante le occupationi, che non mi lasciano respirare; e per queste cose bisognarebbe esser libero da ogni fastidio: pur la voglio finir [...]; ma non ho ancor trovato ogni cosa [...]” (Galilei 1929-1939, vol. XX, 54).
For details see (Andersen 2007, 247; Marchi 1998, 94–103).
In the mid-nineteenth century the theory of inverse perspective underwent a revival and was further developed in connection with photographic surveying.
“Au reste, l’ouvrage de Guido-Ubaldi a le défaut ordinaire de ceux de son temps; ce qu’on y trouve exposé en une multitude de propositions, pouvoit être dit avec plus de netteté en peu de pages” (Montucla 1758, vol.1, 636).
“Doctrina hujus operis solida est & geometrica, tamen methodus paulo difficilior; ita ut nullus in eo solo libro possit perspectivam addiscere, videtur enim non satis ad praxin descendisse, qui tamen in perspectiva mediocriter esset versatus posset ex eo multum lucis haurire,” in (Dechales 1690, 68).
