11.1 Rischi e competenze
Tra la fine del XVI e l’inizio del XVII secolo manoscritti e testi a stampa
presentano i temi e le contraddizioni che occuperanno il dibattito sui
rapporti tra meccanica e architettura sino al Novecento. Nuovi saperi prendono
forma e nell’arco di pochi anni si assiste ad un cambiamento di prospettiva
che fa apparire improvvisamente superate opere che sino a poco prima
sembravano di frontiera. La distanza che separa la prima edizione latina (e
la seconda italiana) del commento di
Daniele Barbaro
11.2 Muri, macchine, stadere
Nel campo intermedio della meccanica applicata all’architettura
l’accelerazione sopra segnalata assume dunque connotati più sfumati. La
difficoltà di leggere la costruzione architettonica in termini meccanici
risulta evidente in tutta la letteratura dell’epoca. Già i manoscritti di
Leonardo da Vinci
Sulla base di un sapiente saper fare si stavano infatti realizzando
alcune tra le più notevoli costruzioni architettoniche del Rinascimento,
particolarmente interessanti dal punto di vista statico-costruttivo. Si pensi
alla (ri)costruzione del ponte Santa Trinita (1567–1570) a
Firenze, del ponte di Rialto a Venezia (1588–1591), della Fleischbrücke (1596–1598) a Nürnberg, oppure alla costruzione della cupola di S. Pietro3 a Roma (serrata nel 1589). Opere legate a lunghi
dibattiti, a discussioni dotte, a considerazioni nelle quali gli interrogativi
“meccanici” non potevano non avere un peso rilevante e che nel contempo
richiedevano risposte operative affidabili, concrete, tempestive. È quello
che cerca di offrire, ad esempio, Giovanni Antonio Rusconi
Altri autori, ai quali si devono pregevoli scritti
di architettura, non offrono indicazioni più approfondite e le
considerazioni sulla stabilità e la resistenza della fabbrica solitamente
non superano la soglia del semplice cenno. Nel caso
delle cupole descritte da Scamozzi
A questo problema storico si aggiunge un problema storiografico. Le fonti che
consentirebbero di stabilire una connessione convincente tra conoscenze
meccaniche e costruzione architettonica sono ancora oggi in gran parte da
studiare, in molti casi, probabilmente, da scoprire (o riscoprire). Se i
più tardi Discorsi e dimostrazioni matematiche di Galileo
In realtà la dissertazione sull’Inferno dice ben poco sulla resistentia solidorum e sulla meccanica delle strutture, quanto scrive Galileo
Ma lasciamo stare l’architettura, e veggiamo se tal fabbrica può reggersi, che, al parer mio, troveremo non potere; perché, ponendo esso che il burrato si alzi su con le sponde equidistanti tra di loro, si troveranno le parti superiori prive di sostegno che le regga, il che essendo, indubitatamente rovineranno: perciò che, essendo che le cose gravi, cadendo, vanno per una linea che dirittamente al centro le conduce, se in essa linea non trovano chi le impedisca e sostenga, rovinano e caggiono. Se dunque sopra questa buca puntano e si sostengono le altre rocce, è necessario che le mura che le deono sostenere non siano fuori del perpendicolo che tende al centro. Questo inconveniente non è nell’architettura del Manetti.
Più avanti Galileo
Qui ci potrebbe essere opposto che né l’Inferno si deve credere esser così grande come il Manetti lo pone; essendo che, sì come alcuni hanno sospettato, non par possibile che la volta che l’Inferno ricuopre, rimanendo sì sottile quant’è di necessità se l’Inferno tanto si alza, si possa reggere, e non precipiti e profondi in esso Inferno; e massime, oltre al rimanere non più grossa dell’ottava parte del semidiametro, che sono miglia 405 incirca, essendovi ancora da levarne per lo spazio della grotta degli sciagurati, ed essendoci molte gran profondità di mari. Al che facilmente si risponde, che tal grossezza è suffizientissima: perciò che, presa una volta piccola, fabricata con quella ragione, se arà di arco 30 braccia, gli rimarranno per la grossezza braccia 4 in circa, la quale non solo è bastante, ma quando a 30 braccia di arco se gli desse un sol braccio, e forse, non che 4, basteria a sostenersi; onde, sapendo noi che pochissime miglia, anzi che meno di un sol miglio, si profondano i mari, se creder doviamo a i più periti marinari, e potendo assegnare quante miglia ci pare per la grotta de gli sciagurati, non essendogli data dal Poeta determinata misura, quando ancora ponessimo tra questa e la profondità de i mari importare 100 miglia, nulla di meno rimarrà detta volta grossissima, e più assai che non è necessario per sostenersi.
Alcuni studiosi hanno cercato di assegnare un particolare significato a queste
pagine giovanili10, ma le riflessioni presentate da Galileo
In precedenza altri autori avevano offerto spunti sparsi sull’argomento, che
avrebbero potuto aiutare a trovare una soluzione, ma che non vennero raccolti
e messi a frutto sino all’inizio del XVII secolo. I riferimenti classici sui
quali meritava indagare e che poi si riveleranno decisivi per la moderna
impostazione dei problemi di meccanica strutturale erano le opere di cinque
autori, intensamente studiati e commentati nel corso del Rinascimento:
Aristotele
La celebre trasportatione realizzata da Domenico Fontana
Anche Pigafetta
Intorno al trasporto dell’obelisco vaticano si ritrovano quindi alcuni dei
migliori spiriti dell’epoca e quel cantiere, messo in opera pochi anni prima
della cupola di S. Pietro e a poca distanza da essa, sembra rappresentare un
ideale terreno sperimentale per chi si stava cimentando con i principi della
nuova scienza meccanica. Il cantiere guidato da Domenico Fontana
Le fonti antiche prese a riferimento provengono dal mondo della meccanica e da
quello dell’architettura, come dimostra, ad esempio, il caso della corona
d’oro di Gerone, descritto da Vitruvio
11.3 L’architettura come cantiere di idee
Nell’ambiente urbinate raccolto intorno a Federico Commandino nessuno poteva
considerarsi estraneo ai temi sopra evocati, pur non avendoli coltivati nel
dettaglio: sia per il comune interesse per le opere degli autori ricordati,
sia per le precise connessioni col mondo dell’architettura. L’ars
aedificandi era presente in casa Commandino grazie al padre, che si era
occupato delle nuove fortificazioni della città di Urbino, mentre
Guidobaldo si era interessato a più riprese di temi analoghi, sollecitato
da amici e concittadini:20
Il confronto serrato con i trentacinque Problemi meccanici (da Baldi
Dal punto di vista teorico-letterario la passione per l’architettura è testimoniata da due
opere magistrali, molto apprezzate all’epoca della pubblicazione e considerate
esemplari anche nei secoli successivi: il De verborum Vitruvianorum
significatione (Baldi 1612)
ed ancorché si trovasse allora lontano di quella città, nondimeno coll’aiuto e della pianta, che egli stesso aveva dapprima cavata, e della sua maravigliosa memoria, la fece con tale esattezza, quale fatta l’avrebbe se si fusse ritrovato in Urbino: fatica riputata utilissima nella professione dell’architettura, imperciocché per essere assai difficile il sito, ove quel palagio è fabbricato, molto riesce malagevole il poter riconoscersi dalla semplice pianta la sua intera bellezza.
Le caratteristiche tecniche di quel palazzo-mondo sono meticolosamente descritte,
dalle fondamenta alla coperture, soffermandosi sulle proprietà dei
materiali, sulle ingegnose soluzioni progettuali, sugli accorgimenti che
avevano saputo render splendida e armoniosa “una macchina
così grande,” conciliando sapientemente materia
e forma (Baldi 1724, 69)
Lo scavo nei testi meccanici e nei testi architettonici era dunque avvenuto,
nel suo caso, secondo due solchi paralleli, che alla fine confluirono in un
comune campo di ricerca. Per questa ragione Vitruvio
La riflessione di Baldi
Occorre ricordare che questo cambio di prospettiva rappresenterà un continuo rovello per la
nascente rational mechanics. Il tema del corpo rigido posto in
relazione alle applicazioni del principio della leva sarà efficacemente
sottolineato da Pierre-Simon Girard
Si dans la théorie de la statique il est permis de regarder les leviers au moyen desquels les mobiles agissent les uns sur les autres comme doués d’une inflexibilité parfaite, cette supposition cesse d’être admissible dans l’application de cette science au calcul des machines, puisque la nature n’a créé aucune substance dont les parties intégrantes ne puissent être séparées les unes des autres par l’action d’un certain effort. Il y a donc deux espèce d’équilibre à considérer dans le levier, et dans les machines qui s’y rapportent; l’un existe entre les efforts opposés qui se contrebalancent, l’autre entre une certaine fonction de ces efforts et la cohérence des parties dont les machines sont composées. On peut assigner rigoureusement les conditions du premier, mais celles du second ne sont assignables que par approximation.
Più in generale si tratta di un tema che configura la
differenza epistemologica tra equazioni generali dell’equilibrio ed equazioni
costitutive. Ancora nell’Ottocento persino la teoria dell’elasticità, che
di questi studi è l’erede diretta, avrà difficoltà ad imporsi
proprio a causa di queste caratteristiche. Si pensi alle obiezioni rivolte da
Louis Poinsot
Lo scarto concettuale proposto da Baldi
Per Baldi
Credo che gli uomini abbiano appreso a costruir l’arco in questo modo. Accortisi che due travi con le estremità superiori unite potevano essere fissate in basso, nel luogo in cui le loro basi erano divaricate, in modo tale che, reciprocamente collegate ed equilibrandosi con identico peso, si reggessero tra loro, la scoperta ebbe successo, e con questa tecnica si cominciarono ad impiegare negli edifici i tetti a displuvio. In seguito, probabilmente, avendo intenzione di coprire con quelli un maggiore spazio e ciò non potendo per essere le travi troppo corte, sistemarono una trave intermedia nel punto più alto, alla sommità dei tronchi, facendone risultare a un dipresso la figura di una P greca (); e l’elemento aggiunto chiamarono probabilmente concio. Anche questa invenzione ebbe fortuna, anzi i conci vennero moltiplicandosi, giungendo a costituire una sorta di arco, la cui forma piacque. Si pensò così di trasferire questa tecnica alle opere di pietra, e coll’aggiunta di altri conci pervennero a fabbricare un arco intero.34
L’elegante ricostruzione storico-genetica diventa illuminante
indizio meccanico e come tale non deve essere sfuggita all’occhio attento
dell’abate di Guastalla. Senza fare esplicito riferimento ad Alberti
11.4 Idee allo stato nascente
Non è possibile in questa sede approfondire ulteriormente il tema
meccanica-architettura al tempo di Guidobaldo35, è
però utile indicare alcune ricerche che meriterebbe sviluppare. È
stata ricordata la trasportatione dell’obelisco vaticano guidata da
Domenico Fontana
È proprio in quel periodo che Baldi
A quel punto occorrerà probabilmente rileggere con attenzione le opere di
Benedetti, Clavio, Guidobaldo e Galileo
Riferimenti
Agrippa, C. (1583). Trattato di Camillo Agrippa Milanese di trasportar la guglia in su la Piazza di San Pietro. Roma: Francesco Zanetti.
Alberti, L. B. (1485). De re aedificatoria. Firenze: Nicolò di Lorenzo Alemanno.
- (1966). L'Architettura [De re Aedificatoria]. Testo latino e traduzione a cura di Giovanni Orlandi. Introduzione e note di Paolo Portoghesi. Milano: Il Polifilo.
Aristotele (1936). Mechanical Problems. In: Minor Works Cambridge, Mass.: Harvard University Press
- (2000). Problemi meccanici. Introduzione, testo greco, traduzione italiana. Catanzaro: Rubbettino.
Baldi, B. (1590). Descrittione del Palazzo ducale di Urbino. In: Versi e Prose Venezia: Francesco de' Franceschi Senese 503-573
- (1612). De verborum Vitruvianorum significatione, sive perpetuus in M. Vitruvium Pollionem commentarius. Augsburg: ad insigne Pinus.
- (1621). In mechanica Aristotelis problemata exercitationes: adiecta succinta narratione de autoris vita et scriptis. Mainz: Typis & Sumptibus Vi- duae Ioannis Albini.
- (1724). Descrizione del Palazzo Ducale d'Urbino. In: Memorie Concernenti la Città di Urbino Roma: Salvioni
- (1998). Le vite de'matematici. Edizione annotata e commentata della parte medievale e rinascimentale. Milano: Franco Angeli.
- (2010). In mechanica Aristotelis problemata exercitationes, Vol. 1: Testo latino riveduto e corretto con traduzione italiana a fronte. Milano: Franco Angeli.
Barbaro, D. (1556). I dieci libri dell'Architettura di M. Vitruvio tradutti e commentati da Monsignor Barbaro, eletto Patriarca d'Aquileggia. Venezia: Marcolini.
- (1567a). I dieci libri dell'architettura di M. Vitruvio tradutti e commentati da Monsignor Barbaro, eletto Patriarca d'Aquileggia. Venezia: F. de' Franceschi & G. Chrieger.
- (1567b). M. Vitruvii Pollionis de architectura libri decem, cum commentariis Danielis Barbari. Venezia: Franciscum Franciscium Senensem, & Ioan. Crugher Germanum.
Becchi, A. (2004). Q. XVI. Leonardo, Galileo e il caso Baldi: Magonza, 26 marzo 1621. Venezia: Marsilio.
- (2009). Uno e trino. Impronte stravaganti di un testimone postumo (1621). In: Saggi di letteratura architettonica, da Vitruvio a Winckelmann Firenze: Olschki 19-35
Bedon, A. (1983). Il `Vitruvio' di Giovan Antonio Rusconi. Ricerche di Storia dell'Arte 19: 84-90
- (1996). Giovan Antonio Rusconi: illustratore di Vitruvio, artista, ingegnere, architetto. In: G. A. Rusconi, dell'architettura (1590) Vicenza: Centro Internazionale di Studi di Architettura Andrea Palladio IX-XXII
Belluzzi, A., G. Belli (2003). Il ponte a Santa Trinita. Firenze: Polistampa.
Bernini, D. (2002). Bernardino Baldi e il Palazzo Ducale di Urbino. Accademia Raffaello. Atti e Studi I: 58-79
Bertrand, J. (1873). Notice sur Louis Poinsot. In: Éléments de statique Ed. by L. Poinsot. Paris: Gauthier-Villars 9-28
Biener, Z. (2004). Galileo's First New Science: The Science of Matter. Perspectives on Science 12: 262-287
Calabi, D., P. Morachiello (1987). Rialto: le fabbriche e il ponte. Torino: Einaudi.
Calegari, G. (2004). Palazzo Mamiani della Rovere: indagini e scoperte. In: Palazzo Gradari già Palazzo Mamiani Della Rovere. Indagini e scoperte dopo il restauro D. Trebbi, S. Bruscia, A. Nori, G. Calegari Ancona: Futura Officine Grafiche 113-140
Campori, G. (1855). Gli artisti italiani e stranieri negli Stati Estensi. Modena: Tip. della R. D. Camera.
Carugo, A. (1979). Gli obelischi e le macchine nel Rinascimento. In: D. Fontana, Della trasportatione dell'Obelisco Vaticano Milano: Il Polifilo
Crescimbeni, G. M. (2001). La vita di Bernardino Baldi Abate di Guastalla. Urbino: QuattroVenti.
Daniello, A. (1568). Dante con l'espositione di M. Bernardino Daniello da Lucca, sopra la sua Comedia dell'Inferno, del Purgatorio, & del Paradiso; nuouamente stampato & posto in luce[…]. Venezia: Pietro da Fino.
Duhem, P. (1905-1906). Les origines de la statique. Paris: Hermann.
- (1906-1913). Études sur Léonard de Vinci: Ceux qu'il a lus et ceux qui l'ont lu. Paris: Hermann.
Engel, H. (2006). Dantes Inferno. Zur Geschichte der Höllenvermessung und des Höllentrichtermotivs. München/Berlin: Deutscher Kunstverlag.
Fontana, D. (1590). Della trasportatione dell'Obelisco Vaticano […]. Roma: Domenico Basa.
Galilei, G. (1638). Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla mecanica et i movimenti locali. Leiden: Elsevirii.
- (1958). Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti alla mecanica ed i movimenti locali. Torino: Boringhieri.
- (1968). G. Galilei, Le opere. Florence: Barbera.
Galilei, Galileo (2011). Due lezioni all'Accademia fiorentina circa la figura, sito e grandezza dell'Inferno di Dante. Livorno: Sillabe.
Gallaccini, T. (2003). Perigonia, o vero degli angoli. Siena: Accademia delle Scienze di Siena detta de' Fisiocritici.
Galluzzi, P. (2011). Tra atomi e indivisibili. La materia ambigua di Galileo. Firenze: Olschki.
Giambullari, P. (1544). De'l sito, forma, e misure, dello Inferno di Dante. Firenze: Neri Dortelata.
- (1551). Lezzioni di M. Pierfrancesco Giambullari, lette nella Accademia Fiorentina. Firenze: Lorenzo Torrentino.
Girard, P. S. (1798). Traité analytique de la résistance des solides et des solides d'Egale Résistance, auquel on a joint une suite de nouvelles expériences sur la force et l'elasticité spécifiques des bois de chêne et de sapin. Paris: Didot.
Giusti, E. (1990). Galileo e le leggi del moto. In: G. Galilei, Discorsi e dimostrazioni matematiche intorno a due nuove scienze attinenti alla mecanica ed i movimenti locali Torino: Einaudi
Hevelius, J. (1673). Machinae coelestis pars prior: organographiam, sive instrumentorum astronomicorum omnium, quibus auctor hactenus sidera rimatus, ac dimensus est, accuratam delineationem et descriptionem exhibens. Danzig: Auctoris typis, sumptibus, imprimebat Simon Reiniger.
Hochmann, M. (1987). La collection de Giacomo Contarini. Mélanges de l'Ecole française de Rome. Moyen-Age, Temps modernes vol. 99(1): 447-489
Kaiser, C. (2005) Die Fleischbrücke in Nürnberg (1596-1598). Ph. D. Thesis. TU Cottbus
Lévy-Leblond, J. M. (2006). Galilée dans l'Enfer de Dante. In: La vitesse de l'ombre. Aux limites de la science Ed. by J. M. Lévy-Leblond. Paris: Éditions du Seuil 80-85
Lohr, C. H. (1974). Renaissance Latin Aristotle Commentaries: Authors A-B. Studies in the Renaissance 21: 228-289
- (1975). Renaissance Latin Aristotle Commentaries: Authors C. Renaissance Quarterly 28: 689-741
- (1976). Renaissance Latin Aristotle Commentaries: Authors D-F. Renaissance Quarterly 29: 714-745
- (1977). Renaissance Latin Aristotle Commentaries: Authors G-K. Renaissance Quarterly 30: 681-741
- (1978). Renaissance Latin Aristotle Commentaries: Authors L-M. Renaissance Quarterly 31: 532-603
- (1979). Renaissance Latin Aristotle Commentaries: Authors N-Ph. Renaissance Quarterly 32: 529-580
- (1980). Renaissance Latin Aristotle Commentaries: Authors Pi-Sm. Renaissance Quarterly 33: 623-734
- (1982). Renaissance Latin Aristotle Commentaries: Authors So-Z. Renaissance Quarterly 35: 164-256
Malke, L. S. (2000). Dantes Göttliche Komödie. Drucke und Illustrationen aus sechs Jahrhunderten. Berlin: Kunstbibliothek-Staatliche Museen Berlin.
Manno, A. (1987). Giulio Savorgnan: Machinatio e Ars Fortificatoria a Venezia. In: Cultura, scienze e tecniche nella Venezia del Cinquecento. Atti del convegno internazionale di studio `Giovan Battista Benedetti e il suo tempo' Venezia: Istituto Veneto di Scienze, Lettere ed Arti 227-245
Mercati, M. (1589). De gli obelischi di Roma. Roma: Domenico Basa.
Monte, Guidobaldo del (1577). Mechanicorum liber. Pesaro: Hieronymum Concordiam.
- (1581). Le mechaniche dell'illustriss. sig. Guido Ubaldo de' Marchesi del Monte: Tradotte in volgare dal sig. Filippo Pigafetta. Venezia: Francesco di Franceschi Sanese.
- (1588). In duos Archimedis aequeponderantium libros paraphrasis scholijs illustrata. Pesaro: Hieronymum Concordiam.
Narducci, E. (1886). Vite inedite di matematici italiani scritte da Bernardino Baldi e pubblicate da Enrico Narducci. Bullettino di bibliografia e di storia delle scienze matematiche e fisiche
Palladio, A. (1570). I quattro libri dell'architettura. Venezia: Dominico de' Franceschi.
Peterson, M. A. (2002). Galileo's Discovery of Scaling Laws. American Journal of Physics 70: 575-580
Piasentin, M. (1978-1979) Giovan Antonio Rusconi. mathesis. IUAV
Pigafetta, F. (1586). Discorso di M. Filippo Pigafetta d'intorno all'historia della Aguglia & alla ragione del muoverla. Roma: Bartolomeo Grassi.
Prado, H., J. B. Villalpando (1596-1605). In Ezechielem explanationes et apparatus urbis, ac templi hierosolymitani commentariis et imaginibus illustratus opus tribus tomiis distinctum. Roma: A. ZanettiA. Ciacconi.
Prinz, W. (1983). Informazione di Filippo Pigafetta al serenissimo di Toscana per una stanza da piantare lo studio di architettura militare. In: Gli Uffizi. Quattro secoli di una galleria P. Barocchi, G. Ragionieri Firenze: Olschki 343-353
- (1988). Dal modello al dipinto: macchine da guerra di Archimede alla fine del Cinquecento. In: Architettura militare nell'Europa del XVI secolo. Atti del convegno di studi, Firenze, 25-28 Novembre 1986 Firenze: Edizioni Periccioli, 1988 409-416
Raphael, R. (2008). Galileo's Discorsi and Mersenne's Nouvelles Pensées: Mersenne as a Reader of Galilean `Experience'. Nuncius: Journal of the History of Science 23: 7-36
Ronchini, A. (1873). Lettere di Bernardino Baldi cavate dagli autografi che sono a Parma nell'Archivio di Stato. Parma: R. Deputazione di Storia Patria..
Rose, P. L. (1974). Rediscovered Manuscripts of the “Vite de'matematici” and Mathematical Works by Bernardino Baldi. Rendiconti Sc. Fis. Mat. e Nat. dell'Accademia dei Lincei 56: 272-279
- (1975). The Italian Renaissance of Mathematics. Genève: Droz.
Rose, P. L., S. Drake (1971). The Pseudo-Aristotelian Questions of Mechanics in Renaissance Cultures. Studies in the Renaissance 18: 65-104
Ruberto, L. (1882). Studij su Bernardino Baldi. Bologna: Tipografia Fava e Garagnani.
Rusconi, G. A. (1590). Della architettura, con centosessanta figure dissegnate dal medesimo […]. Venezia: Gioliti.
Satzinger, G., S. Schütze (2008). Sankt Peter in Rom 1506-2006. Beiträge der internationalen Tagung vom 22.-25. Februar 2006 in Bonn. München: Hirmer.
Scamozzi, V. (1615). Dell'Idea della Architettura Universale. Venezia: presso l'Autore.
Serrai, A. (2002). Bernardino Baldi. La vita, le opere. La biblioteca. Milano: Edizioni Sylvestre Bonnard.
Settle, T. B. (2001). Experimental Sense in Galileo's Early Works and its Likely Sources. In: Largo campo di filosofare Ed. by J. Montesinos, C. Solís. La Orotava: Fundación Canaria Orotava de Historia de la Ciencia 831-849
- (2002). Dante, the Inferno and Galileo. In: Pictorial Means in Early Modern Engineering, 1400-1650 Ed. by W. Lefèvre. Berlin: Max-Planck-Institut für Wissenschaftsgeschichte 139-157
Strano, G. (2008). Il telescopio di Galileo. Lo strumento che ha cambiato il mondo. Firenze: Giunti.
Tartaglia, N. (1546). Quesiti et inventioni diverse. Venezia: Venturino Ruffinelli.
Tassora, R. (2001) Le Meditatiunculae de Rebus Mathematicis di Guidobaldo del Monte. Ph. D. thesis. Università di Bari
Tiepolo, M. F. (1985). Ambiente scientifico veneziano tra Cinque e Seicento. Testimonianze d'archivio (mostra documentaria, 27 Luglio-6 Ottobre 1985). Venezia: Tip. Helvetia.
Valleriani, M. (2010). Galileo Engineer. Dordrecht: Springer.
Ventrice, P. (1998). Architettura militare e ingegneria tra XVI e XVII Secolo a Venezia. In: Giambattista Aleotti e gli ingegneri del Rinascimento Ed. by A. Fiocca. Firenze: Olschki 309-330
Vitruvio, M. P. (1997). De architectura. Torino: Einaudi.
Waźbiński, Z. (1994). Il cardinale Francesco Maria del Monte, 1549-1626. Firenze: Olschki.
Zaccagnini, G. (1902). La vita e le opere edite e inedite di Bernardino Baldi. Modena: Forghieri.
- (1908). Bernardino Baldi nella vita e nelle opere. Pistoia: Tipo-litografica Toscana.
Zorzi, G. (1956-1957). Altre due perizie inedite per il restauro del Palazzo Ducale di Venezia dopo l'incendio del 20 dicembre 1577. Atti dell'Istituto Veneto di Scienze, Lettere ed Arti 115: 169-170
Note a piè pagina
Cfr. (Barbaro 1567a e 1567b). La prima edizione del commento di Barbaro era stata pubblicata nel 1556 (Barbaro 1556).
Uno dei più lunghi telescopi, costruito a Danzica su progetto di Hevelius, misurava quarantacinque metri. È raffigurato nell’opera (Hevelius 1673, Figg. AA e BB). Su questi e altri aspetti della storia del cannocchiale cfr. (Strano 2008). In quest’ultimo volume, nella sezione intitolata Riprodurre il telescopio di Galileo (pp. 58-61) curata da Jim e Rhoda Morris, si descrive la struttura del telescopio che Galileo donò a Cosimo II (datato 1610 ca.).
Cfr., ad esempio, per il ponte Santa Trinita (Belluzzi and Belli 2003), per il ponte di Rialto (Calabi and Morachiello 1987), per la Fleischbrücke (Kaiser 2005) e per la cupola di S. Pietro (Satzinger and Schütze 2008).
Zorzi chiarisce in nota questa espressione: “Nel dialetto veneto, ‘slamar’ significa, slittare, scivolare;” cfr. (Zorzi 1956-1957, 168, nota 8).
Su Rusconi vedi (Piasentin 1978-1979; Bedon 1983; 1996).
Cfr. (Tartaglia 1546, libro IX, Quesito XXXVIII, 126 v). Il Quesito corrisponde ad una lettera a Girolamo Cardano del 4 Agosto 1539. Rusconi viene citato anche in altri passi dell’opera di Tartaglia.
“Questa forza, & egualità della Volta à Cupola la potiamo conoscere anco con l’esperienza delle cose naturali, e specialmente dal vuovo; il quale per sua natura havendo un scorzo cosi sottile, e debole, niente di meno non è forza humana, che lo possi rompere, come disse anco Plinio; perche strignendolo per il capo, e punta, che dimostrano i Volti di mezo cerchio, ò apuntati, & i suoi lati quelli scemi, ò manco, che di mezo cerchio; come si può trarre anco da Alessandro Affrodiseo: e noi habbiamo fatto prova, che tre vuova fernate in piedi sù una tavola, conun poco di cera da ambi i capi, hanno sostenuto il peso d’un mortaio di metallo di più di 150. libre di peso” (Scamozzi 1615, Parte II, Libro VIII, 320).
G. Galilei, Due lezioni all’Accademia Fiorentina circa la figura, sito e grandezza dell’Inferno di Dante, in (Galilei 1968, vol. IX, 31-46 e 47-57), nuova ristampa dell’edizione nazionale curata da Antonio Favaro (1890–1909). Le due lezioni sono facilmente reperibili online, ad esempio nel sito http://www.liberliber.it. Per le analisi critiche cfr. (Settle 2001 e 2002; Lévy-Leblond 2006; Galilei 2011; Peterson 2002); quest’ultimo testo è disponibile in versione digitale in http://www.mtholyoke.edu/courses/mpeterso/galileo/scaling8.pdf. Le due lezioni sono state oggetto recentemente di alcune rappresentazioni teatrali e multimediali, cfr. Antonella D’Aloisio, Varcare la soglia dell’Inferno. Architetture, proporzioni matematiche, immagini simboliche, virtuali e digitali delle “Due lezioni all’Accademia Fiorentina circa la figura, sito e grandezza dell’Inferno di Dante” di Galileo Galilei (1588) e di “Galileo all’Inferno” di Studio Azzurro (2006-2008), pubblicato il 19 giugno 2009 nel sito “Margine, Soglia, Confine, Limite,” http://solima.media.unisi.it/interventi.htm.
Peterson scrive con una certa enfasi (Peterson 2002, pagina 2 del testo online): “I will show that the key to much of what is strange in Two New Sciences is to be found in two rather neglected early lectures given by Galileo on the shape, location, and size of Dante’s Inferno.”
Cfr. (Giambullari 1551), vedi anche (Giambullari 1544; Daniello 1568). Su questi temi e sulla relativa iconografia cfr., tra gli altri, (Malke 2000; Engel 2006).
G. Galilei, Lettera ad Antoine de Ville, Arcetri, Marzo 1635. Cfr. (Galilei 1968, vol. XVI, 196). Fulgenzio Micanzio descrive la personalità di Antoine de Ville in una lettera a Galileo del 24 Febbraio 1635. Cfr. (Galilei 1968, vol. XVI, 217-218): “Questo è un gentill’huomo Francese, ingegnero qui, e, per quello posso conoscere, molto intelligente non solo nelle mecaniche, ma in tutte le scienze mathematiche et prattico ne’ buoni authori, ma, come quelli che sanno, ingenuo.”
F. Pigafetta, lettera dedicatoria a Giulio Savorgnano, posta in apertura dell’opera Guidobaldo del Monte, Le mechaniche (...) tradotte in volgare dal Sig. Filippo Pigafetta (Monte 1581, carta a2v). Nella Biblioteca Ambrosiana sono conservati numerosi manoscritti di Filippo Pigafetta, ad esempio gli appunti “Cose raccolte ad Osoppo da Ragionamenti fatti col Co. Giulio Savorgnano” (Cod. R. 125. Sup). Su Filippo e, in generale, sulla famiglia Pigafetta cfr. il Progetto Pigafetta della Biblioteca Civica Bertoliana di Vicenza (http://www.bibliotecabertoliana.it/pigafetta/pigafetta.htm).
Su Savorgnan cfr., ad esempio, (Manno 1987; Ventrice 1998).
F. Pigafetta, lettera dedicatoria a Giulio Savorgnano, cit., carte bv–b2r.
F. Pigafetta, lettera dedicatoria a Giulio Savorgnano, cit., carta bv.
Cfr. (Prinz 1983, 343-353). Alle pagine 351–353 è riportata la trascrizione dello scritto di Pigafetta, che così si chiude: “Et si lascerà intendere d’haver in grado cotali invenzioni, et in strumenti, et modelli militari in breve tempo vedrà pieno tutto il luogo di scelte cose, anzi per contenere ponti di picche, di barche, et d’odri, et di botti di varij trovati, et freschi et parapetti da resistere ad ogni impetto di bombarda, et trincee mobili sicure, et artiglierie fatte di pezzi, et anche senza metallo forti, et simili, bisognerà per aventura aggradirlo.” La nota manoscritta di Pigafetta si trova alla Biblioteca Ambrosiana (collocazione: S 97 Sup., 385-390). V. anche (Prinz 1988).
Archivio di Stato di Venezia, Secreta, Materie miste notabili, reg. 13, cc. 55v–56: “Questi 29 quesiti Giulio Savorgnano li fece domandare da un suo ragazzo nano al famoso Nicolò Tartaglia del 1542, a fine di farlo ragionare cose dilettevole.” Cfr. anche il catalogo della mostra Ambiente scientifico veneziano tra cinque e seicento, Testimonianze d’archivio (Tiepolo 1985, 35) e (Carugo 1979, in particolare nota 87, pp. LVII–LVIII).
A questo elenco provvisorio deve essere aggiunto almeno il nome di Giacomo Contarini, anche se non direttamente coinvolto nella trasportatione. Sulla sua collezione, che comprendeva anche strumenti matematico-meccanici, cfr. (Hochmann 1987). Sono noti e ben documentati i contatti tra Galileo e Contarini, entrambi in stretto rapporto con Sarpi, Pinelli e l’ambiente urbinate.
Sulle attività di Guidobaldo nel campo architettonico cfr. (Calegari 2004) e i saggi di Grazia Calegari e Francesco Menchetti in questo volume.
Guidobaldo del Monte, Meditatiunculae de rebus mathematicis, Bibliothèque Nationale de France, Ms Lat. 10246. Su questo manoscritto cfr. (Tassora 2001).
Su quest’opera cfr. (Becchi 2004; Baldi 2010). Cfr. anche (Aristotele 2000 e 1936). Sulla tormentata storia editoriale delle Exercitationes baldiane v. (Becchi 2009). Le Exercitationes, che sin dal frontespizio indicano la stretta familiarità con la parafrasi che Guidobaldo aveva dedicato ai due libri di Archimede sugli equiponderanti (cfr. Monte 1588), si incastonano alla perfezione in quel lavoro di sistematico scavo della matematica e della meccanica antica promosso dalla scuola commandiniana. L’attribuzione dei Problemi meccanici ad Aristotele era già in discussione nel Rinascimento.
Per un regesto delle numerose opere di Baldi, a stampa e manoscritte, si rimanda a (Serrai 2002).
Tra le varie testimonianze si riporta qui quella di Fabrizio Scarloncino (che riprende informazioni fornite dallo stesso Baldi), autore del De vita et scriptis Bernardini Baldi, premesso all’opera baldiana In mechanica Aristotelis problemata exercitationes (Baldi 1621, le pagine del De vita non sono numerate): “Pestilentia ex eo Gymnasio exactus in Patriam redijt, vbi quinquennium integrum Federico Commandino affixus omnes Matheseos partes perdidicit, cui viro in delineandis figuris ad Euclidis, Pappi, & Heronis monumenta manum commodauit.”
Lettera di Don Ferrante Gonzaga al Marchese Cornelio Bentivoglio, datata 1 Maggio 1602: cfr. (Campori 1855, 29). Don Ferrante fa riferimento ad una lettera di Baldi del 22 Aprile 1602: “Io scrissi al S.r Donesmondi che dicesse un non so che all’E.V. del ponte da farsi al Baccanello; se le viene occasione di scrivere al S.r Marchese, potrà tenergliene una parola” (Ronchini 1873, 133-134).
Su questo testo cfr. (Bernini 2002).
Scarloncino, De vita et scriptis Bernardini Baldi (Baldi 1621), pagine non numerate: “scio dixisse aliquando Adrianum Romanum e Polonia reuersum, vbi Vitruuium Palatino cuidam explicauerat, si commentarium Baldi in Polonia adhibere potuissem, aurum quod mecum attuli emunxissem, quia satis fecissem muneri labore nullo.”
“Raro tamen boni Architecti eo loco aptare solent, eo quod eiusmodi claues vel pulcherrimis ædificijs minuant gratiam. Vnde fit vt nunquam satis laudetur Lucianus ille Benuerardus Lauranensis Dalmata, qui nullibi apparentes eas posuit in admirabili illa Vrbini Aula, quam Federico Feltrio, felicissimo æque & inuictissimo Duci, ædificauit” (Baldi 1621, 110).
Cfr. (Narducci 1886, 464). Questo passo e, in particolare, l’espressione “ornati, come si dice, di tutte l’arme,” è un’esplicita citazione dello stesso Vitruvio (De Architettura, libro I). La trascrizione qui di seguito riportata è tratta dall’edizione (Vitruvio 1997, vol. I, 12): “Itaque architecti qui sine litteris contenderant ut manibus essent exercitati, non potuerunt effimere ut haberent pro laboribus auctoritatem, qui autem ratiocinationibus et litteris solis confisi fuerunt, umbram non rem persecuti videntur. At qui utrumque perdidicerunt, uti omnibus armis ornati citius cum auctoritate quod fuit propositum sunt adsecuti.” In un’altra versione della Vita di Vitruvio (M. Vitruvii Pollionis Architecti Vita), posta in appendice al suo De verborum Vitruvianorum significatione (Baldi 1612, p. 199), Baldi scrive: “Hinc fit, ut Vitruvium ab ijs architectis seiungamus, qui ab optimis artibus & scientijs imparati, nobilissimis architecturae studijs, illotis ut aiunt manibus pedibusque, tanquam profani, temere ultro se ingerunt. Ipse enim omnibus armis ornatus, militiae huic nomen dedit, quare sit, ut ei, licet architecto, locum non immerito inter Mathematicos & Geometras ipsos decernamus.” Sulle Vite de’ matematici vedi anche (Baldi 1998).
“Cur eiusdem magnitudinis lignum facilius genu frangatur si quispiam aeque diductis manibus extrema comprehendens fregerit, quam si iuxta genu. Et si terrae applicans pede superposito manu hinc inde diducta confregerit quam prope” (Baldi 1621, 91).
“Quare, quo longiora sunt ligna, tanto imbecilliora fiant, & si tolluntur, inflectuntur magis: tametsi quod breue est ceu bicubitum fuerit, tenue, quod vero cubitorum centum crassum?” (Baldi 1621, 95).
Nessun commentatore aveva mai dedicato più di due pagine all’argomento, l’estensione della trattazione rivela un interesse specifico per il tema. Per la lunga serie di commenti e traduzioni rinascimentali ai Problemi meccanici cfr. (Rose and Drake 1971). Vedi anche (Lohr 1974; 1975; 1976; 1977; 1978; 1979; 1980; 1982).
“Modo vt ex hac contemplatione, quæ alias inutilis videtur, aliquam vtilitatem capiamus, & ex his quæ contemplabimur, Architecti prudentiores fiant, ist hæc ipsa, de quibus agimus, ad rem ædificatoriam commode aptabimus” (Baldi 1621, 98).
Cfr. (Alberti 1485, Libro III). Per la traduzione e la trascrizione qui riportate cfr. (Alberti 1966, 234-235): “Et enim ducendi arcus rationem traxisse homines hinc puto: nam, cum viderent
trabes duas iunctis capitibus posse imis pedibus divaricatis ita firmari, ut
mutuo innexu paribusque contra se ponderibus sisterent, placuit inventum, et
coeperunt istoc opere displuvia ædificiis tecta apponere. Post id,
fortasse cum ex instituto maiorem cooperire aream trabium brevitate
nequivissent, intermedium ad sublimia truncorum capita aliquid interposuere,
ut essent prope atque apud Græcos littera
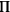 , appositumque ipsum id
fortassis cuneum appellavere. Succedente inde argumento multiplicatis cuneis
istiusmodi arcus effigiem effectam spectantes probavere, eamque ducendi arcus
rationem ad opera lapidea transferentes integrum additamentis arcum
effecere.”
, appositumque ipsum id
fortassis cuneum appellavere. Succedente inde argumento multiplicatis cuneis
istiusmodi arcus effigiem effectam spectantes probavere, eamque ducendi arcus
rationem ad opera lapidea transferentes integrum additamentis arcum
effecere.”
Ovviamente l’indagine dovrebbe estendersi a tutta la cerchia pesarese-urbinate, coinvolgendo Muzio Oddi e la famiglia Barocci. Di Simone Barocci Baldi scrive: “il quale con tanta industria lavora compassi, ed istrumenti matematici, che non avendo chi lo pareggi, si può dire senz’arroganza, che la sua bottega sia la bottega del mondo; il che non mi vergogno io di affermare, ne temo di esserne tenuto bugiardo, essendo ciò notissimo a tutti quelli, che attendono a’detti esercizj, e nell’Italia, e fuori” (Baldi 1724, 33-34). Galileo fu uno tra i tanti a riconoscere l’eccellenza di questa “bottega del mondo” che aveva sede ad Urbino.
A questo riguardo sarebbe interessante analizzare nel dettaglio le relazioni tra il cardinale Cinzio Aldobrandini e il cardinale Francesco Maria del Monte, fratello di Guidobaldo del Monte, da mettere in rapporto con Clemente VIII (ossia Ippolito Aldobrandini, zio dei cardinali Cinzio e Pietro Aldobrandini), pontefice nel periodo 1592–1605. Su Francesco Maria una buona base di partenza è l’opera di Zygmunt Waźbiński, recentemente scomparso (Waźbiński 1994).
Il manoscritto fa parte del Fondo Albani, ms XIII.F.25. Le carte sono state messe in relazione con le Exercitationes da chi scrive, ma i volumi baldiani conservati nella Biblioteca Nazionale di Napoli sono noti da tempo. Luigi Ruberto ha descritto il contenuto del manoscritto XIII.F.25 nell’opera (Ruberto 1882, 84-86) e Serrai ha pubblicato una trascrizione completa del componimento Il Genio, ouero la Misteriosa Peregrinatione (“comminciata a scrivere Adi 29 d’Ottobre del M.DLXXXIII,” scrive l’autore accanto al titolo), che occupa le prime pagine dello stesso codice (Serrai 2002, 174-184). Del Genio Guido Zaccagnini (1908) aveva trascritto e pubblicato alcuni brani nel suo Bernardino Baldi nella vita e nelle opere. Zaccagnini si era già occupato di Baldi nel volume (Zaccagnini 1902; l’esemplare consultato da chi scrive, conservato presso la Staatsbibliothek di Berlino, presenta un doppio frontespizio, il primo è datato 1903). Evidentemente i testi letterari hanno distratto l’attenzione degli studiosi e reso insignificanti i frammenti citati. Una conferma si trova nella nota redatta da Paul Lawrence Rose intitolata Rediscovered manuscripts of the “Vite de’matematici” and mathematical works by Bernardino Baldi (1553–1617), dove a proposito dei manoscritti di Napoli si legge: “As Professor Rienstra kindly informs me, none of the Baldi items at Naples is of mathematical interest.” La nota di Rose è pubblicata in (Rose 1974), il passo citato si trova a p. 274, nota 9. Di Rose cfr. anche (Rose 1975).
T. Gallaccini, Perigonia, o vero degli angoli, Biblioteca degli Intronati di Siena, Ms. L. IV. 5. Testo a disposizione in formato digitale nel sito http://echo.mpiwg-berlin.mpg.de/content. Vedi anche (Gallaccini 2003).
Cfr. (Prado and Villalpando 1596-1605).
Cfr. (Giusti 1990, XII, Nota 1). Anche l’edizione curata da Adriano Carugo e Ludovico Geymonat (Galilei 1958) non approfondisce gli aspetti qui considerati. Il tema degli atomi e degli indivisibili è invece stato affrontato nel dettaglio da Paolo Galluzzi in un saggio recente (Galluzzi 2011). Cfr. anche (Valleriani 2010).
