Wir haben immer noch nicht festgelegt, was wir unter „Algebra“
verstehen wollen.
VAT 8512
Vs.
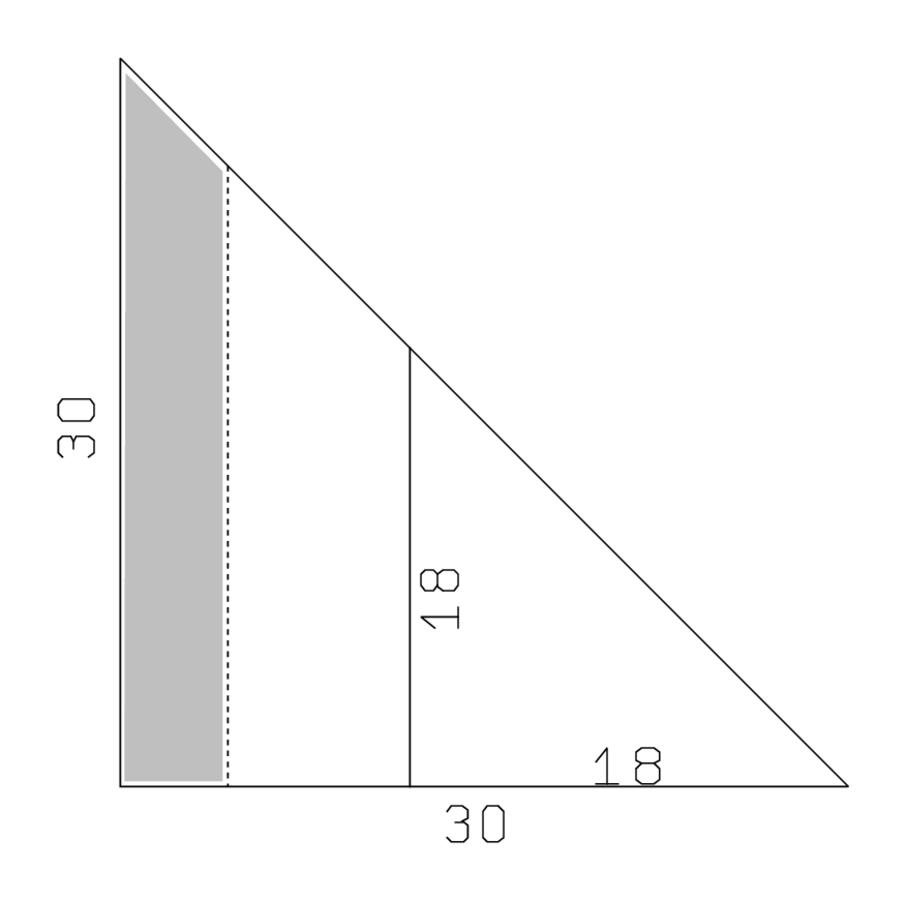
(1)Ein Dreieck. 30 die Breite. Im Innern zwei Felder,
(2)die obere Fläche über die untere Fläche, 7‵ ging sie hinaus.
(3)Die untere Absteigende über die obere Absteigende, 20 ging sie hinaus.
(4)Die Herabsteigende und die Querlinie, was?
(5)Und die Flächen der beiden Felder, was?
(6)Du, 30 die Breite setze, 7‵ was die obere Fläche über die untere Fläche hinausging, setze,
(7)und 20 was die untere Herabsteigende über die obere Herabsteigende hinausging, setze.
(8)igi 20 was die untere Herabsteigende über die obere Herabsteigende hinausging
(9)spalte ab: 3′ auf 7‵ was die obere Fläche über die untere Fläche hinausging,
(10)erhöhe, 21 möge Dein Kopf halten!
(11)21 zu 30 der Breite füge hinzu: 51
(12)zusammen mit 51 lasse enthalten: 43‵21
(13)21 was Dein Kopf behalten hat zusammen mit 21
(14)lasse enthalten: 7‵21 zu 43‵21 füge hinzu: 50‵42.
(15)50‵42 brich entzwei: 25‵21.
(16)Das Gleiche von 25‵21 was? 39.
(17)Aus 39, 21 das Gehaltene, reiße heraus, 18.
(18)18 welche Dir übrig bleiben ist die Querlinie.
(19)Gut, wenn 18 die Querlinie ist,
(20)die Herabsteigenden und die Flächen der beiden Felder sind was?
(21)Du, 21 welches zusammen mit sich selbst Du enthalten lassen hast, aus 51
(22)reiße heraus: 30 bleiben Dir. 30 welche Dir bleiben
(23)brich entzwei, 15 auf 30 welche Dir bleiben, erhöhe
(24)7‵30 möge Dein Kopf behalten!
Kante
(1)18 die Querlinie zusammen mit 18 lass enthalten:
(2)5‵24 aus 7‵30 welche Dein Kopf hält
(3)reiße heraus: 2‵6 bleiben Dir.
Rs.
(1)Was zu 2‵6 soll ich setzen
(2)was mir 7‵, welches die obere Fläche über die untere Fläche hinausging, gibt?
(3)3°20′ setze. 3°20′ auf 2‵6 erhöhe, 7‵ gibt es Dir.
(4)30 die Breite über 18 die Querlinie, wie viel geht es darüber hinaus? 12 geht es darüber hinaus.
(5)12 auf 3°20′, was Du gesetzt hast, erhöhe, 40.
(6)40 die obere Herabsteigende.
(7)Gut, wenn 40 die obere Herabsteigende ist,
(8)die obere Fläche ist was? Du, 30 die Breite,
(9)18 die Querlinie häufe an: 48 brich entzwei: 24.
(10)24 auf 40 die obere Herabsteigende erhöhe, 16‵.
(11)16‵ die obere Fläche. Gut, wenn 16‵ die obere Fläche,
(12)die untere Herabsteigende und die untere Fläche was?
(13)Du, 40 die obere Herabsteigende zu 20 welches die obere Herabsteigende über die untere Herabsteigende hinausgeht,
(14)füge hinzu, 1‵ die untere Herabsteigende.
(15)18 die Querlinie brich entzwei: 9
(16)auf 1‵ die untere Herabsteigende erhöhe, 9‵.
(17)9‵ die untere Fläche.
Viele altbabylonischen mathematischen Probleme behandeln die Aufteilung von Feldern. Die mathematische Substanz kann variieren – manchmal ist die Form des Feldes irrelevant und
nur die Fläche wird zusammen mit den spezifischen Bedingungen für seine Teilung angegeben; manchmal, so wie hier, wird nach einer Aufteilung einer bestimmten geometrischen Form
gefragt.
Bereits vor 2200 v.Chr. wussten mesopotamische Feldmesser, wie man ein Trapez durch eine parallele Transversale in zwei gleich große Teile teilt; wir werden gleich darauf zu sprechen kommen, wie sie das gemacht haben. Eine ähnliche Halbierung eines Dreiecks lässt sich ohne die Benutzung irrationaler Größen nicht exakt ausführen – und dies bedeutet, dass die altbabylonischen Feldmesser dies nur näherungsweise machen konnten, was allerdings nicht zu den üblichen Lernzielen gehört hat.
Das vorliegende Problem dreht sich um eine Variante der Aufteilung eines Dreiecks, die man exakt ausführen kann. Wie wir in Zeilen 1–3 sehen können und wie in Abbildung 5.1 gezeigt wird, wird ein dreieckiges Feld von einer „Querlinie“, also einer parallelen Transversale, in zwei Stücke geteilt (eine „obere Fläche“ und eine „untere Fläche“). Der Einfachheit halber nehmen wir an, dass das Dreieck rechtwinklig ist. Es ist ziemlich sicher, dass der Autor des Texts dies auch getan hat, und dass die „Herabsteigenden“ daher Teile der Seite sind; wenn wir allerdings die „Herabsteigenden“ als Höhen interpretieren, gelten die Rechnungen auch für ein schiefwinkliges Dreieck.
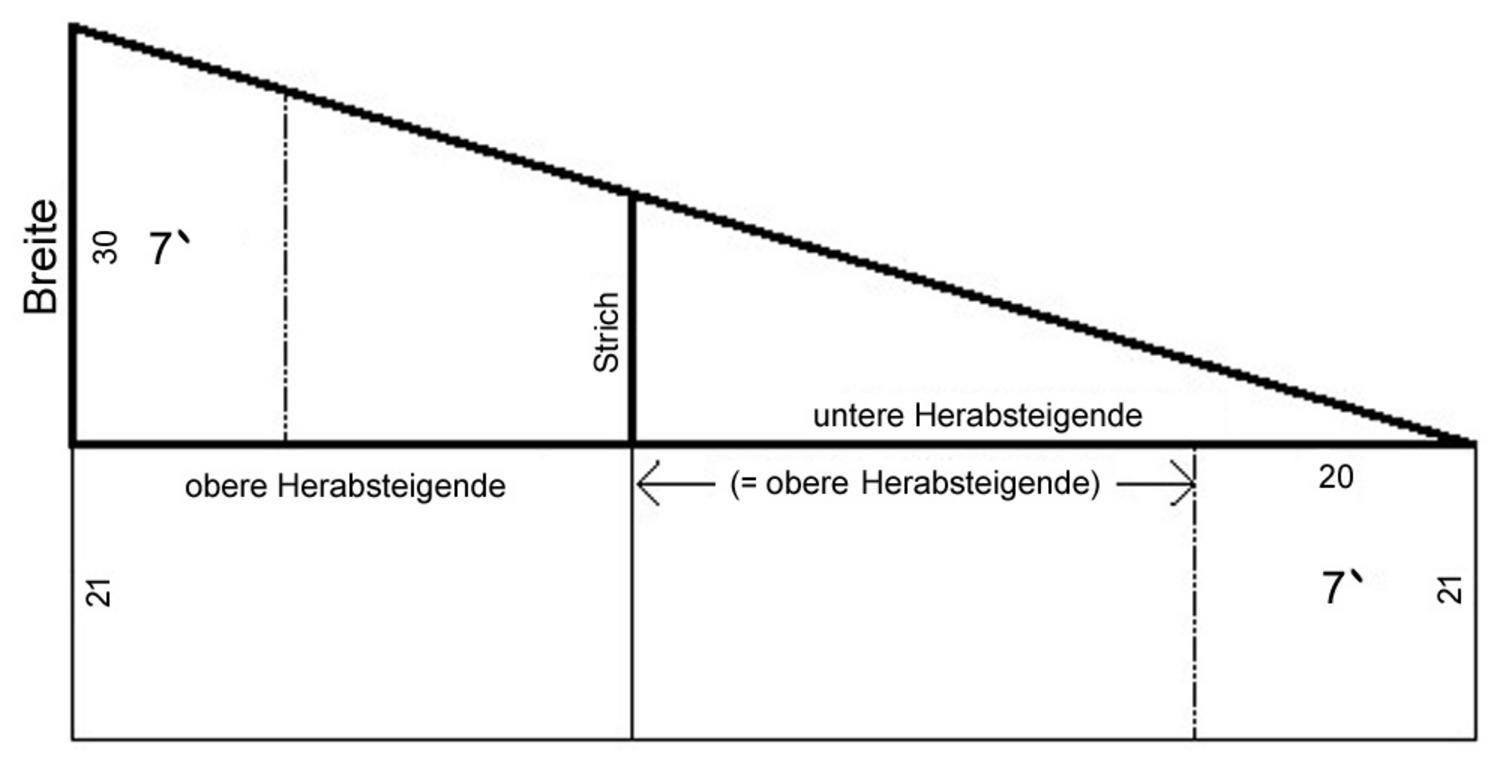
Abb. 5.1: Das dreieckige geteilte Feld von VAT 8512, mit dem Hilfsrechteck.
Die beiden Stücke haben also verschiedene Flächen. Wir kennen allerdings die Differenz der beiden Flächen, sowie die Differenz der beiden dazugehörigen Herabsteigenden. Die Lösung benutzt einen unerwarteten und eleganten Trick und mag daher schwer zu verstehen sein.
Zeilen Vs. 8–10 „erhöhen“ das igi der Differenz der beiden
„Herabsteigenden“ auf die Differenz der beiden „Flächen“.
Dies bedeutet, dass der Text die Breite eines Rechtecks findet, dessen Länge
der Differenz der beiden Teilhöhen und dessen Fläche gleich der Differenz der beiden
Teilflächen ist. Dies Breite (die 21 ist) wird zuerst im Kopf behalten und dann zur
Breite des Dreiecks hinzugefügt.
Das Ergebnis ist ein Dreieck mit einem angehängten Rechteck – zusammengenommen
das Trapez in Abbildung 5.1. Verlängert man die Querlinie zu einer parallelen
Transversale des Trapezes, dann finden wir, dass das Trapez in zwei gleich große Teile
aufgeteilt wird – und dies ist das Problem, das bereits die altbabylonischen Feldmesser
Die Zeilen Vs. 11–16 zeigen, wie sie es gemacht haben: Das Quadrat auf der halbierenden Transversale ist festgelegt als der Mittelwert zwischen den Quadraten der parallelen Seiten. Die dabei verwendeten Operationen („enthalten lassen“ und „abbrechen“) zeigen, dass dieser Prozess wirklich mit Hilfe geometrischer Quadrate und Mittelwerten gedacht ist. Abbildung (5.2) zeigt, warum das Verfahren ein korrektes Ergebnis liefert.
Per definitionem hat der Mittelwert gleichen Abstand zu den beiden Extremen.
Also muss das Gnomon zwischen 21 und 39 gleich demjenigen zwischen
39 und 51 sein:
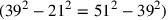 ; die Hälfte dieser
Gnomone – die beiden Teile des schattierten Trapezes – müssen daher ebenfalls
gleich sein. Zuerst gilt dies nur für ein Trapez, das entlang der Diagonalen
aus einem Quadrat ausgeschnitten ist, aber wir können uns vorstellen, dass das
Quadrat zu einem Rechteck gezogen wird und vielleicht zu einem Parallelogramm
verdreht wird – keine dieser Operationen ändert das Verhältnis der Flächen
oder paralleler Strecken, und dies erlaubt die Erzeugung eines beliebigen
Trapezes. Dieses Trapez wird immer noch halbiert
; die Hälfte dieser
Gnomone – die beiden Teile des schattierten Trapezes – müssen daher ebenfalls
gleich sein. Zuerst gilt dies nur für ein Trapez, das entlang der Diagonalen
aus einem Quadrat ausgeschnitten ist, aber wir können uns vorstellen, dass das
Quadrat zu einem Rechteck gezogen wird und vielleicht zu einem Parallelogramm
verdreht wird – keine dieser Operationen ändert das Verhältnis der Flächen
oder paralleler Strecken, und dies erlaubt die Erzeugung eines beliebigen
Trapezes. Dieses Trapez wird immer noch halbiert
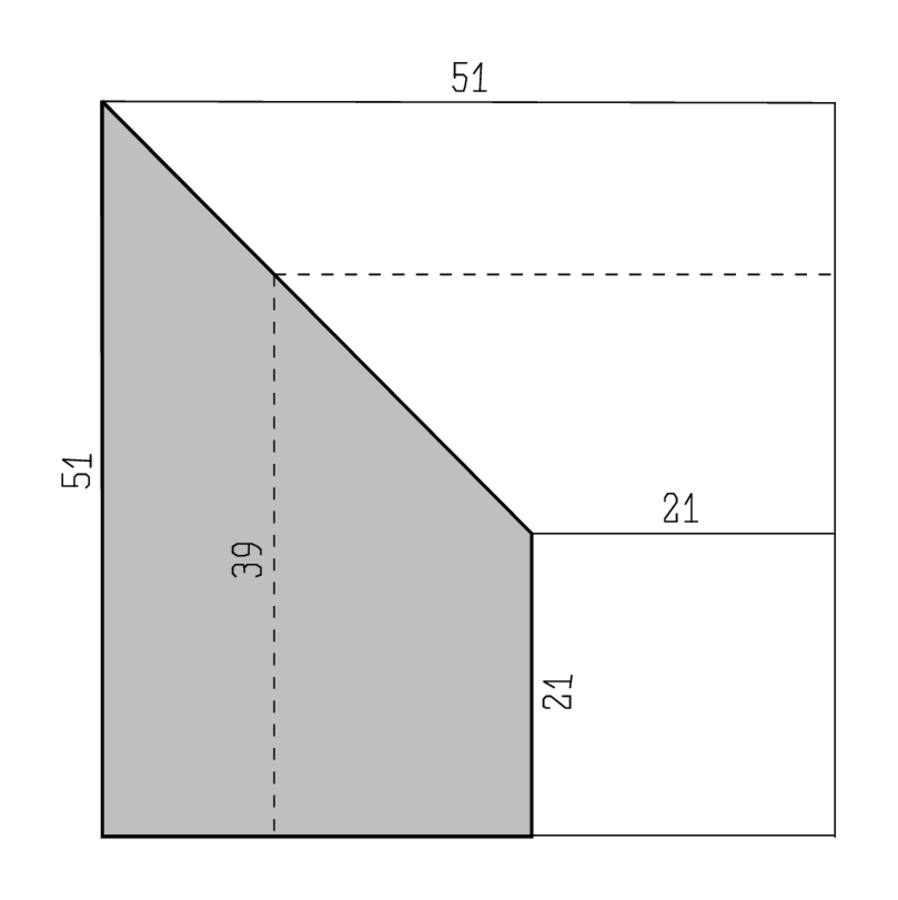
Abb. 5.2: Die Halbierung des Trapezes von BM 8512.
Wir bemerken, dass die Operation des „Langziehens“ auf einen
Wechsel des Maßstabs
Möglicherweise wurde die Regel zuerst auf der Basis konzentrischer
Quadrate
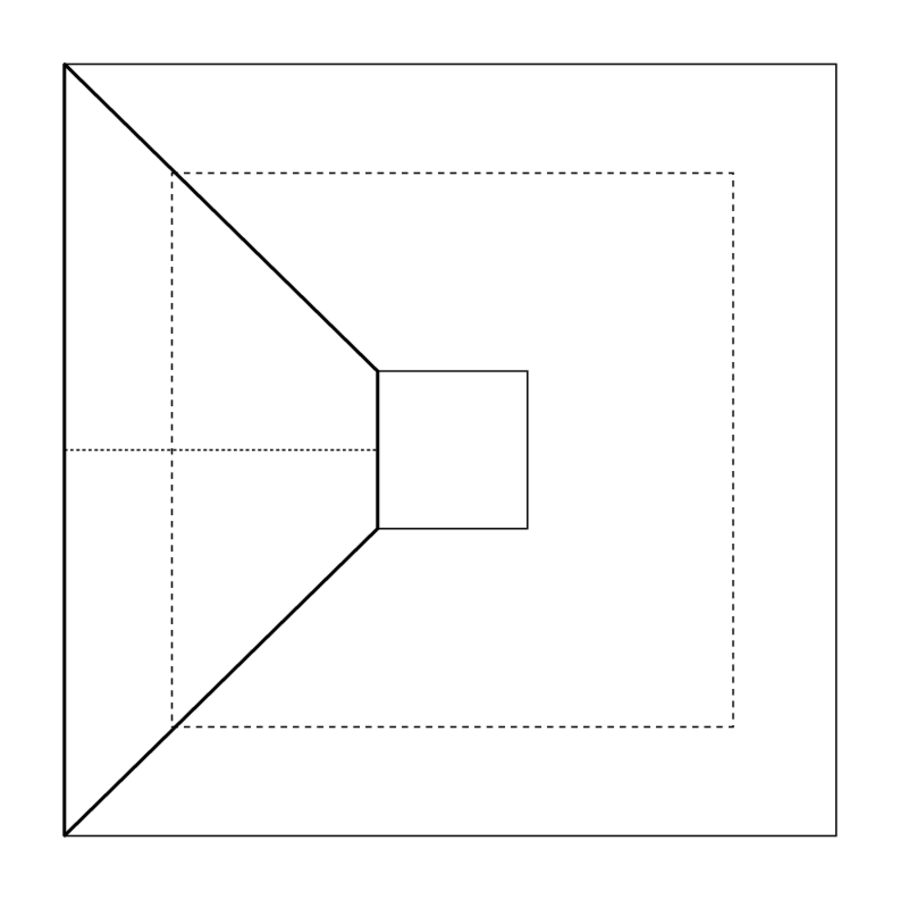
Abb. 5.3: Die Halbierung des Trapezes erklärt durch konzentrische Quadrate.
Zeile Vs. 17 findet also die halbierende Transversale; sie ergibt sich
als 39, und die „Querlinie“ zwischen den beiden ursprünglichen
Stücken muss daher die Länge
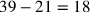 haben.
haben.
Die nächsten Schritte erscheinen merkwürdig. Zeilen Vs. 21–22 scheinen die Breite des Dreiecks zu berechnen, aber die war eine der gegebenen Größen der Aufgabe. Zweifellos bedeutet dies, dass wir Abbildung 5.1 hinter uns gelassen haben und das Argument jetzt auf einer Figur wie in Abbildung 5.2 beruht. Wenn wir die zusätzliche Breite 21 eliminieren, dann bleibt ein Dreieck übrig, das dem ursprünglichen Dreieck entspricht, aber gleichschenklig ist – siehe Abbildung 5.4.
Um die „obere Herabsteigende“ zu finden, benutzt der Text einen
falschen Ansatz
Die Zeilen Vs. 23–24 berechnen, dass die Fläche des falschen Dreiecks
7‵30 ist. Die beiden weißen Flächen sind gleich, und ihre
summe muss
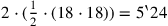 sein.
Die schattierte Fläche – welche der Differenz der Flächen der beiden
Teilstücke entspricht – muss daher
sein.
Die schattierte Fläche – welche der Differenz der Flächen der beiden
Teilstücke entspricht – muss daher
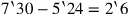 (Kante 1–3) sein.
(Kante 1–3) sein.
Wir wissen aber, dass die Differenz 7‵ ist und nicht 2‵6.
Die Zeilen Rs. 1–3 ergeben, dass die Differenz 2‵6, die aus dem
falschen Ansatz resultiert, mit 3°20′ multipliziert werden
muss, um die wahre Differenz 7‵ zu erhalten. Da die Breite bereits
den gewünschten Wert hat, müssen wir die Länge und die
„Herabsteigenden“ mit diesem Faktor multiplizieren. Die
„obere Herabsteigende“ wird also
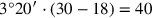 sein (Zeile Rs. 6). Danach ist alles sehr einfach; es könnte sogar noch
einfacher sein, aber der gewählte Weg stimmt besser mit dem pädagogischen
Stil überein, den wir von TMS XVI #1
sein (Zeile Rs. 6). Danach ist alles sehr einfach; es könnte sogar noch
einfacher sein, aber der gewählte Weg stimmt besser mit dem pädagogischen
Stil überein, den wir von TMS XVI #1
Die Art und Weise, wie dieses Problem gelöst wurde, unterscheidet sich sicherlich von dem, was wir bisher angetroffen haben. Jedoch gibt es auch Gemeinsamkeiten, die aus der Vogelperspektive deutlicher zu sehen sind.
Der Maßstabswechsel
Der „analytische“ Charakter
Eine Lösung durch eine Gleichung ist immer analytisch. Um dies zu verstehen,
betrachten wir noch einmal unsere moderne Lösung von TMS XIII . Wir machen dasselbe mit der
Verkaufsrate (die wir
. Wir machen dasselbe mit der
Verkaufsrate (die wir
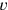 nennen). Die Gesamtinvestition ist daher
nennen). Die Gesamtinvestition ist daher
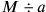 , der Gesamtverkaufspreis
, der Gesamtverkaufspreis
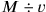 , und der Gewinn
folglich
, und der Gewinn
folglich
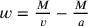 . Dann multiplizieren wir
mit
. Dann multiplizieren wir
mit
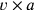 und so weiter.
und so weiter.
Wir behandeln also
 und
und
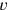 , als ob sie bekannte Zahlen
wären; wir tun so, als hätten wir eine Lösung und wir beschreiben ihre Merkmale.
Danach leiten wir Folgerungen ab und finden zum Schluss, dass
, als ob sie bekannte Zahlen
wären; wir tun so, als hätten wir eine Lösung und wir beschreiben ihre Merkmale.
Danach leiten wir Folgerungen ab und finden zum Schluss, dass
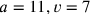 ist.
ist.
Sogar die Lösungen mit der altbabylonischen
cut-and-paste-Methode
Die Lösung des vorliegenden Problems ist ebenfalls analytisch. Wir
nehmen an, dass das Dreieck durch ein Rechteck derart
ergänzt wird, dass der verlängerte „Querlinie“ das sich ergebende
Trapez in gleich große Teile teilt, und dann berechnen wir, wie groß
die Breite des Rechtecks sein muss, wenn dies der Fall ist; und so weiter.
Obwohl es seine Berechtigung hat, erscheint die Unterscheidung zwischen
„algebraischen“ Problemen (solche, die man leicht in moderne
Gleichungen übersetzen kann) und „quasi-algebraischen“
Problemen
BM 85200 + VAT 6599 #6
Vs. I
(9)Eine Ausgrabung. So viel wie die Länge ist die Tiefe. 1 die Erde habe ich ausgerissen. Den Grund und die Erde habe ich angehäuft, 1°10′. Länge und Breite, 50′. Länge, Breite, was?
(10)Du, 50′ auf 1, die Umrechnung, erhöhe, 50′ siehst Du. 50′ auf 12 erhöhe, 10 siehst Du.
(11)Stelle 50′ sich gegenüber, 41′40″ siehst Du; auf 10 erhöhe, 6°56′40″ siehst Du. Sein igi spalte ab, 8′38″24‴ siehst Du;
(12)auf 1°10′ erhöhe, 10′4″48‴ siehst Du, 36′, 24′, 42′ sind Gleiche.
(13)36′ auf 50′ erhöhe, 30′ die Länge. 24′ auf 50′ erhöhe, 20′, die Breite; 36′ auf 10 erhöhe, 6, die Tiefe.
(14)Das Verfahren.
Dies ist ein Problem dritten Grades,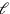 [nindan],
Breite
[nindan],
Breite
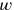 [nindan] und Tiefe
[nindan] und Tiefe
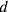 [kùš].
Die Länge ist gleich der Tiefe, aber wegen der verschiedenen Maßeinheiten in
diesen beiden Richtungen bedeutet dies
[kùš].
Die Länge ist gleich der Tiefe, aber wegen der verschiedenen Maßeinheiten in
diesen beiden Richtungen bedeutet dies
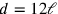 .
.
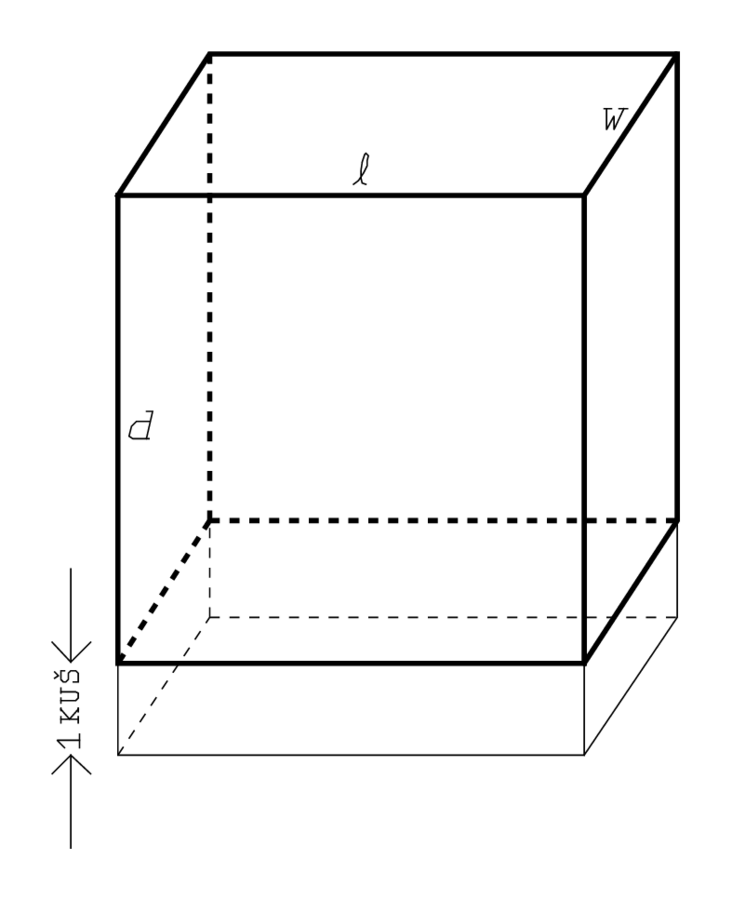
Abb. 5.5: Die Ausgrabung 1 kùš nach unten erweitert.
Weiter ist die Summe von Länge und Breite
![[ℓ+w=]](../../../media/textbooks/3/7/EOAineq_7_19.png) 50′,
und die Summe des Volumens der Erde, der „herausgerissen“
(also ausgegraben)2
wurde und des „Grunds“ (der Grundfläche) ist
50′,
und die Summe des Volumens der Erde, der „herausgerissen“
(also ausgegraben)2
wurde und des „Grunds“ (der Grundfläche) ist
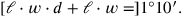
|
Diese letzte Gleichung kann in
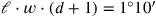
|
umgeformt werden – wenn also die Ausgrabung 1 kùš tiefer ausgeführt
worden wäre, dann wäre das Volumen gleich
1°10′ [nindan2
 kùš]
gewesen (siehe Abbildung 5.5).3
kùš]
gewesen (siehe Abbildung 5.5).3
Die Lösung basiert auf einer feinsinnigen Variante des falschen
Ansatzes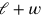 .
In horizontalen Maßen ist die Kantenlänge
.
In horizontalen Maßen ist die Kantenlänge
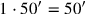 [nindan], denn der
„Umrechnungsfaktor“ von nindan in nindan
besteht in einer Multiplikation mit 1. In vertikalen Maßen ist es
[nindan], denn der
„Umrechnungsfaktor“ von nindan in nindan
besteht in einer Multiplikation mit 1. In vertikalen Maßen ist es
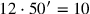 kùš, weil der
„Umrechnungsfaktor“ von nindan in kùš
in einer Multiplikation mit 12 besteht (beide Umrechnungen finden
in Zeile 10 statt).
kùš, weil der
„Umrechnungsfaktor“ von nindan in kùš
in einer Multiplikation mit 12 besteht (beide Umrechnungen finden
in Zeile 10 statt).
Zeilen 11-12 finden das Volumen des Bezugswürfels als 6°56′40″. Dieses Volumen ist 10′4″48‴ mal in der erweiterten Ausgrabung enthalten.
Wir wollen uns nun vorstellen, dass die Kanten der erweiterten Ausgrabung
durch die Kanten des Bezugswürfels gemessen werden. Wenn p
angibt, wie oft die Länge
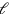 von 50′ nindan
gemessen wird, und q, wie oft die Tiefe
von 50′ nindan
gemessen wird, und q, wie oft die Tiefe
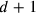 kùš
von 10 kùš (= 50´ nindan) gemessen wird, dann ist
kùš
von 10 kùš (= 50´ nindan) gemessen wird, dann ist
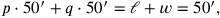
|
und daher
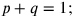
|
weiter ist
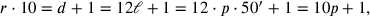
|
daher
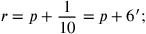
|
und schließlich
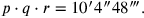
|
Wir müssen also 10′4″48‴ als das Produkt dreier Faktoren
p, q und r ausdrücken, welche diesen
Bedingungen genügen. Dies macht der Text in Zeile 12, wo die Faktoren
als „die Gleichen“
36′, 24′ und 42′ erscheinen.
Danach findet Zeile 13
 ,
,
 und
und
 .
.
Die Faktorisierung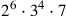 )
als das Produkt von drei Zahlen P, Q und R
ausdrücken, wo
)
als das Produkt von drei Zahlen P, Q und R
ausdrücken, wo
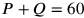 und
und
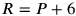 gilt4
Wenn wir den allgemeinen Charakter der altbabylonischen Mathematik
berücksichtigen, dann können wir sogar behaupten, dass der Text
die Antwort zwangsläufig nur deshalb aus dem Ärmel schütteln darf,
weil es zwar möglich (aber recht aufwendig) wäre, sie ohne Magie
zu finden. Wir wollen zuerst annehmen, dass
gilt4
Wenn wir den allgemeinen Charakter der altbabylonischen Mathematik
berücksichtigen, dann können wir sogar behaupten, dass der Text
die Antwort zwangsläufig nur deshalb aus dem Ärmel schütteln darf,
weil es zwar möglich (aber recht aufwendig) wäre, sie ohne Magie
zu finden. Wir wollen zuerst annehmen, dass
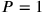 ist.
Wegen
ist.
Wegen
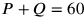 wird
wird
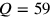 sein, was
unmöglich ist. Die Annahmen
sein, was
unmöglich ist. Die Annahmen
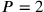 und
und
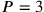 können analog ausgeschlossen werden.
können analog ausgeschlossen werden.
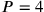 gibt
gibt
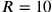 , was ebenfalls ausgeschlossen ist –
10‶4‵48 enthält keinen Faktor 5.
, was ebenfalls ausgeschlossen ist –
10‶4‵48 enthält keinen Faktor 5.
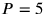 ist unmöglich;
ist unmöglich;
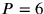 gibt
gibt
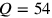 und
und
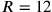 ,
was nicht sein kann, sowohl weil der Faktor 7 fehlt und weil eine
Probe zeigt, dass das Produkt nicht den Bedingungen genügt.
Der nächste Wert von P, der nicht zu unmöglichen Werten für
,
was nicht sein kann, sowohl weil der Faktor 7 fehlt und weil eine
Probe zeigt, dass das Produkt nicht den Bedingungen genügt.
Der nächste Wert von P, der nicht zu unmöglichen Werten für
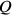 oder R führt, ist 12, was aber aus denselben
Gründen nicht sein kann.
oder R führt, ist 12, was aber aus denselben
Gründen nicht sein kann.
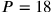 ist unmöglich, weil das Produkt nur etwa
halb so groß ist wie nötig.
ist unmöglich, weil das Produkt nur etwa
halb so groß ist wie nötig.
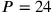 und
und
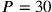 funktionieren aus
denselben Gründen wie bei
funktionieren aus
denselben Gründen wie bei
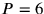 nicht. Endlich kommen wir bei
nicht. Endlich kommen wir bei
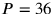 , einem Wert der passt. Hätten wir Primfaktoren gezählt, wäre es
noch leichter gewesen,
, einem Wert der passt. Hätten wir Primfaktoren gezählt, wäre es
noch leichter gewesen,
Es muss aber betont werden, dass diese Methode nur funktioniert, weil
eine einfache Lösung existiert. Dadurch unterscheidet sich dieses
Problem wesentlich von denen zweiten Grades, wo eine gute Näherung
dessen, was „gleich ist“, eine fast richtige Lösung
geben würde (und die Babylonier wussten sehr gut, wie man solche
Quadratwurzeln
Unser Text spricht von drei
„Gleichen“
Andere Aufgaben von derselben Tafel sprechen von einem einzigen
„Gleichen“; dies ist der Fall, wenn das Volumen der Ausgrabung,
gemessen durch das Bezugsparallelepiped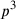 oder als
oder als
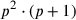 faktorisiert werden muss. Für diese beiden Funktionen existieren in der
Tat Tafeln
faktorisiert werden muss. Für diese beiden Funktionen existieren in der
Tat Tafeln exakt als „das Gleiche“.
exakt als „das Gleiche“.
Wie in der Algebra der Aufgaben zweiten Grades ist die Behandlung der
Probleme dritten Grades
Davon abgesehen gibt es nur ziemlich schwache Verbindungen zwischen Problemen zweiten und dritten Grades: die Terminologie für Operationen, die Benutzung von Tafeln, und die fundamentalen arithmetischen Operationen.
Andere Aufgaben auf derselben Tafel (alle drehen sich um quaderförmige
„Ausgrabungen“) werden auf Probleme zweiten oder gar ersten
Grades zurückgeführt. Dieser werden dann mit Techniken gelöst, die wir
schon kennen, und nicht durch Faktorisierungen.
BM 15285 #24
(1)1 uš die Gegenseite
(2)Im Innern 16 Gegenseiten
(3)habe ich niedergelegt. Ihre Flächen, was?
Dieses kleine Problem stammt von einer Tafel, welches um die 40
Aufgaben
Der obige Text erklärt den Lösungsweg nicht – dies ist bei keinem einzigen der
Aufgaben auf dieser Tafel
In Zeile 3 ist zu sehen, dass das Verb, das mit
„niederlegen“
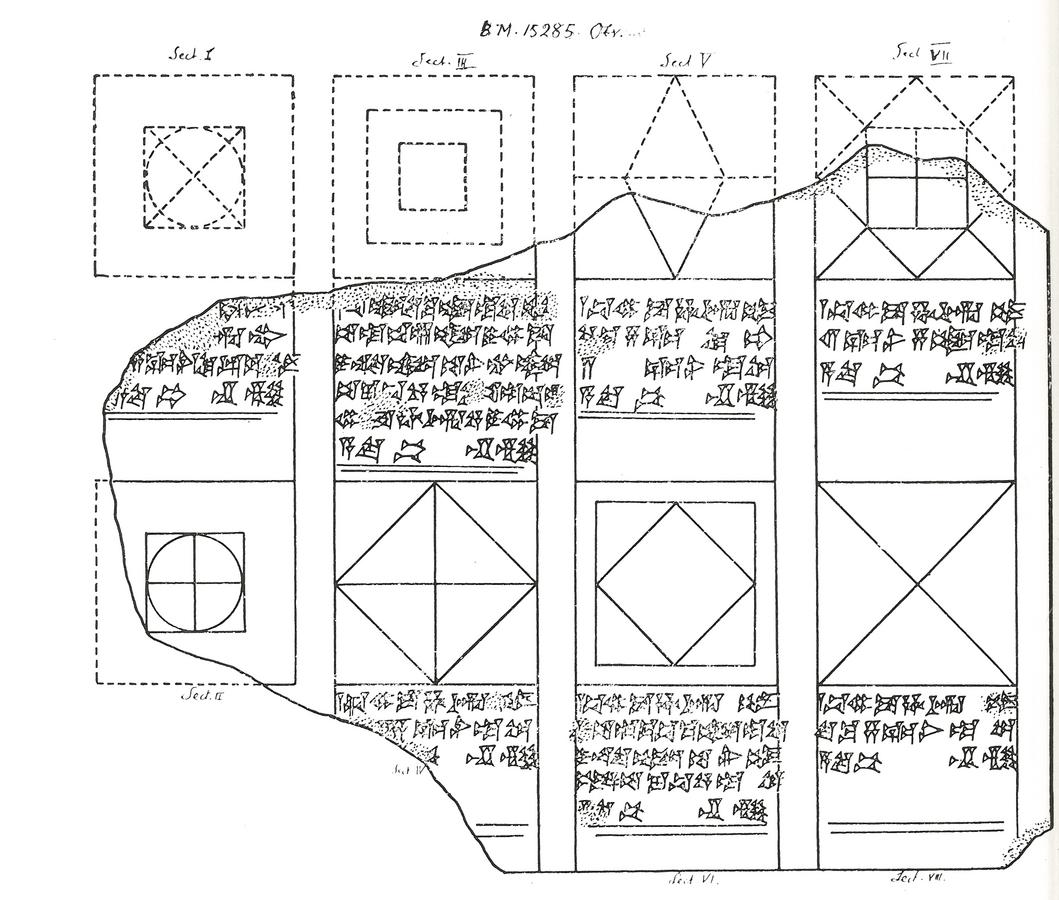
Abb. 5.6: Die Vorderseite des Hauptfragments der Tafel BM 15285. Nach C. J. Gadd, „Forms and Colours“. Revue d’Assyriologie 19 (1922), 149–159, hier S. 156.
Fußnoten
Die Antithesis der „analytischen“ Methode ist die „Synthese, in welcher die Lösung direkt konstruiert wird, gefolgt von einem Beweis, dass die Konstruktion gültig ist“. Dies ist die Beweistechnik in den Elementen Euklids, und seit der Antike gibt es ständige Beschwerden darüber, dass es dies schwieriger als unbedingt nötig macht, dieses Werk zu verstehen: der Student sieht gut, dass jeder Schritt des Beweises korrekt ist und muss folglich akzeptieren, dass das Endresultat unwiderlegbar ist – aber er versteht nicht die Gründe, warum der Autor diesen einen Schritt macht. Dadurch erscheint der Autor eher scharfsinnig als wirklich pädagogisch. Seit der Antike hat man Euklid (oder seine Vorgänger) verdächtigt, ihre Konstruktionen und Beweise erst mittels einer Analyse gefunden und die Lösung dann konstruiert zu haben, während sie ihre Spuren versteckt haben.
Der Text benutzt dasselbe Verb „herausreißen“ wie für die subtraktive Operation.
Die Aussage bezieht sich auch auf „1 die Erde, die ich herausgerissen habe“, aber diese Information wird nicht benutzt. Dies ist ein weiteres Beispiel einer Größe, die bekannt aber nicht gegeben ist. Die Kenntnis des numerischen Werts erlaubt dem Lehrer, eine Unterscheidung zwischen der wirklichen Ausgrabung („1, die Erde“) und dem Volumen der Ausgrabung zu machen, die um 1 kùš nach unten fortgesetzt wird („1°10′, die Erde“).
Um ganze Zahlen zu haben führen wir hier P = 60p = 1‵p, Q = 1‵q, und R = 1‵r ein. Dann ist PQR = 1‷pqr = 10‶4‵48.