Nach diesen Beispielen von Methoden zum Lösen von Problemen ersten Grades kommen wir nun zum eigentlichen Kern der altbabylonischen Algebra, wobei wir einmal mehr die Frage übergehen, was genau wir unter „Algebra“ im Zusammenhang mit babylonischer Mathematik verstehen wollen.
In diesem Kapitel werden wir einige einfache Probleme untersuchen, und
dies wird uns erlauben, die fundamentalen
Techniken
BM 13901 #1
Vs. I
(1)Die Fläche und meine Gegenseite habe ich angehäuft: 45′ ist es. 1, die Projektion
(2)setzt Du. Das Halbe von 1 brich ab, 30′ und 30′ lässt Du enthalten.
(3)15′ zu 45′ fügst Du hinzu: bei 1 ist 1 gleich. 30′, welche Du enthalten lassen hast,
(4)aus dem Inneren von 1 reiße heraus: 30′ ist die Gegenseite.
Dies ist das Problem, das auf Seite
Auch wenn wir diese Aufgabe von diesem Gesichtspunkt aus gut kennen, wollen wir den Text und die Terminologie noch einmal genau untersuchen, um mit ihm auch aus der Perspektive des Autors umgehen zu können.
In Zeile 1 wird die Aufgabe
„Fläche“ und „Gegenseite“ sind angehäuft.
Diese Addition muss benutzt werden, wenn verschiedenartige Größen im
Spiel sind, hier eine Fläche (zwei Dimensionen) und eine Seite (eine Dimension).
Der Text gibt die Summe der beiden Größen, also ihrer Maßzahlen: 45′.
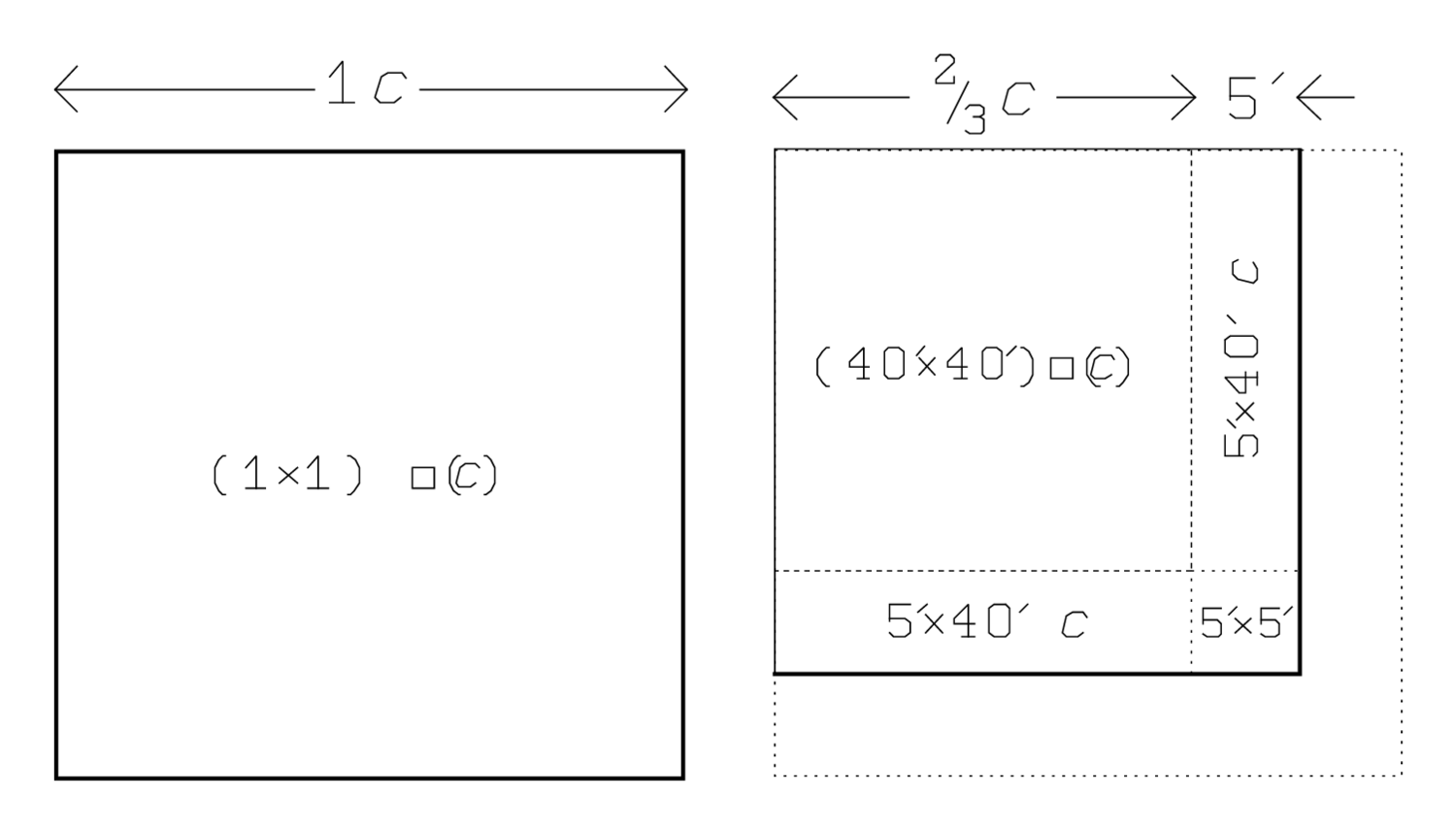
Wenn c für die Seite des Quadrats und
 (c) für dessen Fläche steht, dann kann das
Problem wie folgt in Symbolen ausgedrückt werden:
(c) für dessen Fläche steht, dann kann das
Problem wie folgt in Symbolen ausgedrückt werden:
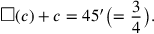
|
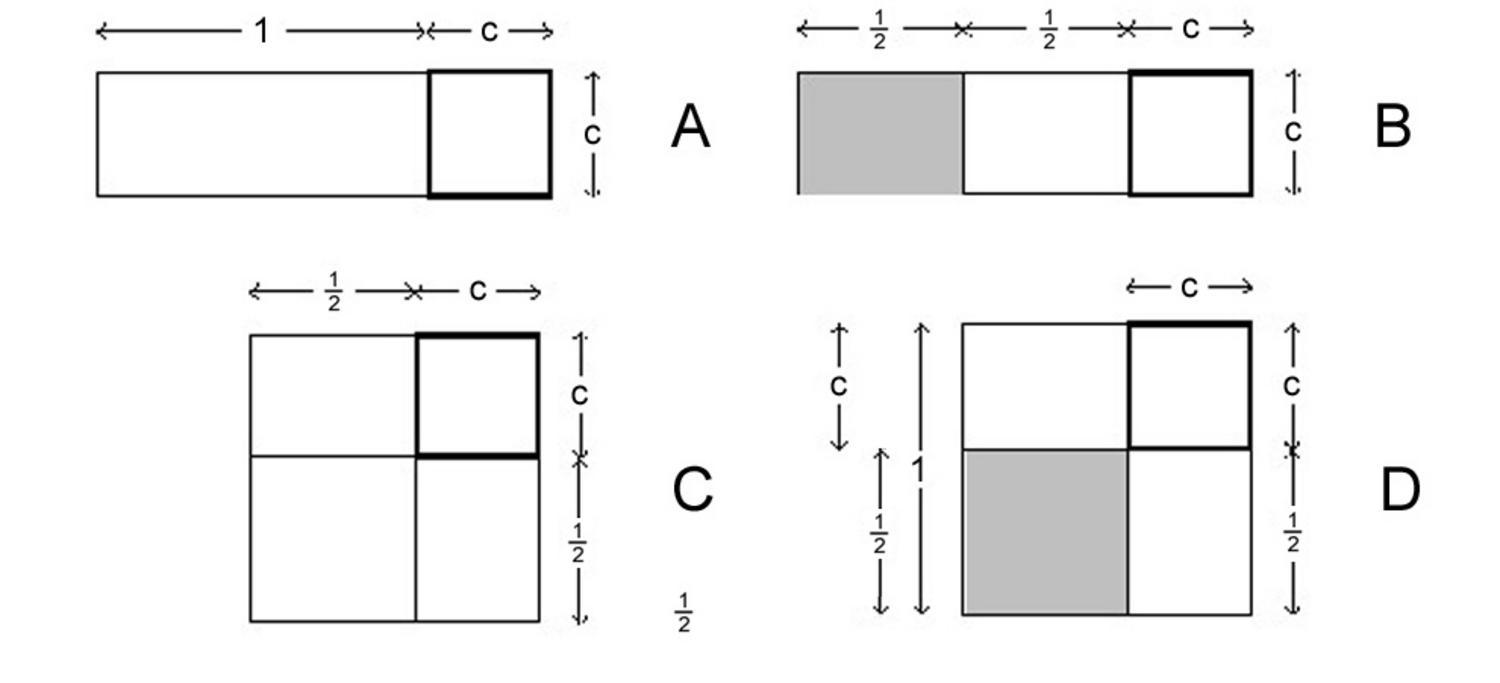
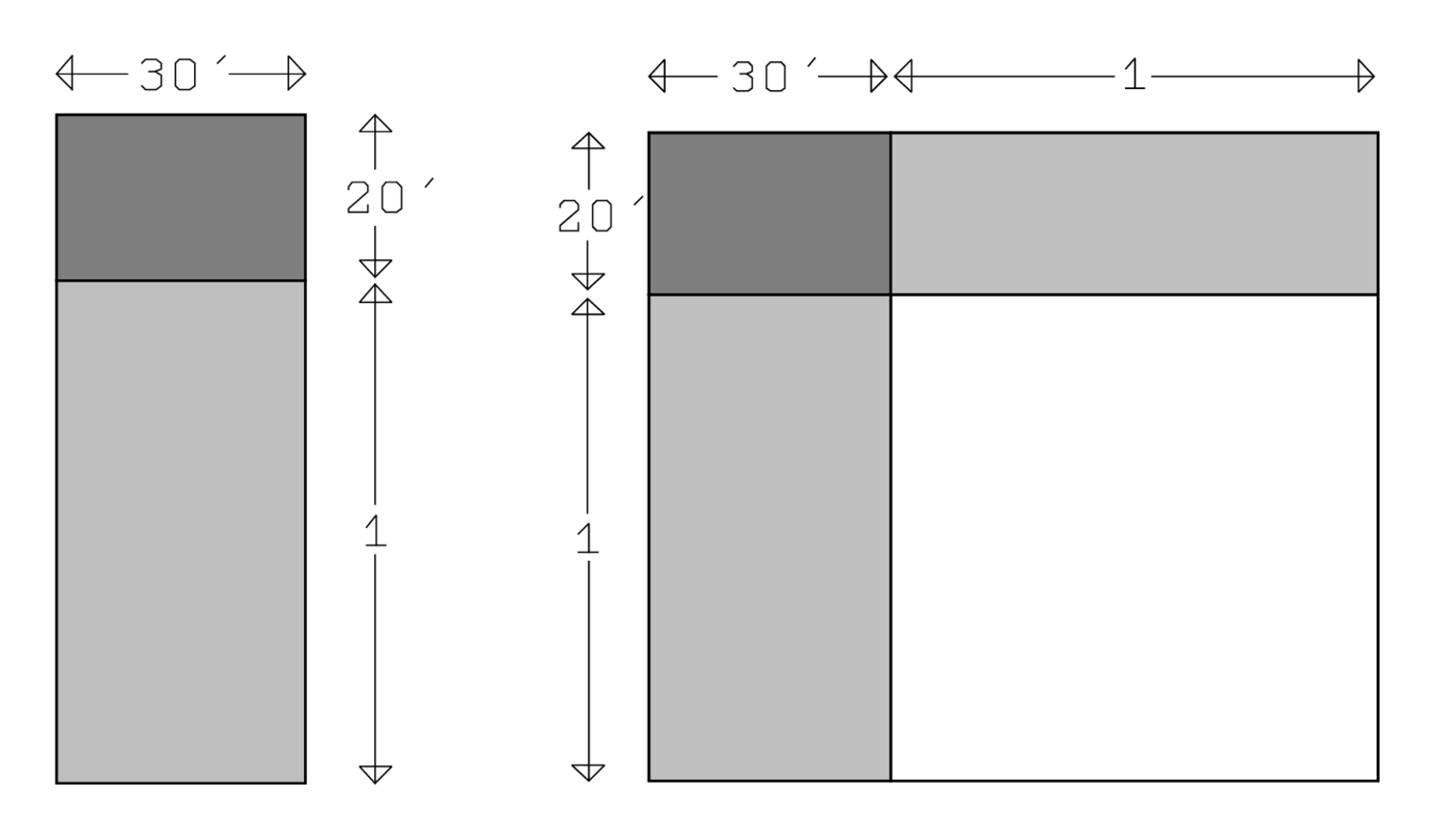
Abb. 3.1: Das Verfahren von BM 13901 #1, in leicht veränderten Proportionen.
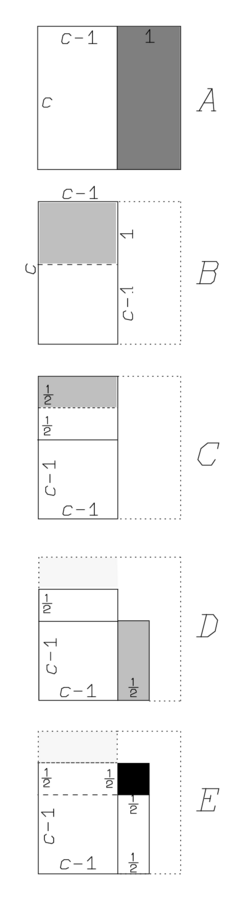
Abbildung 3.1 zeigt die einzelnen Schritte des Verfahrens wie sie im Text erklärt sind:
A. 1, die Projektion, setzt Du. Dies bedeutet, dass ein Rechteck
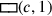 neben das Quadrat
neben das Quadrat
 (c)
gezeichnet wird.
(c)
gezeichnet wird.
Dadurch erhält die Summe einer Länge und einer Fläche,
was per se sinnlos ist, eine geometrische Bedeutung als rechteckige
Fläche
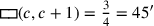 . Diese geometrische
Interpretation erklärt das Auftauchen der „Projektion“
. Diese geometrische
Interpretation erklärt das Auftauchen der „Projektion“
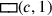 aus dem Quadrat
heraus verläuft wie eine Projektion aus einem Gebäude. Wir erinnern daran (siehe Seite
aus dem Quadrat
heraus verläuft wie eine Projektion aus einem Gebäude. Wir erinnern daran (siehe Seite
B. Das Halbe von 1 brich ab. Die „Projektion“ mit dem
angrenzenden Rechteck
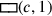 wird in zwei
„natürliche“ Hälften zerbrochen.
wird in zwei
„natürliche“ Hälften zerbrochen.
C. 30′ und 30′ lass enthalten.
Die äußere Hälfte der Projektion (grau gefärbt) wird so bewegt,
dass seine beiden Teile (jedes mit Länge 30′) das Quadrat
mit gepunktetem Rand unten links „enthalten“. Dieses
cut-and-paste-Verfahren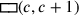 in ein „Gnomon“
zu verwandeln, also ein Quadrat, dem in einer Ecke ein kleineres
Quadrat fehlt.
in ein „Gnomon“
zu verwandeln, also ein Quadrat, dem in einer Ecke ein kleineres
Quadrat fehlt.
D. 15′ zu 45′ fügst Du hinzu: 1.
15′ ist die Fläche des Quadrats, das von den beiden Hälften
(30′ und 30′) gehalten wird, und 45′
die des Gnomon. Wie wir von Seite 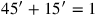 .
.
Bei 1, 1 ist gleich. Im allgemeinen bedeutet die Phrase
„bei Q, s ist gleich“ (siehe
Seite 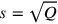 ). Im vorliegenden Fall
sagt uns der Text also, dass die Seite des vervollständigten Quadrats
gleich 1 ist, wie es in D links vom Quadrat angezeigt ist.
). Im vorliegenden Fall
sagt uns der Text also, dass die Seite des vervollständigten Quadrats
gleich 1 ist, wie es in D links vom Quadrat angezeigt ist.
30′, welche Du enthalten lassen hast, aus dem Inneren
von 1 reiße heraus. des ursprünglichen Quadrats zu finden, müssen wir jetzt das Stück
der Länge
des ursprünglichen Quadrats zu finden, müssen wir jetzt das Stück
der Länge
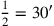 entfernen, welches wir darunter
angefügt haben. „Reiße a aus H heraus“,
ist, wie wir auf Seite
entfernen, welches wir darunter
angefügt haben. „Reiße a aus H heraus“,
ist, wie wir auf Seite
30′ die Gegenseite. Entfernen wir von 1 die
Strecke
 , die wir hinzugefügt hatten,
dann erhalten wir die ursprüngliche Seite c, die
„Gegenseite“, die folglich gleich
, die wir hinzugefügt hatten,
dann erhalten wir die ursprüngliche Seite c, die
„Gegenseite“, die folglich gleich
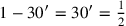 (ganz links D).
(ganz links D).
Dies löst das Problem. In dieser geometrischen Interpretation werden nicht nur die auftretenden Zahlen erklärt, sondern auch die Wörter und Erklärungen, die im Text benutzt werden.
Was die neue Übersetzung angeht sind einige Beobachtungen angebracht.
Wir bemerken, dass kein explizites Argument gegeben ist, wonach die
cut-and-paste-Methode
Der wesentliche Schritt in der altbabylonischen Methode ist die
Ergänzung des Gnomons wie in Abb. 3.2 gezeigt.
Diesen Schritt nennen wir eine „quadratische
Ergänzung“
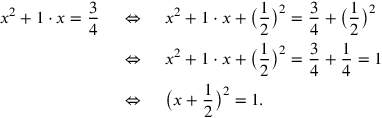
|
Der Name scheint jedoch noch besser zum geometrischen Verfahren zu passen.
Offensichtlich würde eine negative Lösung in dieser konkreten
Interpretation nicht sinnvoll sein. Altbabylonische
Algebra
Einige allgemeine Darstellungen der Geschichte der Mathematik
behaupten, dass die Babylonier negative Zahlen gekannt haben.
Dies ist eine Legende, die auf schlampigem Lesen beruht. Wie
wir bereits gesagt haben, behaupten manche Texte aus stilistischen
Gründen nicht, dass eine Größe A eine andere um den Betrag
d übertrifft, sondern dass B um d
kürzer ist als A; wir werden in
BM 13901 #10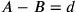 bzw.
bzw.
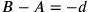 ausgedrückt;
ausgedrückt;
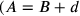 bzw.
bzw.
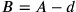 wären näher an den alten
Texten gewesen, aber auch Neugebauer hatte seine stilistischen
Gründe). Auf diese Art haben Mathematiker, welche nur die Übersetzung
in Formeln gelesen haben und nicht die Erklärungen ihrer Bedeutung
(und schon gar nicht die übersetzten Texte), ihre „babylonischen“
negativen
wären näher an den alten
Texten gewesen, aber auch Neugebauer hatte seine stilistischen
Gründe). Auf diese Art haben Mathematiker, welche nur die Übersetzung
in Formeln gelesen haben und nicht die Erklärungen ihrer Bedeutung
(und schon gar nicht die übersetzten Texte), ihre „babylonischen“
negativen
Wie der französische Orientalist Léon Rodet 1881 geschrieben hat, als er modernisierende Interpretationen eines alten ägyptischen mathematischen Papyrus kritisierte:
Um die Geschichte einer Wissenschaft zu studieren, ebenso wie wenn man etwas bekommen will, ist es besser, sich direkt an Gott zu wenden als an seine Heiligen.1
BM 13901 #2
Vs. I
(5)Meine Gegenseite aus der Fläche habe ich herausgerissen: 14‵30 ist es. 1, die Projektion,
(6)setzt Du. Das Halbe von 1 brichst Du, 30′ und 30′ lässt Du enthalten,
(7)15′ zu 14‵30 fügst Du hinzu: bei 14‵30°15′, 29°30′ ist gleich.
(8)30′, welches Du enthalten lassen hast, zu 29°30′ füge hinzu: 30 die Gegenseite.
Dieses Problem, auf einer Tafel mit insgesamt 24 Aufgaben, welche sich auf immer raffiniertere Art und Weise um eines oder mehrere Quadrate drehen, folgt unmittelbar auf dasjenige, das wir eben besprochen haben.
Vom altbabylonischen Standpunkt aus betrachtet ebenso wie von unserem
ist es ein „natürliches“ Gegenstück. Wo das vorherige Problem
„hinzufügt“,
Zu Beginn (Zeile 5) wird das Problem formuliert: Meine Gegenseite aus der Fläche habe ich herausgerissen: 14‵30 ist es. Einmal mehr geht es also um die Fläche eines Quadrats und seine Seite, aber dieses Mal ist die Gegenseite c „herausgerissen“.
Das „Herausreißen“ 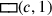 verwandelt, das im
Innern des Quadrats sitzt. Dieses Rechteck (dunkelgrau schattiert)
muss daher „herausgerissen“ werden; was bleibt, nachdem
wir
verwandelt, das im
Innern des Quadrats sitzt. Dieses Rechteck (dunkelgrau schattiert)
muss daher „herausgerissen“ werden; was bleibt, nachdem
wir
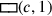 aus
aus
 (c) eliminiert haben,
soll 14‵30 sein. In moderner Symbolsprache entspricht
das Problem also
(c) eliminiert haben,
soll 14‵30 sein. In moderner Symbolsprache entspricht
das Problem also
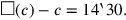
|
Einmal mehr haben wir jetzt ein Rechteck, von dem wir
den Flächeninhalt (14‵30) und die Differenz zwischen
der Länge (c) und der Breite (
 ) kennen –
und wieder einmal ist diese Differenz gleich 1, also der
„Projektion“
) kennen –
und wieder einmal ist diese Differenz gleich 1, also der
„Projektion“
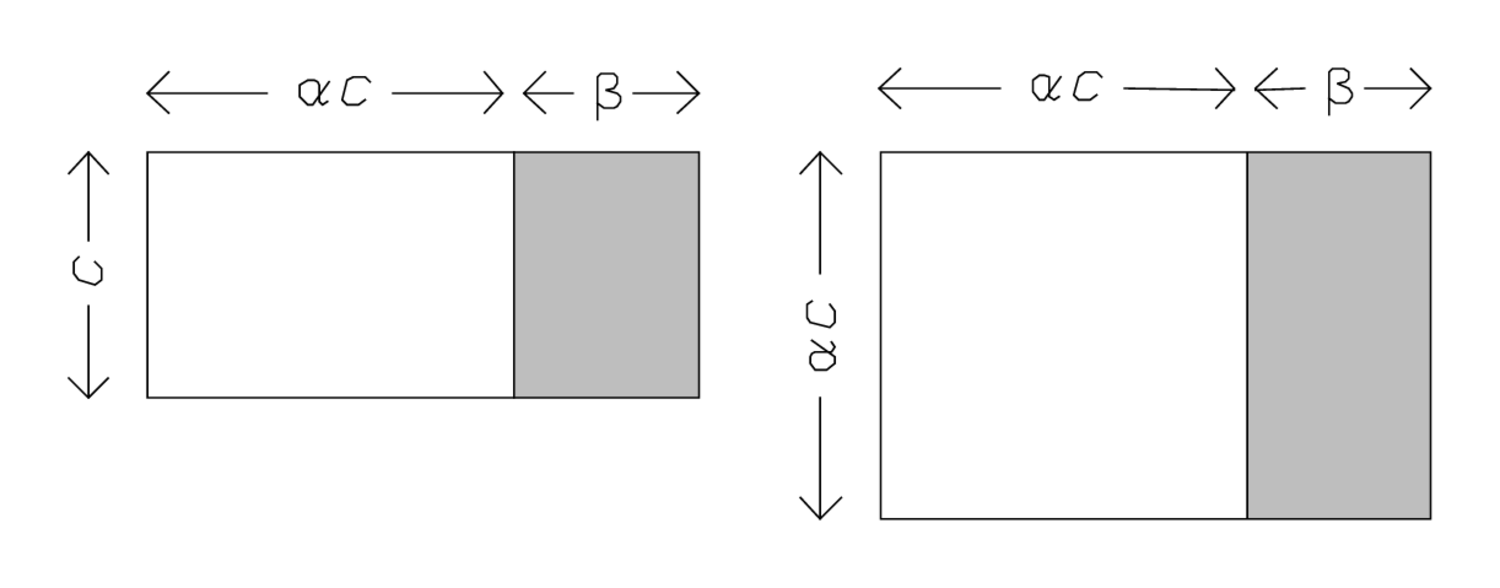
1, die Projektion, setzt Du. In Abb. 3.3, B, besteht
das Rechteck
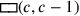 aus einem (weißen) Quadrat und einem
(schattierten) „überschüssigen“ Rechteck, dessen Breite
gleich der Projektion 1 ist.
aus einem (weißen) Quadrat und einem
(schattierten) „überschüssigen“ Rechteck, dessen Breite
gleich der Projektion 1 ist.
Das Halbe von 1 brichst Du. Das überschüssige Rechteck, dargestellt durch seine Breite 1, wird in zwei “Halbe“ geteilt; die Halbe, welche abgetrennt wird, ist in Abb. 3.3, C, schattiert.
Durch cut-and-paste, wie in Abb. 3.3, D gezeigt, erhalten wir
wieder ein Gnomon mit derselben Fläche wie die des Rechtecks
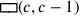 ,
also 14‵30.
,
also 14‵30.
30′ und 30′ lässt Du enthalten, 15′.
Das Gnomon wird durch ein kleines Quadrat (schwarz in Abb. 3.3, E)
ergänzt, welches von den beiden Halben „gehalten“ wird.
Die Fläche dieses vervollständigten Quadrats
Als nächstes werden die Fläche des vervollständigten Quadrats und seine Seite bestimmt: 15′ zu 14‵30 füge hinzu: bei 14‵30°15′, 29°30′ ist gleich.
Indem wir das „Halbe“, das bewegt worden ist, zurücklegen,
finden wir die Seite des ursprünglichen Quadrats zu
 : 30′, welches
Du enthalten lassen hast, zu 29°30′ füge hinzu: 30 die Gegenseite.
: 30′, welches
Du enthalten lassen hast, zu 29°30′ füge hinzu: 30 die Gegenseite.
Wir bemerken das dieses Mal die „Gegenseite“
Wir bemerken ebenfalls, dass das Paar
(14‵30°15′, 29°30′)
nicht in Tabellen von Quadratzahlen und Quadratwurzeln
aufgeführt ist (siehe Seite
YBC 6967
Vs.
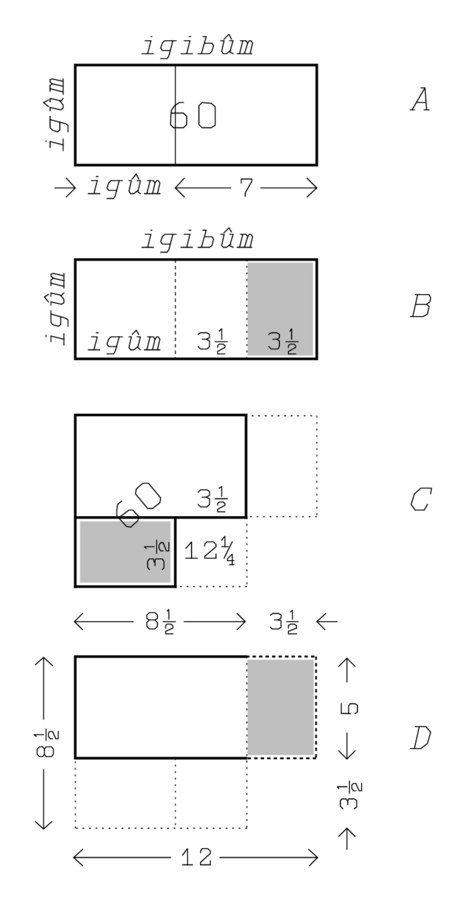
(1)Das igibûm über das igûm, 7 geht es hinaus
(2)igûm und igibûm was?
(3)Du, 7 welches das igibûm
(4)über das igûm hinausgeht,
(5)brich es entzwei: 3°30′;
(6)3°30′ zusammen mit 3°30′
(7)lasse enthalten: 12°15′.
(8)Zu 12°15′ welches für Dich herauskommt,
(9)1‵ die Fläche füge hinzu: 1‵12°15′.
(10)Das Gleiche von 1‵12°15′ was? 8°30′.
(11)8°30′ und 8°30′, die Gegenseite, lege nieder.
Rs.
(1)3°30′, was Du halten lassen hast,
(2)von Eins reiße aus,
(3)zu Eins füge hinzu.
(4)Das erste ist 12, das zweite ist 5.
(5)12 ist das igibûm, 5 ist das igûm.
Probleme zweiten Grades,
Die obige Übung gehört zu letzterem Typ – wenn wir von der Tatsache absehen,
dass es dabei gar nicht um ein Rechteck geht, sondern um ein Zahlenpaar, das in
einer Tabelle von Reziproken steht
Man könnte erwarten, dass das Produkt von igûm and
igibûm
Es ist wichtig zu bemerken, dass hier die „fundamentale Darstellung“
Wie in den beiden analogen vorhergehenden Fällen wird das Rechteck
in ein Gnomon verwandelt, und wie üblich wird das Gnomon zu einem
Quadrat vervollständigt,
Die nächsten Schritte sind bemerkenswert.
Die „Halbe“, die abgebrochen und bei der Bildung des
Gnomons verschoben wurde (das, was das vervollständigende Quadrat
„enthalten lässt“) wird zurück an seinen Platz gesetzt.
Weil es um dasselbe Stück geht, muss es grundsätzlich
verfügbar sein, bevor es „hinzugefügt“ werden kann.
Dies hat zwei Konsequenzen. Zum einen muss
das „Gleiche“
In BM 13901 #1
BM 13901 #10
Vs. II
(11)Die Flächen meiner beiden Gegenseiten habe ich angehäuft: 21°15′.
(12)Gegenseite von Gegenseite, ein Siebtel ist es kleiner geworden.
(13)7 und 6 schreibst Du ein. 7 und 7 lasse enthalten, 49.
(14)6 und 6 lasse enthalten, 36 und 49 häufe an:
(15)1‵25. igi 1‵25 wird nicht abgespalten. Was zu 1‵25
(16)soll ich setzen das mir 21°15′ gibt? Bei 15′, 30′ ist gleich.
(17)30′ zu 7 erhöhst Du: 3°30′ die erste Gegenseite.
(18)30′ zu 6 erhöhst Du: 3 die zweite Gegenseite.
Wir kehren nun zu der Tafel zurück, welche eine Sammlung von Aufgaben
über Quadrate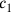 bzw.
bzw.
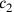 bezeichnet
werden, so:
bezeichnet
werden, so:
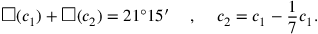
|
In anderen Worten ist das Verhältnis der beiden Seiten wie 7 zu 6.
Dies eröffnet die Möglichkeit einer Lösung durch einen
„falschen Ansatz“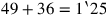 ist. Die Aufgabenstellung verlangt aber,
dass diese Summe gleich 21°15′ sein soll; also muss
die Fläche um einen Faktor 21°15′/1‵25
reduziert werden. Jetzt ist 1‵25 aber keine
„reguläre“ Zahl (siehe Seite
ist. Die Aufgabenstellung verlangt aber,
dass diese Summe gleich 21°15′ sein soll; also muss
die Fläche um einen Faktor 21°15′/1‵25
reduziert werden. Jetzt ist 1‵25 aber keine
„reguläre“ Zahl (siehe Seite 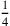 ) angegeben wird. Wenn aber die Fläche um
einen Faktor 15′ reduziert wird, dann müssen die
entsprechenden Seiten um einen Faktor 30′ reduziert werden:
Bei 15′, 30′ ist gleich.
Zum Schluss bleibt noch (Zeilen 17 und 18) 7 und 6 auf 30′
„zu erhöhen“.
) angegeben wird. Wenn aber die Fläche um
einen Faktor 15′ reduziert wird, dann müssen die
entsprechenden Seiten um einen Faktor 30′ reduziert werden:
Bei 15′, 30′ ist gleich.
Zum Schluss bleibt noch (Zeilen 17 und 18) 7 und 6 auf 30′
„zu erhöhen“.
Die erste „Gegenseite“ ist daher
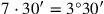 , die
zweite
, die
zweite
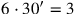 .5
.5
BM 13901 #14
Vs. II
(44)Die Flächen meiner beiden Gegenseiten habe ich angehäuft: 25′25″.
(45)Die [andere] Gegenseite, zwei Drittel der Gegenseite und 5′ nindan.
(46)1 und 40′ und 5′ gehend über 40′ schreibe ein.
(47)5′ und 5′ lasse enthalten, 25″ aus 25′25″ reißt Du heraus:
Rs. I
(1)25′ schreibst Du ein. 1 und 1 lässt Du enthalten: 1. 40′ und 40′ lässt Du enthalten,
(2)26′40″ zu 1 fügst Du hinzu: 1°26′40″ auf 25′ erhöhst Du:
(3)36′6″40‴ schreibst Du ein. 5′ zu 40′ erhöhst Du: 3′20″
(4)und 3′20″ lässt Du enthalten, 11″6‴40⁗ zu 36′6″40‴ fügst Du hinzu:
(5)bei 36′17″46‴40⁗, 46′40″ ist gleich. 3′20″, welches Du enthalten lassen hast,
(6)aus 46′40″ reißt Du heraus: 43′20″ schreibst Du ein.
(7)igi 1°26′40″ wird nicht abgespalten. Was zu 1°26′40″
(8)soll ich setzen das mir 43′20″ gibt? 30′ ist sein bandûm.
(9)30′ zu 1 erhöhst Du: 30′ die erste Gegenseite.
(10)30′ zu 40′ erhöhst Du: 20′, und 5′ fügst Du hinzu:
(11)25′ die zweite Gegenseite.
Auch bei diesem Problem geht es um zwei Quadrate (Zeilen Vs. II.44–45).6
Die etwas obskure Formulierung in Zeile 45 bedeutet, dass die zweite
„Gegenseite“ zwei Drittel der ersten ausmacht, mit zusätzlichen
5′ nindan. Wenn
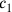 und
und
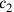 für die
beiden „Gegenseiten“ stehen, dann sagt uns Zeile 44, dass die Summe
der Flächen
für die
beiden „Gegenseiten“ stehen, dann sagt uns Zeile 44, dass die Summe
der Flächen
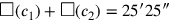 ist, während Zeile 45
angibt, dass
ist, während Zeile 45
angibt, dass
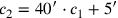 ist.
ist.
Dieses Problem kann nicht durch einen einfachen falschen Ansatz gelöst werden,
bei dem eine Zahl vorläufig als der Wert der Unbekannten angenommen wird –
dies funktioniert nur für homogene Probleme.7
Die Zahlen 1 und 40′ in Zeile 46 zeigen uns den tatsächlich
eingeschlagenen Weg:
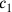 und
und
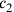 werden durch eine
neue Größe ausgedrückt, welche wir
werden durch eine
neue Größe ausgedrückt, welche wir
 nennen können:
nennen können:
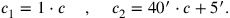
|
Dies entspricht Abb. 3.6. Es zeigt, wie das Problem auf ein
einfacheres reduziert wird, in dem es um ein einziges Quadrat
 geht. Es ist klar, dass die Fläche des ersten der beiden ursprünglichen Quadrate
(
geht. Es ist klar, dass die Fläche des ersten der beiden ursprünglichen Quadrate
(
 ) gleich
) gleich
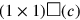 ist, aber diese
Rechnung muss bis Zeile Rs. I.1. warten.
ist, aber diese
Rechnung muss bis Zeile Rs. I.1. warten.
Der Text beginnt mit der Betrachtung von
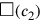 , was
komplizierter ist und zu mehreren Beiträgen Anlass gibt. Zuerst geht es um
das Quadrat
, was
komplizierter ist und zu mehreren Beiträgen Anlass gibt. Zuerst geht es um
das Quadrat
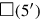 in der rechten unteren Ecke:
5′ und 5′ lasse enthalten,
in der rechten unteren Ecke:
5′ und 5′ lasse enthalten,
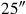 . Dieser Beitrag wird aus der Summe
. Dieser Beitrag wird aus der Summe
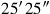 der beiden Flächen eliminiert:
der beiden Flächen eliminiert:
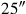 aus
aus
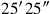 reiße heraus: 25′ schreibe ein. Die verbleibenden 25′
müssen nun in Abhängigkeit der Fläche und der Seite des neuen
Quadrats
reiße heraus: 25′ schreibe ein. Die verbleibenden 25′
müssen nun in Abhängigkeit der Fläche und der Seite des neuen
Quadrats
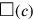 erklärt werden.
erklärt werden.
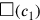 ist, wie schon gesagt,
ist, wie schon gesagt,
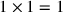 mal die Fläche
mal die Fläche
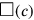 :
1 und 1 lasse enthalten: 1.8 Nach der Elimination der Ecke
:
1 und 1 lasse enthalten: 1.8 Nach der Elimination der Ecke
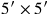 bleibt von
bleibt von
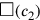 einerseits ein Quadrat
einerseits ein Quadrat
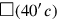 übrig, andererseits zwei „Flügel“, auf die wir gleich
zurückkommen werden. Die Fläche des Quadrats
übrig, andererseits zwei „Flügel“, auf die wir gleich
zurückkommen werden. Die Fläche des Quadrats
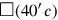 ist
ist
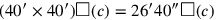 :
40′ und 40′ lasse enthalten, 26′40″. Insgesamt haben wir also das
:
40′ und 40′ lasse enthalten, 26′40″. Insgesamt haben wir also das
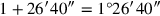 -fache der Quadratfläche
-fache der Quadratfläche
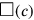 : 26′40″ zu 1 füge hinzu: 1°26′40″.
: 26′40″ zu 1 füge hinzu: 1°26′40″.
Jeder „Flügel“ ist ein Rechteck
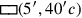 ,
mit der Fläche
,
mit der Fläche
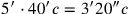 :
5′ auf 40′ erhöhe: 3′20″.
:
5′ auf 40′ erhöhe: 3′20″.
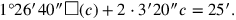
|
Diese Gleichung stellt uns vor ein Problem, welches der altbabylonische Autor
schon in Zeile Rs. I.2 vorhergesehen hat, und das ihn dazu bewegt hat,
die Berechnung der Flügel auf später zu verschieben. Wir würden heute sagen,
die Gleichung sei nicht „normalisiert“, weil der Koeffizient
des quadratischen Terms nicht gleich 1 ist. Der altbabylonische Rechner
hätte dies erklären können, indem er in der Terminologie von
TMS XVI Quadratflächen
(das weiße Rechteck
Quadratflächen
(das weiße Rechteck
 ) und von
) und von
 Seiten
haben, also das schattierte Rechteck
Seiten
haben, also das schattierte Rechteck
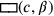 , was der Gleichung
, was der Gleichung
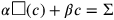
|
entspricht (im vorliegenden Fall ist
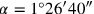 ,
,
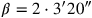 , und
, und
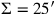 ). Dies
hindert uns daran, unsere gewohnte cut-and-paste-Methode
). Dies
hindert uns daran, unsere gewohnte cut-and-paste-Methode
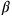 und das Enthaltenlassen der beiden Halben würde
uns kein Gnomon geben.
und das Enthaltenlassen der beiden Halben würde
uns kein Gnomon geben.
Die Babylonier umgingen diese Schwierigkeit mit Hilfe eines Tricks,
der auf der rechten Seite von Abb. 3.7 zu sehen ist: Der
Maßstab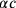 statt
statt
 wird.
wird.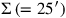 ,
sondern
,
sondern
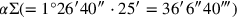 :
1°26′40″ auf 25′ erhöhe: 36′6″40‴ schreibe ein. Wir wir sehen, hat sich die Zahl
:
1°26′40″ auf 25′ erhöhe: 36′6″40‴ schreibe ein. Wir wir sehen, hat sich die Zahl
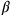 der Seiten nicht geändert,
sondern nur der Wert der Seite, der von
der Seiten nicht geändert,
sondern nur der Wert der Seite, der von
 zu
zu
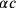 geworden ist.9
geworden ist.9
In moderner Symbolsprache entspricht diese Umformung der Multiplikation beider Seiten der Gleichung
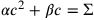
|
mit
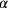 , und dies gibt uns die normalisierte Gleichung
, und dies gibt uns die normalisierte Gleichung
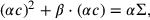
|
in der Unbekannten
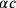 .
.
Eine Gleichung dieses Typs ist uns schon in
BM 13901 #1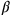 bestimmen). Wie wir schon gesagt haben,
trägt jeder „Flügel“ 5′40″=3′20″ Seiten bei.
Hätte der Rechner mechanisch nach festen Algorithmen gearbeitet, hätte er
nun mit 2 multipliziert, um
bestimmen). Wie wir schon gesagt haben,
trägt jeder „Flügel“ 5′40″=3′20″ Seiten bei.
Hätte der Rechner mechanisch nach festen Algorithmen gearbeitet, hätte er
nun mit 2 multipliziert, um
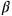 zu finden. Aber er tut es nicht!
Er weiß in der Tat, dass die beiden Flügel den Überschuss darstellen, der
in zwei „Halbe“ „zerbrochen“ werden muss.
Er lässt daher 3′20″ und 3′20″
„enthalten“, was die quadratische Ergänzung liefert, und
„fügt“ die sich ergebende Fläche 11″6‴40⁗ zu der Fläche
36′6″40‴ des Gnomons hinzu: 3′20″ und 3′20″
lasse enthalten, 11″6‴40⁗ zu 36′6″40‴ füge hinzu [...]
36′17″46‴40⁗.
zu finden. Aber er tut es nicht!
Er weiß in der Tat, dass die beiden Flügel den Überschuss darstellen, der
in zwei „Halbe“ „zerbrochen“ werden muss.
Er lässt daher 3′20″ und 3′20″
„enthalten“, was die quadratische Ergänzung liefert, und
„fügt“ die sich ergebende Fläche 11″6‴40⁗ zu der Fläche
36′6″40‴ des Gnomons hinzu: 3′20″ und 3′20″
lasse enthalten, 11″6‴40⁗ zu 36′6″40‴ füge hinzu [...]
36′17″46‴40⁗.
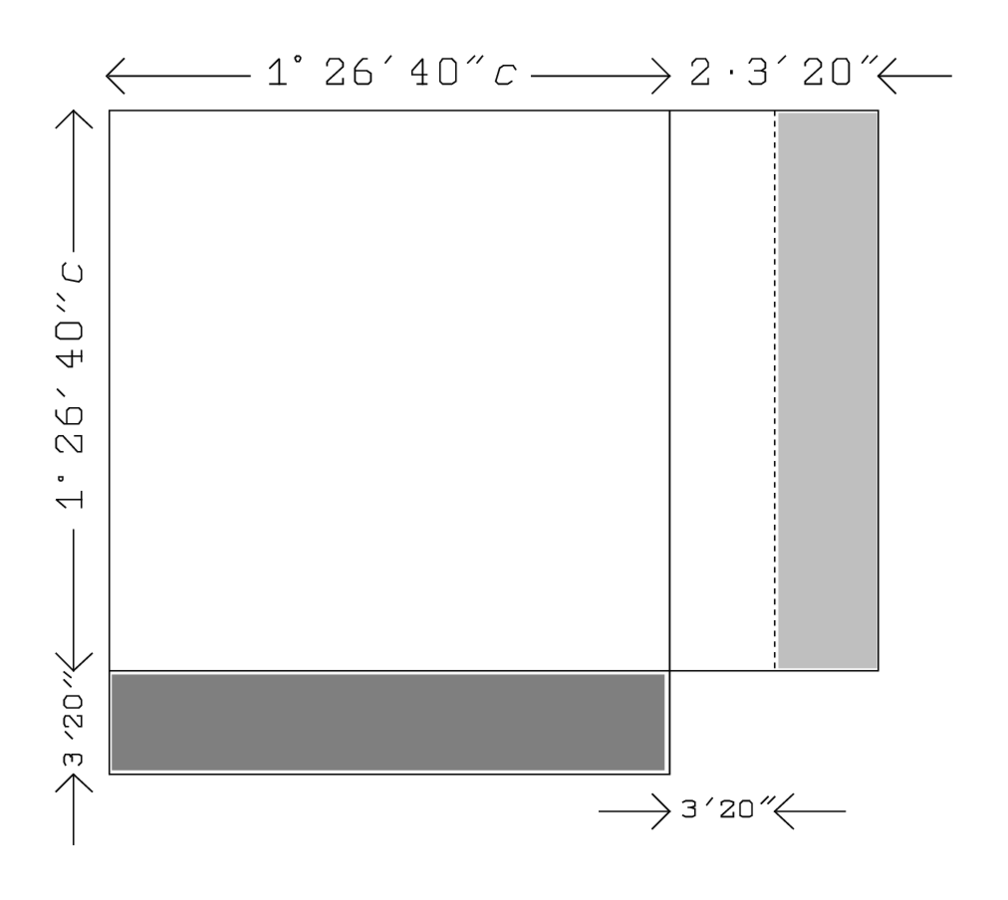
Abb. 3.8: BM 13901 #14, das normalisierte Problem.
36′17″46‴40⁗ ist daher die Fläche des
vervollständigten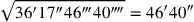 :
bei 36′17″46‴40⁗, 46′40″ ist gleich.
Diese Zahl stellt
:
bei 36′17″46‴40⁗, 46′40″ ist gleich.
Diese Zahl stellt
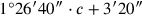 dar;
dar;
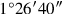
 ist folglich
ist folglich
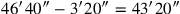 :
3′20″, das du enthalten lassen hast, aus
46′40″ reiße heraus: 43′20″ schreibe ein.
Als nächstes müssen wir den Wert von c finden.
1°26′40″ ist eine irreguläre Zahl, und der Quotient
:
3′20″, das du enthalten lassen hast, aus
46′40″ reiße heraus: 43′20″ schreibe ein.
Als nächstes müssen wir den Wert von c finden.
1°26′40″ ist eine irreguläre Zahl, und der Quotient
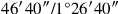 wird direkt als 30′
angegeben:10
igi 1°26′40″ wird nicht abgespalten. Was soll ich
zu 1°26′40″ setzen, das mir 43′20″ gibt? 30′, sein bandûm.
Zum Schluss werden
wird direkt als 30′
angegeben:10
igi 1°26′40″ wird nicht abgespalten. Was soll ich
zu 1°26′40″ setzen, das mir 43′20″ gibt? 30′, sein bandûm.
Zum Schluss werden
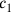 und
und
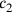 bestimmt,
bestimmt,
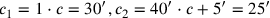 :11
30′ auf 1 erhöhe: 30′ die erste Gegenseite.
30′ auf 40′ erhöhe: 20′, und 5′
füge hinzu: 25′ die zweite Gegenseite. Die Aufgabe ist gelöst.
:11
30′ auf 1 erhöhe: 30′ die erste Gegenseite.
30′ auf 40′ erhöhe: 20′, und 5′
füge hinzu: 25′ die zweite Gegenseite. Die Aufgabe ist gelöst.
TMS IX #1 und #2
#1
(1)Die Oberfläche und 1 die Länge habe ich angehäuft, 40′. ¿30, die Länge,? 20′ die Breite
(2)Als 1 Länge zu 10′ der Fläche wurde hinzugefügt,
(3)oder 1 (als) Basis zu 20′, der Breite, wurde hinzugefügt,
(4)oder 1°20′ ¿ist gesetzt? zur Breite, welche 40′ zusammen mit der Länge ¿hält?
(5)oder 1°20′ zusam⟨men⟩ mit 30′ der Länge enthält, 40′ (ist) dessen Name.
(6)Weil so, zu 20′ der Breite, wie Dir gesagt ist,
(7)1 wird hinzugefügt: 1°20′ siehst Du. Hiervon ausgehend
(8)fragst Du. 40′ die Fläche, 1°20′ die Breite, die Länge was?
(9)30′ die Länge. Dies ist das Verfahren.
#2
(10)Fläche, Länge und Breite habe ich angehäuft, 1. Nach der akkadischen (Methode)
(11)1 zur Länge füge hinzu. 1 zur Breite füge hinzu. Weil 1 zur Länge hinzugefügt ist,
(12)1 zur Breite hinzugefügt ist, 1 und 1 lasse enthalten, 1 siehst Du.
(13)1 zum Haufen von Länge, Breite und Fläche füge hinzu, 2 siehst Du.
(14)Zu 20′, der Breite, 1 füge hinzu, 1°20′. Zu 30′, der Länge, 1 füge hinzu, 1°30′.
(15)¿Weil? eine Fläche, die von Breite 1°20′, von Länge 1°30′,
(16)¿die Länge zusammen mit? der Breite man enthalten lassen hat, was ist ihr Name?
(17)2 die Fläche.
(18)So geht die akkadische (Methode).
Wie TMS XVI #1
Die Abbildung in Abb. 3.9 links ist in Übereinstimmung mit dem Text von #1 gezeichnet, in welchem die Summe der Fläche und der Länge eines Rechtecks gegeben ist. Parallel zu unserer symbolischen Umformung
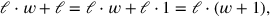
|
wird die Breite mit einer
„Basis“
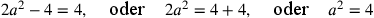
|
schreiben.
Zeile 2 spricht von der „Fläche“ als 10′.
Der Schüler soll also einmal mehr annehmen, dass die Diskussion
sich um das Rechteck
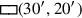 dreht. Die Tafel ist zerbrochen,
weswegen wir nicht wissen, ob die Länge explizit gegeben war; Zeile 6 zeigt
allerdings, dass die Breite gegeben war.
dreht. Die Tafel ist zerbrochen,
weswegen wir nicht wissen, ob die Länge explizit gegeben war; Zeile 6 zeigt
allerdings, dass die Breite gegeben war.
Am Ende zeigen Zeilen 7-9, wie man die Länge findet, wenn die Breite zusammen mit der Summe von Fläche und Länge bekannt ist (durch eine Division, die hier nur implizit durchgeführt wird).
Aufgabe #2 lehrt, wie man sich in einer komplexeren Situation verhält:
Jetzt ist die Summe der Fläche und beider Seiten eines Rechtecks gegeben
(siehe Abb. 3.9 rechts).
Sowohl Länge als auch Breite werden um 1 verlängert; dies erzeugt zwei
Rechtecke
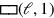 und
und
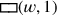 , deren Flächen
die Länge bzw. die Breite darstellen. Aber dies erzeugt auch ein leeres
Eckquadrat
, deren Flächen
die Länge bzw. die Breite darstellen. Aber dies erzeugt auch ein leeres
Eckquadrat
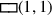 . Ist dieses gefüllt, dann haben wir ein größeres
Rechteck der Länge
. Ist dieses gefüllt, dann haben wir ein größeres
Rechteck der Länge
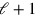 (= 1°30′),
der Breite
(= 1°30′),
der Breite
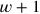 (= 1°20′) und der Fläche
(= 1°20′) und der Fläche
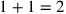 ;
eine Probe bestätigt, dass das Rechteck, das diese beiden Seiten enthalten,
tatsächlich Fläche 2 besitzt.
;
eine Probe bestätigt, dass das Rechteck, das diese beiden Seiten enthalten,
tatsächlich Fläche 2 besitzt.
Diese Methode hat einen Namen, was in der altbabylonischen Mathematik (zumindest
in den uns erhaltenen Texten) sehr selten ist. Sie heißt „die akkadische
(Methode).“
Fußnoten
Léon Rodet, Les prétendus problèmes d'algèbre du manuel du calculateur Égyptien (Papyrus Rhind), Journal asiatique (7) 18 (1881), S. 205.
Auf der anderen
Seite ist die Umkehroperation des
„Anhäufens“ überhaupt keine Subtraktion,
sondern eine Zerlegung in Bestandteile. Siehe Fußnote
3, Seite
Das fragliche Verb (nadûm) hat ein breites Spektrum an Bedeutungen, darunter „zeichnen“ oder „schreiben“ (auf einer Tafel); das Verb lapātum, das wir als „einschreiben“ übersetzen, hat übrigens dieselbe Bedeutung. Weil das, was „niedergelegt“ wird, ein numerischer Wert ist, könnte es scheinen, dass die letztere Interpretation vorzuziehen ist – aber weil geometrische Größen regelmäßig mit ihren numerischen Maßen identifiziert wurden, muss dies nicht zwangsläufig der Fall sein.
Hier sehen wir einen der stilistischen Gründe, der zu einer Formulierung durch Fehlen statt durch Überschuss führt: man hätte genauso gut sagen können, dass die eine Seite die andere um ein Sechstel übertrifft, aber auf dem Gebiet der Multiplikation und des Nehmens von Bruchteilen gaben die Babylonier den Zahlen 4, 7, 11, 13, 14 und 17 einen besonderen Status. Im nächsten Problem dieser Tafel geht es darum,dass eine Seite die andere um ein Siebtel übertrifft, und wieder wäre es möglich gewesen zu sagen, dass die zweite ein Achtel kürzer ist als die erste.
Es wäre denkbar, dass die zugrunde liegende
Idee eine leicht andere ist, dass nämlich die ursprünglichen Quadrate in
7×7 bzw. 6×6 Teilquadrate zerlegt werden,
deren Anzahl insgesamt 1‵25 wäre, von denen dann also jedes
einzelne eine Fläche von
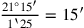 und eine Seite
30′ hätte. Diese Interpretation wird allerdings ausgeschlossen
durch die Operation „enthalten lassen“:
Tatsächlich sind die ursprünglichen Quadrate bereits vorhanden, und es gibt
folglich keinen Grund, sie zu konstruieren (in TMS VIII #1
wird eine Unterteilung in kleinere Teilquadrate vorgenommen, und dort
wird deren Anzahl tatsächlich durch „erhöhen“
gefunden – siehe Seite
und eine Seite
30′ hätte. Diese Interpretation wird allerdings ausgeschlossen
durch die Operation „enthalten lassen“:
Tatsächlich sind die ursprünglichen Quadrate bereits vorhanden, und es gibt
folglich keinen Grund, sie zu konstruieren (in TMS VIII #1
wird eine Unterteilung in kleinere Teilquadrate vorgenommen, und dort
wird deren Anzahl tatsächlich durch „erhöhen“
gefunden – siehe Seite
Dieser Teil der Tafel ist schwer beschädigt. Aufgabe #24 auf derselben Tafel dreht sich um drei Quadrate, verläuft aber sonst streng parallel, und erlaubt so eine unzweifelhafte Rekonstruktion.
Bei einem einfachen
falschen Ansatz wird die vorläufig angenommene Zahl um einen Faktor
reduziert, der dem gefundenen Fehler entspricht; wenn wir aber die Werte
für
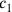 und
und
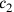 mit einem gewissen Faktor reduzieren,
etwa mit
mit einem gewissen Faktor reduzieren,
etwa mit
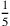 , dann würde das zusätzliche 5′
ebenfalls um diesen Faktor reduziert, also auf 1′. Nach der Reduktion
würden wir daher
, dann würde das zusätzliche 5′
ebenfalls um diesen Faktor reduziert, also auf 1′. Nach der Reduktion
würden wir daher
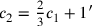 haben.
haben.
Diese sorgfältige Rechnung
zeigt, dass der Autor sich ein neues Quadrat vorstellt,
und nicht
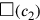 in Abhängigkeit von
in Abhängigkeit von
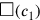 und
und
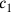 ausdrückt.
ausdrückt.
Dieser Trick wurde bei der Lösung nicht-normalisierter
Gleichungen regelmäßig benutzt, und es gibt keinen Grund anzunehmen, dass
die Babylonier eine bestimmte Darstellung wie in Abb. 3.7
benötigt haben. Sie könnten sich vorstellen, dass der Maßstab
in einer Richtung geändert wurde – wir wissen aus anderen Texten,
dass ihre Diagramme sehr ungenau sein konnten, also bloße
Strukturdiagramme waren – mehr wurde zur Gedankenführung nicht benötigt.
Sie mussten also nur die Summe
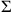 mit
mit
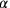 multiplizieren, und dies konnten (und, wie hier, würden) sie tun, bevor sie
multiplizieren, und dies konnten (und, wie hier, würden) sie tun, bevor sie
 ausrechneten.
ausrechneten.
Der Quotient heißt ba.an.da. Dieser sumerische
Ausdruck könnte „das was an die Seite gestellt wird“
bedeuten, was der Art entsprechen könnte, wie Multiplikationen auf einer
Hilfstafel ausgeführt wurden. Siehe die Fußnote 11,
Seite
Dass der Wert von c1 als 1⋅c berechnet wird und nicht direkt mit c identifiziert wird bestätigt, dass wir mit einer neuen Seite c gearbeitet haben.
Die Tafel ist ziemlich beschädigt; wir erinnern daran, dass die mit ¿…? gekennzeichneten Abschnitte Rekonstruktionen sind, welche die Bedeutung (die dem Kontext entnommen werden können), aber nicht notwendig den genauen Wortlaut des Originals wiedergeben.
Das Wort ki.gub.gub ist eine Zusammensetzung sumerischer Wörter, welches nicht von andern Tafeln bekannt ist, und das eine ad hoc-Konstruktion sein könnte. Es bezeichnet vermutlich etwas, das stabil auf den Boden gelegt wird.

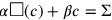 .
.