Im letzten Kapitel haben wir die Methoden vorgestellt, welche die Babylonier für die Lösung der grundlegenden Probleme zweiten Grades benutzt haben: cut-and-paste, quadratische Ergänzung und Maßstabswechsel. Die Babylonier haben allerdings, wie man am Ausdruck „grundlegend“ erkennen kann, auch komplexere Aufgaben bearbeitet. Solche Aufgaben stehen im Mittelpunkt dieses Kapitels, und wir beginnen mit dem dritten Abschnitt des Texts, von dem wir die beiden einführenden pädagogischen Abschnitte bereits untersucht haben.
TMS IX #3
(19)Fläche, Länge und Breite habe ich angehäuft; 1 die Fläche. 3 Längen, 4 Breiten angehäuft,
(20)dessen 17tel zur Breite hinzugefügt, 30′.
(21)Du, 30′ bis 17 gehe: 8°30′ siehst Du.
(22)Zu 17 Breiten füge 4 Breiten hinzu, 21 siehst Du.
(23)21, so viel wie von Breiten, setze. 3, von drei Längen
(24)3, so viel wie von Längen, setze. 8°30′, was ist dessen Name?
(25)3 Längen und 21 Breiten angehäuft.
(26) 8°30′ siehst Du,
(27) 3 Längen und 21 Breiten angehäuft
(28)Weil 1 zur Länge hinzugefügt ist und 1 zur Breite hinzugefügt, lasse enthalten:
(29)1 zum Haufen von Fläche, Länge und Breite füge hinzu, 2 siehst Du,
(30)2 die Fläche. Weil die Länge und die Breite von 2 der Fläche,
(31)1°30′, die Länge, zusammen mit 1°20′, der Breite, sind enthalten gelassen,
(32)1, das Hinzugefügte der Länge, und 1, das Hinzugefügte der Breite,
(33)lasse enthalten, ¿1 siehst Du.? 1 und 1, die verschiedenen (Dinge), häufe an, 2 siehst Du.
(34)3 ..., 21 ..., und 8°30′ häufe an, 32°30′ siehst Du;
(35)so fragst Du.
(36)...der Breiten, zu 21, dem Haufen:
(37)...auf 3, Längen, erhöhe,
(38)1‵3 siehst Du. 1‵3 auf 2, die Fläche, erhöhe:
(39)2‵6 siehst Du, ¿2‵6 die Fläche?. 32°30′ den Haufen breche, 16°15′ ⟨siehst⟩ Du.
(40){…}. 16°15′ die Gegenseite setze, lasse enthalten,
(41)4‵24°3′45″ siehst Du. 2‵6 ¿ aus dem Innern?
(42)von 4‵24°3′45″ reiße heraus, 2‵18°3′45″ siehst Du.
(43)Was ist gleich? 11°45′ ist gleich, 11°45′ zu 16°15′ füge hinzu,
(44)28 siehst Du. Vom 2ten reiße aus,4°30′ siehst Du.
(45)igi 3, von den Längen, spalte ab, 20′ siehst Du. 20′ auf 4°30′
(46){…} erhöhe: 1°30′ siehst Du;
(47)1°30′ die Länge von 2 der Fläche. Was zu 21, der Breite, kann ich setzen
(48)das mir 28 gibt? 1°20′ setze, 1°20′ die Breite
(49)von 2 der Fläche. Gehe zurück. 1 von 1°30′ reiße aus,
(50)30′ siehst Du. 1 von 1°20′ reiße aus,
(51)20′ siehst Du.
Zeilen
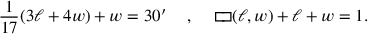
|
In Übereinstimmung mit dem, was wir anderswo gesehen haben, multipliziert
der Text die Gleichung ersten Grades mit 17 (unter Benutzung des akkadischen
Verbs „gehen“,
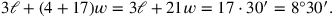
|
Dies wird in den Zeilen 21-25 gemacht, während die Zeilen 26 und 27 das Ergebnis zusammenfassen.
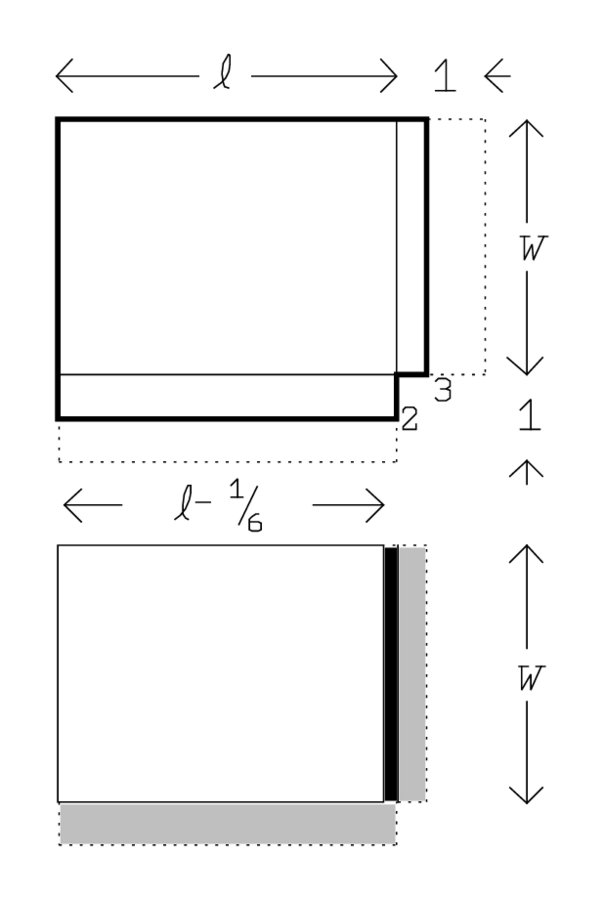
Zeilen 28-30 wiederholen den Trick, der in Abschnitt #2 des Texts
(siehe Abb. 3.9 rechts) schon benutzt wurde: die Länge und die
Breite werden auf 1 verlängert, und das Quadrat, das die beiden
„hinzugefügten“1 Seiten „enthalten“, wird dem „Haufen“
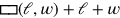 „hinzugefügt“. Dies ergibt eine
„Fläche 2“, deren Bedeutung in den Zeilen 30-33
wieder erklärt wird.
„hinzugefügt“. Dies ergibt eine
„Fläche 2“, deren Bedeutung in den Zeilen 30-33
wieder erklärt wird.
Die Zeilen 34-37 sind sehr beschädigt, zu beschädigt, um sie sicher
rekonstruieren zu können, was die Wortwahl angeht. Allerdings reichen
die Zahlen aus um zu sehen, wie die Rechnungen verlaufen.
Wir wollen die Größen
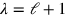 und
und
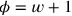 einführen.
Der Text bezieht sich auf diese als die Länge und die Breite „der
Fläche 2“, in anderen Worten:
einführen.
Der Text bezieht sich auf diese als die Länge und die Breite „der
Fläche 2“, in anderen Worten:
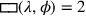 . Weiter
ist
. Weiter
ist
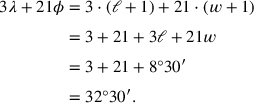
|
Um das Verständnis für das Folgende zu erleichtern, können wir weiter die Variablen
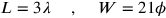
|
einführen (wir müssen allerdings im Auge behalten, dass der Text für diese
keine besonderen Namen hat – im Gegensatz zu
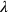 und
und
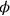 , die solche Namen haben; wir sprechen nun über,
nicht mit dem babylonischen Autor). Zeilen 36-39 finden
, die solche Namen haben; wir sprechen nun über,
nicht mit dem babylonischen Autor). Zeilen 36-39 finden
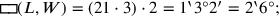
|
zusammenfassend haben wir also
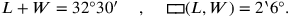
|
Wir sind nun bei Zeile 39 angekommen, und damit bei einem Problem, das wir bisher noch nicht angetroffen haben: Ein Rechteck, von dem wir die Fläche und die Summe der beiden Seiten kennen.
Einmal mehr wird zur cut-and-paste-Methode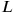 und
und
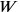 . Dieses Rechteck besteht
aus
. Dieses Rechteck besteht
aus
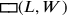 , mit durchgezogenen Linien gezeichnet, und einem Quadrat
, mit durchgezogenen Linien gezeichnet, und einem Quadrat
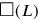 rechts davon, das mit punktierten Seiten gezeichnet ist.
Als nächstes lassen wir die beiden „Halben“ dieser Strecke ein
Quadrat „enthalten“ (Zeilen 39-40). Wie wir sehen,
passt der Teil des ursprünglichen Rechtecks
rechts davon, das mit punktierten Seiten gezeichnet ist.
Als nächstes lassen wir die beiden „Halben“ dieser Strecke ein
Quadrat „enthalten“ (Zeilen 39-40). Wie wir sehen,
passt der Teil des ursprünglichen Rechtecks
 , der außerhalb
des neuen Quadrats liegt, genau in dieses hinein und bildet so zusammen mit dem
Teil, der an seinem Platz geblieben ist, ein Gnomon. In seiner ursprünglichen Lage
erscheint dieser Teil leicht schattiert, in der neuen Lage dagegen dunkel schattiert.
, der außerhalb
des neuen Quadrats liegt, genau in dieses hinein und bildet so zusammen mit dem
Teil, der an seinem Platz geblieben ist, ein Gnomon. In seiner ursprünglichen Lage
erscheint dieser Teil leicht schattiert, in der neuen Lage dagegen dunkel schattiert.
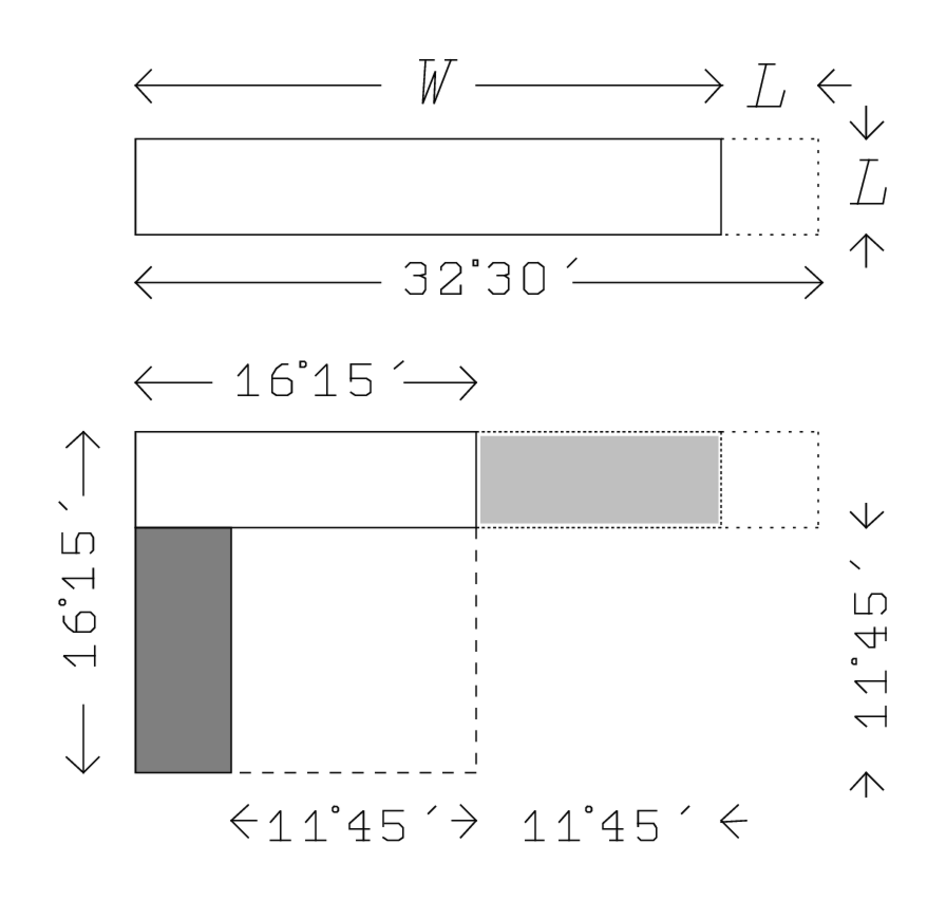
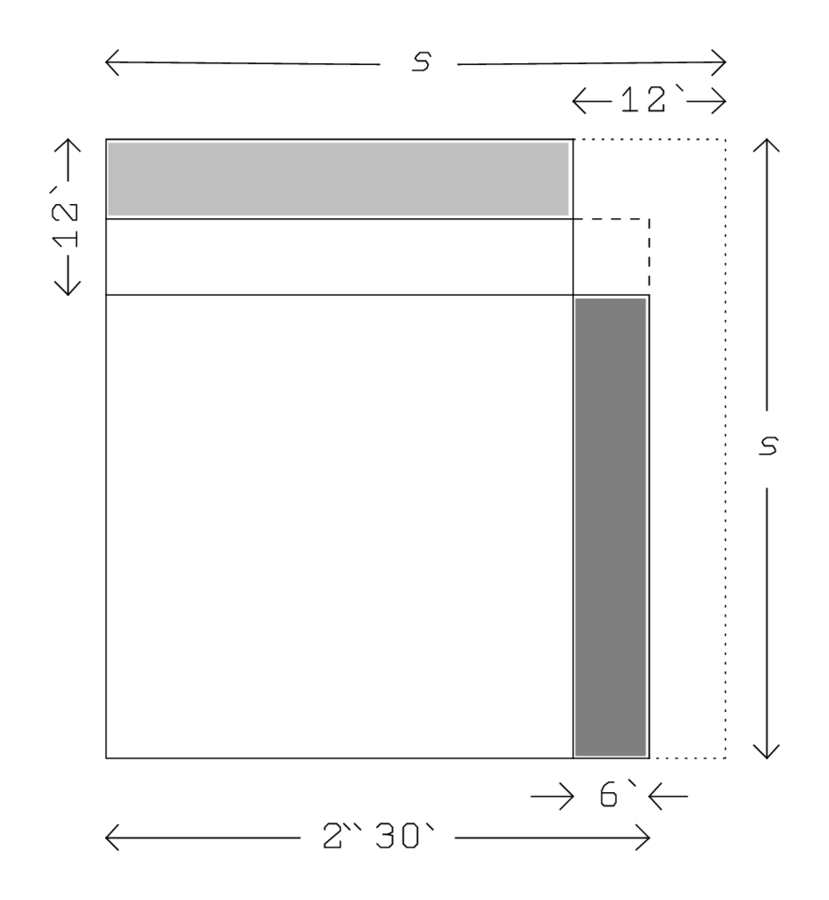
Abb. 4.1: Die cut-and-paste-Methode von TMS IX #3.
Ein Teil des neuen Quadrats
 (16°15′) besteht aus dem Gnomon,
dessen Fläche gleich derjenigen des ursprünglichen Rechtecks
(16°15′) besteht aus dem Gnomon,
dessen Fläche gleich derjenigen des ursprünglichen Rechtecks
 ist; dies Fläche ist daher 2‵6. Wir kennen auch die Fläche des
äußeren Quadrats, nämlich
ist; dies Fläche ist daher 2‵6. Wir kennen auch die Fläche des
äußeren Quadrats, nämlich
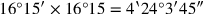 (Zeilen 40 und 41).
Wenn das Gnomon „herausgerissen“ wird (Zeilen 41 und 42), bleibt
2‵18°3′45″ für das Quadrat, das im Gnomon enthalten ist.
Dessen Seite (diejenige, welche „gleich ist“) ist
11°45′, und diese muss nun zu einem der Stücke 16°15′
„hinzugefügt“ (was uns
(Zeilen 40 und 41).
Wenn das Gnomon „herausgerissen“ wird (Zeilen 41 und 42), bleibt
2‵18°3′45″ für das Quadrat, das im Gnomon enthalten ist.
Dessen Seite (diejenige, welche „gleich ist“) ist
11°45′, und diese muss nun zu einem der Stücke 16°15′
„hinzugefügt“ (was uns
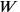 gibt) und
aus dem anderen, seinem „Gegenstück“, „herausgerissen“
werden (was uns
gibt) und
aus dem anderen, seinem „Gegenstück“, „herausgerissen“
werden (was uns
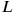 gibt). Dieses Mal wird jedoch nicht
dasselbe Stück „hinzugefügt“ und „herausgerissen“,
und es gibt daher keinen Grund, es „herauszureißen“ bevor es
„hinzugefügt“ wird, wie in
YBC 6967
gibt). Dieses Mal wird jedoch nicht
dasselbe Stück „hinzugefügt“ und „herausgerissen“,
und es gibt daher keinen Grund, es „herauszureißen“ bevor es
„hinzugefügt“ wird, wie in
YBC 6967 und
und
 .
Schließlich bestimmt der Text zuerst
.
Schließlich bestimmt der Text zuerst
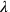 und
und
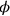 ,
und dann
,
und dann
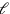 und
und
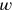 – wir erinnern daran, dass
– wir erinnern daran, dass
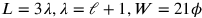 und
und
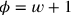 ist.
Weil 28 kein igi besitzt, erklärt Zeile 48, dass
ist.
Weil 28 kein igi besitzt, erklärt Zeile 48, dass
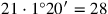 ist.
ist.
AO 8862 #2
I
(30)Länge, Breite. Länge und Breite
(31)habe ich enthalten lassen: Eine Fläche habe ich gebaut.
(32)Ich ging (um sie) herum. Die Hälfte der Länge
(33)und ein Drittel der Breite
(34)zum Innern der Fläche
(35)habe ich hinzugefügt: 15.
(36)Ich ging zurück. Länge und Breite
(37)habe ich angehäuft: 7.
II
(1)Länge und Breite was?
(2)Du, in deinem Verfahren,
(3)2 (als) Einschreibung der Hälfte
(4)und 3 (als) Einschreibung
(5)des Drittels schreibe ein:
(6)igi 2, 30′, spalte ab:
(7)30′ Schritte von 7, 3°30′; zu 7,
(8)den angehäuften Dingen, Länge und Breite,
(9)bringe ich:
(10)3°30′ von 15, meinen angehäuften Dingen.
(11)schneide ab:
(12)11°30′ der Rest.
(13)Geh nicht darüber hinaus. 2 und 3 lasse enthalten:
(14)3 Schritte von 2, 6.
(15)igi 6, 10′ gibt es Dir.
(16)10′ von 7, deinen angehäuften Dingen,
(17)Länge und Breite, reiße ich heraus:
(18)6°50′ der Rest.
(19)Sein Halbes, das von 6°50′, breche ich ab:
(20)3°25′ gibt es Dir.
(21)3°25′ zwei Mal
(22)schreibe ein; 3°25′ Schritte von 3°25′,
(23)11°40′25″; vom Innern
(24)11°30′ reiße ich heraus:
(25)10′25″ der Rest. ⟨Bei 10′25″, 25′ ist gleich ⟩.
(26)Zum ersten 3°25′
(27)25′ füge hinzu: 3°50′,
(28)und was von den angehäuften Dingen,
(29)Länge und Breite, ich herausgerissen habe,
(30)zu 3°50′ füge hinzu:
(31)4 die Länge. Von den zweiten 3°25′
(32)25′ reiße ich heraus: 3 die Breite.
32a.7 die angehäuften Dinge.
32b.4, die Länge; 3, die Breite; 12, die Fläche.
Die ersten beiden Wörter der ersten Zeile (I.30) sagen uns,
dass wir es mit einer Figur zu tun haben, die durch Länge
und Breite vollständig bestimmt ist, also mit einem Rechteck
(siehe Seite
Bevor wir das Verfahren untersuchen, wollen wir uns einige
Besonderheiten der Formulierung des Texts genauer ansehen. In
Zeile I.31 sehen wir, dass die Operation „enthalten lassen“
Der Text, ziemlich sicher aus Larsa, scheint um 1750 v.Chr. verfasst
worden zu sein und gehört daher zur frühen Phase der Übernahme der
Algebra durch die südlichen Schreiberschulen
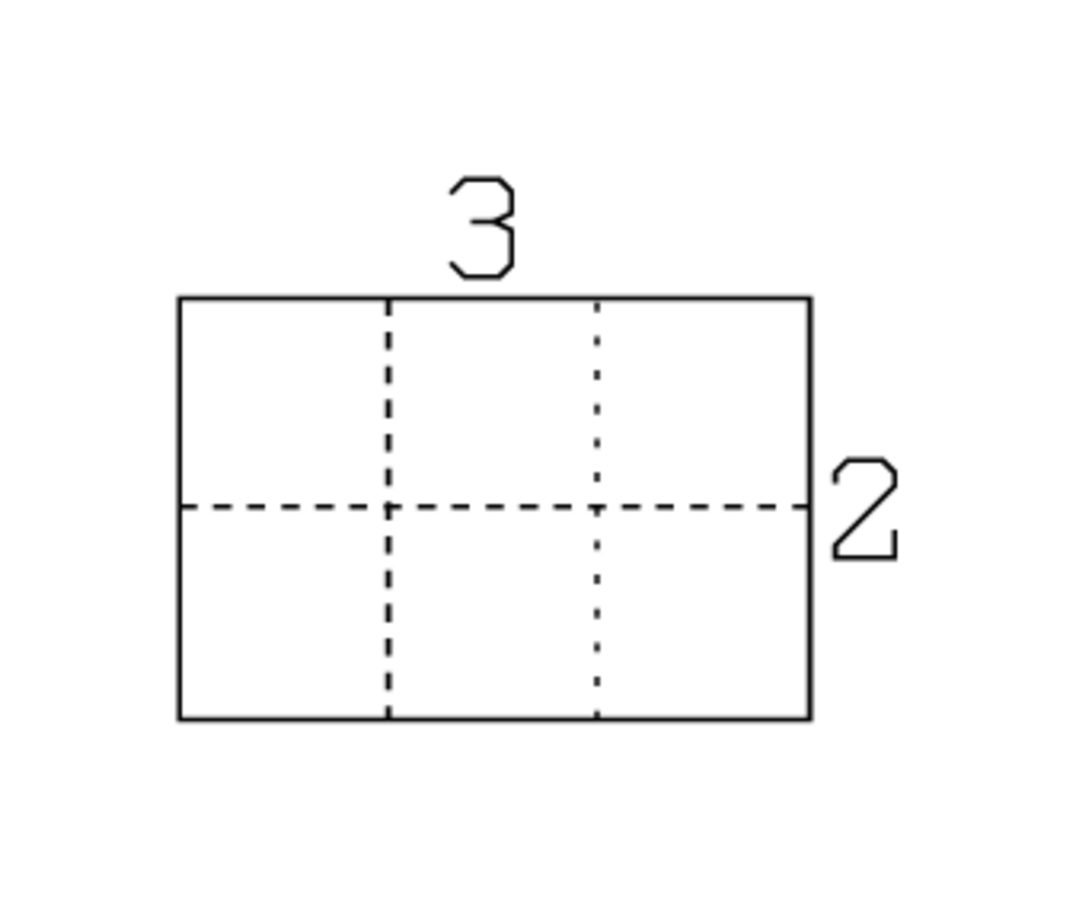
Das Thema der Aufgabe ist also ein Rechteck. Zeilen I.36–37 sagen uns, dass der „Haufen“ von Länge und Breite 7 ist, während die Zeilen I.32–35 sagen, dass das „Hinzufügen“ der halben Länge und eines Drittels der Breite zur „Fläche“ 15 ergibt:2
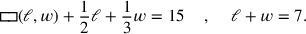
|
Der obere Teil von Abb. 4.2 illustriert diese Situation,
mit 2 und 3 „als Beschriftung“ von
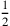 bzw.
bzw.
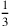 der „Projektionen“3 1
von Länge und Breite „eingeschrieben“ (Zeilen II.2–5); die dick gezeichnete Konfiguration hat
daher eine Fläche von 15.
der „Projektionen“3 1
von Länge und Breite „eingeschrieben“ (Zeilen II.2–5); die dick gezeichnete Konfiguration hat
daher eine Fläche von 15.
Die Lösung hätte dem Muster
TMS IX #3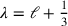 und einer „erweiterten Breite“
und einer „erweiterten Breite“
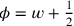 , und durch Addition (nach der
„akkadischen“ Methode)
, und durch Addition (nach der
„akkadischen“ Methode)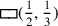 , das in der Ecke fehlt,
in der 2 und 3 „eingeschrieben“ sind, hätten wir das
Problem auf
, das in der Ecke fehlt,
in der 2 und 3 „eingeschrieben“ sind, hätten wir das
Problem auf
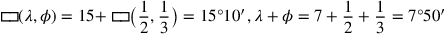
|
reduziert.
Der vorliegende Text geht jedoch nicht so vor –
die altbabylonische Algebra war ein flexibles Instrument,
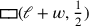 (repräsentiert durch
die Zahl 3°30′) wird physisch an den Platz
gebracht, an dem sich Länge und Breite (welche die Breiten
(repräsentiert durch
die Zahl 3°30′) wird physisch an den Platz
gebracht, an dem sich Länge und Breite (welche die Breiten
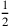 und
und
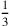 besitzen) befinden.
Dadurch wird es möglich, das Rechteck
besitzen) befinden.
Dadurch wird es möglich, das Rechteck
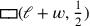 „abzuschneiden“ – solange es anderswo war, hätte dies
keinen Sinn gehabt. In Abb. 4.2 ist die Fläche,
die eliminiert wird, schattiert und schwarz gezeichnet: der Rest,
in weiß, ist dann gleich 11°30′.
„abzuschneiden“ – solange es anderswo war, hätte dies
keinen Sinn gehabt. In Abb. 4.2 ist die Fläche,
die eliminiert wird, schattiert und schwarz gezeichnet: der Rest,
in weiß, ist dann gleich 11°30′.
Wir wissen also, dass wir, zusätzlich zu dem Drittel der Breite, ein Rechteck
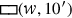 (schwarz gezeichnet) eliminiert haben;
mit
(schwarz gezeichnet) eliminiert haben;
mit
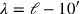 haben wir also
haben wir also
|
Einmal mehr haben wir also ein Rechteck, von dem wir die
Fläche und die Summe von Länge und Breite kennen. Das Verfahren ist
dasselbe wie am Ende von TMS IX #3
Am Schluss geht die Addition der Seite des Quadrats der Subtraktion voraus, ebenso wie in TMS IX #3. Einmal mehr wird bei diesen Operationen nicht dasselbe Stück verwendet; es gibt daher keinen Grund, es zur Verfügung zu stellen, bevor es addiert wird.
VAT 7532
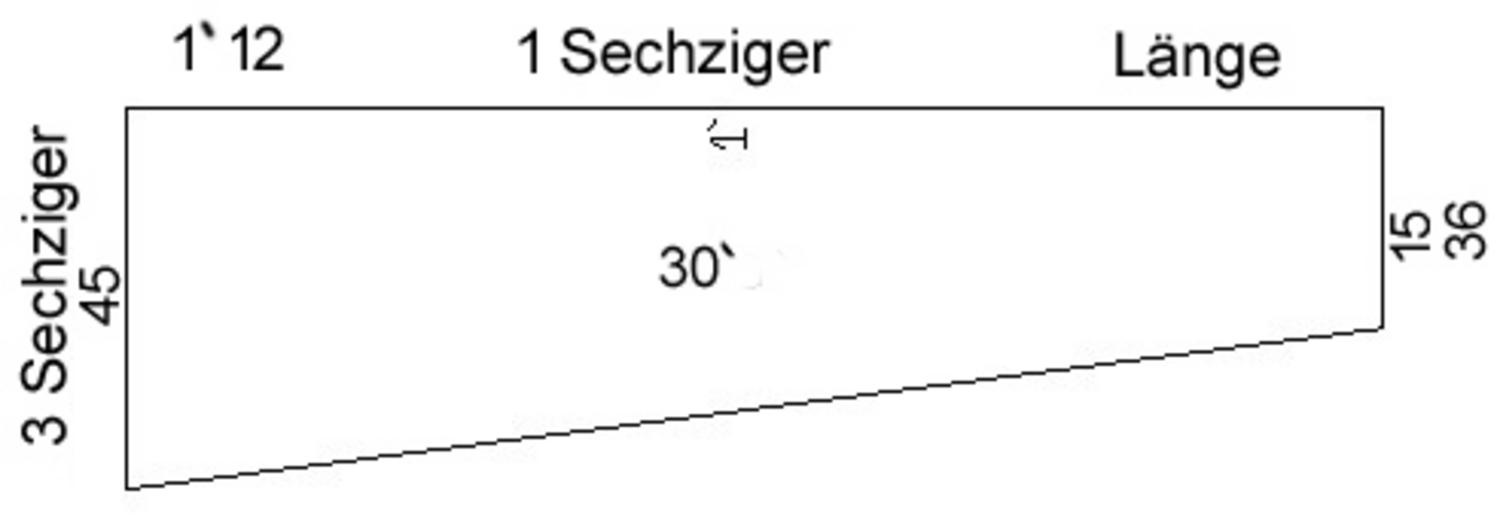
Abb. 4.5: Das Diagramm von VAT 7532. Die „obere Breite“ ist links zu sehen.
Vs.
(1)Ein Trapez. Ich habe ein Schilfrohr
geschnitten.
(2)1 Sechzig längs der Länge bin ich gegangen. Der 6te Teil
(3)ist mir abgebrochen: 1‵12 entlang der Länge bin ich weitergegangen.
(4)Ich bin umgekehrt. Der 3te Teil und
 kùš
sind mir abgebrochen:
kùš
sind mir abgebrochen:
(5)3 Sechzig entlang der oberen Breite bin ich gegangen.
(6)Mit dem Abgebrochenen habe ich es verlängert:
(7)36 bin ich entlang der Breite gegangen. 1 bùr
(8)Du, bei Deinem Verfahren, (für) das Schilfrohr, das Du nicht kennst,
(9)1 mögest Du setzen. Dessen 6ten Teil brich ab, 50′ lässt Du zurück.
(10)igi 50′ spalte ab, 1°12′ auf 1 Sechzig erhöhe:
(11)1‵12 zu ⟨1‵12⟩ füge hinzu: 2‵24 die falsche Länge gibt es Dir.
(12)Für das Schilfrohr, das Du nicht kennst, 1 setze. Dessen 3ten Teil brich ab,
(13)40′ auf 3 Sechziger der oberen Breite erhöhe:
(14)2‵ gibt es Dir. 2‵ und 36, die untere Breite, häufe an,
(15)2‵36 auf 2‵24, die falsche Länge, erhöhe, 6‶14‵24 die falsche Fläche.
(16)Die Fläche bis 2 wiederhole, 1‶ auf 6‶14‵24 erhöhe,
(17)6‶‶14‷24‶ ergibt es.
Und
 kùš, was abgebrochen ist,
kùš, was abgebrochen ist,
(18)auf 3 Sechziger erhöhe: 5 auf 2‵24, die falsche Länge,
(19)erhöhe: 12‵.
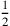 von 12‵ brich ab,
6‵ lass enthalten,
von 12‵ brich ab,
6‵ lass enthalten,
Rs.
(1)36‶ zu 6‶‶14‷24‶ füge hinzu, 6‶‶15‷ ergibt es.
(2)Bei 6‶‶15‷, 2‶30′ ist gleich. 6‵ welche du zurückgelassen hast,
(3)zu 2‶30‵ füge hinzu, 2‶36‵ ergibt es. igi 6‶14‵24,
(4)die falsche Fläche, kenne ich nicht. Was muss ich zu 6‶14‵24
(5)setzen, das mir 2‶36 gibt? 25′ setze.
(6)Weil der 6te Teil zuvor abgebrochen ist,
(7)6 schreibe ein: 1 lass weggehen
(8)⟨igi 5 spalte ab, 12′ zu 25 erhöhe,
5′ gibt es Dir ⟩.
5′ zu 25′ füge hinzu:
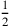 nindan, den Kopf des Schilfrohrs gibt es Dir.
nindan, den Kopf des Schilfrohrs gibt es Dir.
Dieses Problem handelt ebenfalls von einer Fläche – allerdings einer
Fläche, welche einem Feldmesser nur im Traum begegnet (genauer in einem
Alptraum). Das „wirkliche Leben“ kommt durch den Bezug
auf die Einheit bùr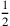 nindan)
entspricht in der Tat einer Maßeinheit, die im täglichen Leben oft verwendet
wurde, und die genau als „Schilfrohr“ bezeichnet wurde (gi
auf Sumerisch). Man darf davon ausgehen, dass solche Schilfrohre leicht brechen.
Schließlich zeigt uns der Gebrauch des Zahlworts „sechzig“ eine
Möglichkeit, Zahlen eindeutig auszudrücken.
nindan)
entspricht in der Tat einer Maßeinheit, die im täglichen Leben oft verwendet
wurde, und die genau als „Schilfrohr“ bezeichnet wurde (gi
auf Sumerisch). Man darf davon ausgehen, dass solche Schilfrohre leicht brechen.
Schließlich zeigt uns der Gebrauch des Zahlworts „sechzig“ eine
Möglichkeit, Zahlen eindeutig auszudrücken.
Alles andere jedoch – dass also die Fläche des Feldes bekannt ist, bevor
sie gemessen wird, und auch die Art, die Maße der vom Schilfrohr abgebrochen
Stücke anzugeben – zeigt, zu welchen Mitteln die altbabylonischen Schulmeister
greifen mussten, um Probleme zweiten
Grades
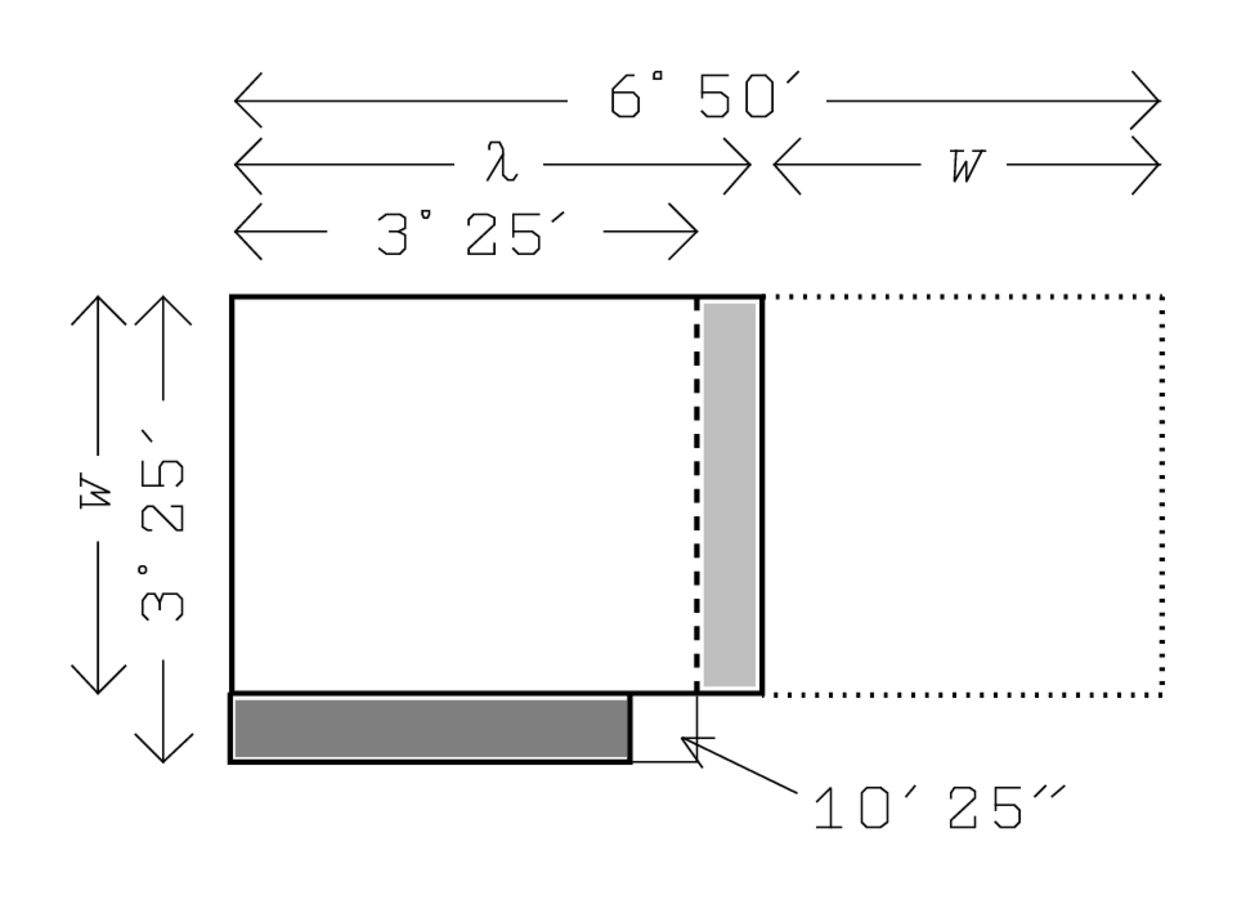
Abbildung 4.5 zeigt ein Diagramm, das ausnahmsweise auf der
Tafel selbst zu finden ist. Im allgemeinen, wie auch hier, werden Diagramme
nur auf Tafeln gezeichnet, wenn sie dazu dienen, die Aussage zu präzisieren;
sie werden nie genutzt um das Verfahren zu erklären. Zum Anderen zeigt
Abbildung 4.5 einmal mehr, dass die Lösung im Voraus bekannt ist:
Die Zahlen 1‵, 45 und 15 sind in der Tat die Maße der Seiten,
ausgedrückt in nindan.
Wir messen also das Trapez mittels eines Schilfrohrs unbekannter Länge
 .
Wir schaffen es, 1‵ Schilfrohrlängen entlang der Länge des
Trapezes zu messen, bevor das Schilfrohr ein Sechstel seiner Länge verliert
und auf
.
Wir schaffen es, 1‵ Schilfrohrlängen entlang der Länge des
Trapezes zu messen, bevor das Schilfrohr ein Sechstel seiner Länge verliert
und auf
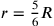 reduziert wird. Was von der Länge bleibt,
stellt sich als 1‵12
reduziert wird. Was von der Länge bleibt,
stellt sich als 1‵12
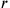 heraus (Zeilen Vs. 2-3).
heraus (Zeilen Vs. 2-3).
Dann bricht das Schilfrohr zum zweiten Mal. Nach den Zeilen Vs. 4 und 5
ist das Maß für die „obere Breite“ (auf der linken
Seite)5
gleich 3‵
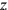 , wobei
, wobei
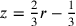 kùš
die Länge des Schilfrohrs nach dieser zweiten Reduktion ist.
kùš
die Länge des Schilfrohrs nach dieser zweiten Reduktion ist.
Das Stück, das zuletzt abgebrochen ist, wird wieder an seinen Platz
gesetzt, und die „(untere) Breite“ (offensichtlich diejenige
auf der rechten Seite) wird als 36 r abgeschritten (Zeile Vs. 7).
Schließlich erfahren wir, dass die Fläche des Feldes
1 bùr = 30‵ sar
(1 sar = 1 nindan2, siehe Seite
Die Zeilen Vs. 9-11 bestimmen die Länge in der Einheit
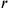 durch einen falschen Ansatz: wenn
durch einen falschen Ansatz: wenn
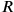 gleich 1 gewesen wäre,
dann wäre
gleich 1 gewesen wäre,
dann wäre
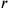 gleich 50′;
gleich 50′;
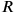 muss umgekehrt
muss umgekehrt
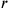 multipliziert mit igi
multipliziert mit igi
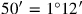 entsprechen. 1‵ Schritte von
entsprechen. 1‵ Schritte von
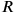 entsprechen somit
entsprechen somit
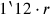 , und die Gesamtlänge wird
, und die Gesamtlänge wird
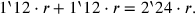
|
Der Text spricht von 2‵24 als der
„falschen Länge“, also der Länge, welche in der
Einheit Einheit
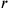 ausgedrückt wird.
ausgedrückt wird.
Ein weiterer falscher Ansatz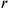 des einmal gekürzten
Schilfrohrs und folgert, dass das, was nach dem
Verlust von
des einmal gekürzten
Schilfrohrs und folgert, dass das, was nach dem
Verlust von
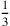
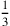 kùš ab,
ist die falsche obere Breite (die obere Breite gemessen in der
Einheit
kùš ab,
ist die falsche obere Breite (die obere Breite gemessen in der
Einheit
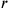 ) demnach 40′ multipliziert mit
3 Sechzigern, also
) demnach 40′ multipliziert mit
3 Sechzigern, also
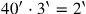 . Mit anderen Worten, die
obere Breite misst 2‵
. Mit anderen Worten, die
obere Breite misst 2‵
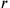 – immer noch unter Vernachlässigung
des fehlenden Stücks von
– immer noch unter Vernachlässigung
des fehlenden Stücks von
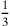 kùš.
kùš.
Weil Zeile Vs. 7 anzeigt, dass die falsche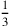 kùš – die drei Seiten, was
uns die Bestimmung der Fläche des Trapezes in der Einheit
kùš – die drei Seiten, was
uns die Bestimmung der Fläche des Trapezes in der Einheit
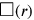 erlaubt.
erlaubt.
Der Text berechnet diese Fläche jedoch nicht: Die Fläche
bis 2 wiederhole. Stattdessen verdoppelt er das Trapez, sodass ein
Rechteck entsteht (siehe den linken Teil von Abbildung 4.6),
und die Zeilen Vs. 14-16 berechnen die Fläche dieses Rechtecks
(die „falsche Fläche“)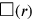 ).
).
Wenn das Schilf nicht ein letztes Stück von
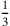 kùš verloren hätte, könnten wir jetzt
die Lösung durch einen letzten falschen Ansatz ähnlich demjenigen von
BM 13901 #10
kùš verloren hätte, könnten wir jetzt
die Lösung durch einen letzten falschen Ansatz ähnlich demjenigen von
BM 13901 #10 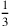 kùš
in unserer Rechnung; das macht insgesamt also
kùš
in unserer Rechnung; das macht insgesamt also
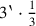 kùš = 1‵ kùš
= 5 nindan (1 kùš =
kùš = 1‵ kùš
= 5 nindan (1 kùš =
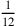 nindan):
Und
nindan):
Und
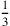 kùš, welches abgebrochen ist,
auf 3 Sechziger erhöhe: 5 (Vs. 17–18). Daher entspricht die Fläche des echten
Feldes nicht dem, was wir links in Abbildung 4.6 sehen, sondern dem,
was nach der Abspaltung des schattierten Streifens auf der rechten Seite übrig
bleibt. Die Fläche dieses Streifens ist
kùš, welches abgebrochen ist,
auf 3 Sechziger erhöhe: 5 (Vs. 17–18). Daher entspricht die Fläche des echten
Feldes nicht dem, was wir links in Abbildung 4.6 sehen, sondern dem,
was nach der Abspaltung des schattierten Streifens auf der rechten Seite übrig
bleibt. Die Fläche dieses Streifens ist
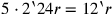 :
5 auf 2‵24, die falsche Länge, erhöhe: 12‵.
Die Beziehung zwischen der „falschen Fläche“
:
5 auf 2‵24, die falsche Länge, erhöhe: 12‵.
Die Beziehung zwischen der „falschen Fläche“
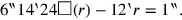
|
Diese nicht-normierte Gleichung wird auf die übliche Weise gelöst. Zuerst wird sie multipliziert mit 6‶14‵24: 1‶ auf 6‶14‵24 erhöhe: 6‶‶14‷24‶ ergibt es (Vs. 16–17). Dies führt zur normalisierten Gleichung
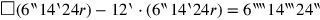
|
oder, mit
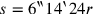 r als Unbekannter,
r als Unbekannter,
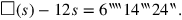
|
Ab hier stimmt das Verfahren mit dem von
BM 13901 #2
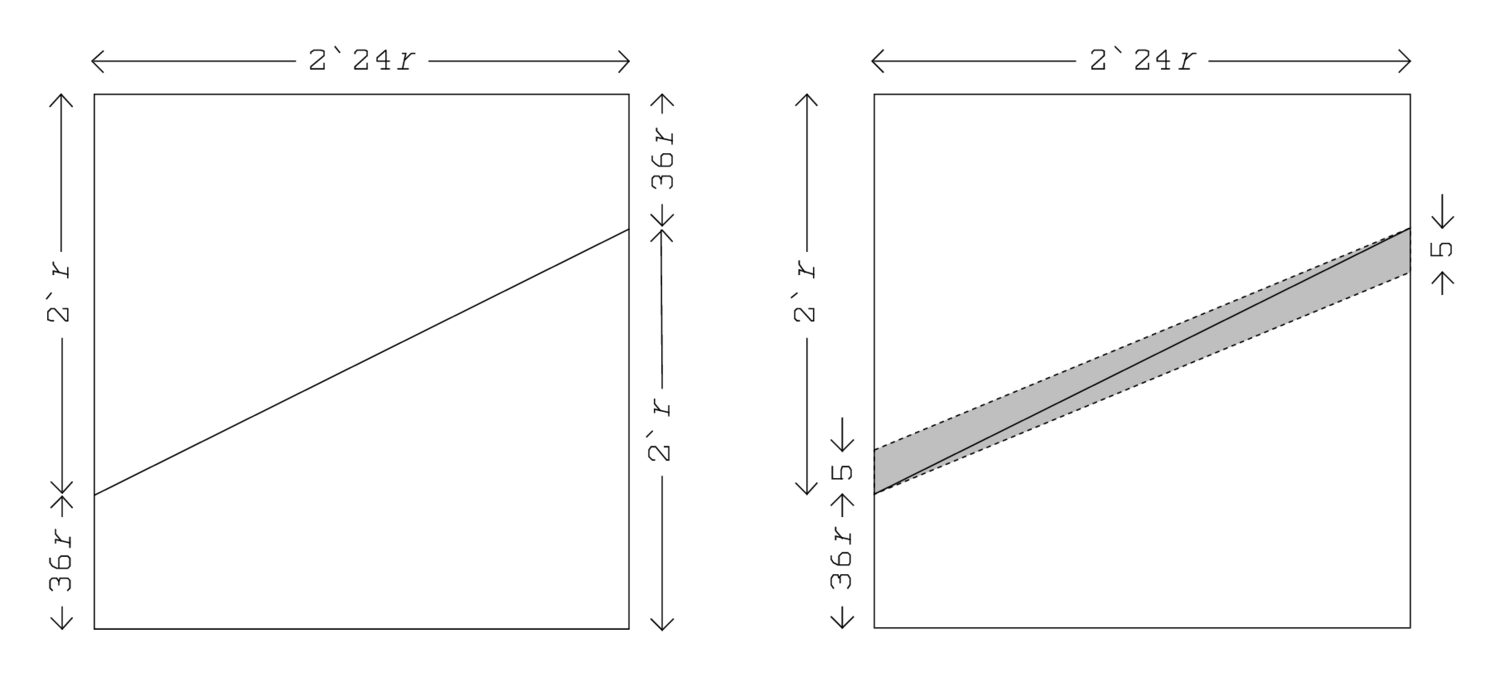
Die Fläche 6‶‶14‷24‶ entspricht dem Rechteck mit
(der Höhe)
 und der Breite
und der Breite
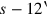 . Die Hälfte des
Überschusses der Höhe über die Breite wird „abgebrochen“ und,
wie im Diagramm zu sehen, neu positioniert: die ursprüngliche Position ist
leicht, die neue stark schattiert. Die Konstruktion der quadratischen Ergänzung
wird mit einem der Synonyme
. Die Hälfte des
Überschusses der Höhe über die Breite wird „abgebrochen“ und,
wie im Diagramm zu sehen, neu positioniert: die ursprüngliche Position ist
leicht, die neue stark schattiert. Die Konstruktion der quadratischen Ergänzung
wird mit einem der Synonyme
Nach den üblichen Operationen finden wir
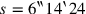
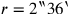 ,
und in Zeile Rs. 5
,
und in Zeile Rs. 5
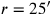 . Wir stellen jedoch fest, dass das
„Halbe“, das herumbewegt worden ist, nicht wieder in seine
ursprüngliche Lage zurückgesetzt wird, was s in der vertikalen
Richtung wieder hergestellt hätte. Stattdessen wird das andere „Halbe“,
die ursprünglich an ihrem Platz gelassen wurde, jetzt ebenfalls bewegt,
was eine horizontale Wiederherstellung von
. Wir stellen jedoch fest, dass das
„Halbe“, das herumbewegt worden ist, nicht wieder in seine
ursprüngliche Lage zurückgesetzt wird, was s in der vertikalen
Richtung wieder hergestellt hätte. Stattdessen wird das andere „Halbe“,
die ursprünglich an ihrem Platz gelassen wurde, jetzt ebenfalls bewegt,
was eine horizontale Wiederherstellung von
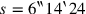
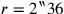 erlaubt: 6‵,
was du liegen lassen hast, zu 2‶30‵ füge hinzu,
2‶36‵ ergibt es.6
erlaubt: 6‵,
was du liegen lassen hast, zu 2‶30‵ füge hinzu,
2‶36‵ ergibt es.6
In den Zeilen Rs. 6–8 führt der Rechner einen dritten
falschen Ansatz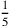 von r oder 12′ mal r. Jetzt folgt der wahre Wert
r zu 25′; um R zu erhalten müssen wir also
von r oder 12′ mal r. Jetzt folgt der wahre Wert
r zu 25′; um R zu erhalten müssen wir also
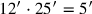 dazu „hinzufügen“. Folglich
ist
dazu „hinzufügen“. Folglich
ist
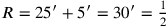 nindan.
nindan.
Man könnte glauben, dass dieser Problemtyp
zu den absoluten Favoriten der
altbabylonischen Lehrer für anspruchsvolle Mathematik zählt.
Wir kennen vier Varianten, die sich in der Wahl der numerischen
Parameter unterscheiden. Sie alle gehören jedoch zu nur zwei Tafeln,
die eine Reihe von terminologischen Besonderheiten gemeinsam haben –
zum Beispiel, die Verwendung des Logogramms
 für das „Halbe“, und die Angewohnheit, dass die Ergebnisse
„gegeben“ sind, und nicht etwa „gesehen“ werden
oder „aufkommen“. Sicherlich sind beide Tafeln Produkte aus
der gleichen Gegend und derselben lokalen Tradition (der Rechtschreibung
nach aus der Gegend von Uruk), und sie kommen wahrscheinlich aus der gleichen
Schule oder sind sogar von der gleichen Hand geschrieben worden.
Eine einfachere Variante mit einem rechteckigen Feld findet sich jedoch in einem
früheren Text aus dem Norden und auch in einem Text, welcher mit der Variante mit
dem Trapez zusammengehört. Wenn das abgebrochene Schilfrohr nicht das
Lieblingsproblem ist, dann doch eines.
für das „Halbe“, und die Angewohnheit, dass die Ergebnisse
„gegeben“ sind, und nicht etwa „gesehen“ werden
oder „aufkommen“. Sicherlich sind beide Tafeln Produkte aus
der gleichen Gegend und derselben lokalen Tradition (der Rechtschreibung
nach aus der Gegend von Uruk), und sie kommen wahrscheinlich aus der gleichen
Schule oder sind sogar von der gleichen Hand geschrieben worden.
Eine einfachere Variante mit einem rechteckigen Feld findet sich jedoch in einem
früheren Text aus dem Norden und auch in einem Text, welcher mit der Variante mit
dem Trapez zusammengehört. Wenn das abgebrochene Schilfrohr nicht das
Lieblingsproblem ist, dann doch eines.
TMS XIII
Wie TMS VII #2
(1)2 gur 2 pi 5 bán Öl habe ich gekauft. Von was ich für 1 Schekel Silber gekauft habe,
(2)4 silà jedes (Schekel) Öl habe ich weggenommen.
(3)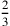 Minen Silber Profit habe ich gesehen. Entsprechend wozu
Minen Silber Profit habe ich gesehen. Entsprechend wozu
(4)habe ich gekauft und entsprechend wozu habe ich verkauft?
(5)Du 4 silà Öl setze und 40, (von der Größenordnung der) Mine, als Profit setze.
(6)igi 40 spalte ab, 1′30″ siehst Du, 1′30″ auf 4 erhöhe, 6′ siehst Du.
(7)6′ auf 12‵50, das Öl, erhöhe, 1‵17 siehst Du.
(8)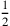 von 4 brich ab, 2 siehst Du, 2 lasse enthalten, 4 siehst Du.
von 4 brich ab, 2 siehst Du, 2 lasse enthalten, 4 siehst Du.
(9)4 zu 1‵17 füge hinzu, 1‵21 siehst Du. Wobei ist es gleich? 9 ist gleich.
(10)9 die Gegenseite setze.
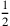 von 4, was du weggenommen hast,
brich ab, 2 siehst Du.
von 4, was du weggenommen hast,
brich ab, 2 siehst Du.
(11)2 zu der ersten 9 füge hinzu, 11 siehst Du; von der zweiten reiße es ab,
(12)7 siehst Du. 11 silà jedes (Schekel) hast Du gekauft, 7 silà hast Du verkauft.
(13)Silber entspricht was? Was zu 11 ¿silà? kann ich setzen
(14)was 12‵50 Öl ergibt? 1‵10 setze, 1 Mine 10 Schekel Silber.
(15)Durch 7 silà jedes (Schekel) was du an Öl verkauft hast,
(16)das von 40 Silber entspricht was? 40 auf 7 erhöhe,
(17)4‵40 siehst Du, 4‵40 Öl.
Das ist ein weiteres Problem,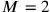 gur 2 pi 5 bán
(= 12‵50 sìla) feines Öl (wahrscheinlich Sesamöl) gekauft.
Uns wird nicht gesagt, wie viel er zahlte, aber der Text informiert uns, dass er
von dem Öl, das er für einen Schekel (a) gekauft hat, 4 sìla abgezogen
hat: Was er für einen Schekel gekauft hat, können wir a nennen. Dann verkauft er
für einen Schekel
gur 2 pi 5 bán
(= 12‵50 sìla) feines Öl (wahrscheinlich Sesamöl) gekauft.
Uns wird nicht gesagt, wie viel er zahlte, aber der Text informiert uns, dass er
von dem Öl, das er für einen Schekel (a) gekauft hat, 4 sìla abgezogen
hat: Was er für einen Schekel gekauft hat, können wir a nennen. Dann verkauft er
für einen Schekel
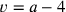 (beide in Einheiten sìla). Dabei hat er
einen Gewinn von
(beide in Einheiten sìla). Dabei hat er
einen Gewinn von
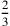 mina = 40 Schekel Silber gemacht.
Hier sind
mina = 40 Schekel Silber gemacht.
Hier sind
 und
und
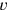 die Reziproken der beiden Preise – wir dürfen
von ihnen als „Raten“ des Kaufs und Verkaufs sprechen.
Für uns, die wir mit algebraischer Symbolik vertraut sind, ist es leicht zu
erkennen, dass der Gesamtkaufpreis (die Investition)
die Reziproken der beiden Preise – wir dürfen
von ihnen als „Raten“ des Kaufs und Verkaufs sprechen.
Für uns, die wir mit algebraischer Symbolik vertraut sind, ist es leicht zu
erkennen, dass der Gesamtkaufpreis (die Investition)
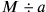 , der
Gesamtverkaufspreis
, der
Gesamtverkaufspreis
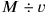 , und der Gewinn folglich
, und der Gewinn folglich
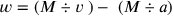 sein muss. Multipliziert man mit
sein muss. Multipliziert man mit
 , so erhält man die Gleichung
, so erhält man die Gleichung
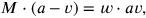
|
und wegen
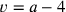 das System
das System
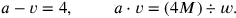
|
Diese System, das vom selben Typ ist wie das igûm-igibûm
Problem (Seite 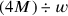 gefunden und eben nicht
gefunden und eben nicht
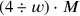 .
.
Der Hinweis auf ihre Methode taucht gegen Ende des Textes auf. Hier findet der Text zuerst die Gesamtinvestition und als nächstes den Gewinn in Öl (4‵40 sìla). Diese Berechnungen stellen keinen Beweis dar, da diese Größen nicht gegeben waren. Nach ihnen ist aber auch nicht gefragt. Sie müssen interessant sein, weil sie bei der Suche nach der Lösung eine Rolle gespielt haben.
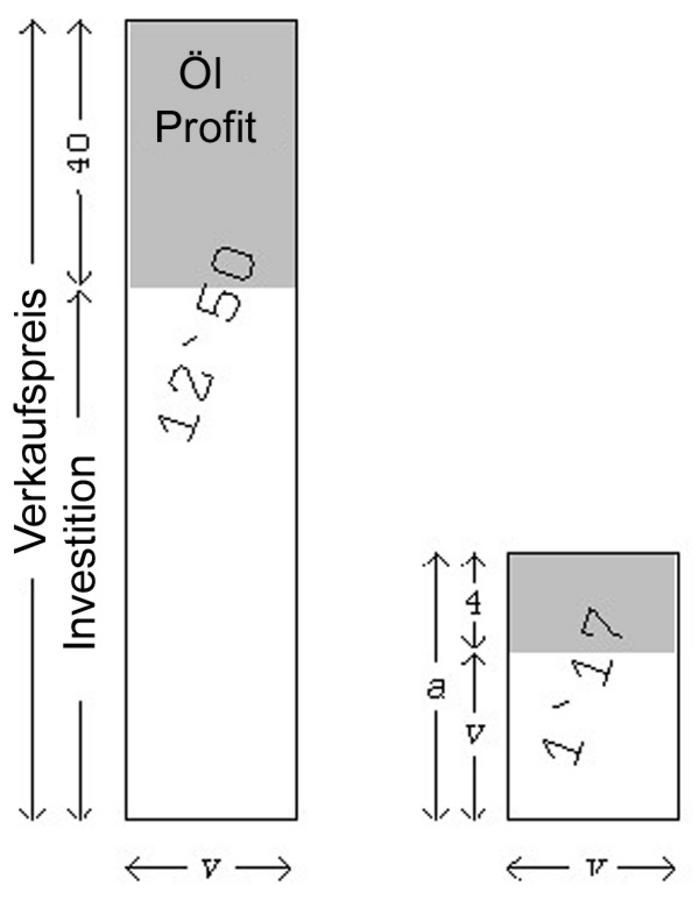
Abbildung 4.8 zeigt eine mögliche und im Prinzip
plausible Interpretation. Die Gesamtmenge des Öls wird durch ein
Rechteck dargestellt, dessen Höhe dem Gesamtverkaufspreis in Schekel
und dessen Breite der „Verkaufsrate“
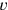 (sìla pro Schekel) entspricht.
Der gesamte Verkaufspreis kann in den Gewinn (40 Schekel) und
die Investition (Kaufpreis) eingeteilt werden, und die Ölmenge in ähnlicher
Weise in den Ölgewinn und in die Menge, deren Verkauf die Investition zurückbringt.
(sìla pro Schekel) entspricht.
Der gesamte Verkaufspreis kann in den Gewinn (40 Schekel) und
die Investition (Kaufpreis) eingeteilt werden, und die Ölmenge in ähnlicher
Weise in den Ölgewinn und in die Menge, deren Verkauf die Investition zurückbringt.
Das Verhältnis zwischen den beiden letzten Größen muss mit dem Verhältnis
übereinstimmen, in das die für einen Schekel gekaufte Menge geteilt wurde,
also mit dem Verhältnis zwischen 4 sìla und dem, was für 1 Schekel
verkauft wird (also
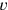 ).
).
Ändert man den vertikalen Maßstab 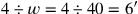 , dann wird die Investition
auf
, dann wird die Investition
auf
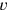 verringert, und die Fläche auf
verringert, und die Fläche auf
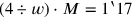 .
Auf diese Weise erhalten wir das Rechteck auf der rechten Seite, von dem wir die
Fläche (
.
Auf diese Weise erhalten wir das Rechteck auf der rechten Seite, von dem wir die
Fläche (
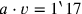 ) und die Differenz zwischen den Seiten
(
) und die Differenz zwischen den Seiten
(
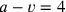 ) kennen, genau so, wie es sein soll. Außerdem folgen wir dem
Text in der Reihenfolge der Operationen, und der Profit beim Ölverkauf sowie die
Investition spielen eine Rolle.
) kennen, genau so, wie es sein soll. Außerdem folgen wir dem
Text in der Reihenfolge der Operationen, und der Profit beim Ölverkauf sowie die
Investition spielen eine Rolle.
Insgesamt folgt der letzte Teil des Verfahrens dem Modell von
YBC 6967 zu benutzen, das wir in Zeile 8 „enthalten lassen“
haben, wird
zu benutzen, das wir in Zeile 8 „enthalten lassen“
haben, wird
 ein zweites Mal „gebrochen“. Dies erlaubt
uns zuerst das „Hinzufügen“
ein zweites Mal „gebrochen“. Dies erlaubt
uns zuerst das „Hinzufügen“
Bei der igûm-igibûm-Aufgabe auf YBC 6967 (Seite
BM 13901 #12
Vs. II
(27)Die Flächen meiner beiden Gegenseiten habe ich angehäuft: 21′40″.
(28)Meine Gegenseiten habe ich enthalten lassen: 10′.
(29)Das Halbe meiner 21′40″ brichst Du: 10′50″ und 10′50″ lässt Du enthalten,
(30)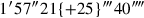 7 ist es.
10′ und 10′ machst Du
enthalten, 1′40″
7 ist es.
10′ und 10′ machst Du
enthalten, 1′40″
(31)aus
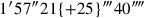 reißt Du heraus: bei
reißt Du heraus: bei
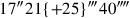 ,
4′10″ ist gleich.
,
4′10″ ist gleich.
(32)4′10″ zum einen 10′50″ fügst Du hinzu: bei 15′, 30′ ist gleich.
(33)30′ die erste Gegenseite.
(34)4′10″ aus dem zweiten 10′50″ reißt Du heraus: bei 6′40″, 20′ ist gleich.
(35)20′ die zweite Gegenseite.
Mit diesem Problem verlassen wir den Bereich der pseudo-praktischen Aufgaben und kehren zur Geometrie abgemessener geometrischer Größen zurück. Bei dem Problem, das wir betrachten werden, werden wir auf einen möglicherweise noch bemerkenswerteren Fall von Darstellung treffen.
Dieses Problem stammt aus der Aufgabensammlung und
und
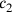 „enthalten“ (siehe Abb. 4.9):
„enthalten“ (siehe Abb. 4.9):
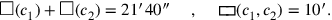
|
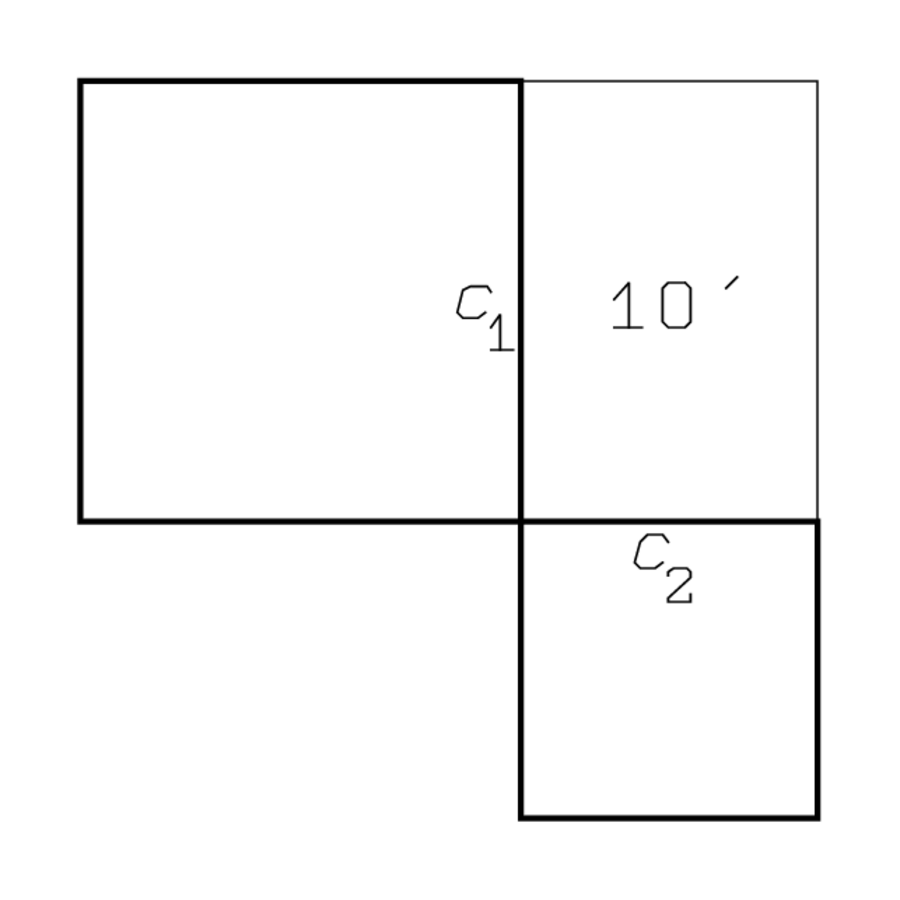
Abb. 4.9: Die beiden Quadrate und das Rechteck von BM 13901 #12.
Dies Aufgabe hätte mit den Methoden der Figur in Abb. 4.10
gelöst werden können, das anscheinend bereits für die Lösung des Problems
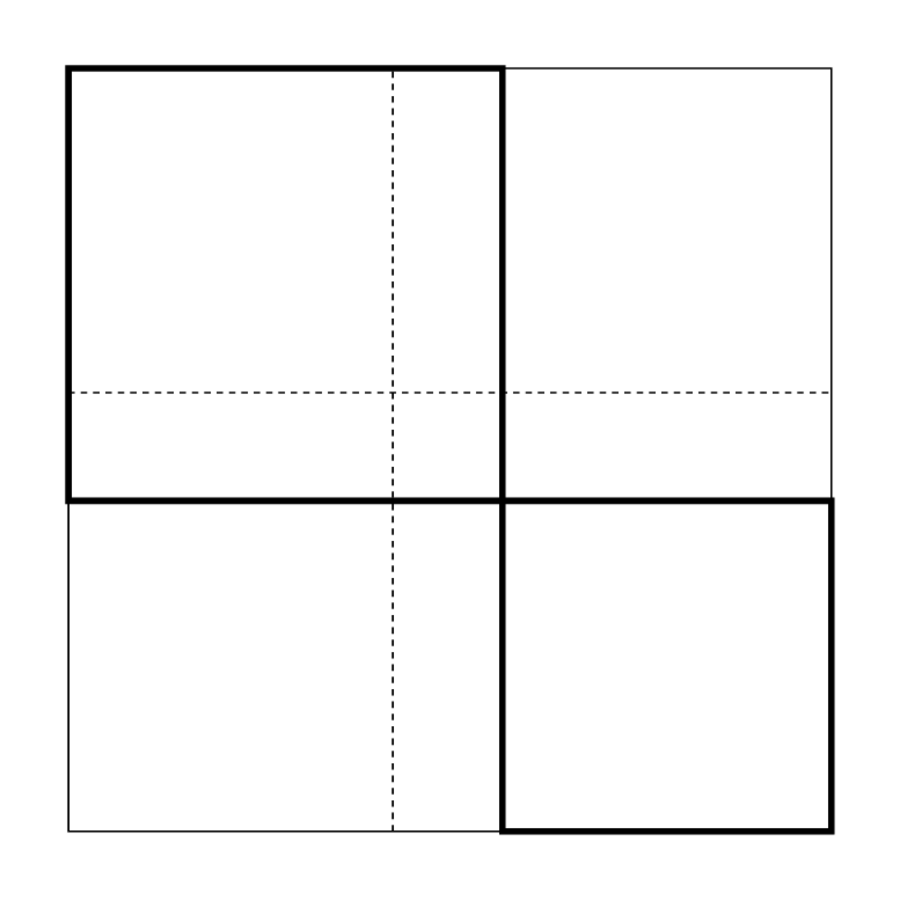
Abb. 4.10: Das Diagramm zur Lösung von BM 13901 #8.
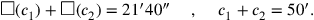
|
Der Autor wählt jedoch eine andere Methode und unterstreicht so die Flexibilität der
algebraischen Technik. Er nimmt die beiden Flächen
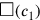 und
und
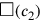 als die Seiten
eines Rechtecks, dessen Fläche er findet, indem er 10′ und
10′ „enthalten lässt“ (siehe Abb. 4.10):
als die Seiten
eines Rechtecks, dessen Fläche er findet, indem er 10′ und
10′ „enthalten lässt“ (siehe Abb. 4.10):
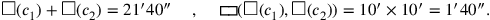
|
Trotz des geometrischen Charakters der Operationen war es
den Babyloniern durchaus bewusst, dass die Fläche eines Rechtecks,
dessen Seiten die Quadrate
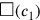 und
und
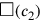 sind, mit dem eines Quadrats zusammenfällt, dessen Seite das Rechteck
sind, mit dem eines Quadrats zusammenfällt, dessen Seite das Rechteck
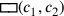 ist – dies entspricht unserer algebraischen Regel
ist – dies entspricht unserer algebraischen Regel
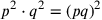 .
.
Jetzt haben wir ein Rechteck, für das wir die Fläche und die Summe
der beiden Seiten kennen, wie in den Aufgaben
TMS IX #3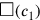 und
und
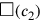 geben. Zur Berechnung von
geben. Zur Berechnung von
 und
und
 müssen wir noch herausfinden,
„wobei sie gleich“ sind. Die Rechnungen kann man
in Abb. 4.11 verfolgen.
müssen wir noch herausfinden,
„wobei sie gleich“ sind. Die Rechnungen kann man
in Abb. 4.11 verfolgen.
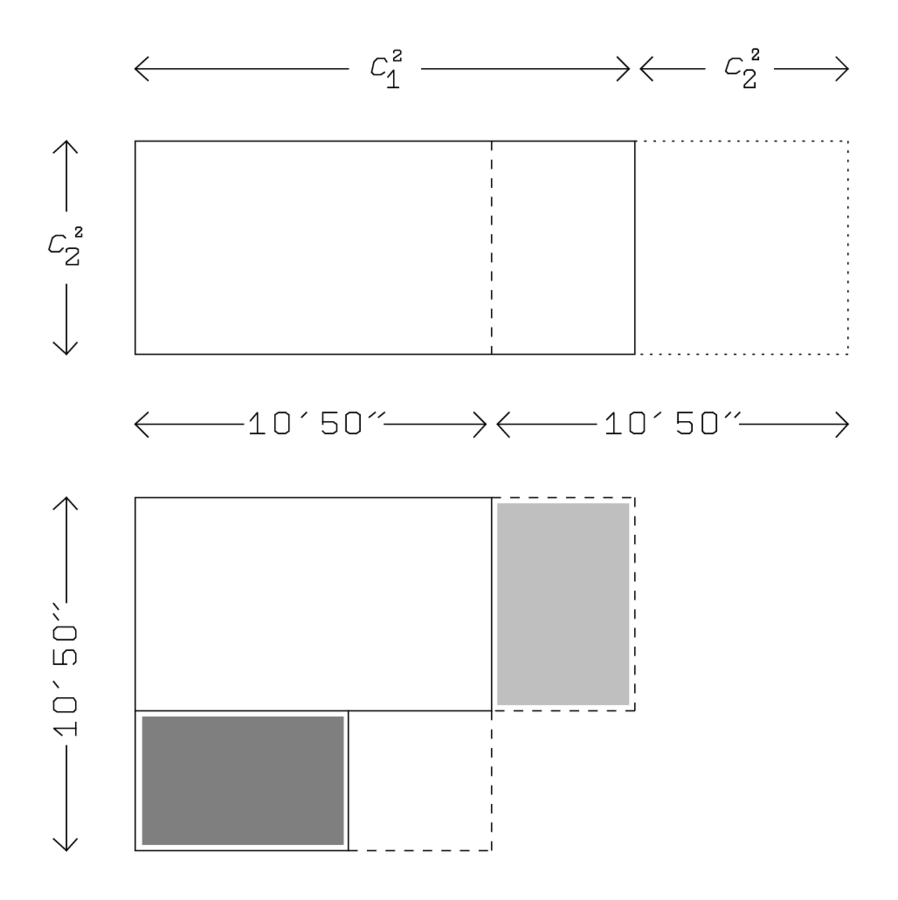
Abb. 4.11: Die bei der Lösung des Rechteckproblems benutzte Prozedur.
Bei diesem Problem ist die Tatsache beachtenswert, dass hier
Flächen durch Strecken und und das Quadrat der Fläche
durch eine Fläche dargestellt wird.
BM 13901 #23
Rs. II
(11)Über eine Fläche; die vier Breiten und die Fläche habe ich angehäuft, 41′40″.
(12)4, die vier Breiten, schreibe ein. igi 4 ist 15′.
(13)15′ auf 41′40″ erhöhe: 10′25″ schreibe ein.
(14)1, die Projektion, füge hinzu: bei 1°10′25″, 1°5′ ist gleich.
(15)1, die Projektion, welche Du hinzugefügt hast, reiße heraus: 5′ bis zwei
(16)wiederhole: 10′, nindan, steht sich gegenüber.
Während das vorherige Problem den „modernen“ Aspekt der altbabylonischen Mathematik unterstreicht, scheint dieses hier die archaische Seite zu betonen – obwohl sie beide von derselben Tafel stammen.
Dies ist kein wirklicher Widerspruch. Das vorliegende Problem
Die einführende Phrase „Über eine Fläche“8 scheint eine Abkürzung der
charakteristischen Formel zu sein, die mathematische Rätsel einleitet:
„Wenn Dich jemand über eine Fläche fragt ...“ (siehe die
Seiten
Das Problem kann daher wie folgt formuliert werden:
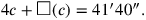
|
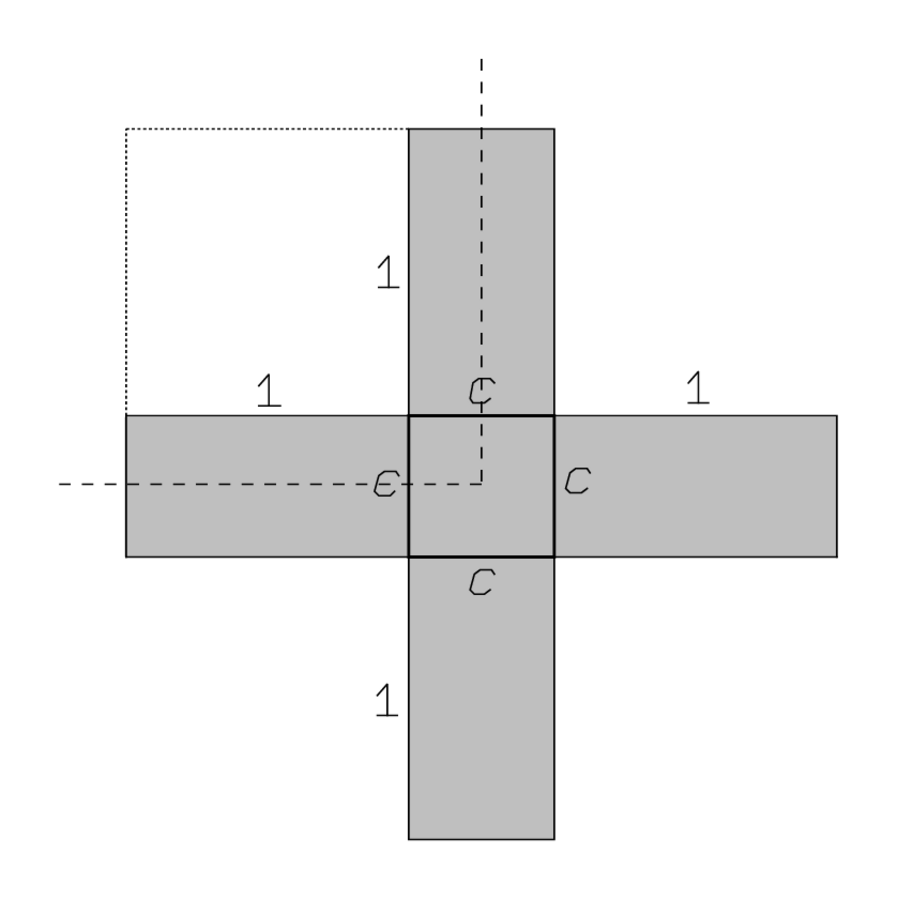
Abb. 4.12 macht das Verfahren klar: 4c
wird durch 4 Rechtecke
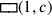 dargestellt;
die Summe 41′40″ entspricht daher der kreuzförmigen Figur bei der
eine „Projektion“ in jede der vier Himmelsrichtungen verläuft.
dargestellt;
die Summe 41′40″ entspricht daher der kreuzförmigen Figur bei der
eine „Projektion“ in jede der vier Himmelsrichtungen verläuft.
Zeilen 12-13 verlangen,
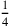 des Kreuzes (mit gestrichelten
Linien dargestellt) herauszuschneiden und eine quadratische Ergänzung
des Kreuzes (mit gestrichelten
Linien dargestellt) herauszuschneiden und eine quadratische Ergänzung
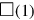 zum daraus resultierenden Gnomon „hinzuzufügen“.
Es gibt keinen Grund, etwas „enthalten zu lassen“, weil die Seiten
des ergänzenden Quadrats bereits an der richtigen Stelle sind. Wir bemerken
allerdings, dass die „Projektion“ selbst „hinzugefügt“
wird: es ist also keine bloße Zahl mehr, sondern eine quadratische Figur
identifiziert durch ihre Seite.
zum daraus resultierenden Gnomon „hinzuzufügen“.
Es gibt keinen Grund, etwas „enthalten zu lassen“, weil die Seiten
des ergänzenden Quadrats bereits an der richtigen Stelle sind. Wir bemerken
allerdings, dass die „Projektion“ selbst „hinzugefügt“
wird: es ist also keine bloße Zahl mehr, sondern eine quadratische Figur
identifiziert durch ihre Seite.
Die Vervollständigung
Die Methode ist derart verschieden von allen anderen Texten, dass Neugebauer
Der archaisierende Aspekt, das sei noch bemerkt, dominiert nicht vollständig. Zeile 12,
welche zuerst das „Einschreiben“ der 4 verlangt und danach sein
igi
TMS VIII #1
(1)Die Fläche 10′. Das 4tel der Breite zur Breite habe ich hinzugefügt, bis 3 bin ich gegangen, über
(2)die Länge geht es 5′ hinaus. Du, 4, vom Viertel, so viel als Breite setze. Das Viertel von 4 nimm, 1 siehst Du.
(3)1 bis 3 gehe, 3 siehst Du. 4 Viertel der Breite zu 3 füge hinzu, 7 siehst Du.
(4)7 so viel als Länge setze. 5′, das darüber Hinausgehende, zum Herauszureißenden der Länge setze. 7, von der Länge, auf 4, ¿von der Breite?, erhöhe,
(5)28 siehst Du. 28, von den Flächen, auf 10′ die Fläche erhöhe, 4°40′ siehst Du.
(6)5′, das Herauszureißende der Länge, auf vier, von der Breite, erhöhe,
20′ siehst Du.
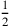 breche, 10′ siehst Du.
10′ lasse enthalten
breche, 10′ siehst Du.
10′ lasse enthalten
(7)1′40″ siehst Du. 1′40″ zu 4°40′ füge hinzu, 4°41′40″ siehst Du. Was ist gleich? 2°10′ siehst Du.
(8)10′ ¿ ...? zu 2°10′ füge hinzu, 2°20′ siehst Du. Was zu 28, von den Flächen, soll ich setzen, das mir 2°20′ gibt?
(9)5′ setze. 5′ auf 7 erhöhe, 35′ siehst Du. 5′, das Herauszureißende der Länge, aus 35′ reiße heraus,
(10)30′ siehst Du, 30′ die Länge. 5′ die Länge, auf 4 von der Breite erhöhe, 20′ siehst Du, 20 die Länge (fehlerhaft für Breite).
In BM 13901 #12
In Symbole übersetzt ist das Problem das Folgende:
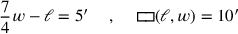
|
(„bis 3 bin ich gegangen“ in Zeile 1 bedeutet, dass das
„Hinzufügen“ von
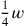 in Zeile 1 dreimal wiederholt
wird) Das Problem hätte mit denselben Methoden gelöst werden können wie auf
TMS IX #3
in Zeile 1 dreimal wiederholt
wird) Das Problem hätte mit denselben Methoden gelöst werden können wie auf
TMS IX #3
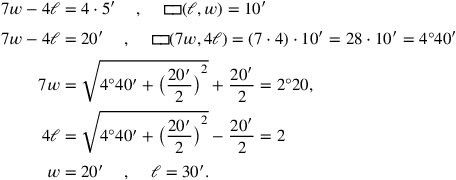
|
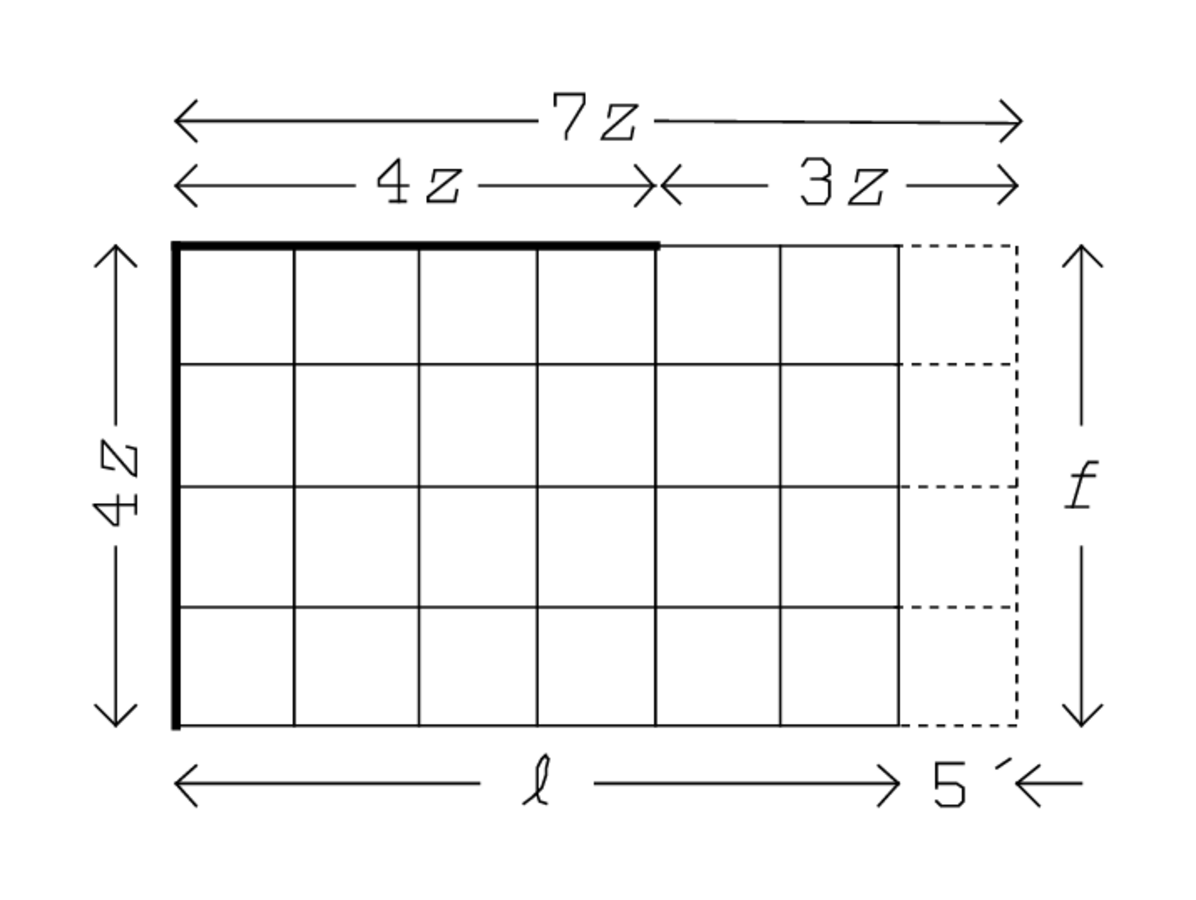
Einmal mehr zeigt der Rechner jedoch, dass er
mehrgleisig fahren kann und zwischen verschiedenen Varianten die ihm
genehmste wählen kann.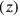 gleich
gleich
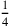 der Breite ist (siehe
Abbildung 4.13). Auf diese Weise sorgt er dafür, dass die Breite
4 ist, verstanden als 4
der Breite ist (siehe
Abbildung 4.13). Auf diese Weise sorgt er dafür, dass die Breite
4 ist, verstanden als 4
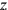 (Du, 4, vom Viertel, so viel als
Breite setze), und dass die Länge, verlängert um 5′, gleich 7 ist,
verstanden als 7z (7 so viel als Länge setze). Zeile 4 findet,
dass das Rechteck mit den Seiten 7
(Du, 4, vom Viertel, so viel als
Breite setze), und dass die Länge, verlängert um 5′, gleich 7 ist,
verstanden als 7z (7 so viel als Länge setze). Zeile 4 findet,
dass das Rechteck mit den Seiten 7
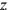 und 4
und 4
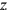 – mit
anderen Worten, das ursprüngliche Rechteck verlängert um 5′ –
aus
– mit
anderen Worten, das ursprüngliche Rechteck verlängert um 5′ –
aus
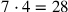 kleinen Quadraten
kleinen Quadraten
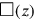 besteht10.
Diese 28 Quadrate übertreffen die Fläche 10′ um eine gewisse
Anzahl von Seiten (
besteht10.
Diese 28 Quadrate übertreffen die Fläche 10′ um eine gewisse
Anzahl von Seiten (
 ), deren Bestimmung auf später verschoben
wird. Wie üblich wird das nicht normalisierte Problem
), deren Bestimmung auf später verschoben
wird. Wie üblich wird das nicht normalisierte Problem
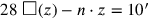
|
in
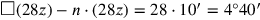
|
verwandelt.
Zeile 6 findet
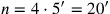 , und von hier an folgt alles dem
üblichen Schema, wie man in Abbildung 4.14 sehen kann:
28
, und von hier an folgt alles dem
üblichen Schema, wie man in Abbildung 4.14 sehen kann:
28
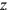 wird gleich 2°20′, und
wird gleich 2°20′, und
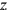 folglich gleich
5′.11
Also ist die Länge
folglich gleich
5′.11
Also ist die Länge
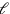 gleich
gleich
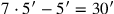 , und
die Breite
, und
die Breite
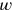 gleich
gleich
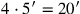 .
.
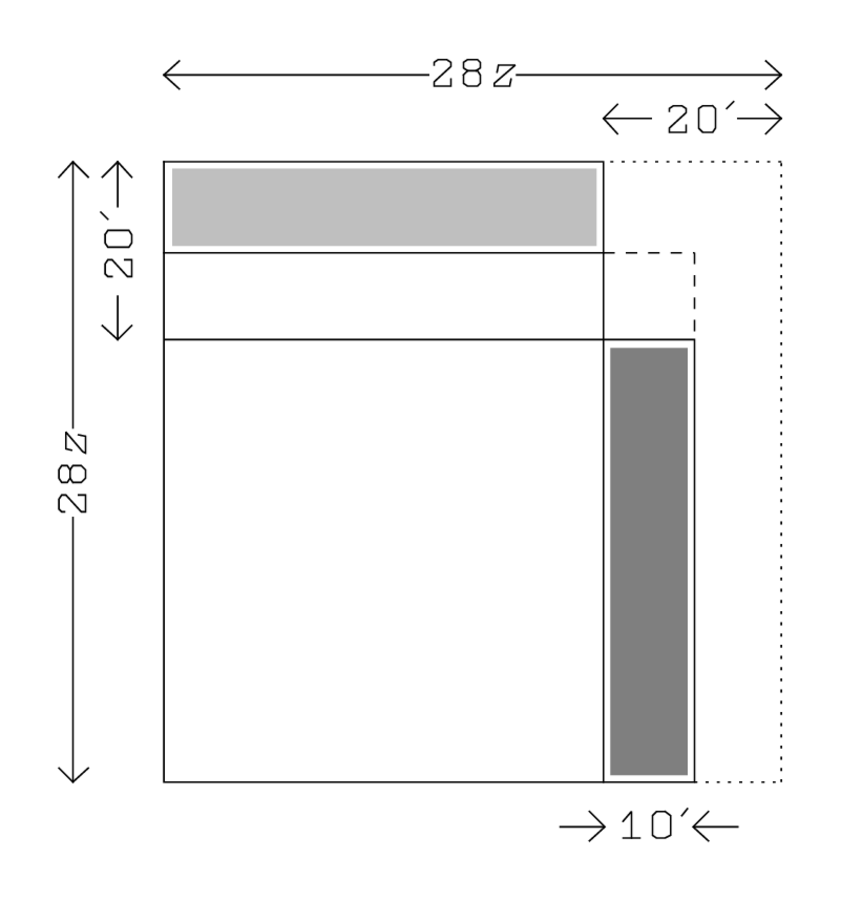
Abb. 4.14: Lösung der normalisierten Gleichung von TMS VIII #1.
YBC 6504 #4
Rs.
(11)So viel wie die Länge über die Breite hinausgeht, gegenüber gestellt, aus dem Innern der Fläche habe ich herausgerissen:
(12)8′20″. 20′ die Breite, seine Länge was?
(13)20′ stelle gegenüber: 6′40″ setze.
(14)6′40″ zu 8′20″ füge hinzu: 15′ setze.
(15)Bei 15′, 30′ ist gleich. 30′, die Länge, setze.
Bis jetzt waren alle Texte, die wir betrachtet haben, mathematisch korrekt,
abgesehen von einigen wenigen Berechnungen und
Kopierfehlern.
Der vorliegende Text ist ein Beispiel hierfür. Übersetzt in die moderne Symbolsprache ist das Problem das folgende:
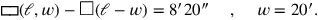
|
Erstaunlicherweise wird die Länge gefunden als das, was bei
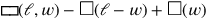
|
„gleich ist“, also nach einer Umformung und in
Symbolen ausgedrückt durch
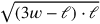 .
.
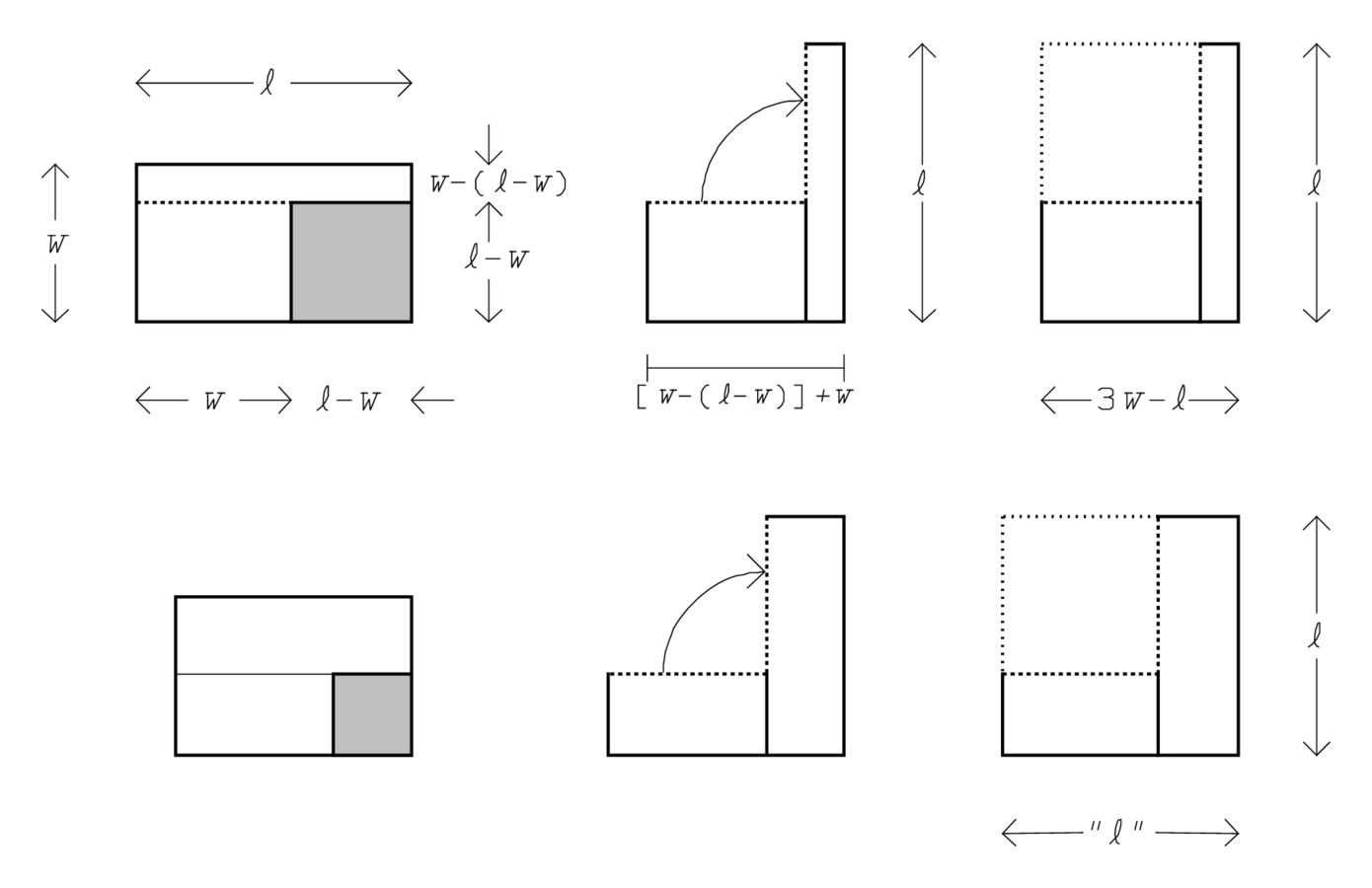
Abb. 4.15: Die cut-and-paste Operationen auf YBC 6504 #4.
Der Fehler scheint schwer erklärbar zu sein, aber eine Betrachtung
der Geometrie des Arguments enthüllt dessen Ursprung (siehe Abb. 4.15).
Oben ist das Verfahren (nicht maßstabsgetreu) dargestellt; wir sehen, dass
das „Hinzufügen“ von
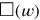 voraussetzt, dass das
verstümmelte Rechteck entlang der gestrichelten Linie zerschnitten wird und
als Pseudo-Gnomon gelegt wird. Es ist klar, dass das Ergebnis der
Vervollständigung
voraussetzt, dass das
verstümmelte Rechteck entlang der gestrichelten Linie zerschnitten wird und
als Pseudo-Gnomon gelegt wird. Es ist klar, dass das Ergebnis der
Vervollständigung 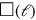 ist, sondern, wenn man richtig zählt,
ist, sondern, wenn man richtig zählt,
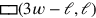 .
.
Unten sehen wir dasselbe, aber jetzt maßstabsgetreu, und jetzt fällt der Fehler
nicht mehr ins Auge. Hier ist
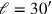 und
und
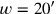 , folglich
, folglich
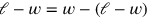 . Daher erscheint das verstümmelte Rechteck als wirkliches
Gnomon, und die vervollständigte Figur entspricht
. Daher erscheint das verstümmelte Rechteck als wirkliches
Gnomon, und die vervollständigte Figur entspricht
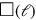 – aber nur
wegen
– aber nur
wegen
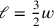 .
.
Dieser Fehler illustriert einen wichtigen Aspekt der
„naiven“
Fußnoten
Was das „Hinzuzufügende“
auf Seite
Wir sollten bemerken, dass die Hälfte, die hier erscheint, wie jeder andere Bruch behandelt wird, gleichberechtigt mit dem darauf folgenden Drittel. Es ist nicht eine „Halbe“, und der Text findet das Resultat durch Multiplikation mit 30′, und nicht durch „zerbrechen“.
Wir sollten ebenfalls bemerken, dass die Hälfte der
Länge und das Drittel der Breite zur Fläche „hinzugefügt“ werden
und nicht angehäuft. Ein paar andere frühe Texte teilen diese Besonderheit.
Es scheint, dass die Feldmesser sich „breite Linien“
vorgestellt haben, also Streifen, von denen
stillschweigend angenommen wurde, dass sie 1 Längeneinheit Breite haben.
Ein solches Vorgehen ist von vielen prä-modernen Feldmessertraditionen
bekannt, und stimmt gut mit dem babylonischen Verständnis von Flächen als
„dick“ überein, die mit einer impliziten Höhe von 1 kùš
versehen sind (wie in der Metrologie von Volumina vorgegeben, welche mit
der von Flächen übereinstimmt – siehe Seite
Die Abwesenheit dieses Begriffs im Text sollte uns nicht davon abhalten, ihn als technischen allgemeingültigen Ausdruck zu verwenden.
Wir können nicht wirklich ausschließen, dass der Text
nicht direkt die Konstruktion beschreibt, sondern sich zweimal auf die
Einschreibung von 3°25′ auf einer Hilfstafel bezieht, gefolgt
vom numerischen Produkt – siehe oben,
Fußnote 11, Seite
Die Lage der „oberen“ Breite auf der linken Seite eine Folge der neuen Ausrichtung der Keilschrift (eine Drehung von 90° gegen den Uhrzeigersinn), die im Kasten „Keilschrift“ erwähnt wird. Die Drehung der Tafeln fand weit vor der altbabylonischen Epoche statt; als Folge davon schrieb man dann von links nach rechts. Aber die altbabylonischen Schreiber wussten genau, dass die wahre Richtung vertikal nach unten war - feierliche Inschriften auf Stein (zum Beispiel das Gesetz von Hammurabi) wurden noch in diesem Stil geschrieben. Es kann gut sein, dass die Schreiber ihre Tafeln zum Lesen um 90° im Uhrzeigersinn gedreht haben.
Diese Unterscheidung zwischen den beiden Halben, von denen eine „(liegen) gelassen“ wird, ist bemerkenswert als weiterer Beweis der geometrischen Interpretation – diese Nomenklatur macht absolut keinerlei Sinn, wenn man sie nicht im räumlichen Sinne versteht.
In Zeile 30 des Textes steht fälschlich 1′57″46‴40⁗ statt 1′57″21‴40⁗: offenbar wurde ein Teilprodukt 25 aus Versehen doppelt addiert. Dies zeigt, dass die Rechnung mit einem Hilfsmittel gemacht worden ist, bei welchem Teilprodukte nach der Addition nicht mehr sichtbar waren. Damit ist eine schriftliche Rechnung auf einer Tontafel ausgeschlossen und legt die Benutzung einer Art Rechenbrett (Abakus) nahe.
Der Fehler wird in die darauffolgenden Zeilen übernommen, verschwindet aber beim Ziehen der Quadratwurzel in Zeile 31, welche daher schon im Voraus bekannt gewesen sein musste.
Im Original ist das Wort „Fläche“ durch eine phonetische Ergänzung markiert, die den Akkusativ anzeigt. Ein Akkusativ in dieser Position hat keine Parallele, und scheint keine andere Interpretation zu erlauben als die hier gegebene.
Hier entspricht der bestimmte Artikel tatsächlich dem Akkadischen, nämlich zu einem Ausdruck der nur benutzt wird, um über eine untrennbare Vielfachheit (so wie die „vier Enden der Erde“ oder „die sieben Todsünden“) zu reden.
Die Benutzung der Multiplikation durch „Erhöhen“
zeigt, dass der Rechner kein neues Rechteck konstruiert,
sondern sein Verfahren auf eine Unterteilung des bereits vorhandenen aufbaut –
siehe die Diskussion und die Ausschaltung einer möglichen alternativen
Interpretation des Verfahrens von BM 13901 #10
in Fußnote 5, Seite
Zeile 10 spricht davon als 5′ die Länge – nämlich der Seite des kleinen Quadrats. Einige andere Texte aus Susa sprechen ebenfalls von der Seite eines Quadrats als seiner „Länge“.