Die Aufgaben, die wir in Kap. 2-5 präsentiert haben, waren so unterschiedlich, dass es notwendig war, jede mit einem ausführlichen Kommentar zu versehen. Um den Lesern, die das möchten, die Untersuchung altbabylonischer Texte zu ermöglichen, ohne dabei fest bei der Hand gehalten zu werden, enthält dieser Anhang die Übersetzung einiger Aufgaben, nur von den absolut notwendigen Erklärungen begleitet. Einige sind Gegenstücke zu Aufgaben, die oben präsentiert wurden und von denselben Tafeln stammen.
TMS XVI #2
(13)Das 4tel der Breite zu dem, was die Länge über die Breite geht, hinzufügen,
(14)15′. Du, 15′ auf 4 erhöhe, 1 siehst Du, was ist es?
(15)4 und 1 setze.
(16)15′ zerstreue. 10′, was darüber hinausgeht, und 5′, das Hinzugefügte, setze. 20′, die Breite,
(17)auf 10′, was darüber hinausgeht, füge hinzu, 30′ die Länge, und 20′, zum Herausreißen, setze. 5′ auf 4 erhöhe,
(18)20′ siehst Du. 20′, die Breite, auf 4 erhöhe, 1°20′ siehst Du.
(19)30′, die Länge, auf 4 erhöhe, 2 siehst Du. 20′, die Breite,
(20)aus 1°20′ reiße heraus, 1 siehst Du. 1
(21)aus 2, der Länge, reiße heraus, 1 siehst Du, was ist es?
(22)Aus 4, vom Viertel, 1 reiße heraus, 3 siehst Du. igi 4 spalte ab, 15′ siehst Du.
(23)15′ auf 3 erhöhe, 45′ siehst Du, so viel wie Breiten, setze. Setze zum Herausreißen.
(24)1 so viel wie Längen setze. [...] 1 nimm, auf 1 Länge
(25)erhöhe, 30′ siehst Du. 20′ die Breite, 20′ auf 45′, (so viel wie (es gibt) von) Breiten, erhöhe,
(26)15′ siehst Du, 15′ zu 15′ füge hinzu, 30′ siehst Du, 30 die Länge.
Kommentar: siehe #1 derselben Tafel, Seite
TMS VII #1
(1)Das Viertel der Breite zur Länge habe ich hinzugefügt, dessen 7⟨tel⟩ zu 10 bin ich gegangen,
(2)so viel wie der Haufen von Länge und ⟨Breite⟩. Du, 4 setze; 7 setze;
(3)10 setze; 5′ zu 7 erhöhe, 35′ siehst Du.
(4)30′ und 5′ trenne. 5′, den Schritt, auf 10 erhöhe,
(5)50′ siehst Du. 30′ und 20′, setze. 5′, den Schritt, auf 4, vom Viertel der Breite,
(6)erhöhe: 20′ siehst Du, 20′, die Breite. 30′ auf 4, vom Viertel
(7)erhöhe, 2 siehst Du. 2 setze, Längen. 20′ aus 20′ reiße heraus,
(8)und aus 2, 30′ reiße heraus, 1°30′ siehst Du.
(9)Aus 4, vom Viertel, 1 reiße heraus, 3 {…} siehst Du.
(10)igi 3 spalte ab, 20′ siehst Du. 20′ auf 1°30′ erhöhe:
(11)30′ siehst Du, 30′ die Länge. 30′ aus 50′ reiße heraus 20′ siehst Du, 20′ die Breite.
(12)Kehre um. 7 auf 4, vom Viertel, erhöhe, 28 siehst Du.
(13)10 aus 28 reiße heraus, 18 siehst Du. igi 3 spalte ab,
(14)20′ siehst Du. 20′ auf 18 erhöhe, 6 siehst Du, 6 (für) die Länge.
(15)6 aus 10 reiße heraus, 4 (für) die Breite. 5′ auf 6 erhöhe,
(16)30′ die Länge. 5′ auf 4 erhöhe, 20′ siehst Du, 20′ die ⟨Breite⟩.
Kommentar: siehe #2 derselben Tafel, Seite
VAT 8389 #1
Vs. I
(1)Von 1 bùr 4 gur Getreide habe ich (als Pachtzins) genommen,
(2)von 1 zweiten bùr 3 gur Getreide habe ich genommen.
(3)Getreide über Getreide, 8‵20 ging es darüber hinaus.
(4)Meine Felder habe ich angehäuft: 30‵.
(5)Meine Felder was?
(6)30‵, das bùr, setze. 20‵, das Getreide, das er genommen hat, setze.
(7)30‵, das zweite bùr, setze
(8)15‵, das Getreide, das er genommen hat,
(9)8‵20 welches das Getreide über das Getreide hinausging,
(10)und 30‵ der Haufen der Flächen der Felder, setze:
(11)30‵ der Haufen der Flächen der Felder
(12)brich entzwei: 15‵.
(13)15‵ und 15‵ bis zweimal setze:
(14)igi 30‵, vom bùr, spalte ab: 2″.
(15)2″ auf 20‵, das Getreide, das er genommen hat,
(16)erhöhe, 40′ das falsche Getreide; auf 15‵ welches bis zwei Mal
16a.Du gesetzt hast,
(18)erhöhe, 10‵ möge Dein Kopf halten!
(19)igi 30, vom zweiten bùr, spalte ab, 2″.
(20)2″ auf 15‵, das Getreide
(21)erhöhe, 30′ das falsche Getreide; auf 15 welches bis zwei Mal
20a.Du gesetzt hast, erhöhe, 7‵30.
(23)10‵ welches Dein Kopf hält,
(24)über 7‵30 was geht es hinaus? 2‵30 geht es darüber hinaus.
(25)2‵30 welches es darüber hinausgeht, aus 8‵20
(26)welches das Getreide über das Getreide hinausgeht,
Vs. II
(1)reiße heraus: 5‵50 hinterlässt Du.
(2)5‵50, welche Du hinterlassen hast,
(3)möge Dein Kopf halten!
(4)40′, die Änderung, und 30′, die Änderung
(5)häufe an: 1°10′. Das igi kenne ich nicht.
(6)Was zu 1°10′ muss ich setzen,
(7)das mir 5‵50, was Dein Kopf hält, gibt?
(8)5‵ setze. 5‵ auf 1°10 erhöhe.
(9)5‵50 gibt es Dir.
(10)5‵ welche Du gesetzt hast, aus15‵ welche bis zwei Mal
(11)Du gesetzt hast, aus eins reiße heraus,
(12)zu eins füge hinzu:
(13)Das erste ist 20‵, das zweite ist 10‵.
(14)20‵ die Fläche des ersten Felds, 10‵ die Fläche des zweiten Felds.
(15)Wenn 20‵ die Fläche des ersten Felds,
(16)10‵ die Fläche des zweiten Felds, ihr Getreide was?
(17)igi 30‵, vom bùr, spalte ab: 2″.
(18)2″ auf 20‵, das Getreide, das er genommen hat,
(19)erhöhe, 40′. Auf 20‵, die Fläche des ersten Felds,
(20)erhöhe, 13‵20 das Getreide von 20‵, die Fläche des zweiten Felds.
(21)igi 30‵, vom zweiten bùr, spalte ab: 2″.
(22)2″ auf 15‵, das Getreide, das er genommen hat, erhöhe, 30′.
(23)30′ auf 10‵, die Fläche des zweiten Felds
(24)erhöhe, 5 das Getreide der Fläche des zweiten Felds.
(25)13‵30 das Getreide der ¿Fläche? des ersten Felds
(26)über 5 das Getreide ¿der Fläche? des zweiten Felds
(27)was geht es darüber hinaus? 8‵20 geht es darüber hinaus.
Diese Aufgabe stammt von einer von zwei Zwillingstafeln, die
insgesamt zehn Probleme über die Pacht enthält, die für zwei Felder bezahlt werden.
Auf einem Feld ist die Pacht 4 gur
Wie auf Seite
Heutige Leser mögen es seltsam finden, dass
die beiden Pachten pro bùr, die in Zeilen I.1-2 in
gur (pro bùr) angegeben sind, in den Zeilen I.6-7
ohne Multiplikation in sìla umgerechnet sind; im Allgemeinen
überspringt der Text, wie wir sehen werden, keine Zwischenschritte.
Die Erklärung ist, dass die Umrechnung mit Hilfe einer
„metrologischen Tabelle“
Heutige Leser dürften sich ebenfalls darüber wundern, dass der Text nicht ein,
sondern zwei Mal den Wert eines bùr in sìla und dessen igi
angibt. Einmal mehr ist der Grund dafür der, dass der Text eine altbabylonische
Rechentechnik sìla pro sar).
sìla pro sar).
Eine kleine Erklärung erscheint angebracht, um das Verständnis des Verfahrens
zu erleichtern. Der Text bestimmt zuerst, wie groß die Differenz zwischen den
beiden Pachten wäre, wenn die beiden Felder die gleiche Fläche hätten, also
jedes 15‵ sar. Dieser Unterschied ist nicht groß genug: er
beträgt 2‵30 sìla, 5‵50 sìla zu
wenig – und folglich muss das erste Feld vergrößert werden. Jedes Mal, wenn
ein sar vom zweiten zum ersten Feld dazugegeben wird, wächst die
Differenz um 40′+30′ sìla (die beiden
„Änderungen“
Am Schluss finden wir eine numerische Verifikation
VAT 8390 #1
Vs. I
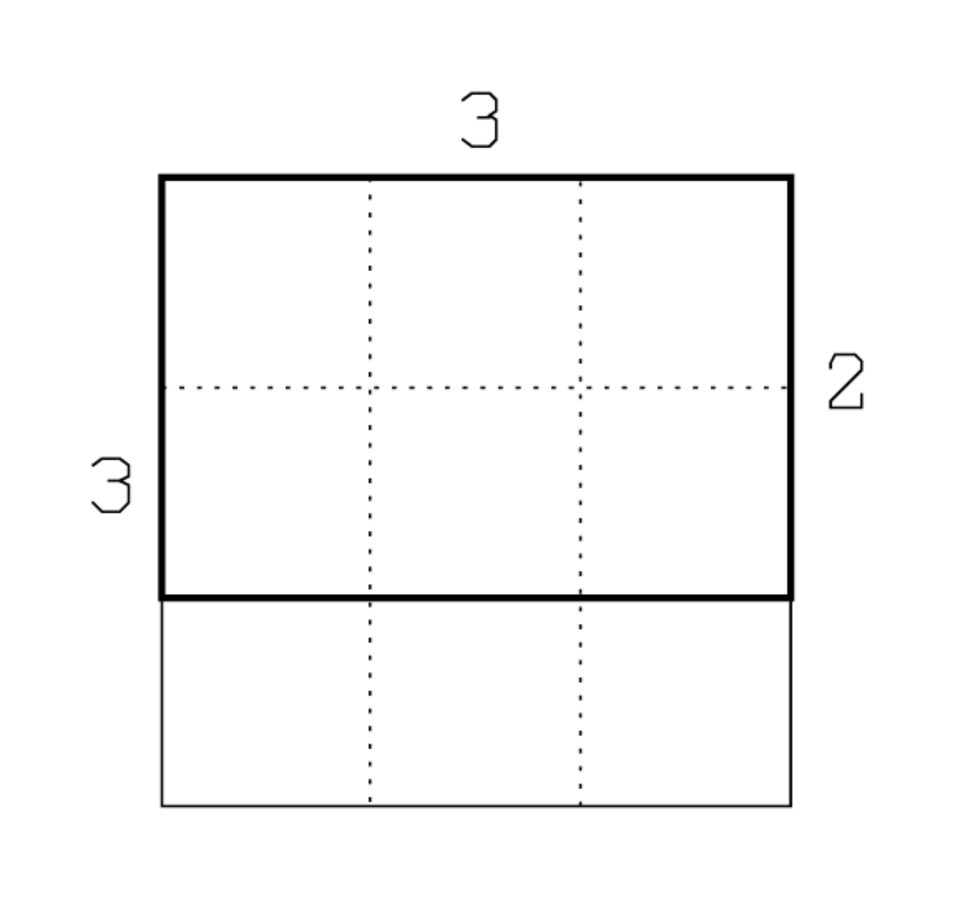
(1)Länge und Breite habe ich enthalten lassen: 10‵ die Fläche.
(2)Die Länge zu sich selbst habe ich enthalten lassen:
(3)eine Fläche habe ich gebaut.
(4)So viel wie die Länge über die Breite hinausging
(5)habe ich enthalten lassen, bis 9 habe ich wiederholt:
(6)so viel wie jene Fläche welche die Länge mit sich selbst
(7)enthalten lassen worden ist.
(8)Die Länge und die Breite was?
(9)10‵ die Fläche setze,
(10)und 9 (bis zu) was er wiederholt hat, setze:
(11)Die Gleichseite von 9 bis zu der er wiederholt hat, was? 3.
(12)3 zur Länge setze,
(13)3 zur Breite setze.
(14)Weil er „so viel wie die Länge über die Breite hinausging,
(15)habe ich halten lassen,” gesagt hat,
(16)1 aus 3, welche Du zur Breite gesetzt hast,
(17)reiße heraus: 2 hinterlässt Du.
(18)2 welche Du hinterlassen hast, zur Breite setze.
(19)3 welche Du zur Länge gesetzt hast,
(20)auf 2 welche Du ⟨zur⟩ Breite gesetzt hast, erhöhe: 6.
(21)igi 6 spalte ab: 10′.
(22)10′ auf 10‵ die Fläche
(23)Die Gleichseite von 1‵40 was? 10.
Vs. II
(1)10 zu 3, welche Du zu der Länge gesetzt hast,
(2)erhöhe; 30 die Länge.
(3)10 zu 2 welche Du zur Breite gesetzt hast,
(4)erhöhe, 20 die Breite.
(5)Wenn 30 die Länge, 20 die Breite,
(6)die Fläche was?
(7)30 die Länge zu 20 die Breite erhöhe, 10‵ die Fläche.
(8)30 die Länge zusammen mit 30 lasse enthalten: 15‵.
(9)30 die Länge über 20 die Breite, was geht sie hinaus? 10 geht sie hinaus.
(10)10 zusammen mit 10 lasse enthalten: 1‵40.
(11)1‵40 bis 9 wiederhole: 15‵ die Fläche.
(12)15‵ die Fläche, so viel wie 15‵ die Fläche welche die Länge
(13)mit sich selbst enthalten lassen worden ist.
Das folgende Diagramm (Abb. 1) dient zur Unterstützung der Interpretation
Der Text erklärt sich dann fast von selbst, insbesondere wenn man sich an
BM 13901 #10
Man sollte die Benutzung der multiplikativen Operationen „enthalten lassen“,
„erhöhen“ und „wiederholen“
VAT 8520 #1
Vs.
(1)Das 13tel vom Haufen des igûm und des igibûm
(2)bis 6 habe ich wiederholt, vom Innern des igûm
(3)habe ich es abgerissen: 30′ habe ich hinterlassen. 1 die Fläche. Das igûm und das igibûm was?
(4)Weil „das Dreizehntel des Haufens von igûm und igibûm
(5)bis 6 habe ich wiederholt, und vom Innern des igûm
(6)habe ich herausgerissen: 30′ habe ich hinterlassen,“ er gesagt hat,
(7)13, vom Dreizehntel, setze; 6 bis zu welchem er wiederholt hat, setze;
(8)1, die Fläche, setze; und 30′ was er hinterlassen hat, setze.
(9)Aus 13, vom Dreizehntel, 6 bis zu welchem er wiederholt hat,
(10)reiße heraus. 7 hinterlässt Du.
(11)7 die Du hinterlässt und 6 bis zu welchem Du wiederholt hast,
(12)behalte im Kopf!
(13)7 zu 6 erhöhe, 42 zu 1, der Fläche, erhöhe: 42.
(14)42 behalte im Kopf!
(15)13, vom Dreizehntel, auf 30′ was er hinterlassen hat,
(16)erhöhe, 6°30′ brich entzwei: 3°15′.
(17)3°15′ zusammen mit 3°15′ lasse enthalten: 10°33′45″.
(18)Zu 10°33′45″, 42, welches du im Kopf behalten hast,
(19)füge hinzu, 52°33′45″.
(20)Das Gleiche von 52°33′45″ was? 7°15′.
(21)7°15′ und 7°15′, dessen Gegenseite, lege nieder:
(22)3°15′, was Du enthalten lassen hast, vom einen reiße heraus, dem anderen füge hinzu:
(23)Das erste ist 10°30, das andere 4.
(24)Was muss ich zu 7, was Du im Kopf behalten hast, setzen,
(25)das mir 10°30′ gibt? 1°30′ setze. 1°30′ zu 7 erhöhe,
(26)10°30′ gibt es Dir. 1°30′ das du gesetzt hast, ist das igûm.
(27)igi 6, das Dein Kopf hält, spalte ab, 10′.
(28)10′ zu 4 erhöhe, 40′ ist das igibûm.
(29)Weil 1°30′ das igûm ist, 40′ das igibûm, die Fläche ist was?
(30)1°30′, das igûm, zu 40′, dem igibûm, erhöhe, 1 ist die Fläche.
(31)1°30, das igûm
Rs.
(1)Das Dreizehntel von 2°10′ was? 10′.
(2)10′ bis 6 wiederhole: 1, von 1°30,
(3)dem igûm, reiße heraus: 30′ hinterlässt Du.
Wie YBC 6967
Was die mathematische Struktur und Lösung angeht, vergleiche man mit
TMS IX #3
Erklärung des Übersetzers: Sind x und
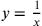 die beiden Reziproken,
gilt also
die beiden Reziproken,
gilt also
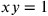 , dann lautet die zweite Bedingung
, dann lautet die zweite Bedingung
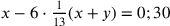 .
Multiplikation mit 13 verwandelt diese in
.
Multiplikation mit 13 verwandelt diese in
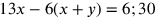 , also
, also
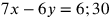 .
.
Str 368
Vs.
(1)Ich habe ein Schilfrohr genommen, sein Maß kenne ich nicht.
(2)1 kùš habe ich abgeschnitten. 1 Sechziger (Schritte entlang) der Länge bin ich gegangen.
(3)Mit dem, was ich abgeschnitten habe, habe ich es vergrößert.
(4)30 (Schritte) damit bin ich (entlang) der Breite gegangen.
(5)6‵15 ist die Fläche. Der Kopf (ursprüngliche Länge) des Schilfrohrs was?
(6)Du, bei Deinem Vorgehen
(7)1‵ und 30 setze. (Für) das Schilfrohr, das Du nicht kennst,
(8)1 setze, auf 1 Sechziger, das Du gegangen bist,
(9)erhöhe: 1‵ ist die falsche Länge.
(10)30 auf diese 1 erhöhe, 30 ist die falsche Breite.
(11)30, die falsche Breite, auf 1‵, die falsche Länge,
(12)erhöhe, 30‵ die falsche Fläche.
(13)30‵ auf 6‵15, die wahre Fläche,
Rs.
(1)erhöhe: 3‷7‶30‵ gibt es Dir.
(2)5′ welche Du abgeschnitten hast, auf die falsche Länge erhöhe,
(3)5 gibt es Dir. 5 auf die falsche Breite erhöhe,
(4)2‵30 gibt es Dir.
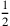 von 2‵30 brich ab, 1‵15
von 2‵30 brich ab, 1‵15
(5)1‵15 stelle gegenüber, 1‶33‵45
(6)zu 3‷7‶30‵ füge hinzu, 3‷9‶3‵45.
(7)Was ist gleich? 13‵45 ist gleich.
(8)1‵15 welches Du gegenüber gestellt hast, zum Innern füge hinzu,
(9)15‵ gibt es Dir. igi 30‵,
die falsche Fläche
(10)2″ auf 15‵ erhöhe, 30′ ist der Kopf des Schilfrohrs.
Dies ist die Rechtecksversion des „abgebrochenen Schilfrohrs“
YBC 6504 #1
Vs.
(1)So viel wie Länge über Breite hinausgeht, habe ich gegenüber gestellt, vom Innern der Fläche
(2)habe ich es herausgerissen: 8′20″. Länge über Breite, 10′ geht sie hinaus.
(3)Bei Deinem Verfahren, 10′ lasse enthalten:
(4)1′40″ zu 8′20″ füge hinzu: 10′ setzt Du.
(5)Die Hälfte von 10′ brich ab: 5′ setzt Du.
(6)5′ lasse enthalten: 25″ setzt Du.
(7)25″, die Fläche, zu 10′ füge hinzu: 10′25″ setzt Du.
(8)Bei 10′25″, 25′ ist gleich. 5′ zu 25′ füge hinzu:
(9)30′, die Länge, setzt Du. 5′ aus 25′ reiße heraus:
(10)20′, die Breite, setzt Du.
Diese Aufgabe dreht sich um dasselbe verstümmelte Rechteck wie
#4 derselben Tafel (siehe Seite
Bei dieser ersten Aufgabe kennen wir die Seite des Quadrats, das
„herausgerissen“ worden ist. Man kann sie daher leicht
auf den Typ reduzieren, den wir von YBC 6967
Hier geht das „Hinzufügen“
YBC 6504 #3
Rs.
(1)So viel wie Länge über ⟨Breite⟩ hinausgeht, gegenübergestellt, aus dem Inneren der Fläche habe ich herausgerissen,
(2)8′20″. 30′ die Länge, seine Breite, was?
(3)30′ gegenübergestellt: 15′ setzt Du.
(4)8′20″ aus dem Innern von 15′ reißt Du heraus, 6′40″ setzt Du.
(5)Die Hälfte von 30′ brichst Du:
(6)15′ gegenübergestellt: 3′45″ setzt Du.
(7)3′45″ zu 6′40″ fügst Du hinzu: 10′25″ setzt Du.
(8)Bei 10′25″, 25′ ist gleich. 15′ aus 25′ reißt Du heraus:
(9)10′ setzt Du. 10′ aus 30′ reißt Du heraus:
(10)20′, die Breite, setzt Du.
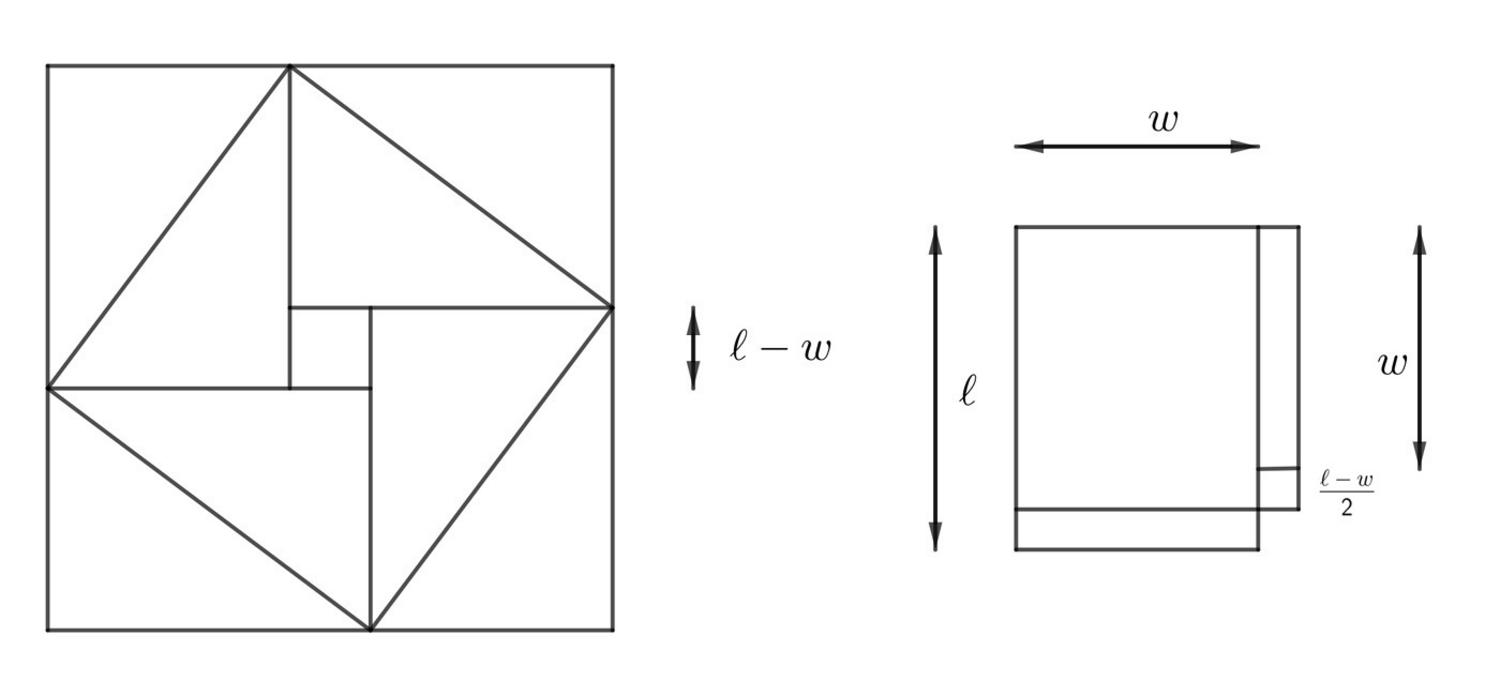
Dies ist das dritte Problem über der Länge lässt einen Rest, der in ein Quadrat
über der Länge lässt einen Rest, der in ein Quadrat
 und ein Rechteck
und ein Rechteck
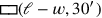 zerlegt werden
kann. Diese beiden können, wie im Diagramm gezeigt, in ein Gnomon verwandelt werden.
Wir können den Prozess als „Wechsel der Variablen“ betrachten – das
Problem dreht sich nun um ein Quadrat
zerlegt werden
kann. Diese beiden können, wie im Diagramm gezeigt, in ein Gnomon verwandelt werden.
Wir können den Prozess als „Wechsel der Variablen“ betrachten – das
Problem dreht sich nun um ein Quadrat
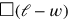 und 30′ seiner Seite,
und seine Lösung folgt der Standardprozedur für solche Fälle.
und 30′ seiner Seite,
und seine Lösung folgt der Standardprozedur für solche Fälle.
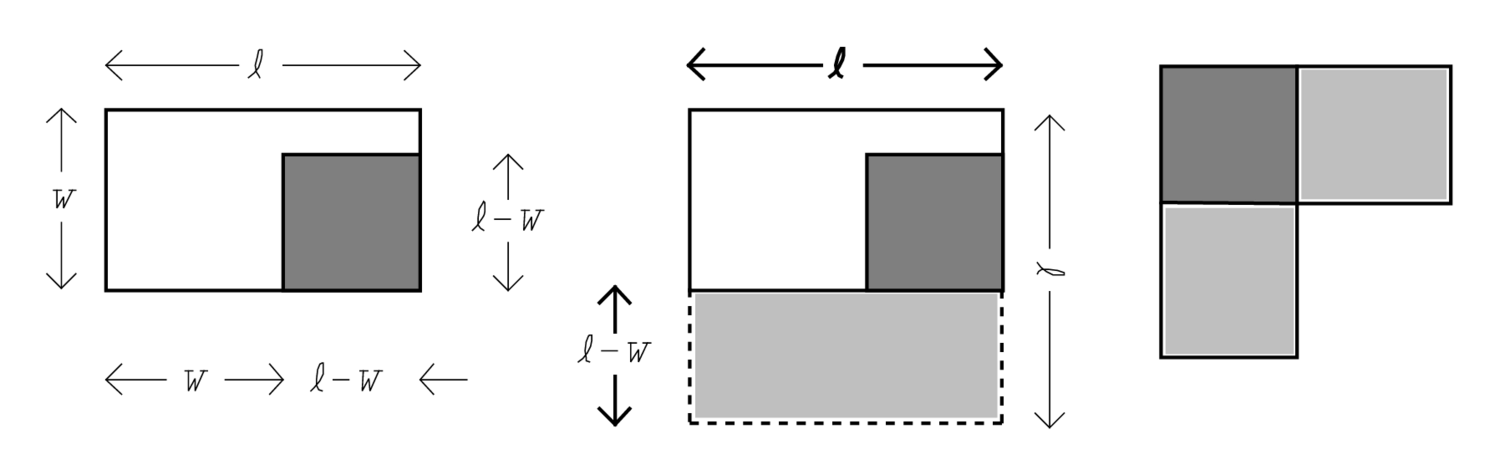
Abb. 2: Die Geometrie hinter YBC 6504 #3, in leicht veränderten Proportionen.
BM 85200+VAT 6599 #23
Rs. I
(19)Eine Ausgrabung. So viel wie ich gegenüber gestellt habe, und 1 kùš, darüber hinausgehend, das ist die Tiefe. 1°45′ Erde habe ich herausgerissen.
(20)Du, 5′, was darüber hinausgeht, auf 1, die Umrechnung, erhöhe, 5′ siehst Du; auf 12 erhöhe, 1 siehst Du.
(21)5′ stelle sich selbst gegenüber, 25″ siehst Du. 25″ auf 1 erhöhe, 25″ siehst Du. igi 25 spalte ab,
(22)2‵24 siehst Du. 2‵24 auf 1°45′ erhöhe, 4‵12 siehst Du.
(23)Von „gleich, 1 hinzugefügt“ 6 ¿1? ist/sind gleich. 6 auf 5′ erhöhe, 30′ siehst Du, steht sich gegenüber. 6 (fehlerhaft für 7) die Tiefe.
(24)Das Verfahren.
Dieses Problem stammt von derselben Tafel wie das
„Ausgrabungsproblem“ erlaubt, welche „gleich, 1 hinzugefügt“
genannt werden.
erlaubt, welche „gleich, 1 hinzugefügt“
genannt werden.
Db2–146
Vs.
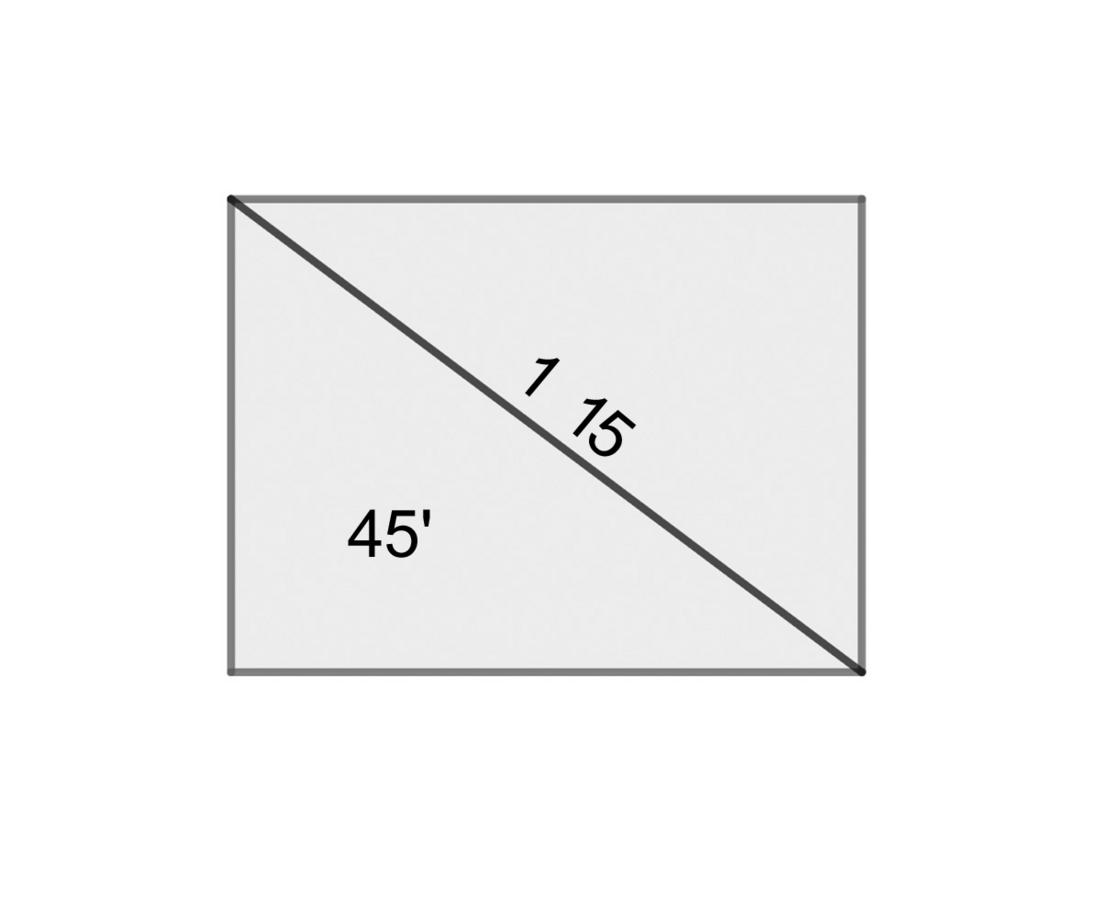
(1)Wenn Dich jemand über eine Diagonale (eines Rechtecks) fragt
(2)so: 1°15 die Diagonale, 45′ die Fläche,
(3)Länge und Breite entsprechend was? Du, bei Deiner Lösung,
(4)1°15′, Deine Diagonale, deren Gegenseite lege nieder,
(5)lasse sie enthalten: 1°33′45″ kommt heraus.
(6)1°33′45″ ¿möge Deine? Hand ¿halten?
(7)45′ Deine Fläche zu Zwei bringe: 1°30′ kommt heraus.
(8)Von 1°33′45″ schneide ab: {…} 3′45″ der Rest.
(9)Das Gleiche von 3′45″ nimm: 15′ kommt heraus. Dessen halber Teil
(10)7′30″ kommt heraus, auf 7′30″ erhöhe: 56″15‴ kommt heraus
(11)56″15‴ Deine Hand. 45′ Deine Fläche über Deiner Hand;
(12)45′56″15‴ kommt heraus. Das Gleiche von 45′56″15‴ nimm:
(13)52′30″ kommt heraus, 52′30″ dessen Gegenseite lege nieder;
(14)7′30″ das Du enthalten lassen hast, zu Eins
(15)füge hinzu, von Eins
(16)schneide ab. 1 Deine Länge, 45 die Breite. Wenn 1 die Länge,
(17)45 die Breite, die Fläche und die Diagonale entsprechend was?
(18)Du, in Deinem Verfahren, lass die Länge enthalten;
(19)1 kommt heraus ...behalte es im Kopf.
Rs.
(20)… : 45′, die Breite, lass enthalten:
(21)33′45″ kommt heraus. Zu Deiner Länge füge hinzu:
(22)1°33′45″ kommt heraus. Das Gleiche von 1°33′45″ nimm:
(23)1°15′ kommt heraus. 1°15′ Deine Diagonale. Deine Länge
(24)auf die Breite erhöhe, 45′ Deine Fläche.
(25)So ist das Verfahren.
Dies ist einer der Texte aus der Gegend von Eshnunna, und er gehört daher zur frühesten Phase (und er benutzt, wie wir sehen, die Phrase „füge zum einen hinzu, schneide vom anderen ab“ und respektiert so die „Konkretheitsnorm“ nicht). Er kann relativ genau auf ca. 1775 v.Chr. datiert werden.
Das Problem ist eines der Rätsel welche die altbabylonische
Schule
In den Zeilen 1-9 wird der Unterschied zwischen der Länge und der Breite des
Rechtecks bestimmt; die Methode ist im oberen Teil von Abb. 4
dargestellt. Danach werden die Seiten aus dieser Differenz und der Fläche
nach der Prozedur bestimmt, die wir bereits sehr gut kennen, etwa von
YBC 6967
Die „Hand“
Am Schluss haben wir eine Probe mit einer unmissverständlichen Spur der „pythagoreischen Regel“ in einer abstrakten Formulierung (die Länge lasse enthalten, ohne die übliche Identifizierung mit ihrem numerischen Wert).
Fußnoten
Die Tafel ist an dieser Stelle beschädigt, aber die Spuren der vorhandenen Zeichens könnten von dem Wort takkirtum stammen, das „Wechsel“ oder „Änderung“ bedeutet, aber nicht in anderen mathematischen Texten auftaucht. Jedenfalls berührt dieser philologische Zweifel nicht die Interpretation des mathematischen Verfahrens.