Eine Möglichkeit, sozio-kulturelle Strukturen und Umstände zu
erklären, argumentiert von ihrer Funktion her: Wenn die
Schreiberschule
Eine andere Art der Erklärung – keine alternative, sondern eher die
andere Seite derselben Medaille – gründet sich auf den historischen
Ursprung:
Während der letzten 40 Jahre haben sich unsere Kenntnisse über die mesopotamische Mathematik des dritten vorchristlichen Jahrtausends stark vermehrt, insbesondere was die Bestimmung rechtwinkliger oder fast rechtwinkliger Felder angeht. Wir können jetzt mit Zuversicht behaupten, dass wir deshalb keine Texte aus dem dritten Jahrtausend mit algebraischen Problemen gefunden haben, weil es keine gegeben hat.
Dies widerspricht der traditionellen Überzeugung, dass alles in Mesopotamien aus vor undenklichen Zeiten stammen muss. Sicher, wir sind im „Orient“, wo alles, wie wir wissen, ohne Alter und Entwicklung (und vor allem ohne Fortschritt) ist – zumindest ist dies im „Westen“ eine Meinung „ohne Alter und Entwicklung“.
Der Ursprung: Rätsel von Feldmessern
Die Algebra der altbabylonischen Schreiberschulen ist, ganz im
Gegenteil, keine Fortsetzung einer jahrhunderte- oder gar
jahrtausendelangen Tradition – im dritten Jahrtausend existierte
nichts Vergleichbares. Dies ist eine unter vielen Charakteristika der
neuen Kultur der Schreiber dieser Epoche
Eine Erfindung innerhalb der Schreiberschulen stimmt aber wenig mit anderen Quellen überein. Insbesondere widerspricht eine solche der Art, wie Probleme und Techniken, die zur selben Familie gehören, in griechischen und mittelalterlichen Quellen auftauchen. Eine genaue Untersuchung aller parallelen Materialien enthüllt eine ganz andere Geschichte – das Material ist zu riesig, um hier eine vollständige Präsentation der Argumente geben zu können, aber ein Teil davon ist in die folgende Diskussion eingewoben.
Die Feldmesser im zentralen Irak (vielleicht auch aus einer größeren Region,
aber dies ist eine Hypothese, was diese frühe Epoche angeht) besaßen eine
Tradition geometrischer Rätsel
Jemand geht zum Markt und kauft 100 Vögel für 100 Dinare. Eine Gans kostet 3 Dinare, ein Huhn 2, und er bekommt 3 Spatzen für einen Dinar. Sag mir, wenn Du ein erfahrener Rechner bist, was er gekauft hat!1
Es gibt viele Lösungen. 5 Gänse, 32 Hühner und 63 Spatzen;
oder 10 Gänse, 24 Hühner und 66 Spatzen usw. Wenn man allerdings ein
Rätsel beantwortet
Die Lösung solcher Rätsel verlangt oft die Anwendung eines besonderen Tricks. Im vorliegenden Fall könnte man etwa bemerken, dass man jedesmal, wenn man eine Gans kauft, 3 Spatzen kaufen muss – das macht 4 Vögel für 4 Dinare – und 3 Spatzen für jedes Paar Hühner – das sind 5 Vögel für 5 Dinare.
Solche „Unterhaltungsaufgaben“
Irgendwann zwischen 2200 und 1800 v. Chr. haben
akkadische Feldmesser den
Trick erfunden, der später „die akkadische Methode“ genannt wurde,
nämlich die quadratische Ergänzung
Eine Gemeinsamkeit dieser Rätsel war die Betrachtung nur solcher Elemente, die
direkt in den Figuren auftauchten – etwa die Seite oder alle
vier Seiten eines Quadrats, niemals aber „die 3-fache Fläche“
oder „
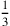 der Fläche“. Man könnte sagen, dass die
Aufgaben ohne Koeffizienten definiert waren, oder alternativ „mit natürlichen
Koeffizienten“.
der Fläche“. Man könnte sagen, dass die
Aufgaben ohne Koeffizienten definiert waren, oder alternativ „mit natürlichen
Koeffizienten“.
Steht
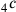 für „die vier Seiten“ und
für „die vier Seiten“ und
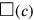 für die Fläche eines Quadrats,
für die Fläche eines Quadrats,
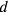 für die Diagonale und
für die Diagonale und
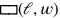 für die Fläche eines Rechtecks, dann scheint
die Liste der Rätsel
für die Fläche eines Rechtecks, dann scheint
die Liste der Rätsel
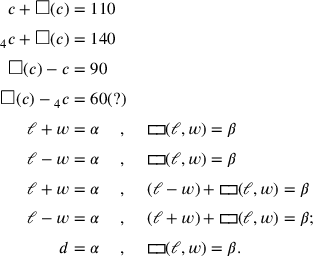
|
Darüber hinaus gab es Probleme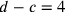 über ein Quadrat, mit der Pseudo-Lösung
über ein Quadrat, mit der Pseudo-Lösung
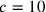 ,
,
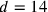 ; bei zwei Aufgaben über
Rechtecke
; bei zwei Aufgaben über
Rechtecke
Diese Rätsel scheinen die altbabylonischen Schreiberschulen übernommen zu
haben
Solche Überlegungen erklären, warum eine Aufgabensammlung über Quadrate wie
BM 13901
Als Folge des Drills der systematischen Variation wurde die Lösung der fundamentalen Probleme allerdings eine Banalität, auf der sich kein professionelles Selbstbewusstsein aufbauen ließ: folgerichtig wurde die Arbeit an komplizierten Problemen nicht nur eine Möglichkeit, sondern geradezu eine kulturelle Notwendigkeit.
Man darf annehmen, dass die Orientierung des Schreiberberufs hin zu einer größeren
Bandbreite von professionellen Verpflichtungen dazu geführt hat, dass man Probleme
außerhalb der abstrakten Geometrie der Feldmessung erfunden hat, bei welchen die
algebraischen Methoden eingesetzt werden konnten, und dass daher, obwohl
„Forschung“ nicht das Ziel einer Schreiberschule gewesen ist, die
Möglichkeiten der Darstellung untersucht wurden. Nach dieser Rekonstruktion
war es also der Transfer zur Schule, welcher der Technik des
cut-and-paste
Andere Veränderungen waren weniger folgenreich, aber dennoch kaum zu übersehen. Die bevorzugte
Seite eines Quadrats in Rätseln war die 10, und dies blieb bis ins sechzehnte Jahrhundert
n. Chr. so. In der Schule war der bevorzugte Wert 30′, und wenn eine antiquierte
Aufgabe 10 beibehielt, dann wurde sie als 10′ interpretiert.6 Schließlich
wurde, wie wir oben auf S.
BM 13901 #23
Es scheint, als hätte die erste Entwicklung der algebraischen Disziplin in der
Gegend von Eshnunna stattgefunden, das nördlich von Babylon liegt, und zwar während
der ersten Jahrzehnte des 18. Jahrhunderts7. Aus dieser Gegend und dieser Zeit
besitzen wir einige mathematische Texte, die ausnahmsweise regulär ausgegraben wurden
und damit datiert werden können. Damals war Eshnunna ein kulturelles Zentrum des ganzen
nördlich-zentralen Teils des heutigen Irak; Eshnunna etnwickelte auch die erste
Gesetzgebung außerhalb des Südens Sumers. Der Text Db2–146
(unten Seite
Etwa um 1761 wurde Eshnunna von Hammurabi erobert und zerstört. Wir wissen, dass Hammurabi
die Idee einer Gesetzessammlung von dort erhielt und dürfen annehmen, dass er auch
versklavte Gelehrte mitbrachte. Ob darunter auch Gelehrte waren, die sich mit dem Unterricht
von Mathematik beschäftigten, können wir nur raten (die
Schichten des zweiten Jahrtausends von Babylon liegen tief unter den Überresten der Stadt des
ersten Jahrtausends), aber jedenfalls übernahm der ehemals sumerische Süden die neue
mathematische Disziplin um etwa 1750 – die Tafel AO 8862
Aufgaben von verschiedenen Grabungsstätten in der Umgebung von Eshnunna drehen sich um viele
der Themen, die aus späteren Zeiten bekannt sind – die frühe Rechtecks-Variante der Aufgabe
vom „abgebrochenen Schilfrohr“, die wir auf Seite
Aus der Zeit wenig später haben wir eine Reihe von Texten, die, nach ihrer Orthographie zu beurteilen, im Süden geschrieben wurden. Einige Textgruppen genügen einem wohldefinierten Kanon, was Format und Terminologie (nicht dieselbe in allen Gruppen) angeht, was ein bewusstes Streben nach Regularität nahelegt (die VAT- und Str-Texte gehören alle hierher). Um 1720 herum trennte sich der ganze Süden jedoch vom altbabylonischen Reich, und danach wurde dort die Schreiberkultur auf ein Minimum reduziert; Mathematik scheint nicht überlebt zu haben. Ab dem späten 17. Jahrhundert haben wir eine nennenswerte Anzahl von Texten aus Sippar, etwas nördlich von Babylon (BM 85200+VAT 6599 ist einer von ihnen), und eine weitere Reihe von Texten aus Susa im westlichen Iran (die TMS-Texte), welche, das legt ihre Terminologie nahe, vom nördlichen, zuerst aus Eshnunna bekannten Typ abstammen. Und danach nichts mehr ...
Das Erbe
Im Jahre 1595 beendete ein Überfall der Hethiter den schon schwachen altbabylonischen Staat und dessen soziales System. Nach dem Überfall übernahmen die Kassiten die Macht, ein Volksstamm, dessen Angehörige als Fremdarbeiter und Plünderer schon seit den Zeiten von Hammurabi in Babylon gelebt hatten. Dies setzte dem altbabylonischen Zeitalter und seiner besonderen Kultur ein abruptes Ende.
Die Schreiberschule
Aus den 1200 Jahren, welche dem Zusammenbruch der altbabylonischen
Kultur folgten, ist kein einziger Algebratext erhalten. Dies hat noch
nicht viel zu bedeuten, weil nur sehr wenige auch nur ansatzweise
mathematische Texte überlebt haben (einige Texte zur Buchhaltung,
Spuren von Feldmessung, einige Tabellen von
Reziproken
Diese späten Texte informieren uns offensichtlich nicht, weder direkt noch indirekt, über die Umgebung in der die Rätsel weitergegeben worden waren, obwohl eine Fortsetzung der Tradition der Feldmesser die plausibelste Erklärung wäre. Quellen aus der klassischen Antike und dem islamischen Mittelalter machen zumindest klar, dass die Tradition, welche einst die altbabylonische Algebra inspiriert hatte, trotz des Verschwindens ihres anspruchsvolleren Nachwuchses überlebt hat.
Der beste Beleg dafür kommt von einem arabischen Handbuch der praktischen
Geometrie
In der griechischen Mathematik  repräsentiert, als „4 Fuß“.
repräsentiert, als „4 Fuß“.
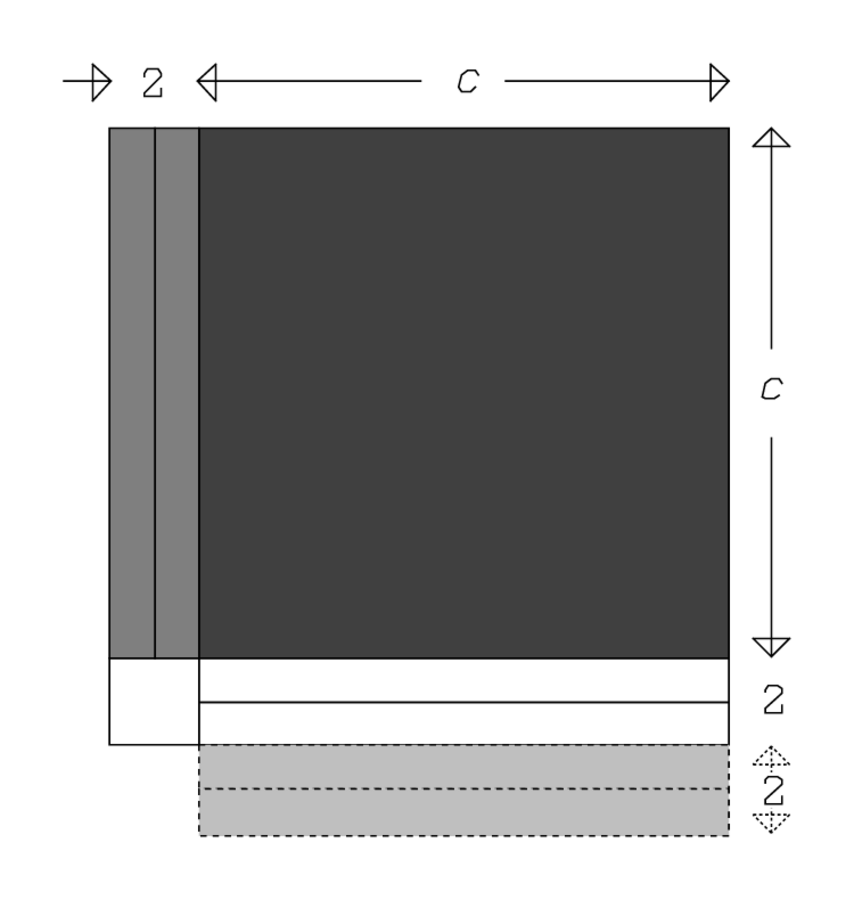
Abb. 8.1: „Die Fläche zum Umfang hinzugefügt“ der Geometrica.
Seit der Entdeckung der babylonischen Algebra wurde oft behauptet,
dass eine Komponente der theoretischen Geometrie der Griechen, nämlich
Prop. II.1-II.10 der Euklidischen
Elemente,
Wenn wir aber die zehn Propositionen II.1–10 der Elemente
mit der Liste der ursprünglichen Rätsel vergleichen, dann machen wir
eine unerwartete Entdeckung: alle zehn Propositionen können direkt mit
der Liste verbunden werden. Sie zeigen, dass die naiven Methoden
der Rätseltradition durch die strengsten theoretischen Standards der Zeit
Euklids begründet werden können.
Die außerordentliche Bedeutung der Elemente in der
Geschichte der Mathematik steht außer Zweifel. Nichtsdestotrotz geht
der wichtigste Einfluss der Feldmessertradition in der modernen
Mathematik auf deren Einwirkung auf die mittelalterliche arabische
Algebra
Auch die arabische Algebra
Du halbierst die Wurzeln, welche in dieser Frage 5 sind. Dann multiplizierst Du diese mit sich selbst, was 25 ergibt; addiere sie zu 39, und es ergibt sich 64. Du sollst daraus die Quadratwurzel ziehen, welche 8 ist. Dann ziehe dies von der halben Wurzel ab, nämlich von 5. Dann bleibt 3 übrig, was die Wurzel des Besitzes ist. Und der Besitz ist 9.
Bereits der Autor der ersten bekannten Abhandlung über Algebra
(die wahrscheinlich erste Abhandlung über dieses
Thema9) –
al-Khwārizmī,
Obwohl also die Algebra der Keilschrifttafeln eine Sackgasse war –
glorreich, aber dennoch eine Sackgasse – waren es die Prinzipien,
welche sie von den ungelehrten Praktikern geborgt hatten, nicht. Ohne
diese Inspiration ist es schwierig zu sehen, wie die moderne
Mathematik
Fußnoten
Dies ist eine „Durchschnittsvariante der Aufgabe. Die Preise variieren ebenso wie die Vogelarten (manchmal handelt es sich auch andere Tiere). Fast immer geht es allerdings um 100 Tiere und 100 Geldeinheiten. Meist sind es drei Tierarten, von denen zwei mehr als einen Dinar kosten und die dritte weniger.
Wer mag, kann versuchen die vollständige Lösung mit oder ohne negative Zahlen (die für verkaufen statt kaufen stehen würden) zu finden und zeigen, dass es eine unter den gegebenen Umständen vollständige Lösung ist. Dies wurde von dem arabischen Mathematiker Abū Kāmil um 900 n. Chr. gemacht. In der Einführung zu seiner Abhandlung darüber nutzte er die Gelegenheit, sich über Praktiker lustig zu machen, denen die theoretische Einsicht fehlte und die nur irgend eine Lösung angaben – und die daher die Frage als Rätsel und nicht als ein mathematisches Problem auffassten.
Siehe den Abschnitt „Schimpfrechnung“ in Christoph Rudolffs Künstliche rechnung mit der ziffer vnd mit den zalpfenningen, Nürnberg 1540.
In altbabylonischen Texten gibt es eine geschlossene Gruppe, welche aus den vier Aufgaben über Rechtecke besteht, bei denen die Fläche zusammen mit der Länge, der Breite, oder ihrer Summe oder Differenz gegeben ist. Wir dürfen annehmen, dass der Trick der quadratischen Ergänzung zuerst erfunden wurde, um die Anzahl dieser Art von Problemen von zwei auf vier zu erhöhen.
Wer eine Algebra der Gleichungen nur deswegen praktiziert, um Lösungen zu finden, hält vielleicht nicht viel von den Koeffizienten – sie sind schließlich nur lästige Dinge, die eliminiert werden sollen. Vieta und seine Generation haben aber die Entfaltung der algebraischen Theorie im 17ten Jahrhundert dadurch ermöglicht, dass sie den Gebrauch allgemeiner Symbole für die Koeffizienten einführten. Entsprechend haben die altbabylonischen Lehrer, als sie Koeffizienten eingeführt haben, die Entwicklung einer algebraischen Methode ermöglicht – ohne dass die Manipulation von Koeffizienten verfügbar und standardisiert ist, ist eine freie Darstellung unmöglich.
Um einzusehen, dass
10 (und 30) genau diese Rolle spielten, muss man zeigen, dass 10 nicht die übliche Wahl in
anderen Situationen war, in denen ein Parameter frei gewählt wurde.
Durch Vergleichen vieler Quellen findet man, dass 10 (oder 30 in Texten, die von der Schultradition
abstammen) die bevorzugte Seitenlänge nicht nur von Quadraten war, sondern auch die anderer Polygone,
genau wie 4, 7 und 11 die bevorzugten Zahlen in Aufgaben zu Vielfachen und Teilern waren, und
zwar nur dort (siehe Fußnote 4, Seite
Eshnunna wurde 2075 von Ur III unterworfen, befreite sich aber bereits 2025 wieder.
Das Liber mensurationum wird einem nicht identifizierten Abū Bakr, „der Heus genannt wird“, zugeschrieben, und wurde von Gerhard von Cremona übersetzt.
Das Zitat stammt aus dieser Abhandlung und ist in „konformer Übersetzung“ aus der Lateinischen Version des 12. Jahrhunderts (der beste Zeuge für den Originaltext) wiedergegeben.
