In a lecture delivered to the British Institute of Philosophy on 15 November 1932, Sir Arthur Eddington wrote in surprisingly modern terms of the problem of merging quantum theory and the general theory of relativity:
At present theoretical physics is divided into macroscopic theory and microscopic theory, the former dealing with systems on a scale comparable with our gross senses, and the latter dealing with the minute substructure underlying the gross phenomena. Broadly speaking, relativity theory covers macroscopic phenomena and quantum theory the microscopic phenomena. The two theories must ultimately be amalgamated, but at present we have not got much beyond the pourparlers for amalgamation. So the gap exists—not, however, as a gap in the external world, but as a gap in our understanding of it. (Eddington 1933, 30)
This suggests that even as far back as 1932 the problem of quantum gravity already had some historical pedigree (there had been pourparlers, as Eddington puts it). Though in somewhat different terms, given the rapid and radical developments in physics at that time, Eddington himself had been thinking about the problem since at least 1918 (see 6.3.1 below). Yet, in the handful of historical studies of quantum gravity that exist,1 it is claimed that quantum gravity research originated with Léon Rosenfeld’s “pioneering” pair of papers from 1930, forging, as they indeed did, both the canonical and covariant quantizations of the gravitational field—though lip service has at least been paid Albert Einstein’s own early prophetic remarks about the potential conflict between general relativity and quantum theory, in papers of his from 1916 onwards,2 but this is still followed by the claim that nothing was really done about it until Rosenfeld tackled the problem (prompted by Wolfgang Pauli).
However, though the version of quantum theory involved was significantly different (and certainly less systematic and coherent) from the present framework (or frameworks)—stemming from the pivotal 1925–1928 developments that produced quantum mechanics and quantum field theory—there was nonetheless a rich debate about the relationship between (old) quantum theory (and the atomic physics that preceded it)3 and gravity. This interaction is to be expected for two reasons:
1the two frameworks were constructed over much the same period of time, often by the same architects;
2the right-hand side of the Einstein field equations must naturally include (in some way) contributions from the matter best described by the quantum theory.
It is true that this work rarely, if ever, involved consideration of quantum properties of the gravitational field, but this could equally be said of some recent approaches that I am nonetheless perfectly content to label “quantum gravity.”4 When I speak of quantum gravity in this paper, I mean it very liberally to indicate any approach that involves dealing with the problem of the coexistence of quantum systems5 and gravitation.
In some ways, this early work closely mirrors what would come later, and indeed, many of the key notions of the later work—the importance of the Planck scale in demarcating the domain of applicability of classical general relativity, the experimental inaccessibility of quantum gravity, and the potentially radical revision of space-time concepts—were discussed even at this early stage. This must surely have contributed to later work, at least in establishing a mindset for thinking about the amalgamation of quantum and gravity. This work deserves to be discussed under the banner of “quantum gravity” just as much as any that would come later, and any attempt to force quantum gravity into the mould of the quantization of the gravitational field (which is implicit in the Rosenfeld story) misses out on both an important source of later ideas and an important set of ideas in their own right.
In this paper I discuss these early skirmishes into and around the problem of quantum gravity, from their prehistory (close to the creation of general relativity) to the development of wave mechanics and just prior to the Dirac equation—at which point the course of quantum gravity research, quite naturally, radically shifts, and there is an appropriate context for the kind of work carried out by Rosenfeld. These early approaches also offer a very useful probe for investigating several important agendas that were in operation at that time, including a desire to meld the cosmological and microscopic, and to unify both physics and our knowledge of physics via axiomatic foundations. A future task is to consider whether and how these agendas continued to play out in the later developments.
For reasons of space and convenience, I focus heavily on papers appearing in the journal Nature during this period. Though it has a potential to introduce an English bias, it nonetheless gives a good snapshot of the general state of research, since it was common practice to supplement more technical publications (e.g., in Zeitschrift für Physik or the Proceedings of the Royal Society) with a brief note in Nature 6 describing the key findings. Indeed, it perhaps offers a closer glimpse into the state of play since a feature of Nature, especially at that time, is almost a direct personal correspondence between individuals that can be found in its pages, via responses in notes and letters—something that could be easily carried out on account of its weekly publication.
Though quantum gravity is today viewed as a slightly strange problem on the frontiers of physics (no doubt because of its highly theoretical and mathematical nature), in the early days surrounding their creation, a fairly natural dialogue between quantum theory and general relativity took place.7 Again, I am here adopting an enormously liberal characterization of the problem of quantum gravity so as to offer an account as inclusive as possible, thus minimizing the risk of sidelining what may have been important sources of later ideas, Eddington’s pourparlers for amalgamation. Whether any of the approaches I discuss amount to quantum gravity in themselves is of course highly debatable, but then there is no such theory yet.
6.1 The Torch of Unification: Mie, Hilbert, Weyl and Haas
I do not wish to cover the already well-trodden ground of the genesis of quantum mechanics and general relativity.8 However, a number of the initial forays into quantum gravity were in many ways extensions of debates that were conducted before the creation of these theoretical frameworks—hence, I am concerned with the pre-pre-history here. One can also find alternative accounts of gravitation—in particular those based on an electromagnetic ether—persisting well beyond the creation of general relativity. One such approach that was clearly of importance (not least to David Hilbert, Hermann Weyl and Eddington) was that of Gustav Mie. I begin with a brief account of Mie’s approach since it marks an approach to the amalgamation of the central theories of physics, as it was then, on the precipice of radical changes.
In 1912 and 1913, Mie sought to develop a (reductive) unified field theory in which both matter and force could be derived from the electromagnetic field (understood as an emergent property of the ether) alone. The core object was a “world function,” and the derivation of gravity and electromagnetism would proceed from this via the calculus of variations—he was not able to get a fully unified theory of both phenomena: Mie’s theory was based on two scalar potentials. The general thrust of Mie’s program stemmed from his belief in the significance of the new empirical facts about the behavior of atoms that had recently emerged. In 1912 he wrote:
The significance of the recently acquired empirical facts about the nature of the atoms ultimately amounts to something essentially only negative, namely that in the atoms’ interior the laws of mechanics and Maxwell’s equations cannot be valid. But regarding what should replace these equations in order to encompass from a single standpoint the profusion of remarkable facts associated with the notion of quantum of action, and in addition the laws of atomic spectra and so forth, the experimental evidence is silent. In fact, I believe that one must not expect anything like that from experiment alone. Experiment and theory must work hand in hand, and that is not possible as long as the theory has no foundation on which it can be based. Thus it seems to me absolutely necessary for further progress of our understanding to supply a new foundation for the theory of matter. With this work, I have tried in the following to make a start, but in view of the difficulty of the matter one should not right away expect results accessible to experiment. The immediate goals that I set myself are: to explain the existence of the indivisible electron and: to view the actuality of gravitation as in a necessary connection with the existence of matter. I believe one must start with this, for electric and gravitational effects are surely the most direct expression of those forces upon which rests the very existence of matter. It would be senseless to imagine matter whose smallest parts did not possess electric charges, equally senseless however matter without gravitation. Only when the two goals I mentioned are reached will we be able to consider making the connection between the theory and the complex phenomena mentioned above. (Mie 2007, 1554)
It is quite clear here the extent to which, in Mie’s mind, gravitation and electromagnetism, and matter are all manifestations of one and the same stuff—this worldview would spread to Weyl, Hilbert, Eddington and many others. Out of this mixture, Mie expected the phenomenological facts of quantum theory to emerge—this theory might somewhat perversely be viewed as an approach to quantum gravity that predates both general relativity and quantum mechanics. At this time in 1913, there were three other (serious) alternative theories of gravitation, those of Einstein and Marcel Grossmann (the Entwurf theory), Abraham Pais, and Gunnar Nordström. Abraham’s theory was inadequate in several ways, chief amongst these being the incompatibility between the variable light speed adopted by Abraham and his usage of the Lorentz transformations. I will return to Nordström’s theory below, for now I quickly explain how Mie’s theory influenced Hilbert.
Hilbert is not a name usually associated with quantum gravity research, but he figures centrally in several early episodes, some of which played a crucial role in later work (at the time of writing, in fact).9 Hilbert was directly involved in aspects of the birth of general relativity, using his beloved variational principles to derive the field equations. He was led to this approach by a rather indirect route involving a modification of Mie’s electromagnetic theory of matter and force: Hilbert made direct use of Mie’s theory in his derivation of general relativity. This imposed a severe restriction on the form of the theory, since it depended upon a specific matter-source. As Pauli put it in his encyclopedia article on general relativity:
Hilbert’s presentation […] was not quite comfortable for the physicists, because in the first place he axiomatically defined the variational principle, and, which is more important, his equations were expressed not for an arbitrary material system, but were based on Mie’s theory of matter. (Pauli 1921, 211)
Einstein10 famously found Hilbert’s approach “childish” since it did not show a proper awareness of the “pitfalls of the real world”—the reason Einstein adopted a “principle theory” approach was, of course, precisely to avoid such pitfalls (in this case “risky hypotheses about the structure of the electron”). The axiomatic method was therefore not a good basis for physical theorizing, according to Einstein.
Hilbert’s ideas about the foundations of mathematics (and his emerging ideas about the unity of scientific knowledge) was combined with this physical background in his celebrated work on general relativity in 1915. What is interesting about this work for this project is that, like Mie, he quite clearly believed that the physics of gravity would be able to unlock the secrets hidden in atomic processes:
As one sees, the few simple assumptions expressed in Axioms I and II suffice by sensible interpretation for the development of the theory: through them not only are our conceptions of space, time, and motion fundamentally reformulated in the Einsteinian sense, but I am convinced that the most minute, till now hidden processes within the atom will become clarified through the fundamental equations herein exhibited and that it must be possible in general to refer all physical constants back to mathematical constants—just as this leads to the approaching possibility, that out of physics in principle a science similar to geometry will arise: truly, the most glorious fame of the axiomatic method, while here, as we see, the mighty instruments of analysis, namely the calculus of variations and invariant theory, are taken into service. (Hilbert 1915, 407)
Whether it was through interactions with Einstein or Weyl, or self-realization about the magnitude of the task he had set himself, Hilbert was a little more subdued a couple of years later. In 1917, Hilbert spoke on “Axiomatic Thought” to the Swiss Mathematical Society in Zurich. At the root of his talk was a belief in the unity of scientific knowledge, with mathematics as the linchpin holding it all together:
I believe that everything which can be the subject of scientific thought, as soon as it is ripe enough to constitute a theory, falls within the scope of the axiomatic method and thus directly to mathematics. By pursuing ever deeper-lying layers of axioms […] we gain ever deeper insights into the essence of scientific thought itself and we become ever more conscious of the unity of our knowledge. In the name of the axiomatic method, mathematics appears called upon to assume a leading role in all of science. (Hilbert 1918, 156)
Weyl was in attendance at this talk and would adopt a formal approach to the problem of unification of gravitation and electromagnetism (though not quantum theory) that was methodologically similar to Hilbert’s. Weyl generalized Riemannian geometry, adding a principle of calibration or gauge (“eich”) invariance to account for the non-integrability of length transference (over non-infinitesimal distances). Einstein had similar gripes with this approach: in this case, the theory had the absurd consequence that objects taken around different paths having identical origins and termini will, at the point of termination, be found to have different sizes and rates.11
The torch of “unity through axiomatization” was carried on, in a rather different way, by Arthur Haas. Haas was a strong advocate of Hilbertian axiomatization, and in his case, it led him to early speculations about matters related to the problem of quantum gravity. For example, as early as 1919, Haas writes (on the basis of “unification” ideals) that:
Arguably, one of the most important future tasks of the axiomatization of physics is the implementation of quantum theory in the system of the general theory of relativity. (Haas 1919, 749)
Though he does not explicitly name the individual constants associated with the ingredient theories (viz.
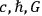 ), it is reasonable to surmise that this is what Haas had in mind in the following passage:
), it is reasonable to surmise that this is what Haas had in mind in the following passage:
The main task of the axiomatization of physics will be the problem concerning the integration of the universal constants of physics. Also the solution of this question may be expected to reveal deeper knowledge of the relations, only intimated by Hilbert, holding between gravity and electricity, and of a further integration of these relations with the quantum hypothesis. (Haas 1919, 750)
This interpretation is somewhat strengthened by the fact that Haas went on to consider the various possible combinations of other constants in other contexts, investigating the way they demarcate domains (Haas 1938). In many ways, this idea that we must consider the integration of the fundamental constants to solve the problem of the relationship between quantum theory and gravitation coincides with the modern understanding.12
6.2 Einstein on the Relationship between Gravity and Quantum
It is a little curious that so many great revolutionary episodes happened almost simultaneously at the beginning of the twentieth century. Perhaps one revolution made it easier for others to follow, via some kind of snowball effect. Whatever the reason, the revolution that resulted in general relativity and the revolution that resulted in quantum theory were close neighbors in time. Einstein was profoundly involved in the creation of both theoretical frameworks, though the former more so than the latter. At the time of the construction of the general theory of relativity, he firmly believed in the existence of quanta of radiation. But this only involved a belief in the property of discreteness (with no real sense of ontological substrate beyond this), rather than belief in what would become quantum mechanics (or quantum field theory—though here too his contributions on emission and absorption of radiation proved crucial). Most physicists believe another revolution is required to bring quantum theory and general relativity together (Rovelli 2000).
Since such quanta, with their discrete energies and other properties, would inevitably couple to the gravitational field (in however small a way), Einstein could not ignore the fact that something would need to be said about the nature of this interaction.13 Even before his article on general relativity had been published in its final form, Einstein was in correspondence with Arnold Sommerfeld about its possible relationship with quantum theory.14 Einstein heard about Sommerfeld’s new theory of spectral lines first-hand while he was still working on general relativity. Sommerfeld thought that the general theory of relativity might be able to offer some help in resolving problems caused by the Stark effect (Sommerfeld 2000, 438). It is quite likely that Sommerfeld’s willingness to consider the relationship between what looked at this stage like disparate fields of inquiry was grounded in a similar belief system to that of Hilbert and Haas (and the Göttingen school), though with a far more empirical basis. Indeed, Silvan Schweber (2009, 269–278) notes that a “doctrine of pre-established harmony” (between mathematics and physics and mathematics and nature) can be found running through much of Sommerfeld’s earlier work. Given this, it is reasonable to expect some inner unity holding between so fundamental a pair of frameworks as relativity and atomic theory.15
Almost as soon as general relativity was completed, Einstein became aware of a possible conflict between it (or, more specifically, the existence of gravitational waves) and the principles of quantum theory,16 and, therefore, the need to say something about the problem of quantum gravity. Thus, he writes that:
[A]s a result of the internal-atomic movement of electrons, atoms must radiate not only electromagnetic but also gravitational energy, if only in minuscule amounts. Since this cannot be the case in nature, then it appears that the quantum theory must modify not only Maxwellian electrodynamics but also the new theory of gravitation. (Einstein 1916b, 696)
In this case, Einstein is clearly aware of the potential clash between the theoretically predicted gravitational radiation combined with the empirically observable stability of atoms: any moving mass (even the electrons in atoms) will radiate gravitational energy (given the right kind of motion, that is).17 In other words, something like Planck’s law of radiation would have to be found for gravitation to account for the stability. He repeated this claim again in 1918, stating that “an improved version of quantum theory would lead to changes in the gravitational theory” (Einstein 1918, 167).
This looks like a potential empirical motivation for pursuing quantum gravity. However, as Gorelik correctly points out, whilst atomic radiation (computed along the lines of James Clerk Maxwell’s theory) leads to the collapse of the atom in
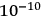 seconds (a fact inconsistent with observations), atomic gravitational radiation, computed using Einstein’s formula, has a collapse time of the order of
seconds (a fact inconsistent with observations), atomic gravitational radiation, computed using Einstein’s formula, has a collapse time of the order of
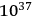 seconds. Therefore, there would in fact be no empirical inconsistency as a result of gravitational radiation, and we should not be puzzled by the stability of atoms in this case.
seconds. Therefore, there would in fact be no empirical inconsistency as a result of gravitational radiation, and we should not be puzzled by the stability of atoms in this case.
Gorelik (1992, 365) argues that an “analogy with electrodynamics” lay behind this comment of Einstein’s. This analogy was a persistent feature of early research on quantum gravity. One must also bear in mind that the issue of absorption and emission of radiation must have occupied a central place in his thinking at the time of writing, for his paper on the emission and absorption of radiation in quantum theory appeared very shortly afterwards—replete with the statement that “it does not seem to be doubtful that the basic idea of quantum theory must be maintained” (Einstein 1916a, 318). What is remarkable, given what we know of the certainty he professed about general relativity, is that he openly considered the possibility that the quantum theory would demand some kind of “modification” of general relativity!18
Quantum theory was invoked several times (in discussions of general relativity and unified field theories) to mark some kind of boundary of the applicability of a theory.19 Einstein himself expressed just this view in a lecture entitled “Ether and the Theory of Relativity” at the University of Leyden in October 1920. This address is interesting for many reasons, historical and philosophical. For our purposes, it is interesting because Einstein once again speculates on the possible restrictions that the quantum theory might place on general relativity:
Further, in contemplating the immediate future of theoretical physics we ought not unconditionally to reject the possibility that the facts comprised in the quantum theory may set bounds to the field theory beyond which it cannot pass. (Einstein 2002, 323)
Indeed, we can find several examples of Einstein expressing this kind of sentiment. Inasmuch as his comments (here and in his 1916 paper) have been investigated by historians, it has tended to be in the context of the study of gravitational waves. It is true that gravitational waves are naturally involved here, but since Einstein is considering the possibility that the radiation of such waves is quantized, we ultimately have what can also be seen as heralding the beginning of research investigating the possible quantization of gravity.
6.3 Quantum Meets Gravity in the Pages of Nature
The pages of Nature, in the period immediately following the construction of general relativity, were littered with a variety of suggestions involving some kind of connection between gravitation and quantum phenomena.20 For example, the period following the well-publicized 1919 observation to test Einstein’s predicted value for the amount of deflection of starlight by the Sun resulted in a steady flow of papers probing the possible relationship between quantum theory and general relativity. This is a fairly natural line of inquiry given the context, since by this time light was, of course, understood in quantum theoretic terms and since gravity was having a direct effect on the propagation of light, it follows that there must be some relation between gravitation and quantum systems. Also the atomic theory of matter based on quantum theory was becoming established, which further deepened the need to consider the connection between gravity and matter in this form.
This episode is of wider historical interest since in many cases the articles were part of their authors’ wider agenda, be it the unity of nature, a distaste for relativity, adherence to the axiomatization program, or some other underlying motivation. Indeed, what is striking about the issues of Nature in and around our chosen period is that there is seen to be no real division between the sciences, and certainly not between atomic physics and gravitational physics. This paper works in a largely chronological fashion, except where there are thematic links across years.
6.3.1 Eddington on Fundamental Length
Eddington discussed the relationship between gravitation and quantum theory from the period following the creation of general relativity to the end of his life.21 Eddington very frequently refers to quantum theory in the context of gravitation and vice versa. In fact, he began to consider the relationship between gravity and quantum at least a year before the deflection observation. It is highly likely that it was as a result of his (and Einstein’s) work on gravitational waves that he was initially led to think about the problem for, as we have seen, Einstein had already contemplated the potential clash between quantum theory and general relativity as a result of his own work on gravitational radiation. Indeed, there are elements of Eddington’s writing, in discussing the gravitational red shift, as far back as 1916 that suggest an emerging awareness of quantum theory’s relevance: “The vibrations of an atom must be slower in an intense field, so that the lines of the solar spectrum should be displaced slightly to the red as compared with terrestrial spectra” (Eddington 1916, 330).
The second installment of this article (appearing in 1918) shows an even greater appreciation of the relationship. Certainly, one of the more remarkable things that emerges from Eddington’s early work on general relativity is his claim that a fundamental length can be formed from the three basic universal constants, and that this length will inevitably form a piece of the future theory blending quantum and gravity:
From the combination of the fundamental constants,,
, and
it is possible to form a new fundamental unit of length
. It seems to be inevitable that this length must play some role in any complete interpretation of gravitation. […] In recent years great progress has been made in knowledge of the excessively minute; but until we can appreciate details of structure down to the quadrillionth or quintillionth of a centimetre, the most sublime of all the forces of Nature remains outside the purview of the theories of physics. (Eddington 1918, 36)
This is a remarkably prescient passage; though it appears somewhat clumsily disconnected from the rest of the article appearing as the final paragraph. In it Eddington has clearly targeted what we now label “the Planck length,”
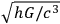 .22
This length is, of course, a fairly generic feature of all modern approaches to quantum gravity.23
That Eddington believes this length to inevitably play a role in a future interpretation of gravitation plainly implies that he sees quantum theory as essentially bound up with the physics of gravitation.
.22
This length is, of course, a fairly generic feature of all modern approaches to quantum gravity.23
That Eddington believes this length to inevitably play a role in a future interpretation of gravitation plainly implies that he sees quantum theory as essentially bound up with the physics of gravitation.
In the paragraph immediately preceding the above quoted paragraph, Eddington states (again, rather presciently) that:
[W]e know that in consequence of the undulatory theory of light, a ray traversing a heterogeneous medium always takes the path of least time; and one can scarcely resist a vague impression that the course of a material particle may be the ray of an undulation in five dimensions. (Eddington 1918, 36)
Eddington clearly has in mind here a notion of the particle as a “projection” of a wave phenomenon down from five to four dimensions (as in the later more well-known Kaluza-Klein theories). One might immediately latch upon the work of Gunnar Nordström (1914) as a precedent for such five-dimensional speculations; though Nordström’s theory was based on a scalar theory of gravitation. However, given Nordström’s isolation it is highly likely that Eddington was not aware of his paper.24 Although it is quite likely that Eddington’s off-hand remark might have sparked higher-dimensional thoughts in Theodore Kaluza and others.
Joseph Larmor, in discussing the possible application of quaternions to general relativity, suggests something strikingly similar (again independently, it seems, of Nordström and Kaluza),25 and in a way that makes projective notions more explicit. He labels it a “hyperspacial version of the Einstein gravitational theory” (Larmor 1919b, 357). Larmor initially develops a symbolic geometrical calculus (devised by W. J. Johnston) to talk about electromagnetism in flat space-time (i.e., with
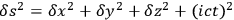 ). However, he is concerned with introducing gravitation into his scheme, and notes that this can be achieved by introducing a new dimension
). However, he is concerned with introducing gravitation into his scheme, and notes that this can be achieved by introducing a new dimension
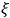 (“preferably of space” (Larmor 1919b, 353)), such that
(“preferably of space” (Larmor 1919b, 353)), such that
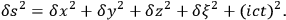
|
6.1 |
Since this includes electromagnetism too, an additional component is received by the vector potential. The idea is to have the physics of flat four-dimensional space-time “as a hypersurface within our auxiliary flat five-dimensional scheme, in which both the electrodynamic and the gravitational theory shall exist.” He develops this idea as follows:
Now any continuum of four dimensions, having a quadratic line-element, however complex, is expressible as a hypersurface in this homaloid continuum of five dimensions. If these considerations are correct, the Einstein generalisation, made with a view to include gravitation within his four dimensions, must be interpretable as the geometry of some type of hypersurface constructed in this extended homaloid of five dimensions. For the previous homaloid theory of Minkowski which ignored gravitation, this hypersurface, existing in the five dimensions, in which the world-process is represented, is flat; or more conveniently in some connections it may be taken as a closed region (hypersphere) of assigned uniform extremely small curvature, instead of the unlimited hyperplane. The problem then is to include in the scheme the influence—actually very slight in realizable cases—of gravitation; and this is to be done by recognising slight local deformations on this hypersphere in order to represent that effect. Now in the four-dimensional Minkowski map of the historical world-process, the rays of radiation are the curves of minimum length on the locus for which the analytic element of lengthvanishes; and the paths of particles when gravitation was neglected were the curves (then straight lines in the flat) for which the length between assigned terminal points is minimum. If the hypersurface, which is very nearly uniform of very small curvature in the actual problem as presented in nature, can be so chosen that these two relations persist—namely, that the rays of light shall be geodesics on the locus determined by
vanishing, and the free orbits of particles with gravitation now introduced shall be the paths of minimum length on the hypersurface—then one way of absorbing the universal phenomena of gravitation, into the mixed space-time scheme which has arisen from and has transcended and obliterated the previous idea of relativity of positions and motions, will have been accomplished.26 (Larmor 1919b, 354)
Larmor associates this idea of generalizing dimensions (and dealing with the properties of one as projections in another) with Clifford. These several proposals for “dimensional expansion” indicate that when Kaluza formulated his five-dimensional formulation of gravitation and electromagnetism, he did so in a period when such speculations were not entirely rare. Of course, this idea of increasing the number of space-time dimensions is a central feature of string theoretic approaches to quantum gravity.
6.3.2 Larmor’s Paradox
In the Christmas Day edition of Nature in 1919, Larmor drew attention to a potential conflict (a paradox, in fact)27 between the quantum theory of light and the manner in which light is treated in general relativity, to raise doubts about the veracity of the latter. As Larmor saw it (Larmor 1919a, 516), Einstein’s general theory demands on the one hand (given an undulatory description of light) that the velocity of light will be diminished as it nears the Sun, but that “the scale of time” must undergo a compensatory expansion so that, overall, there is no change in wavelength. Larmor refers to such a notion of time as “heterogeneous time” and argues that given this notion (and given that space is almost flat), the path of a ray of light will be determined “fundamentally by minimum number of wave, and not by minimum time” (Larmor 1919a, 516). In this case, claims Larmor, there ought (on kinematical grounds) to be no such deflection of light passing the Sun.
However, Larmor then considers a dynamical explanation for the deflection test, drawing in Einstein’s work on the quantum theory of light. According to this description, the velocity of light ought to increase, and according to Einstein’s theory, in just the amount observed:
Dr. Einstein requires in another connection that light should consist of discrete bundles or quanta of energy. Let it also be granted that inertia and gravitation are attributes of energy. It seems to follow that each of these bundles of energy will swing round the Sun in a hyperbolic orbit, and that its velocity will be increased when near the Sun. It is well known that this would account for half the observed deflection. But, again, physical optics could not exist without the idea of transverse waves and their phases, which must be grafted on somehow to the bundles of energy. (Larmor 1919a, 412)
Larmor can be seen to be clearly grappling with the puzzling “wave-particle” nature of light, and seizes upon the opportunity of applying this puzzle to general relativity to render it less certain. Given this conflict, he argues that the recent deflection test conducted by Eddington should be looked upon as a “guide rather than a verification” (Larmor 1919a, 412). Of course, Einstein’s own path would involve an engagement with just such issues. His approach was to consider the quantum, particulate aspects as merely an emergent phenomenon (as special solutions) from an underlying classical field theory. He had, moreover, already (by this stage) considered the possibility of a “quantum correction” to general relativity.
6.3.3 The Cavendish Lab’s Intervention: Radioactivity and Gravitation
An experimental venture into the interaction of the gravitational field with what were slowly becoming viewed as quantum properties of particles was conducted by Ernest Rutherford and Arthur Compton at the Cavendish Laboratory. It appeared in the same Christmas Day issue as Larmor’s article discussed above. Their paper constituted a response to an article by Prof. Donnan from the previous week’s issue over the behavior of radioactive substances in strong gravitational fields.28 They note that pretty much the same question was put to them by “Dr. Schuster” some years earlier. The problem considered was whether the intensity of gravitational field strength could modify the rate of transformation of various radioactive substances. Before they had a chance to put Arthur Schuster’s question to the test,29 the First World War intervened.
Rutherford and Compton (1919) bypass the need to use a large heterogeneous mass to generate a suitable gravitational field by using the equivalence between gravitational acceleration and centrifugal acceleration. They therefore performed the experiment by placing radioactive substances at the edge of a rapidly spinning disc (generating 20,000 times the strength of the Earth’s gravitational field) and measured
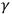 -ray rate responses (using a balance method), looking for (significant) discrepancies. However, as they noted, on the basis of Donnan’s calculations, no change in rate was to be expected since, if it existed, the effect would be “very much smaller than can be detected by measurements of this character” (Rutherford and Compton 1919, 412).30
-ray rate responses (using a balance method), looking for (significant) discrepancies. However, as they noted, on the basis of Donnan’s calculations, no change in rate was to be expected since, if it existed, the effect would be “very much smaller than can be detected by measurements of this character” (Rutherford and Compton 1919, 412).30
Note that their method followed Einstein’s own suggestion, in his “popular account” of relativity, from 1916 (Einstein 1997). He considers a setup in which a clock is situated on a spinning disc, a certain distance
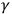 from the center. The clock’s velocity, relative to a frame
from the center. The clock’s velocity, relative to a frame
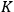 at rest with respect to the moving clock, is
at rest with respect to the moving clock, is
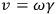 (where
(where
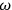 is the angular velocity). Where
is the angular velocity). Where
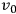 represents the “number of ticks of the clock per unit time […] relative to
represents the “number of ticks of the clock per unit time […] relative to
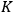 when the clock is at rest,” (Einstein 1997, 388) the rate of the clock when it is moving relative to
when the clock is at rest,” (Einstein 1997, 388) the rate of the clock when it is moving relative to
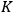 with velocity
with velocity
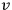 (but at rest relative to the disc) is:
(but at rest relative to the disc) is:
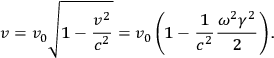
|
6.2 |
He then considers the difference of potential of the centrifugal force between the clock’s position and the disc’s center, written
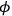 :
:
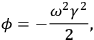
|
6.3 |
which, on substitution into eq. (6.2) gives:
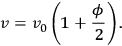
|
6.4 |
From which one derives the time dilation as a result of the centrifugal acceleration. The equivalence principle leads one to the result that observers rotating with the disc will find themselves in a gravitational field with potential
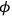 . This is then applied to an atom that is emitting spectral lines, which can be viewed by analogy with the clock. The expectation will then be that:
. This is then applied to an atom that is emitting spectral lines, which can be viewed by analogy with the clock. The expectation will then be that:
An atom absorbs or emits light of a frequency which is dependent on the potential of the gravitational field in which it is situated. (Einstein 1997, 389, italics in the original)
But after considering a centrifugal (acceleration) example, Einstein then switches (for obvious practical reasons) to consideration of an atom on the surface of a heavenly body, noting that its frequency will be a little less than the frequency of the same element on a smaller, less massive body. One could test this with spectral lines originating on the Sun and the Earth, respectively. Though there is no Planck’s constant in this example, and so this is not by any means a quantum gravitational phenomenon, at root this is about something (spectral lines) that was central in discussions of the old quantum theory. In intervening in atomic frequencies, the gravitational field was surely intervening in quantum processes.
There were, then, some early experimental suggestions concerning the influence of gravity on elementary processes, but these quickly died out. It is possible that this was due to Eddington’s theoretical calculations and these null results from the Cavendish Lab.31 However, it was, of course, already known that the gravitational effects on single atoms would be miniscule simply by inspecting the size of the gravitational constant. In this sense, the Cavendish Lab’s results merely confirmed what was already believed.32
Before I leave this section, I note that it seems that the debate discussed here was in many ways a direct continuation of an earlier one on the relationship between gravitation and temperature following experiment work by Philip E. Shaw (1916). This work stretches back to a period before general relativity was established and that remained largely independent of general relativity even when it did become better established. Shaw had conducted experiments in 1915, with a Cavendish torsion balance. These pointed to a positive temperature coefficient for the gravitational constant. Shaw’s theoretical position was roundly criticized, not least by Oliver Lodge (1916; 1917), who pointed to several problems with momentum non-conservation and potential empirical inadequacies. However, Shaw’s experimental work was positively received, and it was this that filtered through into the later work on the relationship between radioactivity and gravitation.
6.3.4 Einstein on the Development of Relativity
In 1921, following an outline of how he arrived at the form of general relativity, Einstein concluded his account with a list of:
[…] important questions which are awaiting solution […]. Are electrical and gravitational fields really so different in character that there is no formal unit to which they can be reduced? Do gravitational fields play a part in the constitution of matter, and is the continuum within the atomic nucleus to be regarded as appreciably non-Euclidean? (Einstein 1921, 784)
As I understand it, here Einstein is, firstly, hinting at a unified field theory, through which both gravitational and electrical forces are described. On the basis of this, the question is begged as to whether gravitational force plays any role in holding atoms together.33 Finally, and most interesting, it is natural to consider what kind of gravitational field would exist in the interior of an atom—though Einstein thinks directly in terms of what space-time would look like inside atoms. This has a bearing on the other questions since, unless the space-time is appreciably curved, there will be no work for gravitation to do in the structure of matter. What can be reasonably inferred from this is that Einstein was considering the possibility that general relativity might have something to say about the constitution of matter, and a fortiori the nature of quantum theory. This is backed up by remarks that Einstein is reported to have made following a lecture at King’s College London in 1921:
After the public lecture Prof. Einstein was the guest of the Principal […]. In responding to his health, Prof. Einstein made an interesting revelation of his attitude to the quantum theory. This theory was, he said, presenting a difficult problem to physics, but the very nature of the difficulty served to bring into relief the attractiveness and satisfaction of the principle of relativity. That principle had served to give a simple and complete explanation of experimental facts which under any other aspect were discordant. In the quantum theory as it stood at present we were faced with discordant experimental facts, and were searching for the principle on which to interpret them. (Anonymous 1921, 504)
One inference to make here is that Einstein expected that the general theory of relativity itself might be able to supply such a missing principle on which to found a satisfactory theory of matter, quantum or not. However, Sauer, in a private email to the author on 15 September 2011, interpreted the passage as more likely indicating that Einstein had in mind, not that the principle of relativity would itself serve as a guide for quantum theory, but rather that something analogous to the principle of relativity, though of a different sort, more relevant for quantum theory (such as the correspondence principle or the adiabatic principle), might be required to interpret the experimental data then available. However, given that, at this time, Einstein considered the direct role of gravitation in the constitution of matter one of his most important questions in need of resolution, it is perfectly possible that he intended what I suggest.
6.3.5 Jeans on Indeterminism in GR and QM
In 1926, James Jeans presented a curious argument suggesting that the “unpalatable determinism” brought forth by relativity (in the form of the “block universe”) might be somehow cured by developments in quantum theory. To modern ears, this might sound the wrong way around, since it is the indeterminism of quantum theory that is unpalatable to many.
It is clear that Jeans has in mind fatalism here, since he writes that “Einstein’s work on relativity changed the universe from a drama into a picture drama” (Jeans 1926, 311). Clearly he supposed that the random nature of atomic processes could inject some much-needed randomness into all processes:
[R]elativity is not the whole of natural science; it is not even the whole of Einstein’s work. His contributions to science fall into two columns which, unhappily, are parallel and show no signs of meeting. The first column contains his contributions to the theory of relativity, […] the second column contains his contributions to the theory of quanta […]. It is not yet altogether clear which of these columns will figure most prominently in the history of present-day science when this is finally written in its proper perspective. But it already seems possible that the second column of Einstein’s work may contain the needed antidote to the determinism and automatism to which the first column, if it stood by itself, would seem to condemn us. (Jeans 1926, 311)
Jeans is clearly well aware of the problem of bringing together quantum and gravity—that is, of the task of saying something about the “meeting” between the “two columns”—however, the probabilistic nature of quantum theory was still not fully appreciated by the wider scientific community,34 nor were the dynamics of general relativity (qua theory describing the evolution of geometrical data) understood. Indeed, Jeans apparently viewed the four-dimensional nature of Einstein’s theory as its core distinguishing feature. Or, as he puts it, “the dynamical explanation of a gravitational force crumbled in the hands of Einstein” (Jeans 1926, 311). However dated Jeans’s specific comments may strike us now, they mark a very clear expression of the problem of quantum gravity as a potential conceptual (rather than “merely technical”) clash. It is also an early example of a proposal to utilize one of the ingredient theories of quantum gravity to resolve some supposed problem with the other. In this case, it was the conceptual problem of the block-like nature of the universe according to general relativity, and Jeans proposed that the theory of quanta might offer some assistance in changing the worldview “back into a drama.”
6.3.6 Klein on Five-dimensional Quantum Relativity
Oskar Klein came up with the idea of a five-dimensional approach while visiting Ann Arbor as an instructor in theoretical physics at the University of Michigan. Klein began working on the approach in 1924, then returned to this initial foray when he returned to Copenhagen in 1925. He published a paper in Nature a little after the more well-known paper from Zeitschrift für Physik, though both appeared in 1926. It was Pauli who, early in 1926, informed Klein that Kaluza had already published on a similar idea (Pais 2000, 131). However, there is genuine novelty in Klein’s approach in that Planck’s constant emerges as a consequence of topological structure. Or, as Klein puts it, his result “suggests that the origin of Planck’s quantum may be sought just in this periodicity in the fifth dimension” (Klein 1926b, 516).
This was a new development of the much older idea that geometry and topology could be used as a “resource” in world-building. In fact, in his later recollections of how he came to the five-dimensional idea, Klein describes an approach broadly similar to that envisaged by Larmor and, earlier, Eddington (as described above). He notes how he was searching for “a wave background to the quantization rules” and had been playing with:
[T]he idea that waves representing the motion of a free particle had to be propagated with a constant velocity, in analogy to light waves—but in a space of four dimensions—so that the motion we observe is a projection on our ordinary three-dimensional space of what is really taking place in four-dimensional space. (Klein 1991, 108–109)35
Klein was in discussions with Paul Ehrenfest and George Eugene Uhlenbeck in the spring of 1926, during a visit to Leiden at Ehrenfest’s invitation, and the discussions were enough to lead to a paper on five-dimensional relativity by Ehrenfest and Uhlenbeck (1926), appearing around the same time as Klein’s own note in Nature (Ford 2009, 9–10).36 Ehrenfest had a long fascination with the concept of dimensionality. Long before Klein began thinking about his dimensional expansion, Ehrenfest (1917) had written on the possible reasons why space is three-dimensional, showing how various processes and the stability of orbits depend on it. This might well have been behind Klein’s own suggestion, given that physical quantities would be periodic functions of the compact dimension and observables would be given as averages over the small circumference, that ordinary space must be three-dimensional (Klein 1991, 110).
As with several other approaches mentioned in this paper, Klein’s work on five-dimensional relativity might be seen to fall somewhat outside of the category of quantum gravity. However, as with many of the other approaches discussed, the influence of the work on later quantum gravity research cannot be underestimated. Further, it shows how, in some sense, the shape of space (a feature dynamically determined within general relativity) can determine what would be otherwise inexplicable features of the world (in this case the existence of a quantum of action). Of course, it was already known following general relativity that geometry offers a potentially exceptional explanatory resource, but Klein’s work showed that this resource was more widely applicable than previously supposed.
As mentioned above, Klein’s approach was closely related to the earlier efforts of Kaluza (1997), and Klein begins by outlining Kaluza’s approach. Kaluza himself was inspired by Weyl’s earlier modification of the metric of general relativity, so as to have a total metric that could account for (what was then) “all physical phenomena” (Kaluza 1997, 53). The introduction of a space-time fifth dimension was necessary in such a theory since in four dimensions the only Christoffel symbols that are available are those of the gravitational field. Kaluza imposed a “cylinder condition,” effectively eliminating variations with respect to the fifth dimension by regarding
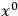 derivatives as having very small or zero magnitudes.
derivatives as having very small or zero magnitudes.
Though Kaluza’s approach was purely classical, he does conclude his 1921 article with a consideration of its microscopic significance:
[M]atter, in its fundamental constituents at least, is not weakly charged; in the words of H. Weyl its ‘macroscopic placidity’ stands in sharp contrast to its ‘microscopic turbulence’, and this is true in particular for the new coordinate: for the electron or H-nucleus the quantity
[the ratio of charge density to rest-mass density, or the “specific charge” of matter] and with it the “velocity”-component is anything but small! In the form demanded by Approximation II [very small specific charge] the theory can describe at most macroscopic phenomena and the key question is whether it can be used for the above elementary particles.
If one tries to describe the motion of electrons by geodesics inone encounters immediately a difficulty that threatens to destroy the whole structure. The problem is that, if one takes the earlier assumptions literally, the fact that
(in lightseconds) means that the quantity
is so large that the last term in [
]37, instead of disappearing, takes a value much greater than is observed experimentally and becomes the leading term. […] [I]t would seem to be impossible to proceed in the old manner without some new hypotheses. (Kaluza 1997, 57)
Kaluza’s solution to the problem was to throw out the gravitational constant “so that gravitation would appear as a sort of difference-effect” (Kaluza 1997, 57). This, Kaluza argues, would have as an “attractive feature,” the fact that a “statistical role” could be attributed to the gravitational constant. He finishes by remarking that “for the moment the consequences of this hypothesis cannot be foreseen; and of course there are other possibilities to consider. And threatening all universal hypotheses is the Sphinx of modern physics, the quantum theory” (Kaluza 1997, 58).
Klein focuses directly on Kaluza’s “Sphinx”, on the microscopic description. He also diverges from Kaluza in assigning a definite scale to his
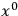 and treating it realistically. The approach involves the establishment of a link between Kaluza’s unified theory and the (then) brand new work on quantum mechanics of Louis de Broglie and Erwin Schrödinger. He characterizes Kaluza’s approach as a unified theory in which the unification is achieved via the coefficients
and treating it realistically. The approach involves the establishment of a link between Kaluza’s unified theory and the (then) brand new work on quantum mechanics of Louis de Broglie and Erwin Schrödinger. He characterizes Kaluza’s approach as a unified theory in which the unification is achieved via the coefficients
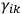 of the five-dimensional Riemannian line-element mentioned in footnote 37. Klein shows how one can view the equations of motion for charged particles propagating in an electromagnetic field (constructed by Kaluza) as radiation equations (that is, according to which matter is a wave phenomenon). When this viewpoint is adopted, a generalization of the wave equation follows. Restricting to a class of solutions in which the fifth dimension has a period related to Planck’s constant, then, Klein argues, the standard quantum mechanical laws drop out. Hence, one has a unified theory of electricity and magnetism, and one has an elementary notion of quantum theory that appears as a consequence of the theory. In a sense we find in Klein’s approach geometry being used as a resource in the construction, deduction, or explanation of other puzzling phenomena.
of the five-dimensional Riemannian line-element mentioned in footnote 37. Klein shows how one can view the equations of motion for charged particles propagating in an electromagnetic field (constructed by Kaluza) as radiation equations (that is, according to which matter is a wave phenomenon). When this viewpoint is adopted, a generalization of the wave equation follows. Restricting to a class of solutions in which the fifth dimension has a period related to Planck’s constant, then, Klein argues, the standard quantum mechanical laws drop out. Hence, one has a unified theory of electricity and magnetism, and one has an elementary notion of quantum theory that appears as a consequence of the theory. In a sense we find in Klein’s approach geometry being used as a resource in the construction, deduction, or explanation of other puzzling phenomena.
6.4 On the Way to Quantum Geometry
The relationship of gravity (and indeed general relativity) to the phenomena revealed by quantum theory was used strategically by those who opposed relativity around the 1920s. Lodge, for example, thought that “if posterity is forced to accept and employ devices […] for dispensing with the ether I fear that a damaging blow will have been dealt at physics” (Lodge 1919, 62).
However, Lodge signaled an early warning for those who might wish to link the discontinuity of matter with space-time:
May I parenthetically urge philosophers to be on their guard against any system which introduces discontinuity into space or time, or even energy? Matter is discontinuous, electricity is discontinuous, I venture to say that real number is discontinuous; but space and time and ether are continuous. Energy may acquire a discontinuous aspect in its relation with matter, and the quantum is an important metrical fact, but it is explicable in terms of the atom or electron, and is not a feature in energy itself. Time is absolutely continuous, however it be measured and expressed numerically. (Lodge 1919, 62)
Developments from as early as the 1930s—that have persisted to the present day, packaged in the concept of “quantum geometry”—would follow just the path attacked by Lodge, himself too strongly committed to classical physics and the ether theory to budge.
An even earlier statement of potential short-distance gravitational distortions was given in an editorial of 1919:
If the distortion of space were very great, the customary methods of dynamics might lose their significance; and the question arises: Will, on Einstein’s theory, the space inside an atom be so far from Euclidean that ordinary dynamical methods are unjustifiable? The answer to this question is “No.” There are two lengths which have special significance in connection with the atom; one of these is what we call the radius of the atom, and is of the ordercm; the other we call the radius of the electron, and is about
cm. Even at the smaller of these distances the gravitational potential due to the mass of the atom, and therefore the distortion from Euclidean space, would be exceedingly small compared with the corresponding quantities due to Earth at its surface, so that there is no special distortion inside the atom, except at distances from the centre which are infinitesimal even when compared with the radius of an electron. (Lodge 1921a, 354)
Not unrelated is the suggestion made by Norman Campbell in 1921, arguing that better sense could be made of the interior of atoms if the distinction between stationary and moving electrons were abolished by arguing that time ceased to make sense in the interior of atoms:38
The suggestion that I made is that, by means of a generalized principle of correspondence, the distinction between moving and fixed electrons might be abolished and the conceptions that have proved so fruitful in explaining spectra made available immediately for explaining also such things (if there are such things) as are only explicable by fixed electrons. Thus the distinction would be abolished if ‘time’ had no meaning inside the atom. For the difference between electrons following an orbit and electrons fixed at points on that orbit can only be expressed in terms of temporal conceptions; if all such conceptions are totally invalid in dealing with problems of atomic structure the distinction vanishes. (Campbell 1921, 170)
One wonders whether such suggestions could have been conceptualized in this way were it not for the parallel debates in the context of general relativity.
The gravitational field of the electron (though classically conceived) received an interesting early speculative treatment by George Jeffrey (1921). As with many other papers already discussed, Lodge (1921b) thought fit to comment on this paper of Jeffrey’s in Nature. The aim of Jeffrey’s paper was to show how the gravitational field might be involved in the structure of the electron, with the conclusion that the electrical and mass potentials offer some kind of stabilizing effect by opposing each other. Again, Lodge translates the “ether-free” discussion into one concerning the state of the ether close to an electron.
The introduction by Uhlenbeck and Samuel Goudsmit (1926) of the hypothesis of quantized angular momentum of electrons (to explain several puzzling results in quantum theory and experiment) radically altered the landscape, both for quantum theory and for the kinds of models needed in general relativity. Eddington (1926) discusses a potential conflict between the spinning electron hypothesis and relativity theory. He notes that some have been perplexed by what seems like a straightforward conflict between relativity’s prohibition of superluminal velocities and the fact that the electron’s periphery apparently moves at just such velocities. Eddington dissolves the perplexity in two ways: firstly, the prohibition applies to the propagation of signals, but clearly no such signaling is possible by utilizing the electron’s angular velocity. Secondly, the spin is a quantum number: it represents, as Eddington says, “a state of the world” (Eddington 1926, 652). Finally, he notes that the idea that the electron has a space-like (superluminal)
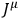 vector was already postulated by Weyl in connection with his investigation into the relationship between gravitational and electrical fields, and was deduced purely from his action-principle. Again, this clearly points to the fact that the domains of the large and small, gravitational and atomic, were not seen to be disconnected. The view that the world of the quantum and of gravity is a schizophrenic one came with later (failed) attempts to directly quantize general relativity.39
vector was already postulated by Weyl in connection with his investigation into the relationship between gravitational and electrical fields, and was deduced purely from his action-principle. Again, this clearly points to the fact that the domains of the large and small, gravitational and atomic, were not seen to be disconnected. The view that the world of the quantum and of gravity is a schizophrenic one came with later (failed) attempts to directly quantize general relativity.39
6.5 Conclusion
In this paper I have examined the very earliest work on the problem of quantum gravity (understood very liberally). There was a very lively debate in this early stage, and no suggestion that such a theory would not be forthcoming. Indeed, there are, rather, many suggestions explicitly advocating that an integration of quantum theory and general relativity (or gravitation, at least) is essential for future physics, to construct a satisfactory foundation. I have also demonstrated how this belief was guided by a diverse family of underlying agendas and constraints, often of a highly philosophical nature. A subsequent paper will trace the fate of these agendas as quantum theory was put on a firmer footing.
Abbreviations and Archives
| Niels Bohr Library & Archives | American Institute of Physics, College Park, MD, USA, http://www.aip.org/history/ohilist/4922_5.html |
Acknowledgements
I would like to thank Shaul Katzir and Tilman Sauer for their helpful comments on an earlier draft. I would also like to thank the Australian Research Council for their support via the Discovery Project Grant DP0984930.
References
Anonymous (1921). Prof. Einstein's Lectures at King's College London, and the University of Manchester. Nature 107(2694): 504
Ashtekar, Abhay (2005). The Winding Road to Quantum Gravity. Current Science 89: 2064-2075
Buchwald, Diana, Tilman Sauer, T. S., Rosenkranz Tilman, R. T. (2006). The Collected Papers of Albert Einstein. Volume 10. The Berlin Years. Princeton: Princeton University Press.
Campbell, Norman (1921). Atomic Structure. Nature 107(2684): 170
Corry, Leo (1997). David Hilbert and the Axiomatization of Physics (1894–1905). Archive for History of Exact Sciences 51: 83-198
- (1999). From Mie's Electromagnetic Theory of Matter to Hilbert's Unified Foundations of Physics. Studies in History and Philosophy of Modern Physics 30(2): 159-183
DeWitt, Bryce S. (1967). Quantum Theory of Gravity I. The Canonical Theory. Physical Review 160(5): 1113-1148
Donnan, Frederick G. (1919). Heat of Reaction and Gravitational Field. Nature 104(2616): 392-393
Durham, Ian T. (2003). Eddington and Uncertainty. Physics in Perspective 5: 398-418
Earman, John, Clark Glymour (1978). Einstein and Hilbert: Two Months in the History of General Relativity. Archive for History of Exact Sciences 19: 291-308
Eddington, Arthur S. (1916). Gravitation and the Principle of Relativity I. Nature 98(2461): 328-330
- (1918). Gravitation and the Principle of Relativity II. Nature 101(2524): 34-36
- (1926). Spinning Electrons. Nature 117(2949): 652
- (1933). Physics and Philosophy. Philosophy 8: 30-43
- (1949). Fundamental Theory. Cambridge: Cambridge University Press.
Ehrenfest, Paul (1917). In What Way Does It Become Manifest in the Fundamental Laws of Physics that Space Has Three Dimensions?. Proceedings of the Amsterdam Academy 20: 200-209
Ehrenfest, Paul, George Uhlenbeck (1926). Graphische Veranschaulichung der De Broglieschen Phasenwellen in der fünfdimensionalen Welt von O. Klein. Zeitschrift für Physik 37: 895-906
Einstein, Albert (1916a). Strahlungs-Emission und Absorption nach der Quantentheorie. Verhandlungen der Deutschen Physikalischen Gesellschaft 18: 318-323
- (1916b). Näherungsweise Integration der Feldgleichungen der Gravitation. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin XXXII: 688-696
- (1918). Über Gravitationswellen. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin
- (1921). A Brief Outline of the Development of the Theory of Relativity. Nature 106(2677): 782-784
- (1997). On the Special and General Theory of Relativity (A Popular Account). In: The Collected Papers of Albert Einstein. Volume 6. The Berlin Years: Writings, 1914–1917 Ed. by Anne J. Kox, Martin J. Klein, M.J. K.. Princeton: Princeton University Press 247-420
- (2002). Ether and the Theory of Relativity. In: The Collected Papers of Albert Einstein. Volume 7. The Berlin Years: Writings, 1918–1921 Ed. by Michel Janssen, Robert Schulmann, R. S., Illy Robert, I. R.. Princeton: Princeton University Press 305-323
Ford, George (2009). George Eugene Uhlenbeck, 1900–1988: A Biographical Memoir. Washington, D.C.: National Academy of Sciences.
Freed, Simon, Arthur H. Jaffey, A.H. J. (1942). High Centrifugal Field and Radioactive Decay. Physical Review 63: 12-17
Galison, Peter L., Michael Gordin, M. G. (2001). Quantum Mechanics: History of Modern Physical Science. New York: Routledge.
Gillies, George T., C. S. Unnikrishnan (2002a). Experimental Perspectives on the Interplay of Quantum and Gravity Physics. In: Advances in the Interplay between Quantum and Gravity Physics Ed. by Peter G. Bergmann, Venzo Sabbata. Dordrecht: Kluwer 103-122
- (2002b). Quantum Physics-Motivated Measurements and Interpretation of Newtonian Gravitational Constant. In: Advances in the Interplay between Quantum and Gravity Physics Ed. by Peter G. Bergmann, Venzo Sabbata. Dordrecht: Springer 123-132
Goldstein, Catherine, Jim Ritter (2003). The Varieties of Unity: Sounding Unified Theories 1920–1930. In: Revisiting the Foundations of Relativistic Physics Ed. by Abhay Ashtekar, Robert S. Cohen, R.S. C., Howard Robert S., H. R.S., Don Howard. Dordrecht: Springer 93-149
Gorelik, Gennady (1992). The First Steps of Quantum Gravity and the Planck Values. In: Studies in the History of General Relativity Ed. by Jean Eisenstaedt, Anne J. Kox. Boston: Birkhäuser 364-379
Gupta, Suraj (1962). Quantum Theory of Gravitation. In: Recent Developments in General Relativity Ed. by Leopold Infeld. Oxford: Pergamon Press 251-258
Haas, Arthur (1919). Die Axiomatik der Modernen Physik. Naturwissenschaften 7(41): 744-750
- (1938). The Dimensionless Constants of Physics. Proceedings of the National Academy of Sciences of the United States of America 24(7): 274-276
Hafele, Joseph C., Richard E. Keating (1972). Around-the-World Atomic Clocks: Predicted Relativistic Time Gains. Science 177(4044): 166-168
Halpern, Paul (2004). Nördstrom, Ehrenfest, and the Role of Dimensionality in Physics. Physics in Perspective 6: 390-400
Hilbert, David (1915). The Foundations of Physics (First Communication). In: The Genesis of General Relativity, Volume 4. Gravitation in the Twilight of Classical Physics: The Promise of Mathematics Ed. by Jürgen Renn. Dordrecht: Springer 2007 1003-1015
- (1918). Axiomatisches Denken. Mathematische Annalen 79: 405-415
Hu, Bei-Lok (2009). Emergent/Quantum Gravity: Macro/Micro Structures of Spacetime. Journal of Physics: Conference Series 174: 1-16
Jeans, James (1926). Space, Time, and Universe. Nature 2939(117): 308-311
Jeffrey, George B. (1921). The Field of an Electron on Einstein's Theory of Gravitation. Proceedings of the Royal Society A 99(697): 123-134
Joly, John (1920). Relativity and Radio-Activity. Nature 104(2619): 468
Kaluza, Theodore (1997). Zum Unitätsproblem der Physik. In: The Dawning of Gauge Theory Ed. by Lochlainn O ' Raifeartaigh. Princeton: Princeton University Press 53-58
Kilmister, Clive (1994). Eddington's Search for a Fundamental Theory. Cambridge: Cambridge University Press.
Klein, Oskar (1926a). Quantentheorie und fünfdimensionale Relativitätstheorie. Zeitschrift für Physik A 37(12): 895-906
- (1926b). The Atomicity of Electricity as a Quantum Theory Law. Nature 118: 516
- (1991). From My Life of Physics. In: The Oskar Klein Memorial Lectures Ed. by Gösta Ekspong. Singapore: World Scientific 103-117
Kragh, Helge (2000). Relativity and Quantum Theory from Sommerfeld to Dirac. Annalen der Physik (Leipzig) 9(11–12): 961-974
Larmor, Joseph (1919a). Gravitation and Light. Nature 104(2617): 412
- (1919b). On Generalized Relativity in Connection with Mr. W. J. Johnston's Symbolic Calculus. Proceedings of the Royal Society A 96(678): 334-363
Lodge, Oliver (1916). Gravitation and Temperature. Nature 97(2433): 321
- (1917). Gravitation and Thermodynamics. Nature 99(2475): 104
- (1919). Time, Space, and Material, II. Symposium: Time, Space, and Material: Are They, and If so in What Sense, the Ultimate Data of Science?. Proceedings of the Aristotelian Society, Supplementary Volumes 2: 58-66
- (1921a). Gravitation and Light. Nature 104(2614): 354
- (1921b). The Gravitational Field of an Electron. Nature 107(2691): 392
Mie, Gustav (2007). Foundations of a Theory of Matter (Excerpts). In: The Genesis of General Relativity Ed. by Michel Janssen, John D. Norton, J.D. N., Renn John D., R. J.D.. Boston Studies in the Philosophy of Science, Volume 250. Boston: Springer 1554-1619
Nordström, Gunnar (1914). Über die Möglichkeit, das elektromagnetische Feld und das Gravitationsfeld zu vereinigen. Physikalische Zeitschrift 15: 504-506
Pais, Abraham (2000). The Genius of Science. Oxford: Oxford University Press.
Pauli, Wolfgang (1921). Relativitätstheorie. In: Enzyklopädie der Mathematischen Wissenschaften Berlin: B. G. Teubner 539-775
- (1958). Theory of Relativity. New York: Pergamon.
Planck, Max (1899). Über irreversible Strahlungsvorgänge. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin 5: 440-480
Rechenberg, Helmut (1995). Quanta and Quantum Mechanics. In: Twentieth Century Physics Ed. by Laurie M. Brown, Abraham Pais, A. P.. New York: Institute of Physics Publishing 143-248
Renn, Jürgen (2007). The Genesis of General Relativity. Dordrecht: Springer.
Rovelli, Carlo (2000). The Century of the Incomplete Revolution: Searching for General Relativistic Quantum Field Theory. Journal of Mathematical Physics 4(6): 3776-8801
- (2002). Notes for a Brief History of Quantum Gravity. In: The Ninth Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories Ed. by Vahe G. Gurzadyan, Robert T. Jantzen, R.T. J.. Singapore: World Scientific 742-768
Rowe, David E. (2003). Hermann Weyl, the Reluctant Revolutionary. Mathematical Intelligencer 25(1): 61-70
Rutherford, Ernest F., Arthur Compton (1919). Radio-Activity and Gravitation. Nature 104(2617): 412
Sanchez-Ron, Jose M. (1992). General Relativity Among the British. In: Studies in the History of General Relativity Ed. by Jean Eisenstaedt, Anne J. Kox. Boston: Birkhäuser 57-88
- (1999). Larmor versus General Relativity. In: The Expanding Worlds of General Relativity Ed. by Hubert Goenner, Jürgen Renn, J. R., Ritter Jürgen. Boston: Birkhäuser 405-430
Sauer, Tilman (2002). Hope and Disappointments in Hilbert's Axiomatic `Foundations of Physics'. In: History of Philosophy of Science Ed. by Michael Heidelberger, Friedrich Stadler. Dordrecht: Kluwer 225-237
Scholz, Erhard (2001). Hermann Weyl's Raum-Zeit-Materie and a General Introduction to His Scientific Work. Basel: Birkhäuser.
Schweber, Silvan S. (2009). Weimar Physics: Sommerfeld's Seminar and the Causality Principle. Physics in Perspective 11: 261-301
Shaw, Philip E. (1916). The Newtonian Constant of Gravitation as Affected by Temperature. Philosophical Transactions of the Royal Society of London, Series A 216: 349-392
Sommerfeld, Arnold (2000). Wissenschaftlicher Briefwechsel. Band 1. 1892–1918. Berlin: Deutsches Museum, Verlag für Geschichte der Naturwissenschaften und der Technik.
Stachel, John (1998). The Early History of Quantum Gravity (1916–1940). In: Black Holes, Gravitational Radiation and the Universe Ed. by Bala R. Iyer, Biplab Bhawal. Dordrecht: Kluwer Academic Publishers 525-534
Uhlenbeck, George, Samuel Goudsmit (1926). Spinning Electrons and the Structure of Spectra. Nature 117(2946): 264-265
Weyl, Hermann (1921). Raum-Zeit-Materie. Berlin: Julius Springer.
Wiener, Norbert (1956). I Am a Mathematician: The Later Life of a Prodigy. Cambridge, MA: MIT Press.
Wuensch, Daniela (2003). The Fifth Dimension: Theodor Kaluza's Ground-Breaking Idea. Annalen der Physik (Leipzig) 12(9): 519-542
Footnotes
See, for example (Stachel 1998) and (Rovelli 2002).
See (6.2) below on these studies. Also see (Stachel 1998), in which he considers an earlier and slightly more diverse group of actors. Another excellent study—though with a focus more on unified field theories than quantum gravity—is (Goldstein and Ritter 2003). This traditional view that quantum gravity originates with Rosenfeld can be traced back at least as far as Bryce DeWitt’s brief historical review in the first of his three Physical Review papers on quantum gravity in 1967 (DeWitt 1967).
Of course, “atomic” certainly does not mean “quantum”. However, many of the issues that were discussed in the context of merging atomic and gravitational physics are nonetheless relevant for later work on quantum gravity since they often involve overlapping concerns such as implementing discreteness, singular behavior, and so on, in the context of a theory like general relativity. For this reason I often discuss non-quantum, atomic physics. It will be clear from the context when this is the case. It is my contention that if one is looking for sources of the earliest examples of genuine quantum gravity research, then one cannot ignore these non-quantum examples.
An example of such quantum gravity without the quantization of gravity are the so-called “emergent gravity” proposals. See (Hu 2009) for a nice review of these.
Where, as I already indicated, this might sometimes be stretched to strictly non-quantum situations, such as early atomic physics when this physics has some properties relevant to the full quantum context.
These rather non-technical accounts were often duplicated in German in Naturwissenschaften.
Or, in somewhat less anachronistic terms, in the case of the very earliest such work, this was a dialogue between the puzzling behavior of discrete matter then observed to behave in an increasingly curious way, and gravitation.
For the state of the art of both quantum mechanics and general relativity, consult (Galison et.al. 2001) and (Renn 2007) respectively.
I am indebted in this section to the hard work of Leo Corry, David Rowe, Tilman Sauer and others in unpacking the complex relations between Mie, Hilbert and Weyl.
Letter from Einstein to Weyl, dated 23 November 1916, cited in (Rowe 2003, 65); see also (Sauer 2002).
See (Scholz 2001) for a fine discussion of this episode along with a translation of Weyl’s text.
Gennady Gorelik (1992) assigns the discovery that these fundamental constants might point to the limits of present physical theory to Matvei Bronstein. While I agree that Bronstein was the first to produce an explicit account of the nature of this limitation in the 1930s, I show later that Eddington also made similar claims in 1919.
A little later it would also come to be understood that there is a “formal interaction” between general relativity and quantum objects stemming from the peculiar nature of fermions, including: objects with half-integer spins imposes a variety of constraints on the space-time structure, and therefore on the gravitational field (resulting in a slightly modified theory of gravitation). This was a rather slow lesson.
Though it appears that it was Sommerfeld who led this exchange, fired up, no doubt, by the success of his application of specially relativistic principles to quantum theory.
Norbert Wiener, who would spend much time in Göttingen, also seems to have become caught up in the general need for a harmonious structure at the foundations of physics. He writes in the second volume of his autobiography that “By 1925 […] the world was clamouring for a theory of quantum effects which would be a unified whole and not a patchwork” (Wiener 1956, 105).
As Helge Kragh has pointed out, the version of quantum theory that Einstein would have been thinking about at this early phase of general relativity’s development was precisely the Bohr-Sommerfeld theory (Kragh 2000, 965). Einstein would have been particularly impressed with the way the Sommerfeld theory integrated (special) relativity and quantum theory. Helmut Rechenberg claims that Sommerfeld published his results after Einstein informed him that, as one might expect, the general relativity would not modify the results in any appreciable way (Rechenberg 1995, 160).
Though apparently not too troubled. In a letter dated 19 July 1916 (Buchwald et.al. 2006, Vol. 10, 237a, 25) he writes breezily to his friend Heinrich Zangger after just completing this work (and his contemporaneous work on the quantum theory of emission and absorption of radiation), showing no signs of real concern over the fate of general relativity—though it is also very possible that his mind was preoccupied with the breakup of his marriage at this point.
This openness of Einstein to the possibility of a quantum theoretical modification of general relativity would not last long of course, and was already beginning to sour at this stage. His taste for quantum theory soon dissolved to the extent that towards the end of his life, he was searching for ways to reproduce quantum mechanical phenomena using a purely classical field theory. Suraj Gupta (who developed a special-relativistic theory of quantum gravity in the 1950s) has a different (inverted) interpretation of Einstein’s underlying reasons for distrusting quantum mechanics: “Because his theory is different from other field theories, he tried to construct unified field theories and because he could not see how his theory in the curved space could possibly be quantized, he criticized quantum mechanics” (Gupta 1962, 253).
For example, Goldstein and Ritter (2003, 104) note how Weyl (1921) adopts this position in his Raum, Zeit, Materie, for which see (Scholz 2001).
To reiterate what was said in the introduction, I am not solely focusing on proposals that aim to unite quantum theory and gravitation in a common framework. Rather, I am concerned with showing how quantum theory and quantum phenomena and general relativistic phenomena and general relativity did not occupy isolated conceptual schemes in the minds of physicists at this time but were very much intertwined. This often manifests itself in ways that have persisted into modern thinking on the problem of quantum gravity, such as the notion that merging quantum theory and general relativity might serve to resolve some internal problem with one or another ingredient theory. However, I also include less obviously interesting examples indicating merely that the problem of linking the two theories together was “in the air” so that the later work of Rosenfeld, for example, is seen as a fairly natural problem to focus on.
This quest has been discussed in some detail by several authors. Clive Kilmister (a student of a student of Eddington, namely George McVittie) focuses directly on Eddington’s concern with the relation between gravity and quantum theory (Kilmister 1994). Ian Durham (2003) focuses more on Eddington’s desire to achieve an objective account of physics independently of human measures.
Note that the value he derives is some six orders of magnitude off from the value we have today (namely
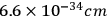 ). Note also that Eddington does not mention Planck’s name, so one might wonder whether he came to the result (of a system of unique scales from combining these three constants) independently of Planck (1899). Of course, the idea that there is a smallest length would later become a common feature of quantum gravitational physics—Kragh (2000) provides a useful study of the earliest work (based on quantum considerations) on the notion of a minimal length. I might also add that Eddington is a missing figure from Gorelik’s otherwise superb recounting of the history of the role of the Planck units in the early history of quantum gravity research (Gorelik 1992).
). Note also that Eddington does not mention Planck’s name, so one might wonder whether he came to the result (of a system of unique scales from combining these three constants) independently of Planck (1899). Of course, the idea that there is a smallest length would later become a common feature of quantum gravitational physics—Kragh (2000) provides a useful study of the earliest work (based on quantum considerations) on the notion of a minimal length. I might also add that Eddington is a missing figure from Gorelik’s otherwise superb recounting of the history of the role of the Planck units in the early history of quantum gravity research (Gorelik 1992).
Of course, these units derive initially from Planck’s system of “absolute units” (Planck 1899). But in that paper, Planck does not link this to any synthesis of quantum theory and gravitation, nor did he suggest that the absolute unit of length imposed any lower limit on objects and processes. He was, rather, impressed with their independence from the usual conventional elements involved in “terrestrial” units. That the units are just “pure numbers” encoding the laws of physics must have impressed Eddington, for just this connection would form the basis of his later (near-numerological) work on deriving the laws of physics from such pure numbers, in his last book Fundamental Theory, for example (Eddington 1949). I suspect (though it is not the place to discuss here) that this early realization about absolute units and their relationship with (objective descriptions of) physical laws might have played a greater role in Eddington’s later work than has previously been realized.
See (Halpern 2004) for a discussion of the (lack of) impact of Nordström’s proposal.
Daniela Wuensch points out that Larmor’s paper appeared before Kaluza’s, but argues that because Larmor had used flat space-time, it did not excite much interest (Wuensch 2003, 526). I do not think this can be the right explanation: Larmor’s approach involves flat Minkowski space only as a projective feature of the world. I find it more likely that both the cumbersome nature of the approach, the novelty and the heavily abstract formulation were more likely to be the reason that the approach did not catch on.
The section “On Gravitational Relativity,” from which this set of quotations was taken, was added by Larmor on 20 November 1919. All emphasis added by the author.
Frederick G. Donnan deduced a relation between “the variation of mass in a physical change of state or chemical reaction and the rate of variation with gravitational potential of the corresponding change of total internal energy” (Donnan 1919, 392). Note there was a general concern around this time with the source of stellar energy. It is thus fairly natural to consider the possible dependence of the rate of emission on the star’s gravitational field.
They got as far as a method of testing radioactive decay rates (over a period of up to 100 days), and were planning on sending their various radioactive substances to parts of the world with significant differences in their gravitational field strength.
Sanchez-Ron (1992, 68) claims that Rutherford and Compton “did not make any effort to see whether or not their experimental results agreed with the predictions of general relativity.” However, the previous remark clearly states that, for processes of such microscopic nature, it would be a practical impossibility to compare the experimental results with the theory beyond the very broad fact that no result is expected to be seen on the basis of general relativity.
However, the same question was tackled in 1942, with the benefit of new theoretical knowledge and improved experimental techniques (then able to produce centrifugal fields of 1000000
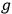 ), by Freed, Jaffey and Schultz (1942)—they explicitly cite the Cavendish results in their work. Even at these centrifugal field strengths, no effect was seen that could be distinguished from experimental error. For a discussion on how this early experimental research developed into the modern era of quantum gravity research, see (Gillies and Unnikrishnan 2002a; 2002b), especially p.127 of the latter.
), by Freed, Jaffey and Schultz (1942)—they explicitly cite the Cavendish results in their work. Even at these centrifugal field strengths, no effect was seen that could be distinguished from experimental error. For a discussion on how this early experimental research developed into the modern era of quantum gravity research, see (Gillies and Unnikrishnan 2002a; 2002b), especially p.127 of the latter.
Curiously, John Joly returned to the general issue of the connection between rates of radioactive decay and the principle of relativity posing the question of whether radioactive clocks might offer an invariant way to measure absolute time, or whether “radio-activity [is] also ‘in the conspiracy’” (Joly 1920, 468). Clearly the centrifugal experiments were not sufficient to determine the answer one way or the other. Of course, it was only fairly recently that the question was answered and the effect of gravitational time dilation on atomic clocks was confirmed (Hafele and Keating 1972).
Recall that at this time electromagnetism alone was thought to be responsible for the structure of matter.
Jeans’s examples are based on radiation, involving the disintegration of uranium and Einstein’s own work on the emission and absorption of light quanta (described by Jeans as “the statistics of their jumping about”); with such phenomena, says Jeans, “we seem to be beyond the domain of […] natural laws” (Jeans 1926, 311).
Klein claims that Bohr had earlier made similar suggestions (Klein 1991, 109). However, he recalls his later discussions with Bohr and Heisenberg as being received with “kind skepticism” (Klein 1991, 112).
Klein (1991, 112) notes that Ehrenfest had asked Lorentz to invite Klein (on a Lorentz Fellowship) after having read a copy of Klein’s paper that was given to him by Llwellyn Hilleth Thomas (himself passing through Leiden on his way from Copenhagen to Cambridge). Uhlenbeck refers to an unpublished paper between himself, Ehrenfest, and Klein (see interview of Uhlenbeck by Thomas S. Kuhn on 9 December 1963, Niels Bohr Library & Archives). Uhlenbeck recalls that at the time he believed Klein had something like a theory of everything: “It seemed then that one was very close to a world formula—one equation containing everything, you see. I remember that I had the feeling that ‘Golly, we now perhaps know everything’” (Klein 1991, 112)—though he notes that the same was not true of Ehrenfest.
The
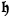 term here is Kaluza’s expression for the
term here is Kaluza’s expression for the
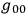 th component (i.e., the “corner potential”) of the metric tensor;
th component (i.e., the “corner potential”) of the metric tensor;
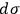 is a five-dimensional Riemannian line-element (given by
is a five-dimensional Riemannian line-element (given by
 );
);
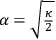 , with
, with
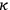 the gravitational constant.
the gravitational constant.
Hence, this is far more radical than Einstein intimated in his question over whether the interior of atoms is non-Euclidean.
See e.g., (Ashtekar 2005).
