After its appearance in the context of radiation theory, the quantum hypothesis rapidly diffused into other fields. By 1910, the crisis of classical traditions of physics and chemistry—while taking the quantum into account—became increasingly evident. The First Solvay Conference in 1911 pushed quantum theory to the fore, and many leading physicists responded by embracing the quantum hypothesis as a way to solve outstanding problems in the theory of matter.
Until about 1910, quantum physics had drawn much of its inspiration
from two sources. The first was the complex formal machinery connected with Max Planck’s theory of radiation and, above all, its close relationship with probabilistic arguments and statistical mechanics. The fledgling 1900–1901 version of this theory hinged on the application of Ludwig Boltzmann’s 1877 combinatorial procedure to determine the state of maximum probability for a set of oscillators. In his 1906 book on heat radiation, Planck made the connection with gas theory even tighter. To illustrate the use of the procedure Boltzmann originally developed for an ideal gas, Planck showed how to extend the analysis of the phase space, commonplace among practitioners of statistical mechanics, to electromagnetic oscillators (Planck 1906, 140–148). In doing so, Planck identified a crucial difference between the phase space of the gas molecules and that of oscillators used in quantum theory. Whereas in Boltzmann’s statistical mechanics, a state corresponds to an arbitrarily small cell of the phase space, defined by a system’s coordinates and momenta, the quantum hypothesis requires a partition of the space into elementary regions—or volume elements—each equal to Planck’s constant,
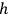 . As we demonstrate below, phase space quantization enabled extending the quantum hypothesis to systems whose complexity exceeded that of oscillators. However, by 1906, Planck did not draw any conclusion about the phase space of gas molecules.
. As we demonstrate below, phase space quantization enabled extending the quantum hypothesis to systems whose complexity exceeded that of oscillators. However, by 1906, Planck did not draw any conclusion about the phase space of gas molecules.
The other source was Albert Einstein’s 1907 theory of solids, the first successful application of the quantum hypothesis outside the realm of heat radiation (Einstein 1907). By assuming that the particles of a solid behave like oscillators whose energy is given by Planck’s radiation formula, Einstein was able to derive a temperature dependence of a solid’s specific heat that agreed qualitatively with Nernst’s theorem (see below). Einstein’s theory demonstrated that the quantum hypothesis could be used to solve outstanding problems in the theory of matter. Among its descendants are the nearly-definitive theories of the thermal properties of solids developed by Peter Debye in 1912 and by Max Born and Theodore von Kármán in 1912–1913.
From the close link between the gas and the oscillators mentioned above, one may get the impression that the leap to the quantum theory of a monoatomic gas was a fairly intuitive process. However, this was not the case, because of conceptual difficulties: its advanced formal apparatus notwithstanding, the quantum hypothesis was conceived for periodic systems characterized by a frequency. Viewed as a swarm of whirling particles, a gas was thus understood as the opposite of a paradigmatic quantum system. For instance, in 1911 Nernst resolutely denied the possibility of quantizing translation (Nernst 1911, 267), although he had advocated the extension of quantum theory to gases.1 Furthermore, there was no experimental motivation for extending the quantum hypothesis to a monoatomic gas. As late as 1913, Arnold Eucken pointed out that no genuine quantum phenomenon had yet been observed involving such a system (Eucken 1914, 396–397).
It is no wonder that in the early twentieth century the quantum theory of a gas was more of a concern to outsiders, such as Otto Sackur, rather than to such experts as Einstein or Planck. The first attempts to develop a quantum theory of a gas thus came about in response to concerns about peripheral issues, namely chemical equilibria, instead of arising from an interest in revamping kinetic theory or thermodynamics.
Indeed, the emergent quantum framework compelled a host of young researchers to approach the problem of a gas with a pragmatic attitude: without an interest or resources to partake in the big foundational debates of the time, they ventured to squeeze an essence that could serve the specific goals of their research from the nascent quantum theory. This pragmatic attitude spurred a variety of applications of the quantum that, to the modern eye, may appear sloppy and naive, but that sometimes led to genuine progress.
Herein, we discuss one remarkable example of such a pragmatic approach, namely Sackur’s exploits in the quantum theory of gases. Sackur’s work was discussed in previous historical accounts;2 in this paper, however, we delve deeper into his theories to uncover aspects of his style of work which were representative for part of the quantum community. A characteristic trait of this style is Sackur’s use of quantum theory as a tool to tackle a problem deeply rooted in classical physics, specifically the chemical equilibrium in gaseous systems. Sackur’s goal-oriented attitude was partly responsible for some formal and conceptual inaccuracies and contributed to making his papers look tentative. However, his bold attempt to deploy the quantum hypothesis across classical statistical mechanics eventually proved instrumental in preparing Planck’s path to the theory of a quantum gas.
Sackur’s work developed along two non-orthogonal directions, driven on the one hand by his interest in the Nernst theorem, statistical mechanics and the problem of chemical equilibrium, and on the other, his goal to shed light on classical mechanics from a quantum vantage point. Inspired by the interplay between classical physics and quantum theory, Sackur chanced to expound his personal take on the role of the quantum in the changing landscape of physics. In this paper, we tell the story of this enthusiastic practitioner of the old quantum theory.
3.1 Biographical Overview
Otto Sackur was born in Breslau (now Wrocław), Silesia, on 29 September 1880.3 He studied chemistry first at the University of Breslau. The Chemistry Department, headed by Albert Ladenburg (1842–1911) since its foundation in 1897, was among the most prestigious in Germany. In Breslau, Sackur found an enlightened mentor, Richard Abegg (1869–1910), who introduced him to modern physical chemistry. Sackur further advanced his chemistry education at Heidelberg and Berlin before receiving his doctorate from Breslau on 31 July 1901.
Sackur’s academic career at Breslau took a detour, first via the Kaiserliches Gesundheitsamt in Berlin (October 1902 – October 1904), where he worked under the direction of Theodore Paul on problems related to public health. Subsequently, he joined William Ramsey’s laboratory at the University College London (October 1904 – March 1905) and then Walther Nernst’s new laboratory at Berlin University (March 1905 – September 1905). During the latter stays, he became privy to the most up-to-date work in physical chemistry.
Upon his return to Breslau in October 1905, he obtained his Habilitation and the title of Privatdozent. For some years, he taught at Breslau and worked side by side with Abegg, with an eye at a more secure position. Sackur’s hopes were shattered by two unfortunate events. In 1909, Ladenburg had retired because of poor health (he died two years later) and the new director of the department, the 1907 Nobel Prize winner Eduard Buchner (1860–1917), a fermentation biochemist, had little sympathy for physical chemistry. A year later, Richard Abegg died tragically in a ballooning accident.4 Without an academic sponsor and a laboratory, Sackur had to rely on his pedagogical skills to survive. He accepted minor teaching assignments, devised a course of chemistry for dentists and wrote textbooks on thermodynamics5 while trying desperately to keep abreast of the latest developments in physical chemistry. It was during this period of existential difficulties that Sackur launched his research at the intersection of physical chemistry, thermodynamics and quantum theory in the hope of a reward—a more senior academic appointment.
His hopes were fulfilled at the end of 1913, when, thanks in part to Clara Immerwahr, Fritz Haber’s first wife and Abegg’s former student, Sackur received a call to Haber’s Kaiser-Wilhelm-Institut für Physikalische Chemie und Elektrochemie in Berlin. In 1914, he was promoted to the rank of department director. After the outbreak of the Great War, Sackur was enlisted in military research at Haber’s institute, but succeeded in carrying on with his experiments on the behavior of gases at low temperatures as a side-project. On 17 December 1914, while working on a military-related project in his laboratory, Sackur was killed by an explosion at his work bench. He was only 34 years old.
3.2 The Problem of Chemical Equilibrium
In the course of the nineteenth century, the concept of a chemical equilibrium underwent several transformations. Around 1850, the old notion that a reaction is at equilibrium when all the “chemical forces” involved are balanced was gradually replaced by a kinetic view: a (reversible) chemical reaction never stops completely, but only reaches a stationary state when the reaction rates in the forward and backward directions become equal.
The ratio between the forward and backward rates was termed the equilibrium constant,
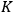 . In 1864, Cato Maximillian Guldberg (1836–1902) and Peter Waage (1833–1900) discovered that the equilibrium constant depended on the ratio of the concentrations of the reactants and products (“law of mass-action”). Their pioneering paper, published originally in Norwegian, was largely ignored until 1877, when Wilhelm Ostwald (1853–1932) adopted the law and corroborated its validity by his own experiments.6 Jacobus Henricus van’t Hoff (1852–1911) discovered the law independently in 1884 and two years later derived a formula that governs the temperature dependence of
. In 1864, Cato Maximillian Guldberg (1836–1902) and Peter Waage (1833–1900) discovered that the equilibrium constant depended on the ratio of the concentrations of the reactants and products (“law of mass-action”). Their pioneering paper, published originally in Norwegian, was largely ignored until 1877, when Wilhelm Ostwald (1853–1932) adopted the law and corroborated its validity by his own experiments.6 Jacobus Henricus van’t Hoff (1852–1911) discovered the law independently in 1884 and two years later derived a formula that governs the temperature dependence of
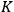 (Van ' t Hoff 1886).
(Van ' t Hoff 1886).
A second breakthrough in the study of chemical equilibria occurred in the 1880s, when thermodynamics was applied to chemical problems. As early as 1878, Josiah Willard Gibbs (1839–1903) used the concept of the maximum work produced by a reaction to define chemical equilibrium: a reaction has reached a stationary state when it produced all the work it was capable of producing (Gibbs 1878). Curiously, Gibbs faced a fate similar to that of Guldberg and Waage’s, since the publication of his results in an obscure journal hampered their dissemination. In 1882, Hermann von Helmholtz (1821–1894) arrived at the same results independently. He distinguished between a bound and a free energy of a system. The latter is transformed into work during a chemical reaction, whose equilibrium is reached when the free energy drops to its minimum value (von Helmholtz 1882). As Arnold Eucken paraphrases it:
[T]he (maximum) work represents a quantity whose knowledge leads immediately to the solution of the [equilibrium problem]: only when a chemical process is able to perform work, it will go on spontaneously. Hence, one can also say in what direction [a reaction] develops, if it is given in which transformation […] the maximum work has a positive sign. If in a chemical transformation no work is produced, then the system is in a state of equilibrium. (Eucken 1922, 123)
The concept of free energy amounted to a well-founded overhaul of the old intuitive notion of “affinity.” The internal energy,
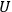 , of a chemical system is made up of free energy,
, of a chemical system is made up of free energy,
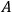 , that can be used to produce work and of bound energy (also called the “latent heat of reaction”),
, that can be used to produce work and of bound energy (also called the “latent heat of reaction”),
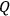 . At equilibrium, the reaction work and the equilibrium constant are related by the equation
. At equilibrium, the reaction work and the equilibrium constant are related by the equation
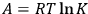
|
3.1 |
with
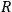 the universal gas constant and
the universal gas constant and
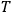 the absolute temperature.
the absolute temperature.
By combining the first and second laws of thermodynamics for the case of an isothermal and isochoric gaseous reaction, it was possible to obtain the following equation, sometimes called the Helmholtz equation, for the free energy,
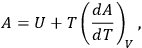
|
3.2 |
where
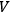 is the volume (Haber 1905, 18–22). The general integral of this equation is:7
is the volume (Haber 1905, 18–22). The general integral of this equation is:7
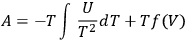
|
3.3 |
with
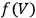 the integration constant (integration at constant volume). Thus, to evaluate the free energy—and, via eq. (3.1), the equilibrium constant—one had to determine, at a given temperature, the reaction energy
the integration constant (integration at constant volume). Thus, to evaluate the free energy—and, via eq. (3.1), the equilibrium constant—one had to determine, at a given temperature, the reaction energy
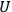 and the function
and the function
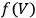 . Experimentally, this task was far from easy and much effort was expended in the final decades of the nineteenth century at collecting the requisite data for various substances.8
. Experimentally, this task was far from easy and much effort was expended in the final decades of the nineteenth century at collecting the requisite data for various substances.8
The Heat Theorem, enunciated by Walther Nernst (1864–1941) in 1906, amounted to a third breakthrough.9 Nernst observed that as
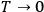 , the slopes of the temperature dependence of the free energy and of the internal energy (heat) tend asymptotically to the same limit,10 without concluding that
, the slopes of the temperature dependence of the free energy and of the internal energy (heat) tend asymptotically to the same limit,10 without concluding that
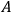 and
and
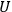 themselves become equal at
themselves become equal at
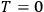 as well. Nevertheless, based on his observation, Nernst was able to set the integration constant
as well. Nevertheless, based on his observation, Nernst was able to set the integration constant
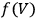 in eq. (3.3) to zero (Nernst 1906a; 1906b) and thereby find at any temperature
in eq. (3.3) to zero (Nernst 1906a; 1906b) and thereby find at any temperature
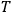 the free energy
the free energy
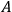 from
from
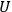 which could, in turn, be determined from thermochemical data.11
which could, in turn, be determined from thermochemical data.11
However, the experimental data as well as the theoretical arguments that supported Nernst’s assumptions could not be extrapolated to a gas at very low temperatures and held true only for condensed-matter systems.12 The treatment of the equilibrium of gaseous reactions remained beyond the direct reach of the theorem. In response, Nernst devised an ingenious detour which made it possible to evaluate the equilibrium constant of gaseous reactions as well. Nernst noticed that the integration constant,
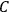 , of the Van’t Hoff equation was closely related to the integration constant of the Clausius-Clapeyron equation which governs the temperature dependence of pressure of a vapor in phase equilibrium with a liquid or solid condensate (the two equations are isomorphic). Nernst dubbed this quantity the chemical constant (Nernst 1906a, 22). The chemical constant had to be determined experimentally for each gaseous species
, of the Van’t Hoff equation was closely related to the integration constant of the Clausius-Clapeyron equation which governs the temperature dependence of pressure of a vapor in phase equilibrium with a liquid or solid condensate (the two equations are isomorphic). Nernst dubbed this quantity the chemical constant (Nernst 1906a, 22). The chemical constant had to be determined experimentally for each gaseous species
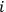 involved in the reaction, which was indeed possible thanks to the absolute character of entropy, as established by Nernst’s theorem (see below, section 3). Once the
involved in the reaction, which was indeed possible thanks to the absolute character of entropy, as established by Nernst’s theorem (see below, section 3). Once the
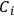 ’s are available, the equilibrium constant of a gaseous reaction follows:
’s are available, the equilibrium constant of a gaseous reaction follows:
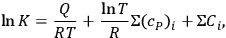
|
3.4 |
where
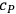 is the heat capacity at constant pressure. To evaluate the chemical constant, Nernst attempted to express it as a function of the thermochemical parameters by resorting to various approximations of the Clausius-Clapeyron equation (Nernst 1907, 55–76). However, by 1911, the chemical constants were available for only a handful of substances. This was chiefly
due to the unreliability of the approximations involved and to the great difficulties encountered when performing measurements at cryogenic temperatures. Sackur followed a different strategy. In 1911 he commented:
is the heat capacity at constant pressure. To evaluate the chemical constant, Nernst attempted to express it as a function of the thermochemical parameters by resorting to various approximations of the Clausius-Clapeyron equation (Nernst 1907, 55–76). However, by 1911, the chemical constants were available for only a handful of substances. This was chiefly
due to the unreliability of the approximations involved and to the great difficulties encountered when performing measurements at cryogenic temperatures. Sackur followed a different strategy. In 1911 he commented:
Only Nernst’s theorem makes it possible to establish the constantwhich determines the chemical behavior of gases from measurements on pure substances (vapor pressure of liquids or solids) and thereby […] also the entropy constant [
]. (Sackur 1911b, 965)
The reference to the entropy constant is key: Sackur recognized that the vapor-condensate system can be dealt with by applying the second law of thermodynamics, which leads to a simple relation between the integration constant of the entropy and the chemical constant:
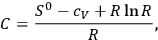
|
3.5 |
where
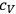 is the specific heat of a gaseous component at constant volume and
is the specific heat of a gaseous component at constant volume and
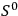 its entropy constant, see eq. (3.10) below.
its entropy constant, see eq. (3.10) below.
This relation is at the core of Sackur’s 1911 advance: he set out to calculate the entropy constant
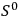 —and thus
—and thus
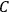 —by invoking statistical mechanics. This was a bold move not only because of the rather tentative status of the statistical approach at the time but also because entropy itself was perceived as difficult to define and, moreover, wedded to “mysterious” applications of probability. Physical chemists of the time preferred the concept of maximum work to characterize chemical equilibrium. In the most influential physical chemistry textbook of the time, Nernst’s Theoretische Chemie, entropy comes up only to be brushed away as dispensable. However, Sackur’s move was not unrewarded: he was able to derive the first quantum-statistical expression for the entropy of an ideal gas (in the limit of high temperatures and low densities). A similar expression was discovered independently at about the same time by Hugo Tetrode (1895–1931) and is known as the Sackur-Tetrode equation. The Sackur-Tetrode equation made it possible to evaluate the entropy constant and thus the chemical constant in terms of better-known quantities.
—by invoking statistical mechanics. This was a bold move not only because of the rather tentative status of the statistical approach at the time but also because entropy itself was perceived as difficult to define and, moreover, wedded to “mysterious” applications of probability. Physical chemists of the time preferred the concept of maximum work to characterize chemical equilibrium. In the most influential physical chemistry textbook of the time, Nernst’s Theoretische Chemie, entropy comes up only to be brushed away as dispensable. However, Sackur’s move was not unrewarded: he was able to derive the first quantum-statistical expression for the entropy of an ideal gas (in the limit of high temperatures and low densities). A similar expression was discovered independently at about the same time by Hugo Tetrode (1895–1931) and is known as the Sackur-Tetrode equation. The Sackur-Tetrode equation made it possible to evaluate the entropy constant and thus the chemical constant in terms of better-known quantities.
3.3 The Beginnings of the Quantum Theory of Gases
In the first decade of the twentieth century, many proponents of the quantum, such as Nernst, Max Planck (1858–1947), and Albert Einstein (1879–1955), had come to think that kinetic theory, quantum theory, the heat theorem, statistical mechanics and (physical) chemistry were all closely related. Einstein’s 1907 quantum theory of solids exemplifies the power of the quantum in treating what used to be known as the kinetic theory of matter, while Nernst, at about the same time, became convinced that the quantum implied the validity of his theorem for gases.13 On a more general level, it became apparent that the quantum called for new ways of applying statistical mechanics to both the theory of radiation and the theory of matter.
Presumably, Sackur learned about these developments at the scientific meetings he had attended tirelessly in those years.14 The approach to the theory of matter based on sophisticated mathematical techniques—which quantum theory entailed—was exactly his “cup of tea.” Unlike the majority of physical chemists of the time who had an aversion to the formal complications of kinetic theory (including major protagonists such as Nernst), Sackur was convinced that physical chemistry could not do without the most advanced mathematical tools available. During his academic career in Breslau, he taught classes in both kinetic theory (summer semesters 1910 and 1912) and in the “Mathematical Treatment of Chemistry” (winter semester 1906 and summer semester 1908). Sackur’s lecture notes became the basis for an acclaimed book written jointly with Abegg, which was translated into English (Abegg and Sackur 1909).
In Sackur’s usage, the term “kinetic theory” did not refer to the nineteenth-century analysis of collisions leading to the riddle of irreversibility. Instead, kinetic theory meant an attempt to trace the thermal behavior of systems, chemical or other, to the arrangements of their molecules. This is illustrated by his first paper dedicated to such problems (Sackur 1911a).15 Sackur argued that with decreasing temperature, the available molecular energy becomes increasingly restricted, limiting the number of “cells” (states) over which the molecules can be distributed. When the temperature drops close to zero, the number of cells approaches one, as a result of which the distribution becomes ordered: all the molecules end up herded in the last remaining cell. Since entropy depends on the number of molecular arrangements,
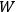 , via the Boltzmann principle
, via the Boltzmann principle
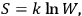
|
3.6 |
it was apparent that
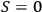 for
for
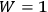 when all the molecules are in the same cell. Since Nernst’s theorem can be expressed as
when all the molecules are in the same cell. Since Nernst’s theorem can be expressed as
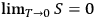 (Planck 1911, 266–286), Sackur concluded that the third law reduces to the claim that low-temperature molecules are arranged in their energy space in the most orderly fashion.
(Planck 1911, 266–286), Sackur concluded that the third law reduces to the claim that low-temperature molecules are arranged in their energy space in the most orderly fashion.
The main sources of inspiration for Sackur’s paper (Sackur 1911a) were precisely those mentioned in the introduction: Planck’s 1906 Wärmestrahlung as well as Einstein’s 1907 theory of solids (Einstein 1907). Sackur was especially intrigued by the way Einstein intertwined the classical statistico-mechanical approach with the new quantum hypothesis. In the second part of the paper, Einstein proposed a second proof of the heat theorem by showing that the quantum hypothesis, in the case of a solid, implied that the entropy constant is zero. For Sackur, the transition from the gas to the solid was justified by Einstein’s general procedure:
[A] complete kinetic theory of the solid state of aggregation might perhaps be built on Einstein’s presuppositions, just as the van der Waals’ theory was built on the presuppositions of the classical gas theory. (Sackur 1911a, 467)
Furthermore, Sackur’s paper attests to its author’s internalization of Planck’s concept of absolute entropy. Classical thermodynamics defines only an entropy difference and leaves the integration constant undetermined. But Planck was convinced that entropy expresses a fundamental property of nature and, therefore, must have an absolute value. Quantum theory combined with the heat theorem affirmed that entropy’s integration constant can be set to zero.16
Sackur adopted the concept of absolute entropy and used it as a building block of his new quantum theory of the ideal gas. In his second 1911 paper, he tried to construct a general application of his peculiar version of kinetic theory to chemical problems. Here “application” expresses the second direction of Sackur’s work: his attempt to transform abstract procedures into potent treatments of classical problems. To Sackur, the glue that holds together quantum theory, kinetic theory and physical chemistry is the concept of probability, whose value was well proven in investigations of gases and could be applied to other problems as well:
This idea has been hitherto applied only to the variations of state of an ideal gas, that is to physically and chemically uniform substances, as well as to radiation phenomena. Now it seems that it can be applied to any spontaneously occurring processes in nature, for example to chemical reactions and to irreversible processes of any kind that are connected with an increase of the probability of a closed system. This generalization of the concept of probability to chemically distinct states of matter appears to me as a simple consequence of Boltzmann’s view. (Sackur 1911b, 960)
Henceforth, Sackur set out to find a general way of comparing the probability of different states. The case of chemical equilibrium in an ideal gas was particularly suitable for this aim, as it went just a step beyond Boltzmann’s gas theory.
In his attack on the problem of entropy from the kinetic side, Sackur explicitly follows Planck’s statistico-mechanical treatment of an ideal gas based on the partitioning of the phase space. In classical statistical mechanics, the state of the gas is determined by the number of molecules whose coordinates lie between
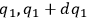 ,
,
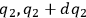 and
and
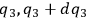 , while their velocity components lie between
, while their velocity components lie between
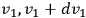 ,
,
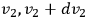 , and
, and
 . Thus, if the state space of a single molecule is divided into “elementary regions”
. Thus, if the state space of a single molecule is divided into “elementary regions”
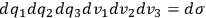 , and
, and
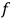 is the distribution function of the number of molecules in that state space, the number of molecules in a given “elementary region” is
is the distribution function of the number of molecules in that state space, the number of molecules in a given “elementary region” is
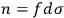 . Let us assume that the elementary regions
. Let us assume that the elementary regions
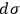 can be numbered and that
can be numbered and that
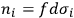 is the number of molecules contained in the
is the number of molecules contained in the
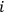 -th region. Thus a state distribution is the sequence
-th region. Thus a state distribution is the sequence
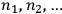 of the occupation numbers of each region. In 1877, Boltzmann proposed a simple recipe to calculate the probability of such a distribution, namely by counting the number of ways in which one can permute the molecules between different regions without changing the overall distribution. From combinatorics, this number turns out to be:
of the occupation numbers of each region. In 1877, Boltzmann proposed a simple recipe to calculate the probability of such a distribution, namely by counting the number of ways in which one can permute the molecules between different regions without changing the overall distribution. From combinatorics, this number turns out to be:
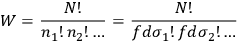
|
3.7 |
where
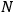 is the number of molecules. By substituting for
is the number of molecules. By substituting for
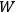 in the Boltzmann principle, eq. (3.6), invoking the Stirling formula, setting
in the Boltzmann principle, eq. (3.6), invoking the Stirling formula, setting
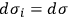 for all
for all
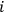 , and replacing summation by integration,17 Sackur arrived at the formula for entropy
, and replacing summation by integration,17 Sackur arrived at the formula for entropy
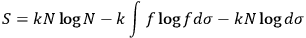
|
3.8 |
whose maximum (which corresponds to equilibrium) yields the distribution function
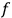 . Under the constraints of constant energy and number of molecules,
. Under the constraints of constant energy and number of molecules,
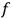 comes out Maxwellian, and substituted back into eq. (3.8), a formula for the translational entropy of a monoatomic gas results,
comes out Maxwellian, and substituted back into eq. (3.8), a formula for the translational entropy of a monoatomic gas results,
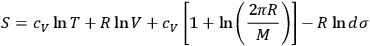
|
3.9 |
with
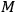 the molecular weight. A comparison of eq. (3.9) with that for the entropy of an ideal gas,
the molecular weight. A comparison of eq. (3.9) with that for the entropy of an ideal gas,
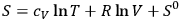
|
3.10 |
yields the entropy constant in terms of the universal gas constant, the molecular weight, and the elementary region
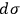 ,
,
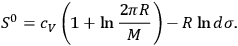
|
3.11 |
So far, the argument only used well-established elements of kinetic theory and statistical mechanics. Among the ingredients contributing to the entropy constant, only the volume of the elementary region could not be specified within the framework of classical physics. Hence a determination of the entropy constant, and therefore of the chemical constant, called for a closer investigation of this notion. So what were Sackur’s elementary regions?
3.4 Sackur’s “Elementary Regions”
A considerable part of Sackur’s paper (Sackur 1911b) deals with the properties of the elementary regions. First, he points out that the volume
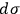 must have a well-defined value because the entropy constant is related to the equilibrium constant, which is indeed a constant for any given reaction. This requirement hinted to Sackur that the issue crosses beyond the boundaries of classical physics.
must have a well-defined value because the entropy constant is related to the equilibrium constant, which is indeed a constant for any given reaction. This requirement hinted to Sackur that the issue crosses beyond the boundaries of classical physics.
[S]ince pure kinetic [theory] has hitherto not been able to say anything about the magnitude of, there is a gap in the sequence of inferences that lead from the kinetic hypothesis to the equation of state of a gas. (Sackur 1911b, 968)
Sackur, however, did not immediately suggest that the fixed volume of an elementary region is determined by Planck’s constant,
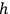 . There might be a purely technical reason for his reluctance to do so. Following Boltzmann and Planck, Sackur worked with the position-velocity space whose volume element did not have the dimension of action. In fact, Sackur carried out the dimensional analysis of the entropy constant, but he limited himself to verifying that it depended on the volume of the gas in the expected way. Although noncommittal as to the physical meaning of
. There might be a purely technical reason for his reluctance to do so. Following Boltzmann and Planck, Sackur worked with the position-velocity space whose volume element did not have the dimension of action. In fact, Sackur carried out the dimensional analysis of the entropy constant, but he limited himself to verifying that it depended on the volume of the gas in the expected way. Although noncommittal as to the physical meaning of
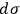 , the peculiarity of a fixed-magnitude elementary volume did not escape Sackur’s attention. He tried to give both a visual and a conceptual interpretation of this result.
, the peculiarity of a fixed-magnitude elementary volume did not escape Sackur’s attention. He tried to give both a visual and a conceptual interpretation of this result.
Visually, the fixed-magnitude volume seems to entail that molecules do not pass smoothly from one state to another, or equivalently, that they do not spread out into the entire space allowed:18
The gas molecules do not distribute themselves uniformly over the whole allowed space and they cannot have all possible velocities from zero to infinity, but […] they concentrate around individual points in space, like bullets on a target, and […] their velocity components change in jumps. (Sackur 1911b, 969)
Here we encounter a characteristic trait of Sackur’s approach. Drawing on the “visualizability” of a discrete space, Sackur initially presumes a discontinuous behavior of the molecules. But in reality, his underlying picture remained a provisional sketch. As we show in the next section, he eventually dropped discontinuity and moved toward an operational approach which sidestepped precise commitments about the microscopic nature of gas particles. This was due not only to the objective difficulties of framing a clear picture of the quantum phenomena, but went hand in hand with the problem-oriented character of his program. The motivation behind his research was the idea of putting the quantum in the service of classical problems—and not developing an understanding of the quantum’s nature.
Conceptually, Sackur relied on Planck and traced the “atomicity” of the elementary region back to the calculation of probability. In his 1900 paper in which he enunciated the quantum hypothesis, Planck argued that an actual computation of a state’s probability is possible only if the total energy is divided into elements of a finite size. The atomicity of energy then followed directly from the Boltzmann relation between entropy and probability, eq. (3.6). Sackur subscribed to Planck’s view unconditionally:
[E]ither [we] postulate the physical reality of a finite elementary region (and of finite elementary quanta) or [we] give up the unequivocal relation between entropy and probability. (Sackur 1911b, 970)
Sackur’s prime interest, however, lay in the physico-chemical properties of the elementary regions
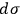 . Coming to terms with what
. Coming to terms with what
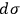 means is the theme of the second part of his analysis, whose conclusion is twofold: First,
means is the theme of the second part of his analysis, whose conclusion is twofold: First,
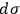 is not a universal constant but must somehow depend on the molecular mass. By combining eqs. (3.5) and (3.11), Sackur obtained
is not a universal constant but must somehow depend on the molecular mass. By combining eqs. (3.5) and (3.11), Sackur obtained
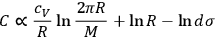
|
3.12 |
and argued that if
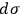 were the same for all gases with the same number of molecules (as
were the same for all gases with the same number of molecules (as
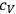 is), then the chemical constant
is), then the chemical constant
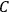 would have to decrease with increasing molecular weight. This, however, would contradict Nernst’s experiments, which had found that
would have to decrease with increasing molecular weight. This, however, would contradict Nernst’s experiments, which had found that
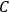 in fact increases with
in fact increases with
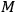 .
.
Second, Sackur concluded that
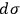 depends on the number of molecules. By making use of an ingenious argument,19 Sackur contended that the probability of an ideal gas consisting of
depends on the number of molecules. By making use of an ingenious argument,19 Sackur contended that the probability of an ideal gas consisting of
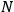 molecules partitioned into
molecules partitioned into
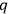 subsystems with
subsystems with
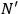 molecules each and probability
molecules each and probability
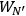 has a total probability
has a total probability
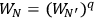 . An application of Boltzmann’s principle then led Sackur to the conclusion
that the ratio
. An application of Boltzmann’s principle then led Sackur to the conclusion
that the ratio
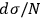 —and not
—and not
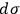 alone—is a universal constant. Sackur’s result contains a grain of truth in that it renders the entropy in his formula extensive.20 In his Wärmestrahlung, Planck started from extensivity and the law of the composition of probabilities to derive the Boltzmann principle (Planck 1906, 136–137). Apparently Sackur did not fully realize the significance of his own argument and result, but Planck did. Three years later, while struggling with the problem of making quantum entropy extensive, he would take up Sackur’s condition by stating that the elementary volume of the phase space of a gas depends on the number of molecules in the gas (Planck 1914, 9).
alone—is a universal constant. Sackur’s result contains a grain of truth in that it renders the entropy in his formula extensive.20 In his Wärmestrahlung, Planck started from extensivity and the law of the composition of probabilities to derive the Boltzmann principle (Planck 1906, 136–137). Apparently Sackur did not fully realize the significance of his own argument and result, but Planck did. Three years later, while struggling with the problem of making quantum entropy extensive, he would take up Sackur’s condition by stating that the elementary volume of the phase space of a gas depends on the number of molecules in the gas (Planck 1914, 9).
Sackur’s paper is representative of the general concerns of his work. As stated in the title, Sackur’s prime interest was the application of the methods developed by Planck in radiation theory to physical chemistry. Sackur followed Planck closely in the usage of probability and in handling the state space, but stopped short of explicitly introducing the quantum hypothesis. Instead, he attempted to clarify the properties of the elementary volume as a means to calculate theoretically the chemical constants. In the concluding section of the paper, he tested his procedure on the dissociation of iodine molecules and was able to retrieve the correct formula for the mass-action law.
3.5 The Generalization of Sackur’s Statistical Theory
Sackur’s focus on the burning issues of physical chemistry distracted his attention from the impact his method could have on quantum theory at large. Tetrode, whose work approached the problems of fledgling quantum statistics from a more abstract viewpoint, stressed the quantum interpretation of the elementary volume as well as the problem of extensivity right at the outset (Tetrode 1912).21 However, Sackur himself realized, in careful reconsideration, that his procedure suggested an intriguing perspective. He explored this viewpoint in a paper included in the Nernst Festschrift, published in May 1912.22 In that paper, the notion of the quantum of action and its application to the calculation of chemical constants appeared in the very title.
Sackur first tackled the problem of extensivity. He realized that the dependence of
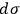 on the number of molecules was necessary to guarantee extensivity of the entropy function, but was no longer happy with the way it came about in his previous paper. At this point, Sackur was already convinced that the essence of the quantum hypothesis was probabilistic. As a consequence, he thought that a reconciliation of quantum theory with thermodynamics relied on a suitable definition of probability. To appreciate his procedure, we briefly summarize Sackur’s peculiar concept of probability.
on the number of molecules was necessary to guarantee extensivity of the entropy function, but was no longer happy with the way it came about in his previous paper. At this point, Sackur was already convinced that the essence of the quantum hypothesis was probabilistic. As a consequence, he thought that a reconciliation of quantum theory with thermodynamics relied on a suitable definition of probability. To appreciate his procedure, we briefly summarize Sackur’s peculiar concept of probability.
In 1911, Sackur defined the probability of a state as “the number that measures how many times a […] state […] is more probable than a state of the same energy and volume in which all atoms would have the same positions, directions and velocities” (Sackur 1911b, 959–960). This idiosyncratic definition, a result of Sackur’s personal reading of Planck and Boltzmann, led to the usual number of possible permutations of a state distribution. To retrieve extensivity, Sackur stated that the definition must be changed, and “we must resort […] to the concept of molecular disorder” (Sackur 1912a, 406). Once again, Sackur obtained this concept from the tradition of Planck and Boltzmann, but reinterpreted it in a peculiar way. In an arbitrary state, it is possible that more than one molecule occupies the same energy cell (or phase-space cell). If the state is perfectly disordered, each cell contains exactly one molecule. In other words, the molecules are spread throughout the available energy (or phase) space. This concept of molecular disorder could not be more distant from Planck’s and Boltzmann’s,23 but it accomplished its intended mission. As a result, Sackur modified the definition of probability as the ratio of the number of favorable cases to the number of possible cases, a proper fraction, and was again able to retrieve the term
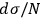 in the entropy formula, which guarantees its extensivity. This is yet another example of Sackur’s willingness to quite freely interpret the traditions of statistical mechanics to arrive at a concrete result.
in the entropy formula, which guarantees its extensivity. This is yet another example of Sackur’s willingness to quite freely interpret the traditions of statistical mechanics to arrive at a concrete result.
The second theoretical innovation introduced in the 1911 paper is the interpretation of the elementary volume in terms of Planck’s constant. Sackur kept the position-velocity space, but relied on Arnold Sommerfeld’s authority for interpreting the volume as
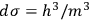 .24 This expression for the elementary volume enabled researchers “to calculate this quantity [i.e.,
.24 This expression for the elementary volume enabled researchers “to calculate this quantity [i.e.,
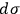 ] characteristic for the determination of the vapor pressure and of the chemical behavior without any experimental determination” (Sackur 1912a, 409).
] characteristic for the determination of the vapor pressure and of the chemical behavior without any experimental determination” (Sackur 1912a, 409).
The last part of the paper deals with the calculation of the chemical constants for mono- and polyatomic gases. Sackur displays his familiarity with the experimental data and his ability to work with them. Despite an incorrect expression for the rotational energy, Sackur obtained a reassuring agreement between his theoretical values and the experimental chemical constants, which suggested that his formula was correct.
In a subsequent paper (Sackur 1912b), Sackur’s shift toward an operational approach was complete; this paper was the most ambitious of his four articles on gaseous equilibria and statistical mechanics. He had apparently not believed that his prior probabilistic argument was satisfactory and thus sought to present a more general analysis. The striking feature of Sackur’s original approach based on the partitioning of the state space was that it resolved, with facility, the problem of the quantization of an aperiodic system. As we mention in the introduction, the quantum hypothesis was introduced to deal with periodic systems and expressed a relationship between the system’s energy and characteristic frequency. But there was no obvious way of ascribing a frequency to a gas. To circumvent this issue, Sackur worked on the state space of the system rather than the system itself—quantizing elementary regions instead of the system’s behavior. However, in his 1912 paper (Sackur 1912b) he changed tack. In accordance with his view that the quantum was intimately connected with probability, he endeavored to bring together the quantum hypothesis and classical probabilistic procedures used by kinetic theorists of the time. The result was a captivating argument with a nineteenth-century flavor.
The argument went as follows. Sackur first considers the case of a periodic system—a set of particles oscillating around an equilibrium point—which resembles an Einstein solid. There is no assumption about the nature of these particles except that, after a very long time, they take up all possible values of energy. Sackur then tackles the problem of calculating the probability that a particle has an energy between
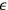 and
and
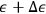 when it passes through the equilibrium point.25
Then he envisions a microscopic observer who can watch individual particles and send a signal every time a particle passes through the equilibrium point with the correct energy. As a result, the sought probability is given by the ratio of the number of signals,
when it passes through the equilibrium point.25
Then he envisions a microscopic observer who can watch individual particles and send a signal every time a particle passes through the equilibrium point with the correct energy. As a result, the sought probability is given by the ratio of the number of signals,
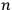 , to the total number of particles,
, to the total number of particles,
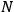 , that is,
, that is,
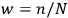 . This probability, Sackur states, is a function of energy and it is proportional to the width of the cell as well as to the span of time over which the observer watches the system,
. This probability, Sackur states, is a function of energy and it is proportional to the width of the cell as well as to the span of time over which the observer watches the system,
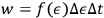 . Given that any value of energy is possible, Sackur insisted that it is a fundamental principle of probability calculus that if one waits long enough, all possible events will occur. This principle implies that if
. Given that any value of energy is possible, Sackur insisted that it is a fundamental principle of probability calculus that if one waits long enough, all possible events will occur. This principle implies that if
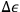 decreases, that is, the energy cells become smaller and more difficult to observe, the same probability can be maintained by extending the observation time
decreases, that is, the energy cells become smaller and more difficult to observe, the same probability can be maintained by extending the observation time
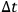 . In other words,
. In other words,
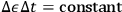 , a consequence that curiously resembles Heisenberg’s energy-time uncertainty relation.26
, a consequence that curiously resembles Heisenberg’s energy-time uncertainty relation.26
But if the observer is allowed to examine the system for an arbitrarily long time, he will count all the molecules infinitely many times, because they can assume all energy values over a long period. To ensure that each molecule is counted only once, the observation time must be set equal to the oscillation period,
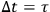 , in which case only molecules with energies
, in which case only molecules with energies
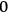 ,
,
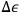 ,
,
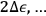 will be counted when
will be counted when
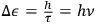 . The quantum hypothesis thereby affects the energy width
. The quantum hypothesis thereby affects the energy width
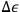 , that is to say the “experimental error” that the microscopic observer is allowed to make. The gist of Sackur’s probabilistic argument is that the quantum hypothesis is not necessarily a new physical assumption, but rather an “extension of the old statistical methods”:
, that is to say the “experimental error” that the microscopic observer is allowed to make. The gist of Sackur’s probabilistic argument is that the quantum hypothesis is not necessarily a new physical assumption, but rather an “extension of the old statistical methods”:
Contrary to the old picture developed by Planck for the derivation [of the equations of this theory], it [is] not necessary to assume an atomistic structure of energy or action. It suffice[s] to sharpen the (physical) concept of probability, namely by the almost obvious assumption that the verification of a result is the more probable, the longer one waits for it, and therefore even an extremely unlikely but possible result will have a finite probability to arise after an infinitely long time. (Sackur 1912b, 85)
Sackur further strived to show that the above quantum constraint emerges as soon as the probabilistic formalism is transformed into a physically workable procedure. The fictitious microscopic observer illustrates precisely this point. His attempt to demonstrate a continuity between the methods of classical statistical mechanics and quantum theory serves two related goals. First, it allows researchers to put aside some of the conundrums that came along with the quantum hypothesis. As the quotation above illustrates, Sackur was more eager to underscore the formal similarities between the classical and quantum approach than the weird consequences stemming from discontinuity and discretization. Second, the above similarities justified in Sackur’s eyes the application of the quantum procedure to the problems left open by classical theory. Precisely because the quantum hypothesis appeared to him as an extension of statistical mechanics, he expected it to fill the remaining gaps in the thermodynamic and statistico-mechanical treatments of chemical phenomena.
Sackur then tests his probabilistic argument by retrieving Planck’s black-body radiation law and Einstein’s formula for the heat capacity of solids at low temperatures. In this connection, Sackur makes an interesting comment, namely that in the limit of high temperatures, one obtains the Rayleigh-Jeans formula and the Dulong-Petit law for the two above cases, respectively. Then he points out for the case of the Rayleigh-Jeans formula that it is to be regarded not as a purely classical result but rather an approximate quantum result.
So much for periodic systems. For aperiodic systems, the maximization of entropy proceeds formally in the same way as for periodic ones, except that one has to identify a proper substitute for the characteristic frequency
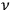 . Sackur argues that the limitation imposed by the observation time must be such that the velocity of the molecule be constant during that time: “we have to choose the observation time […] so that during
. Sackur argues that the limitation imposed by the observation time must be such that the velocity of the molecule be constant during that time: “we have to choose the observation time […] so that during
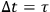 the molecule experiences no change of velocity, that is no collision” (Sackur 1912b, 75–76). Sackur is apparently referring to the mean time that the molecule spends to cover the mean free path. In that span of time, the molecules maintain their velocity and the observer will count only those molecules which are in a given energy cell.27
the molecule experiences no change of velocity, that is no collision” (Sackur 1912b, 75–76). Sackur is apparently referring to the mean time that the molecule spends to cover the mean free path. In that span of time, the molecules maintain their velocity and the observer will count only those molecules which are in a given energy cell.27
To ensure extensivity, Sackur resorted to defining the three components of velocity as the ratio between the corresponding mean free paths and the mean free times. Since the mean free path depends on the number of molecules, this procedure surreptitiously introduces the same dependence as the definition of the elementary cell in the position-velocity space. In effect, Sackur treated the gas as if it consisted of molecules distributed into
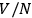 independent sub-volumes defined by the mean free path.
independent sub-volumes defined by the mean free path.
Next, Sackur wrote down his final entropy formula for a monoatomic ideal gas, after filing three other versions in his preceding papers,
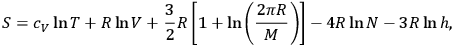
|
3.13 |
where
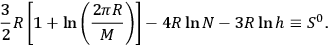
|
3.14 |
In the last section of his paper, Sackur extended this approach to polyatomic gases. The classical treatment of the rotational energy he presented contained an error, which Tetrode pointed out to him in a personal letter. Sackur responded by publishing a paper dedicated to the discussion of gaseous molecules with two or three atoms, in which he corrected this error (Sackur 1912c).28
By the end of 1912, Sackur considered his quantum theory of gaseous equilibrium to be complete: he had calculated the chemical constants for a variety of gases, which was his initial stated goal. His contact with Fritz Haber and Haber’s Kaiser Wilhelm Institut enticed him to work on applications of quantum theory to other physico-chemical problems, such as the behavior of gases at very low temperatures (Sackur 1914).29 This topic preoccupied him during the last, Berlin phase of his career.
3.6 Conclusion
The Sackur-Tetrode equation is perhaps the most lasting of Sackur’s contributions to quantum theory and, indeed, to science. It is still presented in textbooks as the quantum expression for the translational entropy of a monoatomic gas at high temperatures and low densities. Like Nernst’s heat theorem, it played an important part in the collective groping that led eventually to a complete theory of quantum gases. Sackur’s scientific ontogenesis provides a clue about the phylogenesis of his contemporaries. Although Sackur’s theoretical rendition of the chemical constants was immediately and widely accepted as a touchstone of thermochemistry, his general theoretical reflections did not have the same fate. Vacillations between phase space and microscopic observers, between discontinuity and probabilistic arguments, that is, between tradition and innovation still reveal deep uncertainties concerning the basis on which his computational results were founded.
Some of his ideas were subsequently adopted or discussed—for instance, the
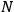 dependence of the elementary cell or the division of the gas volume into
dependence of the elementary cell or the division of the gas volume into
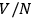 subvolumes to ensure extensivity. But nobody seems to have followed his suggestion for a purely probabilistic-operational foundation of the quantum hypothesis. Physicists and physical chemists favored Otto Stern’s approach based on the vapor-solid equilibrium (Stern 1913; 1919), which eventually triggered Enrico Fermi’s analysis of the statistics of identical particles (1919).
subvolumes to ensure extensivity. But nobody seems to have followed his suggestion for a purely probabilistic-operational foundation of the quantum hypothesis. Physicists and physical chemists favored Otto Stern’s approach based on the vapor-solid equilibrium (Stern 1913; 1919), which eventually triggered Enrico Fermi’s analysis of the statistics of identical particles (1919).
However, reducing Sackur’s case to a story about which aspects of his work succeeded and which failed to have an impact would mean to miss more interesting historiographical points. We conclude with two reflections on Sackur and the complex landscape of the quantum physics in the 1910s that he helped shape.
First, Sackur was a member of the diverse and variegated scientific community that developed quantum physics. In the 1910s, the quantum hypothesis made its way into statistical mechanics, radiation theory, spectroscopy, theory of matter, physical chemistry and atomic modeling. In such a complex landscape, the sheer multitude of the specialists involved lent the contentions about the quantum a considerable polyphony but little harmony. Although formal tools and mathematical techniques were widely shared among more famous (such as Einstein, Planck, or Nernst) and relatively unknown (such as Tetrode, or Sackur himself) players, the quantum hypothesis meant different things to different people. For instance, Einstein’s perspective, shaped mostly by his interest in radiation theory, differed greatly from Nernst’s, which depended on his desire to establish the validity of the heat theorem. In our case, Sackur’s background in physical chemistry was key to shaping his interpretation of the quantum. Eager to put the quantum to the service of long-standing problems of thermochemistry—as well as to impress a potential employer—Sackur stressed the continuity between classical statistical techniques and the quantum. The variety of approaches made the 1910s an interesting period both from historiographical and epistemological points of view.
Second, Sackur belonged to a part of the physics community whose research style was quite different from that of, say, Planck, Einstein or Bohr. Sackur’s research was not driven by an adherence to strong principles, as he lacked a grand methodological guidance such as Planck’s concept of absolute entropy. This difference echoes Suman Seth’s recent distinction between “physics of principle” and “physics of problems” (Seth 2010). Sackur was, no doubt, more sympathetic to an approach of starting from and returning to concrete problems. The state of flux in which quantum physics found itself at the beginning of the 1910s facilitated and almost encouraged problem-oriented lines of attack. Thus, Sackur’s was, so to speak, a “mundane” quantum physics coming “from below” as a result of his personal understanding of abstract concepts and of his pragmatic agenda. Although curious about the wider implications of his arguments, he remained largely unconcerned about the quantum formalism and, in the end, settled on a conservative position, according to which the quantum is an extension of classical statistical mechanics. For a vast majority of Sackur’s peers—who eventually provided a lasting contribution—the quantum was mainly a tool. For them, as for Sackur, quantum physics made sense when viewed in the context of well-defined problems in classical physics that arose within the framework of their own disciplines.30
References
Abegg, Richard, Otto Sackur (1909). Physikalisch-Chemische Rechenaufgaben. Leipzig: Barth.
Arrhenius, Svante (1910). Richard Abegg. Zeitschrift für Elektrochemie und angewandte physikalische Chemie 16: 554-557
Auerbach, Friedrich (1915). Otto Sackur – Nekrologe. Jahresbericht der Schlesischen Gesellschaft für Vaterländische Kultur 1: 35-37
Badino, Massimiliano (2009). The Odd Couple: Boltzmann, Planck and the Application of Statistics to Physics (1900–1913). Annalen der Physik 18: 81-101
- (2013). Dissolving the Boundaries Between Research and Pedagogy: Otto Sackur's . In: Research and Pedagogy. A History of Quantum Physics through Its Textbooks Ed. by Massimiliano Badino, Jaume Navarro.
Bartel, Hans-George, Rudolf Hübener (2007). Walther Nernst, Pioneer of Physics and of Chemistry. Singapore: World Scientific Publishing.
Bohr, Niels (1923). Anwendung der Quantentheorie auf den Atombau. I. Die Grundpostulate der Quantentheorie. Zeitschrift für Physik 13: 117-165
Coffey, Patrick (2006). Chemical Free Energies and the Third Law of Thermodynamics. Historical Studies in the Physical and Biological Sciences 36: 365-396
Darrigol, Olivier (1988). Statistics and Combinatorics in Early Quantum Theory. Historical Studies in the Physical and Biological Sciences 19: 17-80
- (1991). Statistics and Combinatorics in Early Quantum Theory, II: Early Symptoma of Indistinguishability and Holism. Historical Studies in the Physical and Biological Sciences 21: 237-298
Des Coudres, Theodor (1910). Richard Abegg. Physikalische Zeitschrift 11: 425-429
Desalvo, Agostino (1992). From the Chemical Constant to Quantum Statistics: A Thermodynamic Route to Quantum Mechanics. Physis 29: 465-537
Einstein, Albert (1907). Die Plancksche Theorie der Strahlung und die Theorie der spezifischen Wärme. Annalen der Physik 22: 180-190
Eucken, Arnold (1912). Die Molekularwärme des Wasserstoffs bei tiefen Temperaturen. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin
- (1914). Die Entwicklung der Quantentheorie vom Herbst 1911 bis Sommer 1913. In: Die Theorie der Strahlung und der Quanten Ed. by Arnold Eucken. Halle: Knapp 371-405
- (1922). Der Nernstsche Wärmeersatz. Ergebnisse der exakten Naturwissenschaften 1: 120-162
Fermi, Enrico (1923). Sopra la teoria di Stern della costante assoluta dell'entropia di un gas perfetto monoatomico. Rendiconti della Accademia dei Lincei 32: 395-398
Friedrich, Bretislav, Dudley Herschbach (2003). Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics. Physics Today 56(12): 53-59
Gearhart, Clayton A. (2010). `Astonishing Successes' and `Bitter Disappointment': The Specific Heat of Hydrogen in Quantum Theory. Archive for History of Exact Sciences 64: 113-202
Gibbs, Josiah Willard (1878). On the Equilibrium of Heterogeneous Substances. Transactions of the Connecticut Academy 3: 108-248
Guldberg, Cato M., Peter Waage (1899). Untersuchungen über die chemischen Affinitäten. Abhandlungen aus den Jahren 1864, 1867, 1879. Leipzig: Englemann.
Haber, Fritz (1905). Thermodynamik technischer Gasreaktionen. Munich: Oldenbourg Verlag.
von Helmholtz, Hermann (1882). Die Thermodynamik chemischer Vorgänge. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin 1: 22-39
Hertz, Walther (1915). Otto Sackur. Physikalische Zeitschrift 16: 113-115
Hiebert, Edwin N. (1971). The Energetic Controversy and the New Thermodynamics. In: Perspectives in the History of Science and Technology Ed. by Duhane H. D. Roller. Normal: University of Oklahoma Press 67-86
- (1983). Walther Nernst and the Application of Physics to Chemistry. In: Springs of Scientific Creativity Ed. by Rutherford Aris, Howard T. Davis, H.T. D.. Minneapolis: University of Minnesota Press 203-231
Hoyer, Ulrich (1980). Von Boltzmann zu Planck. Archive for History of Exact Sciences 23: 47-86
Jüttner, Ferenz (1911). Über die Ableitung der Nernstschen Formeln für Reaktionen in kondensierten Systemen. Zeitschrift für Elektrochemie und angewandte physikalische Chemie 17: 139-143
Kipnis, Alexander (2005). Entry on Otto Sackur. In: Neue Deutsche Biographie Berlin: Dunker und Humblot 344
Koref, Fritz (1911). Messungen der spezifischen Wärme bei tiefen Temperaturen mit dem Kupferkalorimeter. Annalen der Physik 36: 49-73
Kormos Barkan, Diana (1999). Walther Nernst and the Transition to Modern Physical Science. Cambridge: Cambridge University Press.
Kox, Anne J. (2006). Confusion and Clarification: Albert Einstein and Walther Nernst's Heat Theorem, 1911–1916. Studies in History and Philosophy of Modern Physics 37: 101-114
Morse, Philip M. (1969). Thermal Physics. Reading: The Benjamin/Cumings Publishing Company.
Nernst, Walther (1906a). Über die Berechnung chemischer Gleichgewichte aus thermischen Messungen. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen 1: 1-39
- (1906b). Über die Beziehungen zwischen Wärmeentwicklung und maximaler Arbeit bei kondensierten Systemen. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin
- (1907). Experimental and Theoretical Applications of Thermodynamics to Chemistry. New Haven: Yale University Press.
- (1911). Zur Theorie der spezifischen Wärme und über die Anwendung der Lehre von den Energiequanten auf physikalisch-chemische Fragen überhaupt. Zeitschrift für Elektrochemie und angewandte physikalische Chemie 17: 265-275
- (1917). Die theoretischen und experimentellen Grundlagen des neuen Wärmesatzes. Halle: Knapp.
Pick, Hans (1915). Otto Sackur. Chemiker Zeitung 39: 13
Pier, Mathias (1909). Spezifische Wärme von Gasen bei sehr hohen Temperaturen. Zeitschrift für Elektrochemie 15: 536-540
- (1910). Spezifische Wärme und Gasgleichgewicht nach Explosionsversuchen. Zeitschrift für Elektrochemie 16: 897-903
Planck, Max (1906). Vorlesungen über die Theorie der Wärmestrahlung. Leipzig: Barth.
- (1911). Vorlesungen über die Thermodynamik. Leipzig: Veit.
- (1913). Vorlesungen über die Theorie der Wärmestrahlung. Leipzig: Barth.
- (1914). Die gegenwärtige Bedeutung der Quantenhypothese für die kinetische Gastheorie. In: Vorträge über die kinetische Theorie der Materie und der Elektrizität Ed. by David Hilbert. Göttingen: B. G. Teubner 3-16
Polanyi, Michael (1913). Eine neue thermodynamische Folgerung aus der Quantenhypothese. Verhandlungen der Deutschen Physikalischen Gesellschaft 15: 156-161
Rasetti, Franco (1924). La costante assoluta dell'entropia e le sue applicazioni. Il nuovo cimento 3: 67-86
Sackur, Otto (1911a). Zur kinetischen Begründung des Nernstschen Wärmetheorems. Annalen der Physik 34: 455-468
- (1911b). Die Anwendung der kinetischen Theorie der Gase auf chemische Probleme. Annalen der Physik 36: 958-980
- (1912a). Die Bedeutung des elementaren Wirkungsquantums für die Gastheorie und die Berechnung der chemischen Konstanten. Halle: Knapp.
- (1912b). Die universelle Bedeutung des sogenannten elementaren Wirkungsquantums. Annalen der Physik 40: 67-86
- (1912c). Die `Chemischen Konstanten' der zwei- und dreiatomigen Gase. Annalen der Physik 40: 87-106
- (1914). Die Zustandsgleichung der Gase und die Quantentheorie. Zeitschrift für Elektrochemie und angewandte physikalische Chemie 20: 563-570
Seth, Suman (2010). Crafting the Quantum: Arnold Sommerfeld and the Practice of Theory, 1890–1926. Boston: MIT Press.
Sommerfeld, Arnold (1911). Das Plancksche Wirkungswachstum und seine allgemeine Bedeutung für die Molekularphysik. Physikalische Zeitschrift 12: 1057-1068
- (1914). Probleme der freien Weglänge. In: Vorträge über die kinetische Theorie der Materie und der Elektrizität Ed. by David Hilbert. Göttingen: B. G. Teubner 125-166
Stern, Otto (1913). Zur kinetischen Theorie des Dampfdrucks einatomiger fester Stoffe und über die Entropiekonstante einatomiger Gase. Physikalische Zeitschrift 14: 629-632
- (1919). Zusammenfassender Bericht über die Molekulartheorie des Dampfdruckes fester Stoffe und ihre Bedeutung für die Berechnung chemischer Konstanten. Zeitschrift für Elektrochemie 25: 66-80
Tetrode, Hugo M. (1912). Die chemische Konstante der Gase und das elementare Wirkungsquantum. Annalen der Physik 38: 434-442
Van Delft, Heike (2007). Freezing Physics. Heike Kamerlingh Onnes and the Quest for Cold. Amsterdam: Koninklijke Nederlandse Akademie van Wetenschappen.
Van ' t Hoff, Jacobus (1886). L'équilibre chimique dans les systèmes gazeux, ou dissous à l'état dilué. Archives néerlandaises des sciences exactes et naturelles 20: 239-302
Footnotes
On this point see (Gearhart 2010).
Mentions of Sackur’s work can be found in (Darrigol 1991; Desalvo 1992).
There are only few sources available about Sackur’s life. Here we have especially relied on (Kipnis 2005) and obituaries written by colleagues and friends (Kipnis 2005).
In Tessin, near Rostock (Arrhenius 1910; Des Coudres 1910).
During this period, Otto Stern earned his doctorate under Sackur’s supervision, on osmotic pressure of “generalized soda-water,” a topic of his own choice (Friedrich and Herschbach 2003). Also, it was Sackur who, using Fritz Haber’s mediation, helped Stern find his post-doctoral position with Einstein in 1912 (Kuhn 1962). On Sackur’s pedagogical activity see (Badino 2013).
A collection of Guldberg and Waage’s publications on the topic was published in the series Ostwald Klassiker der Exakten Wissenschaften in a translation by Abegg (1899).
For the technique used to solve this equation see (Haber 1905, 22–23).
For theoretical and experimental aspects of physical chemistry at the end of the nineteenth century, see (Hiebert 1971; 1983; Kormos Barkan 1999; Coffey 2006).
Julius Thomsen (1826–1909) in 1852 and Marcellin Berthelot (1827–1907) in 1869 speculated on the behavior of chemical reactions in the vicinity of absolute zero. See (Coffey 2006). For Nernst’s personal take on the story, see the opening chapter of (Nernst 1917).
Namely to zero, i.e.,
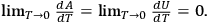
For a modern treatment, see (Morse 1969, 143–145).
For a thorough presentation of the issue, see (Nernst 1907; 1917).
Although Nernst was reluctant to commit his conviction to paper, there are at least two pieces of indirect evidence: First, in about 1910 Nernst attempted to prove his theorem on the grounds of a purely thermodynamic argument independent of the nature of the substances involved (Kox 2006); second, after 1906 he put his Berlin group to work on the measurement of the specific heats of gases. Before the Solvay Conference, Nernst supervised three doctoral dissertations on the specific heats of gases—by Frank Voller (1908), Friedrich Keutel (1910), and Robert Thibaut (1910). At the same time, Mathias Pier worked on the measurement of specific heats at high temperatures (Pier 1909; 1910), while Fritz Koref and Eucken concentrated on low temperatures (1910).
From Physikalische Zeitschrift and Zeitschrift für Elektrochemie it can be established that Sackur attended the meetings of the Bunsen Society for Physical Chemistry from 1906 until 1914, the year of his death. In 1908, he also reported about the meeting for Physikalische Zeitschrift.
Attempts along a similar direction were (Sackur 1911a).
Planck dwelled on the concept of absolute entropy both in the third edition of his Thermodynamik and in the second edition of the Wärmestrahlung (Planck 1911; 1913).
On one hand, the applicability of the Stirling formula relies on the assumption that the elementary regions are large enough to contain many molecules. On the other hand, replacing summations by integration requires the regions to be infinitesimal. Classical kinetic theory hinges upon the balance between these two contravening requirements, see also (Hoyer 1980; Darrigol 1988). We discuss Sackur’s reflections on it in the next section.
To a modern reader, Sackur’s talk about a tendency of molecules to clump in phase regions may suggest some, albeit naive, anticipation of quantum statistics (Darrigol 1991). However, the main problem that quantum statistics had to deal with, namely the extensivity of entropy, was not considered. And when the problem came up, Sackur did not seem to recognize it as a fundamental issue.
From this argument, one may discern another source of inspiration in Sackur’s work, for it closely resembles the 1905 light-quantum paper, in which Einstein compares the probabilities for a gas to be in a given volume and in a part of that same volume.
If
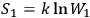 and
and
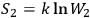 are the entropies of two subsystems, and
are the entropies of two subsystems, and
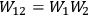 is the probability of the composed system, then
is the probability of the composed system, then
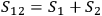 .
.
For a discussion of Tetrode’s paper, see (Darrigol 1991; Desalvo 1992).
The paper (Sackur 1912a) is dated March 1912. Since Tetrode’s article was also published in March, it seems that Sackur worked out the consequences of his approach independently.
Boltzmann considered molecular disorder to be the condition for applying probability in gas theory, while Planck was convinced that disorder had the power to eliminate any violation of the second law of thermodynamics. For a discussion of these two views, see (Badino 2009).
Sommerfeld proposed the interpretation of the elementary volume in terms of
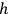 as a general quantization condition for a periodic system at the First Solvay Conference and in a widely discussed paper (Sommerfeld 1911).
as a general quantization condition for a periodic system at the First Solvay Conference and in a widely discussed paper (Sommerfeld 1911).
The argument could be carried out for any point of oscillation, but Sackur chooses the equilibrium point since there the energy of the particle is purely kinetic.
The energy-time uncertainty relation has a more genuine predecessor in the work of Niels Bohr (1923, 150).
Sackur’s idea of using the mean free path as a parameter to quantize the gas was adopted the following year by Sommerfeld and his collaborator Wilhelm Lenz (Sommerfeld 1914).
Although Tetrode’s letter to Sackur has been lost, we know about its existence from a footnote in Sackur’s (1912b) paper.
Because of his intention to move on to the experimental determination of the gas law at very low temperatures, Sackur applied for a position in Kamerlingh Onnes’s institute in Leiden. However, Onnes dismissed his application with scorn (Van Delft 2007, 477).
Massimiliano Badino and Bretislav Friedrich have contributed equally to this paper.

