Chapter structure
- 2.1 The Classical Theory of Optical Dispersion
- 2.2 Bohr’s Model of the Atom and the Optical
Dispersion of Molecules - 2.3 Debye and the First Theory of Optical Dispersion According to Bohr’s Model
- 2.4 Sommerfeld and Optical Dispersion in 1915
- 2.5 Reactions to Debye-Sommerfeld’s Hybrid Theory
- 2.6 Sommerfeld’s Counterattack
- 2.7 From the Hybrid Theory to the Light Quantum
- 2.8 A New Thread of the Story
- 2.9 Conclusion
- Abbreviations and Archives
- Acknowledgements
- References
- Footnotes
This paper describes one significant episode in the transition between classical and quantum theories. It analyzes the first theory of optical dispersion that ensued from the extension of Niels Bohr’s quantum model of the atom to other optical phenomena outside of spectroscopy. This theory was initially developed by Peter Debye in 1915 and then was endorsed and extended by Arnold Sommerfeld in 1915 and 1917. The most interesting aspect of the Debye-Sommerfeld theory for the present paper is that it clearly typifies important features of debates concerning the boundaries between classical and quantum physics, focusing on the period from 1913 to the early 1920s.
Optical dispersion consisted of splitting white light into different colors because of its change of velocity when passing through a transparent, prismatic medium. From the 1870s onward, it was well known that light was continuously dispersed across the entire spectrum, except at those specific frequencies, characteristic of the medium, at which light was completely absorbed. In other words, dispersion and absorption of light were complementary phenomena. From 1872, this behavior was explained using one enduring theoretical representation: the Mitschwingungen model. This model pictured the interaction between light and matter as a continuous process of interaction between waves and particles performing induced vibrations, called Mitschwingungen.
In 1913, this model conflicted with certain aspects of Bohr’s quantum model of the atom. Contrary to the Mitschwingungen model, Bohr envisioned the exchange of energy between light and matter as a discrete process, mediated by the emission or absorption of quanta of energy.
Debye and Sommerfeld’s theories were the first attempts at combining optical dispersion with the new atomic model. To do so, both physicists had to come to terms with whether optical dispersion could still be considered a classical process, even in the context of Bohr’s model, or had to be reinterpreted as a quantum phenomenon, in the same fashion as spectral lines.
Debye and Sommerfeld decidedly followed the first path in 1915. They borrowed various elements of the classical Mitschwingung theories and embedded them into Bohr’s model. Most importantly, Sommerfeld saw a clear confirmation in the new theory of optical dispersion that quantum and classical physics could coexist without causing inconsistencies. Hence from 1915 to 1917, he defended it, despite skeptical and critical responses. In so doing, Sommerfeld defined a divide between two domains of physics: optical dispersion as a central example of classical physics and spectroscopy as the central phenomenon of quantum physics.
In the 1920s, Sommerfeld’s theory could no longer withstand certain criticisms addressing this divide. Optical dispersion had to be regarded as a pure quantum phenomenon. This aroused the question of accounting for its continuous features in quantum terms, so well-explained by the classical model of Mitschwingungen. This search for a quantum explanation of optical dispersion brought about a renegotiation of quantum concepts and techniques according to different strategies from the 1921 onward, most importantly in Sommerfeld’s school in Munich and in Bohr’s school in Copenhagen.
In this paper, I follow the development of this intricate story from 1913 through the early 1920s, focusing particularly on Sommerfeld’s intervention in the debate. In the first section, I summarize the main aspects of the classical theory of optical dispersion developed from the 1870s until 1913. I deal with Bohr’s model of the atom in section 2. In sections 3 and 4, I describe at length Debye and Sommerfeld’s theory. Then in section 5, I detail the extensions, comments and criticisms of the theory; and in the following section, I tackle Sommerfeld’s strategies to counter them. Sommerfeld’s last words on the theory are addressed in section 7. In section 8, I discuss a new direction in the debate about classical versus quantum optical dispersion. Finally, I conclude with a short introduction to the quantum theories of optical dispersion that emerged in the 1920s.
2.1 The Classical Theory of Optical Dispersion
2.1.1 Microphysics and Electromagnetic Theory
In the 1870s, some peculiar features of optical dispersion, a phenomenon recognized as early as the 17th century, were discovered. In particular, the frequency dependence of the velocity of light (and as a result, its direction) was continuous across the range of the spectrum, except at those frequencies where light was absorbed by the dispersing material.
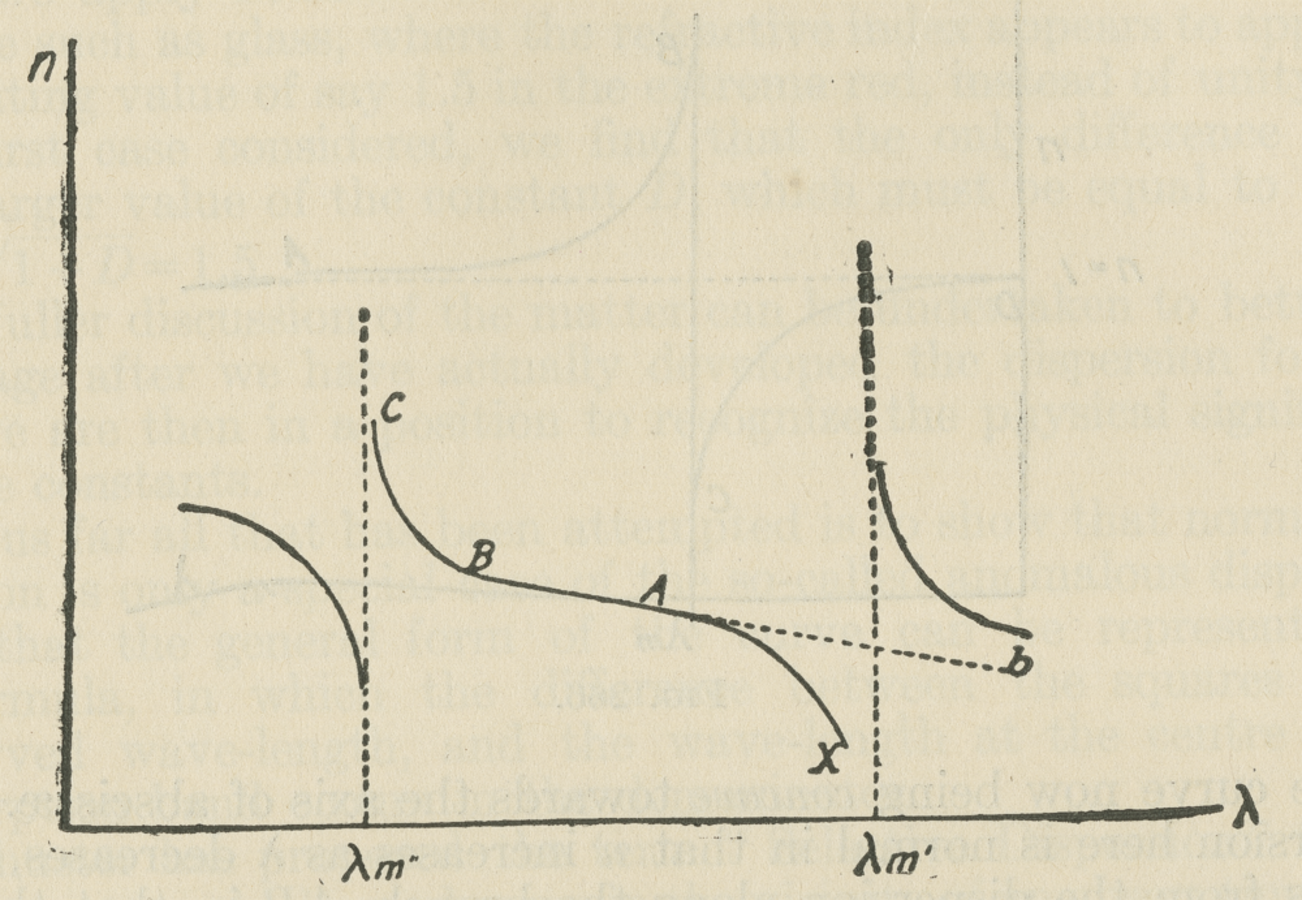
Fig. 2.1: Graphic representation of the index of refraction as a function of the wavelength of light (Wood 1904, 377).
As shown in fig. (2.1), in the neighborhood of the absorbed frequency, the index of refraction increases asymptotically as one approaches the singularity from the right (region C–B), and it decreases asymptotically as one approaches from the left (region A–X). This was dubbed “anomalous dispersion.” This phenomenon was first discovered by Christian Christiansen and then thoroughly investigated for liquids by August Kundt during 1870–1872 (Christiansen 1870; Kundt 1870; 1871a; 1871b; 1872). Then Robert Wood in 1904, Rudolf Ladenburg (in collaboration with Loria) in 1908, and P. V. Bevan in 1910 provided a quantitative description for various gases (Wood 1904; Ladenburg and Loria 1908; Bevan 1910). The region B–A in fig. (2.1) corresponds to normal dispersion as observed since Newton’s time.
As previously mentioned, at least as early as 1872 physicists represented these features using a specific model of interaction between microscopical particles and light waves: the Mitschwingungen model (Sellmeier 1872a; 1872b; 1872c; 1872d; von Helmholtz 1875; discussed in Buchwald 1985; Whittaker 1910). According to this model, when light impinged on matter, particles and light waves oscillated together so that the dispersed light stemmed from the entangled waves induced by matter oscillations and primary waves. This approach was radically different from all earlier explanations of optical dispersion. Previously, matter could only modify the propagation of light, without contributing to its generation.
More specifically, according to the Mitschwingungen model, particles were quasi-elastically bound to their equilibrium positions, which led to their having characteristic proper frequencies of vibration. When light interacted with these particles, it caused a forced oscillation, which was assumed to be the cause of the emission of a secondary set of waves, having the same frequency as the original light, but delayed by a phase factor. The primary light and the secondary radiation were presumed to interfere, and thus form new waves with different phase velocities depending on the frequency of the light
 . This yielded the following equation for the index of refraction (that is the ratio between the velocity of light in the medium and the velocity of light in vacuum):
. This yielded the following equation for the index of refraction (that is the ratio between the velocity of light in the medium and the velocity of light in vacuum):
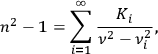
|
2.1 |
where each term of the summation corresponds to one possible proper frequency of the dispersing matter. However, if the incoming light had the same frequency as the proper frequency of any of the particles (
 ), the light was entirely absorbed by the matter, without any emission of secondary waves. In such a case, the light and matter came into resonance.
), the light was entirely absorbed by the matter, without any emission of secondary waves. In such a case, the light and matter came into resonance.
The phenomenon of optical dispersion was thus defined by two parameters, the proper frequency
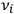 and the constant
and the constant
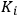 , which somehow played the role of an “intensity” of dispersion. Both parameters could be calculated a posteriori by fitting experimental data into the above formula.
, which somehow played the role of an “intensity” of dispersion. Both parameters could be calculated a posteriori by fitting experimental data into the above formula.
The essence of this microscopic mechanism of matter interacting with light remained unchanged for over fifty years, although physicists would embed it into different frameworks. With the establishment of the electromagnetic theory of light, particles came to be considered vibrating charges. According to the electromagnetic version of the model, the vibration of these charges induced a periodic polarization of the medium, which in turn caused secondary waves to be emitted (Glazebrook 1886; von Helmholtz 1892; Drude 1894; 1900; Voigt 1899; 1901).
2.1.2 Optical Theory and the Structure of Matter
Paul Drude systematized the electromagnetic approach to optical dispersion in two editions of his Lehrbuch der Optik (Drude 1900) as well as in his research papers (Drude 1904a; 1904b). In these works, Drude established an extremely fruitful connection between optics and the physico-chemical properties of matter. His approach relied on two fundamental steps. First, he suggested that the charged particles involved in dispersion were in fact the recently discovered electrons, characterized by the ratio
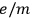 , first measured by Emil Wiechert and Joseph Thomson in 1897. In 1904, Drude took up the value of this ratio
, first measured by Emil Wiechert and Joseph Thomson in 1897. In 1904, Drude took up the value of this ratio
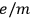 and, by assuming that
and, by assuming that
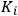 was proportional to the number of optical electrons
was proportional to the number of optical electrons
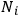 with proper frequency
with proper frequency
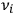 , obtained
, obtained
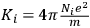 .1 This gave the following expression for the index of refraction:
.1 This gave the following expression for the index of refraction:
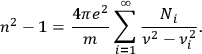
|
2.2 |
The number
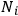 was called the number of “dispersion electrons” thereafter. This definition of
was called the number of “dispersion electrons” thereafter. This definition of
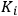 led to optical dispersion becoming a very powerful tool to investigate the microphysical structure of matter.
led to optical dispersion becoming a very powerful tool to investigate the microphysical structure of matter.
Drude’s second step was to suggest that the electrons responsible for dispersion were the so-called valence electrons. This proposal was far from obvious. It was not until 1904 that chemical valence was connected to electron theory. Richard Abegg suggested that the valence number corresponded to the number of electrons loosely attached to an atom and having the tendency to migrate from one atom to another to form molecules (Abegg 1904). In taking up Abegg’s suggestion, Drude extended the boundaries of the concept of electronic valence from physical chemistry to the rapidly-growing field of applications of the electron theory to optics. This added a molecular dimension to the problem of optical dispersion and suggested its use as a tool for exploring the properties of the periodic table.
The identification of dispersion electrons with valence electrons was problematic. In some cases, see for example the work of Clive and Maude Cuthbertson (1910) and John Koch (1913), some slight discrepancies were found for normal dispersion in gaseous molecular hydrogen, helium, oxygen and nitrogen. More specifically, the number of dispersion electrons
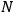 calculated by fitting the experimental data using eq. (2.2) was only two-thirds of the number of valence electrons of these gases. The situation was more serious for anomalous dispersion in vapors of sodium, potassium and monoatomic hydrogen, where the discrepancies were larger by orders of magnitude (Wood 1904; Ladenburg and Loria 1908; Bevan 1910). However, the Mitschwingung mechanism of light-matter interaction was not affected by these inconsistencies. The relation between dispersion and valence electrons only affected issues at the border between physics and chemistry and not the more general mechanical model.
calculated by fitting the experimental data using eq. (2.2) was only two-thirds of the number of valence electrons of these gases. The situation was more serious for anomalous dispersion in vapors of sodium, potassium and monoatomic hydrogen, where the discrepancies were larger by orders of magnitude (Wood 1904; Ladenburg and Loria 1908; Bevan 1910). However, the Mitschwingung mechanism of light-matter interaction was not affected by these inconsistencies. The relation between dispersion and valence electrons only affected issues at the border between physics and chemistry and not the more general mechanical model.
2.2 Bohr’s Model of the Atom and the Optical
Dispersion of Molecules
In 1913, a new element entered the story: Bohr’s quantum model of the atom. In the series of papers he published that year (Bohr 1913a; 1913b; 1913c), Bohr assumed new laws of atomic stability derived from the introduction of a single parameter that was completely foreign to classical electrodynamics: Planck’s elementary quantum of action
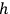 . Bohr’s model was defined by the way matter absorbed or emitted quanta of light of energy
. Bohr’s model was defined by the way matter absorbed or emitted quanta of light of energy
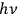 .
.
Bohr postulated that orbiting electrons maintained constant trajectories, which were mechanically stable and on which they did not radiate. Emission and absorption of energy only took place when the electrons jumped from one orbit to another. In the new theory, the frequency
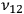 of the radiation absorbed or emitted was related to the energies
of the radiation absorbed or emitted was related to the energies
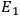 and
and
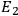 of the orbits or levels through the relation
of the orbits or levels through the relation
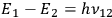 . With this novel redefinition of the exchange of energy between matter and light, Bohr broke the classical link between the absorption/emission frequency of radiation and the mechanical frequency of the vibrating electron that was at the root of the Mitschwingungen model.
. With this novel redefinition of the exchange of energy between matter and light, Bohr broke the classical link between the absorption/emission frequency of radiation and the mechanical frequency of the vibrating electron that was at the root of the Mitschwingungen model.
Bohr supported his model by applying these postulates to monoatomic hydrogen, where he found an excellent agreement between the frequencies
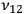 and the spectral lines of the Balmer series. In addition to this simple case, in the second and third part of the trilogy, Bohr addressed at length the constitution and stability of more complex atomic systems and molecules. To fix the conditions of stability for electron orbits, Bohr introduced another postulate: the angular momentum along a stationary orbit must remain constant.
and the spectral lines of the Balmer series. In addition to this simple case, in the second and third part of the trilogy, Bohr addressed at length the constitution and stability of more complex atomic systems and molecules. To fix the conditions of stability for electron orbits, Bohr introduced another postulate: the angular momentum along a stationary orbit must remain constant.
The quantized nature of the angular momentum imposed severe restrictions on the stability of the systems under the action of external forces since it allowed only two possible modifications of the orbits. Within the same plane of the orbit, changes could only occur by quantum jumps corresponding to changes in energy of value
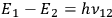 . Perpendicular to the plane of the orbit, trajectories could undergo small periodic variations, but only if the radius remained unchanged, thus preserving the constancy of angular momentum. The frequency of such small variations could be computed using the tools of ordinary mechanics.
. Perpendicular to the plane of the orbit, trajectories could undergo small periodic variations, but only if the radius remained unchanged, thus preserving the constancy of angular momentum. The frequency of such small variations could be computed using the tools of ordinary mechanics.
This division into two separate mechanisms mirrored a distinction that Bohr introduced in his trilogy between the “true emission of light” and the “scattering of light.” Bohr employed this dichotomy to characterize the ordinary line-spectra of atomic hydrogen (“true emission of light,” following quantum rules) and the lines of the coronal spectrum of the sun discussed by John W. Nicholson in 1912 (“scattering of light,” ruled by classical mechanics) (Bohr 1913a, 23–24). In addition, he relied on this distinction in the context of optical dispersion, since he presumed that this phenomenon was also caused by mechanical perturbations of orbits:
The ordinary mechanics can be used in calculating the vibrations of the electrons perpendicular to the plane of the ring—contrary to the case of vibrations in the plane of the ring. This assumption is supported by the apparent agreement with observations obtained by Nicholson in his theory of the origin of lines in the spectra of the solar corona and stellar nebulae. In addition it will be shown later that the assumption seems to be in agreement with experiments on dispersion. (Bohr 1913b, 482)
In the second and third part of his trilogy, Bohr displayed several models of multi-electronic atoms and molecules. To test them with concrete experimental outcomes, he calculated the theoretical values of proper frequencies, using either the ordinary laws of mechanics or quantum postulates for the cases of perturbations perpendicular to the plane of the orbit and electron jumps, respectively. Molecules remained theoretically stable only when their alterations were characterized by these frequencies. Optical dispersion was one of the most effective tools to obtain empirical values of proper frequencies. Since these frequencies did not usually lie in the visible range of the spectrum, they could be derived by fitting the experimental data using eq. (2.2). The hope was that a comparison between theoretical and empirical outcomes could confirm or discard each concrete molecular model.
For example, in the case of
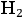 , Bohr put forward a model in which two electrons orbited two nuclei located along the axis of symmetry, see fig. (2.2).
, Bohr put forward a model in which two electrons orbited two nuclei located along the axis of symmetry, see fig. (2.2).
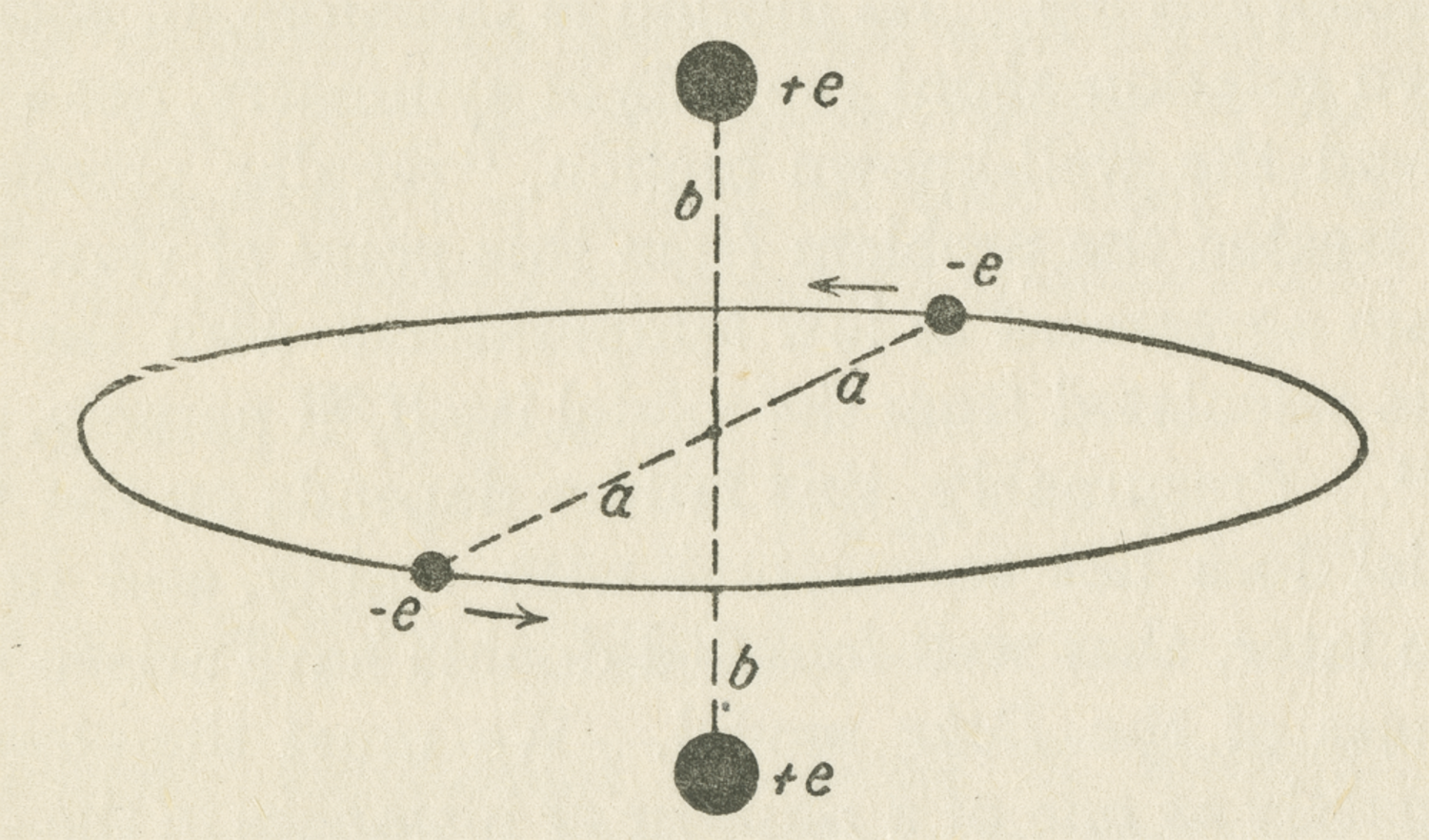
Fig. 2.2: The hydrogen molecule according to Bohr (Reiche 1922, 75).
In this particular instance, the comparison seemingly confirmed Bohr’s model of
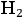 , since the frequency computed from the Cuthbertstons’ experiments on optical dispersion (Cuthbertson and Cuthbertson 1910) turned out to be in agreement with the theoretical values. The results did not provide an unambiguous arbitration concerning the two possible theoretical mechanisms (mechanical or quantum) causing the proper frequency of optical dispersion, for the empirical value was consistent with both. However, since the model of
, since the frequency computed from the Cuthbertstons’ experiments on optical dispersion (Cuthbertson and Cuthbertson 1910) turned out to be in agreement with the theoretical values. The results did not provide an unambiguous arbitration concerning the two possible theoretical mechanisms (mechanical or quantum) causing the proper frequency of optical dispersion, for the empirical value was consistent with both. However, since the model of
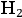 was in any case confirmed, Bohr did not linger over this ambiguity.
was in any case confirmed, Bohr did not linger over this ambiguity.
2.3 Debye and the First Theory of Optical Dispersion According to Bohr’s Model
The first systematic attempt to combine the classical theory of Mitschwingungen with the new picture of matter was carried out by Debye. He chose to address this problem because “a relation between quasi-elastically bounded electrons, which are necessary [in optical dispersion] and the rotating electrons, which are present [in Bohr’s model], is missing” (Debye 1915, 1–2).
Debye took up Bohr’s idea that the atom was like a planetary system, in which the quantum hypothesis came into play by delimiting the angular velocities of electrons. Furthermore, he expanded Bohr’s suggestion that optical dispersion might be caused by mechanical perturbations of stationary orbits. To do so, Debye approached optical dispersion as if it were a purely classical perturbation problem, which he solved for the specific model of
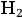 proposed by Bohr.
proposed by Bohr.
More specifically, he assumed that electromagnetic light was able to perturb molecular orbits through Mitschwingungen in the same way as it perturbed proper electron vibrations in Drude’s theory. The essential difference between Debye and Drude was that Debye’s starting point were the concrete equations of motion of the unperturbed orbits, while Drude started from the model of an ordinary oscillator. The quantum of action
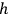 was not brought into play to govern any exchanges of energy between matter and radiation but only entered the calculation of the angular momentum of the stationary orbit.
was not brought into play to govern any exchanges of energy between matter and radiation but only entered the calculation of the angular momentum of the stationary orbit.
Debye’s procedure boiled down to a restoration of the classical connection between the frequencies of matter oscillations (in this case, oscillations of orbits) and the frequency of the emitted light waves. Furthermore, it led to several possible modifications of the orbits instead of the unique modification suggested by Bohr. However, Debye did not dwell on the consequences of his extension of Bohr’s double mechanism. Most importantly, he did not comment on fundamental questions concerning the compatibility between classical and quantum concepts.
Using the experimental data collected by Koch (1913), Debye arrived at a convincing twofold confirmation of his theory. First, the empirical number of dispersion electrons was one and a half times the number predicted by Drude. Debye obtained a new expression for the quantity
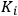 , which filled this gap and restored the agreement with experiments. Second, the proper frequencies
, which filled this gap and restored the agreement with experiments. Second, the proper frequencies
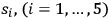 of the five possible perturbations turned out to be proportional to the angular frequency
of the five possible perturbations turned out to be proportional to the angular frequency
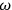 of the orbit via a parameter
of the orbit via a parameter
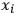 whose value could be calculated theoretically. Using Koch’s data to fix one of the frequencies
whose value could be calculated theoretically. Using Koch’s data to fix one of the frequencies
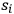 , Debye arrived at a value of
, Debye arrived at a value of
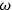 which was in very good agreement with the value calculated using the expression from quantum theory
which was in very good agreement with the value calculated using the expression from quantum theory
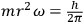 (
(
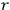 being the radius of the orbit,
being the radius of the orbit,
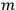 the mass of the electron). Debye considered this a strong confirmation of his theory of optical dispersion from both the standpoint of the adequacy of the procedure and the validity of the specific model of molecular hydrogen.
the mass of the electron). Debye considered this a strong confirmation of his theory of optical dispersion from both the standpoint of the adequacy of the procedure and the validity of the specific model of molecular hydrogen.
A few months later, a doctoral student of Debye’s, Paul Scherrer, extended this procedure to include an explanation of the Faraday effect for a gas of molecular hydrogen.2 Further, Scherrer perceptively spotlighted the question of the compatibility between classical and quantum concepts in Debye’s theory of optical dispersion. For him, its success in explaining experimental data was undoubtedly a “confirmation […] that the classical laws of mechanics can be legitimately applied to the calculation of the perturbations in the inner atom” (Scherrer 1915, 180).
2.4 Sommerfeld and Optical Dispersion in 1915
Sommerfeld also saw a confirmation in the success of Debye’s theory of optical dispersion that the quantum postulates and the classical laws of mechanics and electrodynamics could eventually coexist. Indeed, starting from Debye’s approach, in 1915 Sommerfeld sought to understand the general features of this coexistence: “from [Debye’s theory] one understands that the laws ruling the inner atom do not differ from classical mechanics and electrodynamics as one could presume from Bohr’s postulates” (Sommerfeld 1915, 549).3
From Sommerfeld’s standpoint, Debye’s theory of optical dispersion implicitly suggested the following division between classical and quantum laws: the structure and stationary features of the molecule were determined by quantum laws, while the dynamical process of light dispersion was accounted for by classical physics.
In 1915, Sommerfeld generalized Debye’s approach to optical dispersion to all types of molecules with axial symmetry using a model similar to the one presented in fig. (2.2). As in Debye’s case, Sommerfeld’s treatment relied on the mechanical perturbations induced in the stationary orbits by electromagnetic radiation. The only step of the argument requiring quantum physics was the determination of the angular velocity of the electrons along their orbits in the molecule through the expression
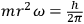 . Quantum jumps were by no means implicated in optical dispersion.
. Quantum jumps were by no means implicated in optical dispersion.
Following this procedure, Sommerfeld eventually arrived at a general expression for the index of refraction as a function of the frequency of light, which could be approximated in the regime of low frequencies by:
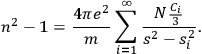
|
2.3 |
This expression showed a close analogy to Drude’s formula (2.2). However, it also entailed a fundamental difference in respect to Drude’s: the singularities of the index of refraction were the proper frequencies
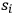 at which the electronic paths were oscillating around their stationary orbits. For Drude,
at which the electronic paths were oscillating around their stationary orbits. For Drude,
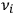 were the proper frequencies of the electrons around their positions of equilibrium.
were the proper frequencies of the electrons around their positions of equilibrium.
Furthermore, the intensity of dispersion
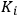 was weighted by a factor
was weighted by a factor
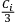 , not present in Drude’s formula, which accounted for the possible anisotropy of the molecule. Indeed, this factor
, not present in Drude’s formula, which accounted for the possible anisotropy of the molecule. Indeed, this factor
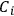 eventually provided a deeper justification to the two-thirds discrepancy between Drude’s expression for the number of dispersion electrons and Koch’s (1913) experimental observations, which had already been accounted for by Debye. Thus, it became clear that Drude’s formulation only held for the isotropic case, when the three proper frequencies of the orbits (radial, azimuthal and axial) were exactly the same.
eventually provided a deeper justification to the two-thirds discrepancy between Drude’s expression for the number of dispersion electrons and Koch’s (1913) experimental observations, which had already been accounted for by Debye. Thus, it became clear that Drude’s formulation only held for the isotropic case, when the three proper frequencies of the orbits (radial, azimuthal and axial) were exactly the same.
Despite the evident advantages of this approach, Sommerfeld openly discussed some conceptual difficulties that plagued the “hybrid” theory, including “a contradiction with electrodynamics […], as the electronic orbits are not allowed to radiate” (Sommerfeld 1915, 549). In effect, the supposition that orbits could radiate energy during optical dispersion contradicted one of Bohr’s postulates: the existence of non-radiating stationary states. Sommerfeld tackled this issue in 1917, in a work I analyze shortly.
In the meantime, the hybrid theory involved inner contradictions that would turn out to be insuperable. Sommerfeld singled out the conflict between quantum and classical physics at exactly the proper frequencies
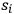 , where the dispersion was discontinuous. Two possible explanations presented themselves. On the one hand,
, where the dispersion was discontinuous. Two possible explanations presented themselves. On the one hand,
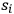 could be considered the proper frequencies at which light was resonantly absorbed. On the other hand, according to Bohr’s theory, those absorption frequencies should coincide with the emission (and thus spectral) frequencies, at which the exchange of electron energy with light was governed by quantum jumps. As it was clear to Sommerfeld that both classical Mitschwingungen and quantum transitions had to be part of the total picture, from his point of view the elaboration of a new theory of optical dispersion meant finding a way for classical and quantum approaches to coexist peacefully and consistently. In this regard, Sommerfeld was trenchant, at the points of discontinuity Bohr won, but in the rest of the spectrum the Mitschwingungen held their validity:
could be considered the proper frequencies at which light was resonantly absorbed. On the other hand, according to Bohr’s theory, those absorption frequencies should coincide with the emission (and thus spectral) frequencies, at which the exchange of electron energy with light was governed by quantum jumps. As it was clear to Sommerfeld that both classical Mitschwingungen and quantum transitions had to be part of the total picture, from his point of view the elaboration of a new theory of optical dispersion meant finding a way for classical and quantum approaches to coexist peacefully and consistently. In this regard, Sommerfeld was trenchant, at the points of discontinuity Bohr won, but in the rest of the spectrum the Mitschwingungen held their validity:
Therefore, our dispersion formula will be correct only at a sufficient distance from the emission and absorption lines and for normal dispersion. How one has to handle anomalous dispersion and the necessary absorption by electrons lies still in the deepest obscurity. (Sommerfeld 1915, 577)
This is how Sommerfeld, by analyzing more deeply the fundamental features of Debye’s theory of optical dispersion, created a divide between the classical and quantum domains.
Nevertheless, the hybrid theory did not work for the specific cases of
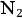 and
and
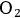 , at least as far as the values of
, at least as far as the values of
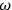 were concerned. Theoretical values were calculated by using the quantum relation
were concerned. Theoretical values were calculated by using the quantum relation
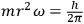 , assuming the axial symmetry of the molecule. For experimental values, Sommerfeld resorted to the already-published experiments on optical dispersion with these gases (Cuthbertson and Cuthbertson 1910). For the case of
, assuming the axial symmetry of the molecule. For experimental values, Sommerfeld resorted to the already-published experiments on optical dispersion with these gases (Cuthbertson and Cuthbertson 1910). For the case of
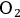 , while experimental data predicted
, while experimental data predicted
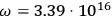 , the theoretical values according to quantum discretization of orbits predicted
, the theoretical values according to quantum discretization of orbits predicted
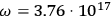 . Sommerfeld was not discouraged. He explained the variance by suggesting that these molecules might not be axially symmetric, and in no way did he suggest that the conceptual grounds of the hybrid theory had been undermined. As this case illustrates, the hybrid theory also entailed a methodological commitment: to find agreement between theory and experiment, physicists should focus on exploring new molecular models.
. Sommerfeld was not discouraged. He explained the variance by suggesting that these molecules might not be axially symmetric, and in no way did he suggest that the conceptual grounds of the hybrid theory had been undermined. As this case illustrates, the hybrid theory also entailed a methodological commitment: to find agreement between theory and experiment, physicists should focus on exploring new molecular models.
2.5 Reactions to Debye-Sommerfeld’s Hybrid Theory
Between 1915 and 1917, articles by several physicists drew attention to the hybrid theory of
 . For instance, within Sommerfeld’s group in Munich, Paul Epstein extended it to the problem of specific heats, and Adalbert Rubinowicz generalized the
Debye-Sommerfeld theory to include the mechanical perturbations in the nuclei of the
. For instance, within Sommerfeld’s group in Munich, Paul Epstein extended it to the problem of specific heats, and Adalbert Rubinowicz generalized the
Debye-Sommerfeld theory to include the mechanical perturbations in the nuclei of the
 molecule. However, not all reactions to the hybrid theory were so positive. The theory also received severe criticism from Hendrika Johanna van Leeuwen, a postdoctoral fellow working under the guidance of Hendrik Antoon Lorentz and Paul Ehrenfest. Her critique concerned the stability of the
molecule. However, not all reactions to the hybrid theory were so positive. The theory also received severe criticism from Hendrika Johanna van Leeuwen, a postdoctoral fellow working under the guidance of Hendrik Antoon Lorentz and Paul Ehrenfest. Her critique concerned the stability of the
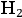 molecule under the influence of external electromagnetic forces. But the strongest arguments against the theory came from Carl Wilhelm Oseen and Bohr. They categorically denied the very possibility that classical and quantum physical laws could truly coexist, which was the essential cornerstone of Sommerfeld’s way of dealing with optical dispersion. The next three sections spell out all these reactions to Debye-Sommerfeld’s hybrid theory.
molecule under the influence of external electromagnetic forces. But the strongest arguments against the theory came from Carl Wilhelm Oseen and Bohr. They categorically denied the very possibility that classical and quantum physical laws could truly coexist, which was the essential cornerstone of Sommerfeld’s way of dealing with optical dispersion. The next three sections spell out all these reactions to Debye-Sommerfeld’s hybrid theory.
2.5.1 Extension to Specific Heats
In 1916, Epstein took up Debye-Sommerfeld’s model of the hydrogen molecule
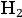 , “which has been strongly supported by Debye’s calculations on dispersion” (Epstein 1916, 400) and extended it to provide a quantum account of rotational specific heats.4
, “which has been strongly supported by Debye’s calculations on dispersion” (Epstein 1916, 400) and extended it to provide a quantum account of rotational specific heats.4
Simultaneously and independently, Frederick Krüger also saw advantages in treating the
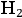 molecule as a gyroscope, see fig. (2.3). Using Felix Klein and Sommerfeld’s theory of the spinning top (Klein and Sommerfeld 1898) he calculated a theoretical value of the precession frequency of Debye-Sommerfeld’s
molecule as a gyroscope, see fig. (2.3). Using Felix Klein and Sommerfeld’s theory of the spinning top (Klein and Sommerfeld 1898) he calculated a theoretical value of the precession frequency of Debye-Sommerfeld’s
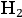 molecule (
molecule (
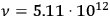 ), which was in satisfactory agreement with the experimental value obtained by Arnold Eucken (1912). Differently from Epstein, however, Krüger did not quantize the motion.
), which was in satisfactory agreement with the experimental value obtained by Arnold Eucken (1912). Differently from Epstein, however, Krüger did not quantize the motion.

Fig. 2.3: The gyroscopic model of a molecular hydrogen (Krüger 1916, 350).
In 1917, Rubinowicz imported the idea of treating Debye-Sommerfeld’s model of
 as a gyroscope back into optics (Rubinowicz 1917). He calculated the proper motions of the molecule, taking into account both oscillations of the electronic orbits and oscillations of the symmetry axis under the influence of very small perturbations. The resulting motions are represented in the pictures below. Further examination led Rubinowicz to realize that indeed none of the precession frequencies he obtained contributed to optical dispersion. However, the oscillation corresponding to case
as a gyroscope back into optics (Rubinowicz 1917). He calculated the proper motions of the molecule, taking into account both oscillations of the electronic orbits and oscillations of the symmetry axis under the influence of very small perturbations. The resulting motions are represented in the pictures below. Further examination led Rubinowicz to realize that indeed none of the precession frequencies he obtained contributed to optical dispersion. However, the oscillation corresponding to case
 , see fig. (2.4), had the same proper frequency as Krüger’s precession frequency in the infrared region of the spectrum. This was very important. Since this approach was a generalization of Debye’s and Sommerfeld’s theory, Rubinowicz’s results provided a bridge between optics and research on specific heats. Optical frequencies were related to the oscillations of orbits, and the frequencies used for specific heats were related to the precession of the symmetry axis. In none of these cases, the exchange of energy took place through quantum transitions, but depended on mechanical motions of molecules, be either vibrations or precessions.
, see fig. (2.4), had the same proper frequency as Krüger’s precession frequency in the infrared region of the spectrum. This was very important. Since this approach was a generalization of Debye’s and Sommerfeld’s theory, Rubinowicz’s results provided a bridge between optics and research on specific heats. Optical frequencies were related to the oscillations of orbits, and the frequencies used for specific heats were related to the precession of the symmetry axis. In none of these cases, the exchange of energy took place through quantum transitions, but depended on mechanical motions of molecules, be either vibrations or precessions.
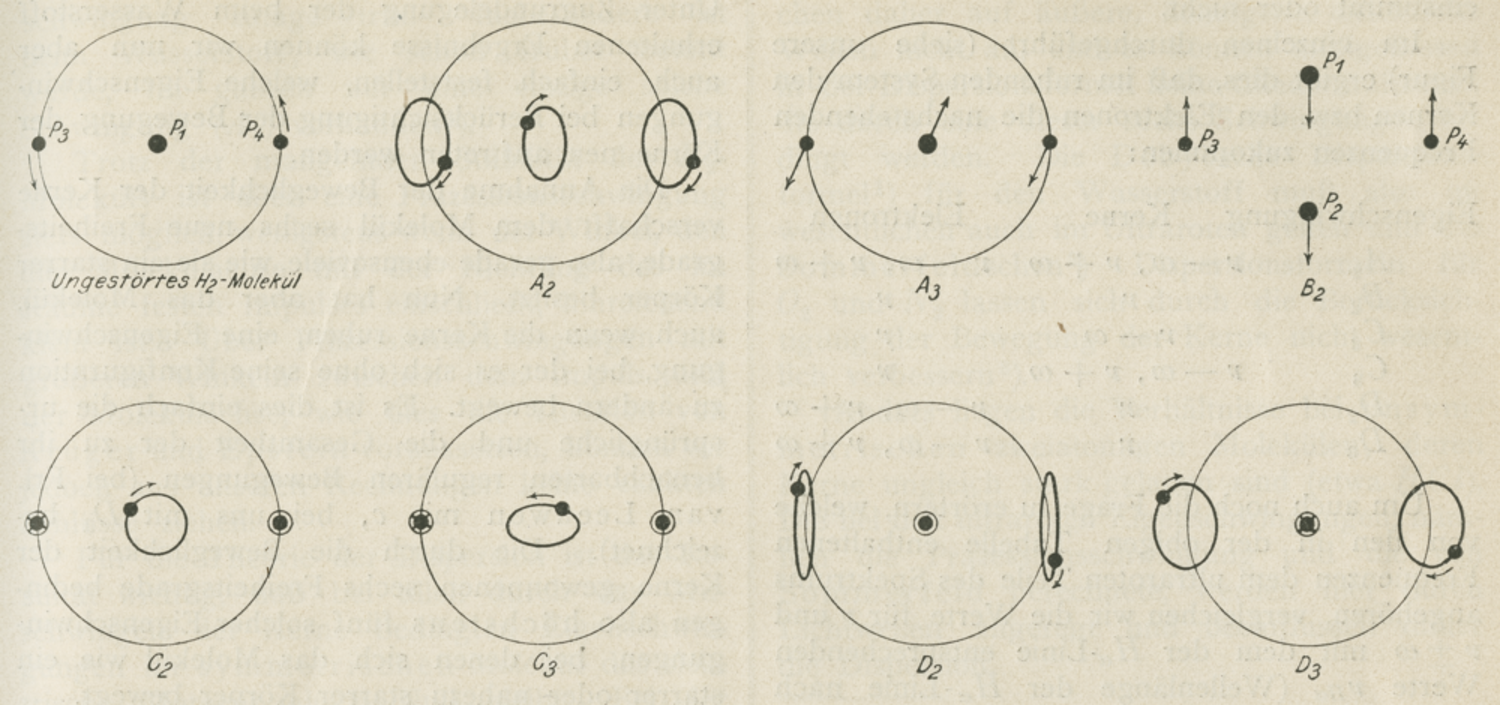
Fig. 2.4: Perturbations of the diatomic molecule according to Rubinowicz (1917, 193).
2.5.2 The Stability Problem
Despite these apparent benefits, the hybrid approach was plagued with difficulties. Ironically, hybridization led to serious problems with stability. The irony lay in that although Bohr’s postulates were meant to overcome the stability problems of early atomic models (and were to some degree successful), the embedding of Mitschwingungen into the new framework, even as small perturbations, brought back the old problems of mechanical instability, as van Leeuwen explained in 1916 (van Leeuwen 1916).
Her detailed analysis of the hybrid theory of
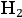 revealed that only three of the six possible proper motions of orbits, see fig. (2.5), had nonzero electric moments and were therefore relevant for dispersion.
revealed that only three of the six possible proper motions of orbits, see fig. (2.5), had nonzero electric moments and were therefore relevant for dispersion.
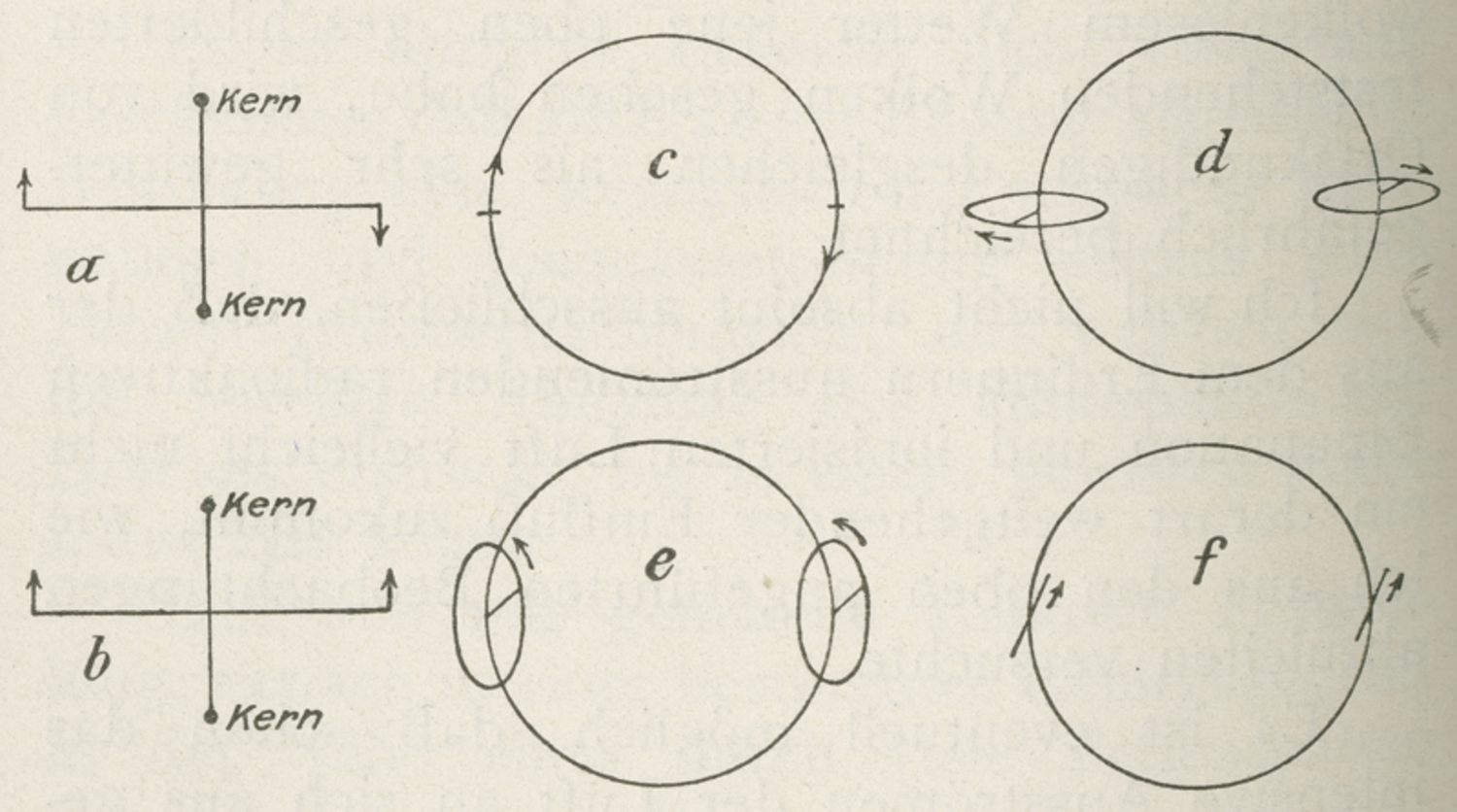
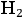 according to van Leeuwen (1916, 196).
according to van Leeuwen (1916, 196).Fig. 2.5: The proper motions of orbits of
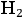 according to van Leeuwen (1916, 196).
according to van Leeuwen (1916, 196).
Furthermore, it turned out that only one of the remaining three could actually contribute to optical dispersion. For only in the case of motion
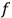 would the orbit keep vibrating after the interruption of the primary radiation and thus be able to emit a secondary radiation. Finally, van Leeuwen determined that the case
would the orbit keep vibrating after the interruption of the primary radiation and thus be able to emit a secondary radiation. Finally, van Leeuwen determined that the case
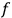 was mechanically unstable, in such a way that the molecule would collapse after interacting with light.
was mechanically unstable, in such a way that the molecule would collapse after interacting with light.
To avoid this dead end, van Leeuwen analytically manipulated Debye-Sommerfeld perturbations, transforming them into mechanically stable oscillations. However, the resulting dispersion formula turned out to be in disagreement with experiments.
Under these circumstances, the only possible solution that van Leeuwen could envision was to overcome the mechanical instability of the molecule by assuming Bohr’s quantum postulates. However, Bohr’s model did not offer the possibility of a consistent treatment of these perturbations of orbits. Thus van Leeuwen concluded that “new assumptions on the equations of motion of [Bohr’s] systems are required and as long as this is not the case, nothing can be said about the corresponding dispersion” (van Leeuwen 1916, 198).
2.5.3 Against the Foundations of the Hybrid Theory
Oseen’s and Bohr’s criticisms went further than van Leeuwen’s. In 1915, Oseen, professor at the University of Uppsala, undertook a general analysis of the compatibility of classical electrodynamics with Bohr’s postulates. He followed a “purely logical” argument, independent of any concrete atomic or molecular model representing the problems of mechanical stability. Oseen concluded that between the quantum theory and the classical electron theory no conciliation was possible. One had to choose between them (Oseen 1915, 405).

Fig. 2.6: Anomalous dispersion in sodium vapor observed using a crossed-prism (Wood 1904, ii).
As mentioned earlier, Bohr had been extremely vague about the connection between the mechanical perturbations of his atomic model and the cause of optical dispersion in 1913, but in 1915 he fully agreed with Oseen. In a letter written 20 December 1915 to Oseen, Bohr expressed his agreement and very effectively summarized the problems of optical dispersion in relation to the available experimental data (italics added by the author):
It seems to me that if the theory of the Hydrogen atom has but the slightest connection with truth, the dispersion (at least in gases) must be a phenomenon of quite a different nature from that assumed by Debye and Sommerfeld. In fact, it appears, e.g., from Wood’s and Bevan’s experiments on the dispersion in sodium and potassium vapors that the characteristic frequencies which determine the dispersion coincide with the frequencies of the principal series in the Sodium and Potassium spectra, and one must therefore expect that the same thing holds for other gases. (Hoyer 1981, 337–338)
Bohr’s mentioning of the experiments of Wood and Bevan deserves some comment. For sodium and potassium vapors, the proper frequencies of optical dispersion were typically located in the visible range of the spectrum. This characteristic made it possible to directly observe the proper frequencies of these substances and compare them with spectral data of these substances. For both substances, it was easy to identify the dispersion frequencies with the spectral frequencies, as shown in this picture obtained by Wood in 1904, see fig. (2.6).
However, Sommerfeld and Debye employed experimental data on molecular gases, specifically
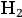 . In this case, no proper frequency was identifiable in the visible spectrum; instead it was located in the ultraviolet. Hence in the hybrid theory, Sommerfeld implicitly assumed that spectral frequencies in the optical range were caused by a quantum process; whereas, the proper frequencies in the ultraviolet stemmed from a classical interaction with light. Bohr, instead, argued that all proper frequencies for the whole spectra had to be caused by the same quantum mechanism, and therefore the program of Debye and Sommerfeld was doomed to fail.
. In this case, no proper frequency was identifiable in the visible spectrum; instead it was located in the ultraviolet. Hence in the hybrid theory, Sommerfeld implicitly assumed that spectral frequencies in the optical range were caused by a quantum process; whereas, the proper frequencies in the ultraviolet stemmed from a classical interaction with light. Bohr, instead, argued that all proper frequencies for the whole spectra had to be caused by the same quantum mechanism, and therefore the program of Debye and Sommerfeld was doomed to fail.
Oseen was pleased to learn that Bohr shared his opinion. Indeed, he replied to Bohr on 3 March 1916 adding a somewhat more personal evaluation of the reactions of Debye and Sommerfeld to his criticisms:
The two gentlemen have received my criticism in quite different ways. Debye admitted without reservation that there were internal contradictions in the theory but explained that he saw his mission in groping his way with attempts at hypotheses. Sommerfeld however would maintain that the theory does possess inner consistency. The hydrogen molecules should emit energy during the oscillations of the electron around the radiationless orbit, and the dispersion should originate in this emission. (Hoyer 1981, 570)
Debye seemed to have developed his theory without paying much attention to the compatibility between classical and quantum approaches; thus, he did not defend it when problems emerged. Reacting very differently, Sommerfeld took this question much more seriously in 1915, and he reiterated to Oseen his firm conviction concerning the classical aspects of the problem.
On 19 March, Bohr took up his pen and wrote to Sommerfeld. His letter in no way concealed his critical reservations regarding his German colleague’s treatment of dispersion theory:
It appears to me, however, that the experiments on the dispersion in sodium and potassium vapors of Wood and Bevan indicate that the dispersion cannot be determined by means of ordinary mechanics and electrodynamics from the constitution of the systems in the stationary states, but must depend essentially on the same mechanism as the transitions between the different states. (Hoyer 1981, 604)
Sommerfeld appreciated Bohr’s criticisms but he insisted, in a reply from 20 August 1916, that the structure of the molecule was fixed by quantum postulates, while optical dispersion in molecules was purely classical. On that matter, he had “full scores of still unpublished calculations and results” (Eckert and Märker 2000, 565).
2.6 Sommerfeld’s Counterattack
In 1917, Sommerfeld published another paper on optical dispersion, including the “unpublished calculations” that he mentioned to Bohr in the letter from the preceding August in 1916. In this paper, Sommerfeld deepened the divide between classical physics and quantum theory that he put forward in 1915 and subsequently refuted Oseen’s and Bohr’s claims (Sommerfeld 1917). For these purposes, Sommerfeld introduced a new ingredient into his discussion of dispersion: Ehrenfest’s adiabatic principle.
The adiabatic principle allowed Sommerfeld to avoid the previously discussed conceptual contradictions between the treatment of discrete spectra and the treatment of optical dispersion. He achieved this in the following manner: an orbit was perturbed by incoming light, but as long as the ratio between its frequency and the orbital velocity of electrons was infinitesimal, all new perturbed states resulting from the initial stationary states could also be considered stationary states, on account of the adiabatic principle. Thus the continuous transition from one adiabatically modified state to another could cause continuous emission of secondary radiation without contradicting the quantum postulates.5
Sommerfeld also employed the adiabatic principle to address another important disparity. Quantum transitions involved in the production of spectral lines occurred only in atoms, while the adiabatic perturbation of orbits from which dispersion originated only occurred in molecules. “Is there any contradiction in this different treatment of atom and molecule?” Sommerfeld asked himself in the paper. Enthusiastically he answered: “we claim: Nein!” (Sommerfeld 1917, 502).
Thus, Sommerfeld’s strategy was twofold. First, he used the adiabatic principle to bridge the gaps between quantum emission and classical emission processes involving perturbed stationary states. This in turn established a new division between atomic and molecular processes, which allowed Sommerfeld to deprive Bohr’s criticism of its experimental support. Wood’s and Bevan’s results on sodium and potassium vapors turned out to be irrelevant to the discussion of the hybrid theory.6
As in 1915, Sommerfeld looked for consistency between his theory and the available experimental data on
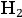 ,
,
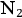 and
and
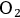 . As I discussed in sec. (2.4), experiments implied an angular frequency
. As I discussed in sec. (2.4), experiments implied an angular frequency
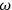 that was at odds with the value calculated from the quantum expression
that was at odds with the value calculated from the quantum expression
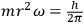 . In 1915, Sommerfeld had tried to explain the discrepancy by appealing to possible asymmetrical configurations of the molecules. In 1917, he went so far as to invent a new quantum rule. He replaced the usual formula with
. In 1915, Sommerfeld had tried to explain the discrepancy by appealing to possible asymmetrical configurations of the molecules. In 1917, he went so far as to invent a new quantum rule. He replaced the usual formula with
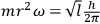 (
(
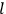 being the valence number). Admittedly, Sommerfeld could not present any “theoretical foundation for this general quantum assumption” (Sommerfeld 1917, 547), although it allowed him to maintain the validity of mechanics and electrodynamics in the inner molecule.7
being the valence number). Admittedly, Sommerfeld could not present any “theoretical foundation for this general quantum assumption” (Sommerfeld 1917, 547), although it allowed him to maintain the validity of mechanics and electrodynamics in the inner molecule.7
Finally, Sommerfeld evaded the problems of stability of the
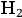 molecule raised in 1915 and 1916 by van Leeuwen and Rubinowicz by alluding to the possibility of a still-unknown quantum constraint:
molecule raised in 1915 and 1916 by van Leeuwen and Rubinowicz by alluding to the possibility of a still-unknown quantum constraint:
[F]rom the point of view of the usual mechanics, the models are unstable in a peculiar way. […] One has to conceive a special quantum constraint on the motions in order to avoid the unstable collapse of the model. (Sommerfeld 1917, 547)
In the ensuing years, the discussion on the hybrid theory of optical dispersion reached a point of stagnation. However, Sommerfeld’s division between atomic and molecular processes made an impact. In his early monograph on quantum theory, Fritz Reiche presented optical dispersion in a separate chapter devoted to “phenomena of molecular models,” thus endorsing Sommerfeld’s viewpoint (Reiche 1922, 117–124).
2.7 From the Hybrid Theory to the Light Quantum
Although no alternative theory of optical dispersion threatened to overshadow the hybrid theory, from 1917 to the early 1920s, Sommerfeld’s position changed significantly.
In a letter sent to Bohr on 5 February 1919, Sommerfeld inquired about his viewpoint on the theory of optical dispersion. On this occasion, Sommerfeld did not defend his earlier theory at all costs as he had done in the 1917 paper. He even challenged Bohr to seek a better solution:
I am very excited about your position on dispersion theory. I would be very happy if you found a better approach to it. If you could replace themodel, which is full of contradictions, with something better, I don’t have any objection. (Eckert and Märker 2004, 48)
Some months later, in a letter dated 19 November 1919 to Sommerfeld, Bohr attached a copy of his 1916 unpublished paper in which he unveiled the details of his argument against the hybrid theory.8
Once again, Bohr resorted to Wood’s and Bevan’s experiments to reiterate his point about the absence of a disparity between the quantum and classical domains of knowledge. After all, Bohr argued, Debye’s successful account of dispersion in hydrogen was due to a close coincidence, in this particular case, between the characteristic frequencies of the orbits according to ordinary electrodynamics and those determined by the quantum relations.
Moreover, Bohr highlighted another difficulty of the hybrid theory: Wood’s and Bevan’s experiments revealed that the intensity of optical dispersion changed depending on the proper frequency considered. This behavior could not be explained by Sommerfeld’s assumed proportionality between the intensity of optical dispersion and the number
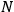 of the valence electrons, weighted by a factor
of the valence electrons, weighted by a factor
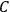 related to the anisotropy of the molecule. Bohr put forward an alternative explanation: the different values of
related to the anisotropy of the molecule. Bohr put forward an alternative explanation: the different values of
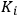 relating to different frequencies were somehow connected with the greater tendency of the quantum jumps to occur between successive stationary states than between more distant states.
relating to different frequencies were somehow connected with the greater tendency of the quantum jumps to occur between successive stationary states than between more distant states.
This connection between dispersion and transition also worked in the opposite direction, suggesting a very interesting analogy to Bohr: the mechanism of transition between different stationary states resembled the mechanism of interaction of light with a classical electrodynamic vibrator: “[i]f the above view is correct […] we must, on the other hand, assume that this mechanism [of transitions] shows a close analogy to an ordinary electrodynamic vibrator” (Hoyer 1981, 449).
Months later Sommerfeld voiced a very skeptical opinion about the hybrid theory of optical dispersion:
Debye’s apparent success with hydrogen calls us to a challenge. In the meantime, we have realized that this problem is not ripe yet, even if we exclude the case of the resonance between the exciting optical field and the proper frequencies of the atom, as I did in the past. (Sommerfeld 1921, 500)
To support this statement, Sommerfeld made use of Bohr’s own argument: he highlighted the identicality between the absorption lines of optical dispersion and the spectral lines in sodium and potassium gases. Eventually, Sommerfeld accepted the quantum nature of optical dispersion.
This new attitude did not imply Sommerfeld’s subscription to Bohr’s program of bridging quantum and classical physics through the correspondence principle. Sommerfeld never concealed his skepticism about the correspondence principle. In a letter dated 11 November 1920, Sommerfeld added a comment on his treatment of the correspondence principle in the second edition of Atombau und Spektrallinien:
In the addenda of my book, you can see that I took the pain to formulate your correspondence principle better than I did in the first edition. […] However I have to admit that the quantum theoretical root of your principle seems to me still awkward, although I also have to acknowledge that in this way an important relation between the quantum theory and the classical electrodynamics is revealed. (Eckert and Märker 2004, 86–87)
An alternative to the “awkward” correspondence principle was developed some years later by Gregor Wentzel and Karl Herzfeld, two of Sommerfeld’s collaborators in Munich. They relinquished the correspondence principle and the wave picture, relying instead on a purely quantum theory of light. To be sure, Sommerfeld had been advocating the quantum theory of light since 1923, shortly after he heard about Arthur Compton’s experiments. Upon his return from a lecture trip in the United States, on 27 November 1923, Sommerfeld expressed to Max von Laue his conviction that the new theory of light could pave the way for a refutation of the correspondence principle:
Now I really have a stronger and stronger feeling that the wave theory (and the field theory) must be dismissed. Therefore Bohr’s correspondence principle seems to me more and more unsatisfactory however indispensable it is. (Eckert and Märker 2004, 156)
In the same vein as these comments, Sommerfeld reiterated his doubts about the correspondence principle on the occasion of the fourth edition of Atombau und Spektrallinien: “personally we would like to preserve a greater hope in the magic of the quantum, rather than in considerations on correspondence or stability” (Sommerfeld 1924, 192).
These ideas also entered the daily scientific life of Sommerfeld’s Theoretical Physics Institute at the University of Munich. As early as 16 November 1923, in the regularly-scheduled Wednesday colloquium, the discussion hinged on a report about “Light Quantum Hypothesis and Lattice Interference,” presented by Gregor Wentzel.9 Indeed, Wentzel published a paper on a similar topic shortly thereafter (Wentzel 1924). In the same year, Herzfeld took up Wentzel’s ideas and applied them to optical dispersion. Both optical dispersion and the interference of light had been hitherto the most serious difficulties for the theory of light quanta.
The first step in overcoming these difficulties was to define a phase for light quanta. Wentzel (1924) had postulated that the phase of a light quantum corresponded to the
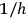 part of its action integral along a path
part of its action integral along a path
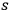 between two stationary states of Bohr’s atom. The phase determined a wave of probability for this light quantum to follow the path
between two stationary states of Bohr’s atom. The phase determined a wave of probability for this light quantum to follow the path
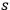 .
.
Relying on the idea of the quantum phase, Herzfeld developed a theory of optical dispersion in terms of light quanta (Herzfeld 1924). He also postulated the existence of certain stationary Zwischenbahnen (intermediate orbits) between Bohrian stationary states. If the frequency defined by the energy difference between the states was
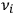 , a light quantum of corresponding frequency was immediately absorbed by the atom or molecule. By contrast, if the frequency
, a light quantum of corresponding frequency was immediately absorbed by the atom or molecule. By contrast, if the frequency
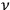 of the incoming light quantum did not coincide with
of the incoming light quantum did not coincide with
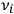 , then the light quantum stayed for a duration of
, then the light quantum stayed for a duration of
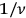 on the Zwischenbahnen before being reemitted. Drawing on formal similarities with the classical Mitschwingungen, Herzfeld stated that the delay of
on the Zwischenbahnen before being reemitted. Drawing on formal similarities with the classical Mitschwingungen, Herzfeld stated that the delay of
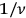 caused a phase delay, according to Wentzel’s definition of quantum phase.
caused a phase delay, according to Wentzel’s definition of quantum phase.
Thus, with the work of Herzfeld and Wentzel, all vestiges of the old classical mechanism disappeared. Herzfeld’s approach led to a physical system in which the only mechanism of energy exchange between light and matter boiled down to transitions between states. The intensity as well as the time-dependency of optical dispersion were due to the dependence of the probability of light quanta being absorbed and reemitted on the ratio between their frequency and the frequency of transition.
2.8 A New Thread of the Story
Parallel to these theoretical developments, the quantum aspects of optical dispersion emerged from a very different perspective. Novel insights arose from experimental research by Otto Stern and Max Volmer (1919). They were dealing with another crucial optical phenomenon: fluorescence.
This phenomenon occurred when certain substances transformed the radiative energy they absorbed into secondary light, normally of lower frequency than the original radiation. In particular, Stern and Volmer were concerned with the exponential decrease of intensity of fluorescence, being parametrized with respect to the decay time
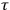 . Classically, one expected that
. Classically, one expected that
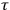 was of the same order of magnitude as the mean time between two molecular collisions. However, in a series of experiments using gaseous iodine, Stern and Volmer concluded that the decay time was indeed much shorter than expected, and it was independent of the pressure of the gas, thus the frequency of collisions.
was of the same order of magnitude as the mean time between two molecular collisions. However, in a series of experiments using gaseous iodine, Stern and Volmer concluded that the decay time was indeed much shorter than expected, and it was independent of the pressure of the gas, thus the frequency of collisions.
As an alternative, Stern and Volmer attempted a quantum explanation of the fluorescence process. But, how can a time-dependent process as the exponential decrease of intensity be explained using quantum jumps? Stern and Volmer reinterpreted the decay time
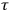 as the mean lifetime of the molecules in one state
as the mean lifetime of the molecules in one state
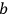 . In doing so, they used the analogy Einstein had established in 1916–1917 between the process of spontaneous emission through quantum transitions and the decay of radioactivity governed by a statistical law (Einstein 1917). This decision implied that the only mechanism of light-matter interaction occurring in fluorescence was a quantum mechanism, namely, quantum transitions.
. In doing so, they used the analogy Einstein had established in 1916–1917 between the process of spontaneous emission through quantum transitions and the decay of radioactivity governed by a statistical law (Einstein 1917). This decision implied that the only mechanism of light-matter interaction occurring in fluorescence was a quantum mechanism, namely, quantum transitions.
Eventually, to give a time-dependent explanation of the whole process, Stern and Volmer proposed the equivalence of one quantum of energy
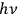 with one monochromatic classical resonator of the same frequency. And they made use of the analogy in the following way: if the macroscopic decay time of a gas of
with one monochromatic classical resonator of the same frequency. And they made use of the analogy in the following way: if the macroscopic decay time of a gas of
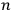 molecules could be identified with
molecules could be identified with
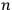 molecular classical resonators having the same decay time, according to quantum physics, the decay time is related to the decrease in number of resonators that jump from state
molecular classical resonators having the same decay time, according to quantum physics, the decay time is related to the decrease in number of resonators that jump from state
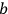 to state
to state
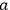 at each moment,
at each moment,
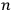 being the initial number of resonators at the state
being the initial number of resonators at the state
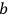 . Thus, by applying the analogy to the classical resonator, the time-dependent molecular process could be translated into a question of the probabilities of quantum transitions.
. Thus, by applying the analogy to the classical resonator, the time-dependent molecular process could be translated into a question of the probabilities of quantum transitions.
From this, one could draw further consequences for other phenomena, most importantly for optical dispersion. Stern and Volmer suggested that, with their analogy between a quantum of energy
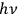 and a classical resonator of frequency
and a classical resonator of frequency
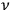 in hand, Drude’s classical mechanism could easily be translated into a process involving only quantum transitions and rates of transitions. Thus, all proper frequencies of optical dispersion would coincide with transition frequencies, as the experiments appeared to require.
in hand, Drude’s classical mechanism could easily be translated into a process involving only quantum transitions and rates of transitions. Thus, all proper frequencies of optical dispersion would coincide with transition frequencies, as the experiments appeared to require.
Two years later, experimentalist Rudolf Ladenburg, aware of Stern and Volmer’s results, explained the experimental data on the number of “dispersion electrons” by using a similar analogy and also resorting to a probabilistic description of the elementary processes (Ladenburg 1921). Ladenburg identified the mean energy of
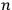 classical damped oscillators with the energy emitted by
classical damped oscillators with the energy emitted by
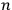 molecules through quantum transitions. The latter value depended on the number
molecules through quantum transitions. The latter value depended on the number
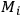 of molecules on the state
of molecules on the state
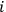 , statistical weights
, statistical weights
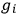 and
and
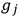 of states
of states
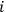 and
and
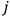 , the probability coefficient
, the probability coefficient
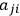 for spontaneous transition between these states, and the frequency of light absorbed in the jump
for spontaneous transition between these states, and the frequency of light absorbed in the jump
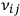 . On these grounds, Ladenburg redefined the number
. On these grounds, Ladenburg redefined the number
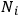 of dispersion electrons appearing in the intensity
of dispersion electrons appearing in the intensity
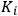 discussed in sec. (2.1.2) as:
discussed in sec. (2.1.2) as:
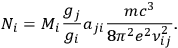
|
2.4 |
Note that now the intensity was neither dependent on the anisotropy of the molecule, as Sommerfeld had suggested, nor proportional to the number of electrons, as Drude had assumed. Rather, the intensity depended on the probability of transition between two quantum states.
In 1923, Ladenburg and Reiche further developed the analogy with a classical resonator and formalized a kind of fictive oscillator, which they called an Ersatzoszillator (Ladenburg and Reiche 1923). These oscillators played the same role in the exchange of energy between light and matter as the resonating electrons in classical accounts. With this move, Ladenburg and Reiche achieved two results. First, the time-dependent features of optical dispersion—the delayed reemission of secondary radiation by matter—were explained according to the classical model of Mitschwingungen. Second, resonance occurred necessarily at spectral frequencies and not at mechanical frequencies, as in the Debye-Sommerfeld theory.
It has been well documented in the secondary literature that the introduction of these Ersatzoszillatoren eventually led to the “virtual oscillators” of the Bohr-Kramers-Slater (BKS) theory elaborated by Bohr and two collaborators, Hendrik Kramers and John Slater, in 1924. Although the BKS theory was soon disproved by experiments, some of its essential features remained in later accounts. Also in 1924, Kramers no longer pictured literal virtual oscillators, but resorted to the correspondence principle when elaborating the first full quantum theory of optical dispersion, based on the formal analogy between a quantum system and a system of classical oscillators perturbed by electromagnetic light (Kramers 1924).10
2.9 Conclusion
The preceding analysis has shown how optical dispersion constituted an ideal arena for discussing whether there was a divide between classical and quantum physics, which physical features had to be considered characteristically classical or quantum, and how this division influenced the creation of a consistent theoretical account.
From 1913 to 1924, the transformation of optical dispersion passed through two distinct phases. In the first phase, in the aftermath of Bohr’s atomic model, it aroused a dispute between Sommerfeld and Bohr on the ultimate nature of the phenomenon, whether it was essentially classical or quantum.
In the second phase, from 1920 onward, dispersion was recognized as a quantum phenomenon, and different strategies emerged to deal with it. The two phases of the story were actually methodologically related. The way in which Bohr and Sommerfeld defined the divide between classical and quantum before 1920 had a bearing on the different strategies they chose to deal with dispersion as a quantum process after 1920.
From 1915 to 1919, Sommerfeld set the divide between the classical and quantum domains on the basis of Debye’s hybrid theory. On one side lay spectroscopy and atoms, on the other, optical dispersion and molecules. Thus Sommerfeld’s strategy was rooted in negotiating the divide between classical and quantum through the classification of phenomena according to the nature of their physical mechanisms.
Bohr’s strategy was very different. He did not recognize any disparity between optical dispersion and spectroscopy or, more generally, between classical and quantum laws. Bohr considered optical dispersion a quantum phenomenon. In 1916, he hinted at the analogy between a classical oscillator and a quantum transition, and this analogy allegedly led to combining the continuous features of Mitschwingungen with quantum jumps.
After 1920, Sommerfeld and Bohr agreed on the quantum nature of optical dispersion. However, their approaches remained divergent. In Sommerfeld’s school, the search for a physical mechanism remained very popular. Indeed, Herzfeld and Wentzel did not confine themselves to the formal analogy between the phase delay of the Mitschwingungen and the sojourn time of the light quantum in an atom, but they looked for a completely new mechanism of optical dispersion based on the concept of light quanta.11 In contrast, in 1924, Kramers developed the first quantum theory of optical dispersion using Bohr’s correspondence principle and a formal analogy between the quantum system and a system of classical electrodynamic oscillators perturbed by electromagnetic light, without providing any new explicit mechanism of interaction between light and matter.
Abbreviations and Archives
| AHQP | Archive for History of Quantum Physics. American Philosophical Society, Philadelphia |
Acknowledgements
This paper has been written in the framework of the project “History and Foundations of Quantum Physics” of the Max Planck Institute for the History of Science (MPIWG) and the Fritz Haber Institute of the Max Planck Society. It is also part of my ongoing PhD project, which I am carrying out under the joint supervision of Jürgen Renn (MPIWG) and Luis Navarro (University of Barcelona). My research has been financially supported with the pre-doctoral fellowships of the Generalitat of Catalunya and the Max Planck Society. I also would like to thank the editors of this volume, Shaul Katzir, Christoph Lehner, and Jürgen Renn, Alexei Kojevnikov, and my colleagues of the “History and Foundations of Quantum Physics Project” for their constructive comments on my paper’s drafts. I am very much indebted to Jeremiah James for his linguistic advice. Finally, I would also like to express my gratitude to Michel Janssen for having introduced me to the fascinating research subject of optical dispersion, and very specifically to Massimiliano Badino for the innumerable discussions, and above all, for his unconditional support.
References
Abegg, Richard (1904). Die Valenz und das periodische System. Versuch einer Theorie der Molekularverbindungen. Zeitschrift für anorganische Chemie 39: 330-380
Bevan, P. V. (1910). Dispersion of Light by Potassium Vapour. Proceedings of the Royal Society A 84: 209-225
Bohr, Niels (1913a). On the Constitution of Atoms and Molecules. Part I. Philosophical Magazine 26: 1-25
- (1913b). On the Constitution of Atoms and Molecules. Part II. Philosophical Magazine 26: 476-502
- (1913c). On the Constitution of Atoms and Molecules. Part III. Philosophical Magazine 26: 857-875
Buchwald, Jed (1985). From Maxwell to Microphysics. Chicago: The University of Chicago Press.
Christiansen, Christian (1870). Über die Brechungsverhältnisse einer weingeistigen Lösung des Fuchsins. Annalen der Physik 217: 479-480
Cuthbertson, Clive, Maude Cuthbertson (1910). On the Refraction and Dispersion of Air, Oxygen, Nitrogen, and Hydrogen, and Their Relations. Proceedings of the Royal Society A 83: 151-171
Debye, Peter (1915). Die Konstitution des Wasserstoff-Moleküls. Sitzungsberichte der Bayerischen Akademie zu München
Drude, Paul (1894). Physik des Aethers auf elektromagnetischer Grundlage. Stuttgart: Ferdinand Enke.
- (1900). Lehrbuch der Optik. Stuttgart: Hirzel.
- (1904a). Optische Eigenschaften und Elektronentheorie. I. Teil. Annalen der Physik 319(9): 677-725
- (1904b). Optische Eigenschaften und Elektronentheorie. II. Teil. Annalen der Physik 319(10): 936-961
Duncan, Anthony, Michel Janssen (2007). On the Verge of . Archive for History of Exact Sciences 61: 553-671
Eckert, Michael (1993). Die Atomphysiker. Eine Geschichte der theoretischen Physik am Beispiel der Sommerfeldschule. Braunschweig: Vieweg.
Eckert, Michael, Karl Märker (2000). Arnold Sommerfeld: Wissenschaftlicher Briefwechsel, Band 1: 1892–1918. Berlin: Verlag für die Geschichte der Naturwissenschaften und der Technik.
- (2004). Arnold Sommerfeld: Wissenschaftlicher Briefwechsel, Band 2: 1919–1951. Berlin: Verlag für die Geschichte der Naturwissenschaften und der Technik.
Ehrenfest, Paul (1913). Bemerkung betreffs der spezifischen Wärme zweiatomiger Gase. Verhandlungen der Deutschen Physikalischen Gesellschaft 15: 451-457
Einstein, Albert (1917). Zur Quantentheorie der Strahlung. Physikalische Zeitschrift 18: 121-128
Einstein, Albert, Otto Stern (1913). Einige Argumente für die Annahme einer molekularen Agitation beim absoluten Nullpunkt. Annalen der Physik 345: 551-560
Epstein, Paul S. (1916). Über die spezifische Wärme des Wasserstoffs. Verhandlungen der Deutschen Physikalischen Gesellschaft 18: 398-413
Eucken, Arnold (1912). Die Molekularwärme des Wasserstoffs bei tiefen Temperaturen. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin
Franck, James, Robert Wood (1911). Über die Überführung des Resonanzspektrums der Jodfluoreszenz in ein Bandspektrum durch Zumischung mit Helium. Physikalische Zeitschrift 12: 81-83
Gearhart, Clayton A. (2010). `Astonishing Successes' and `Bitter Disappointment': The Specific Heat of Hydrogen in Quantum Theory. Archive for History of Exact Sciences 64: 113-202
Glazebrook, Richard (1886). Report on Optical Theories. In: British Association for the Advancement of Science. Report–1885 London: Spottiswoode 157-261
von Helmholtz, Hermann (1875). Zur Theorie der anomalen Dispersion. Annalen der Physik 230: 582-596
- (1892). Elektromagnetische Theorie der Farbenzerstreuung. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin
Herzfeld, Karl (1924). Versuch einer quantenhaften Deutung der Dispersion. Zeitschrift für Physik 23: 341-360
Hoyer, Ulrich (1981). Niels Bohr Collected Works. Volume 2. Work on Atomic Physics (1912–1917). Amsterdam: North-Holland Publishing Company.
Kauffmann, Hugo (1902). Die Valenzlehre. Ein Lehr- und Handbuch für Chemiker und Physiker. Stuttgart: Ferdinand Enke.
Kaufmann, Walter (1902). Die elektromagnetische Masse des Elektrons. Physikalische Zeitschrift 4: 54-57
- (1906). Über die Konstitution des Elektrons. Annalen der Physik 324: 487-553
Klein, Felix, Arnold Sommerfeld (1898). Über die Theorie des Kreisels. Stuttgart: B. G. Teubner.
Koch, John (1913). Über die Dispersion gasförmiger Körper im ultravioletten Spektrum. Arkiv för Matematik, Astronomi och Fysik 8: 1-25
Kramers, Hendrik A. (1924). The Quantum Theory of Dispersion. Nature 114: 310-311
Krüger, Friederick (1916). Über die Eigenschwingungen freier Kreiselmoleküle. Annalen der Physik 355: 346-368
Kundt, August (1870). Über die anomale Dispersion der Körper mit Oberflächenfarben. Annalen der Physik 218: 346-368
- (1871a). Über anomale Dispersion. Annalen der Physik 219: 259-269
- (1871b). Über anomale Dispersion, Dritte Mittheilung. Annalen der Physik 220: 128-137
- (1872). Über anomale Dispersion, Vierte Mittheilung. Annalen der Physik 221: 67-80
Ladenburg, Rudolf (1921). Die quantentheoretische Deutung der Zahl der Dispersionselektronen. Zeitschrift für Physik 4: 451-468
Ladenburg, Rudolf, Stanisław Loria (1908). Über die Dispersion des leuchtenden Wasserstoffs. Physikalische Zeitschrift 9: 875-878
Ladenburg, Rudolf, Fritz Reiche (1923). Absorption, Zerstreuung und Dispersion in der Bohrschen Atomtheorie. Die Naturwissenschaften 11: 584-598
Laski, Gerda (1919). Ultrarote Eigenfrequenzen zweiatomiger Bohrscher Gasmoleküle und die spezifische Wärme bei hohen Temperaturen. Physikalische Zeitschrift 20: 269-274
Laue, Max (1905). Die Fortpflanzung der Strahlung in dispergierenden und absorbierenden Medien. Annalen der Physik 323: 523-566
van Leeuwen, Hendrika Johanna (1916). Die Instabilität des Bohr-Debyeschen Wasserstoff-Moleküls und die Dispersion von Wasserstoff. Physikalische Zeitschrift 17: 196-198
Loria, Stanisław (1914). Die Lichtbrechung in Gasen als physikalisches und chemisches Problem. Braunschweig: Friedrich Vieweg und Sohn.
Navarro, Luis, Enric Pérez (2006). Paul Ehrenfest: the Genesis of the Adiabatic Hypothesis, 1911–1914. Archive for History of Exact Sciences 60: 209-267
Oseen, Carl Wilhelm (1915). Das Bohrsche Atommodell und die Maxwellschen Gleichungen. Physikalische Zeitschrift 16: 395-405
Pérez, Enric (2009). Ehrenfest's Adiabatic Hypothesis and the Old Quantum Theory, 1916–1918. Archive for History of Exact Sciences 63: 81-127
Reiche, Fritz (1922). The Quantum Theory. London: MeuthenCo..
Rubinowicz, Adalbert (1917). Die Eigenschwingungen des Bohr-Debyeschen Wasserstoffmoleküls bei Berücksichtigung der Bewegung der Kerne. Physikalische Zeitschrift 18: 187-195
Scherrer, Paul (1915). Die Rotationsdispersion des Wasserstoffs. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen 1: 179-185
Schwarzschild, Karl (1916). Zur Quantenhypothese. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin
Sellmeier, Wolfgang (1872a). Über die durch die Aetherschwingungen erregten Mitschwingungen der Körpertheilchen und deren Rückwirkung auf die ersteren, besonders zur Erklärung der Dispersion und ihrer Anomalien. Annalen der Physik 219: 399-421
- (1872b). Über die durch die Aetherschwingungen erregten Mitschwingungen der Körpertheilchen und deren Rückwirkung auf die ersteren, besonders zur Erklärung der Dispersion und ihrer Anomalien. Annalen der Physik 219: 520-549
- (1872c). Über die durch die Aetherschwingungen erregten Mitschwingungen der Körpertheilchen und deren Rückwirkung auf die ersteren, besonders zur Erklärung der Dispersion und ihrer Anomalien. Annalen der Physik 221: 386-408
- (1872d). Über die durch die Aetherschwingungen erregten Mitschwingungen der Körpertheilchen und deren Rückwirkung auf die ersteren, besonders zur Erklärung der Dispersion und ihrer Anomalien. Annalen der Physik 221: 525-544
Seth, Suman (2010). Crafting the Quantum: Arnold Sommerfeld and the Practice of Theory, 1890–1926. Boston: MIT Press.
Sommerfeld, Arnold (1907). Ein Einwand gegen die Relativtheorie der Elektrodynamik und seine Beseitigung. An der Diskussion beteiligten sich W. Wien, Braun, Voigt, Des Coudres. Physikalische Zeitschrift 8: 841-842
- (1912). Über die Fortpflanzung des Lichtes in dispergierenden Medien. In: Festschrift Heinrich Weber zu seinem siebzigsten Geburtstag am 5. März 1912 Leipzig: B. G. Teubner 338-374
- (1915). Die allgemeine Dispersionsformel nach dem Bohrschen Modell. In: Arbeiten aus den Gebieten der Physik, Mathematik, Chemie: Festschrift Julius Elster und Hans Geitel zum sechzigsten Geburtstag Ed. by Karl Bergwitz. Braunschweig: Vieweg und Sohn 549-584
- (1916). Zur Quantentheorie der Spektrallinien. Annalen der Physik 356: 1-94
- (1917). Die Drudesche Dispersionstheorie vom Standpunkte des Bohrschen Modelles und die Konstitution von . Annalen der Physik 358: 497-550
- (1921). Zur Kritik der Bohrschen Theorie der Lichtemission. Jahrbuch der Radioaktivität und Elektronik 17: 417-429
- (1924). Atombau und Spektrallinien. Braunschweig: Vieweg.
Stark, Johannes (1916). Beobachtungen über den zeitlichen Verlauf der Lichtemissionen in Spektralserien. Annalen der Physik 354: 731-768
Stern, Otto, Max Volmer (1919). Über die Abklingungszeit der Fluoreszenz. Physikalische Zeitschrift 20: 183-188
Voigt, Woldemar (1899). Über die Änderung der Schwingungsform des Lichtes beim Fortschreiten in einem dispergierenden oder absorbierenden Mittel. Annalen der Physik 304: 598-603
- (1901). Weiteres zur Änderung der Schwingungsform des Lichtes beim Fortschreiten in einem dispergierenden und absorbierenden Mittel. Annalen der Physik 309: 209-214
Wentzel, Gregor (1924). Zur Quantenoptik. Zeitschrift für Physik 22: 193-199
Whittaker, Edmund (1910). A History of the Theories of Aether and Electricity: From the Age of Descartes to the Close of the Nineteenth Century. London: Longman, GreenCo.
Wood, Robert (1904). A Quantitative Determination of the Anomalous Dispersion of Sodium Vapour in the Visible and Ultra-Violet Regions. Philosophical Magazine 8: 293-324
Footnotes
After Thomson, the ratio
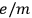 was measured by other physicists, among them Walter Kaufmann. Indeed, Drude referred explicitly to Kaufmann’s measurement of
was measured by other physicists, among them Walter Kaufmann. Indeed, Drude referred explicitly to Kaufmann’s measurement of
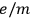 (Kaufmann 1902; 1906).
(Kaufmann 1902; 1906).
The Faraday effect concerns the change in light polarization when light passes through a transparent medium under the action of a constant magnetic field. Indeed, the change in light polarization also depends on the frequency of the light, and this dependence is continuous for the range of the spectrum, except at the absorption frequencies of the material, as in the case of optical dispersion.
Actually, this 1915 paper was the first in which Sommerfeld applied a form of quantization of the atom. But it was not the first time he dealt with optical dispersion. He tackled the issue as early as 1907 and returned to it in 1912 (Sommerfeld 1907; 1912). The goal of these efforts was to remove any doubts about the possibility that light could propagate faster than
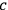 in dispersive media and consequently be in contradiction with certain assumptions of relativity. To that end, he carefully examined the model of Mitschwingungen, applying sophisticated mathematical tools and thereby further illuminated the process of propagation of electromagnetic waves through dispersive media. For more details on Sommerfeld’s scientific activity in Munich, see (Eckert 1993).
in dispersive media and consequently be in contradiction with certain assumptions of relativity. To that end, he carefully examined the model of Mitschwingungen, applying sophisticated mathematical tools and thereby further illuminated the process of propagation of electromagnetic waves through dispersive media. For more details on Sommerfeld’s scientific activity in Munich, see (Eckert 1993).
From the experiments on specific heats performed with
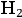 by Arnold Eucken in 1912 (Eucken 1912), it was known that the dependence of the energy of the gas on the temperature was characterized by a proper frequency in the infrared region of the spectrum independent of the instantaneous temperature of the system. This frequency was
by Arnold Eucken in 1912 (Eucken 1912), it was known that the dependence of the energy of the gas on the temperature was characterized by a proper frequency in the infrared region of the spectrum independent of the instantaneous temperature of the system. This frequency was
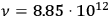 . In 1913, Albert Einsten and Otto Stern (Einstein and Stern 1913), as well as Paul Ehrenfest (Ehrenfest 1913) put forward theoretical accounts of the phenomenon by picturing the molecule as a rotator and quantizing its rotational degrees of freedom. Yet this problem turned out to be unexpectedly difficult, for such a thing as a proper frequency of a rotator does not exist (Gearhart 2010). In 1916, Karl Schwarzschild considered the possibility that rotation combines with the regular precession of the axis of symmetry, thus lifting the degrees of freedom to quantize up to two (Schwarzschild 1916). In the same year, Epstein applied Schwarzschild’s theory to Debye-Sommerfeld’s model of
. In 1913, Albert Einsten and Otto Stern (Einstein and Stern 1913), as well as Paul Ehrenfest (Ehrenfest 1913) put forward theoretical accounts of the phenomenon by picturing the molecule as a rotator and quantizing its rotational degrees of freedom. Yet this problem turned out to be unexpectedly difficult, for such a thing as a proper frequency of a rotator does not exist (Gearhart 2010). In 1916, Karl Schwarzschild considered the possibility that rotation combines with the regular precession of the axis of symmetry, thus lifting the degrees of freedom to quantize up to two (Schwarzschild 1916). In the same year, Epstein applied Schwarzschild’s theory to Debye-Sommerfeld’s model of
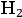 , and realized that it did not led to a good agreement with Eucken’s experiments. To retrieve Ehrenfest’s formula for
, and realized that it did not led to a good agreement with Eucken’s experiments. To retrieve Ehrenfest’s formula for
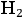 , Epstein had to complicate further the problem, using advanced tools of rotational dynamics, applied to three degrees of freedom, instead of two.
, Epstein had to complicate further the problem, using advanced tools of rotational dynamics, applied to three degrees of freedom, instead of two.
For more information about Ehrenfest’s principle, see (Navarro and Pérez 2006; Pérez 2009).
In 1917, the adiabatic principle also provided Sommerfeld with the conceptual tool to extend the hybrid theory to the explanation of the Faraday effect. By means of the adiabatic principle, Sommerfeld could argue that all modified states produced as a result of the presence of the magnetic field were also stationary states.
Sommerfeld’s new rule enjoyed very little popularity among the experts. Reiche lamented the “unaccountably strange quantum condition” which was “undoubtedly a most unsatisfactory result” (Reiche 1922, 121). Other physicists avoided it completely. For instance, the Austrian physicist Gerda Laski applied the Debye-Sommerfeld theory to different models of molecules more complex than
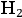 , where valence electrons orbited in two rings, instead of one (Laski 1919). This strategy allowed her to relinquish Sommerfeld’s strange quantum condition for the angular momentum.
, where valence electrons orbited in two rings, instead of one (Laski 1919). This strategy allowed her to relinquish Sommerfeld’s strange quantum condition for the angular momentum.
The reasons why the paper was withdrawn are mentioned in a letter from Bohr to Sommerfeld dated 19 March 1916. There Bohr revealed to Sommerfeld that he had “decided to postpone the publication [of this paper] and consider it all again, in view of all for which your papers [1916 Sommerfeld’s famous papers on the quantum atomic theory] have opened my eyes” (Hoyer 1981, 604).
See the register volume for “Münchener physikalisches Mittwochs-Colloquium,” 1 October 1923. See also AHQP, M/f No. 20, Sect. 001–017.
For a thorough analysis of this development and its role in the emergence of matrix mechanics, see (Duncan and Janssen 2007).
