The quantization of constrained systems is one of the cornerstones of modern elementary dynamical theories. Important fundamental physical theories, such as quantum electrodynamics, quantum chromodynamics, electro-weak unified theory and string theories make use of it. The most widely used, currently canonical formulation for the quantization of constrained Hamiltonian systems was proposed by Paul Dirac in 1950 (Dirac 1950; 1951; 1964), and independently by Peter Bergmann and his collaborators (Bergmann and Brunings 1949; Bergmann et.al. 1950; Anderson and Bergmann 1951). Later, in 1967, Ludvig Fadeev and Victor Popov made important progress in the path-integral quantization of the Yang-Mills field (Fadeev and Popov 1967).
In this paper, we emphasize the contribution of a Chinese theoretical physicist, Professor Tsung-Sui Chang, to this topic. In 1946, Chang pointed out that the previous canonical formulations of constrained systems could not be applied to quantum theory because they did not provide a method for dealing with one of the key features of the analogous classical theories—the appearance of undetermined multipliers. Chang worked out a feasible quantization procedure for such systems.
In the following section, we present a summary of Chang’s education, training, and professional development from the 1930s to his death in 1969. In subsequent sections, we outline theoretical developments in the field leading up to Chang’s own advances.
10.1 Biographical Overview
Chang was born in Hangzhou, Zhejiang Province, on 12 July 1915. He studied physics at Yenching University in 1930, then in 1931 he joined the Physics Department of Tsinghua University, headed by Wu Youxun. It was one of the most prestigious universities in China. In 1934, Chang began a masters degree program under Wu’s supervision. Wu recommended that he continue his training at Cambridge University.
In August of 1936, Chang entered the Mathematics Department of Cambridge University, supported by the Boxer Indemnity. He studied statistical physics as a doctoral student under Ralph Howard Fowler. Chang completed several important works on cooperative phenomena (solid solution, adsorption). The well-known text “Statistical Thermodynamics” by Fowler and Edward Guggenheim (1939) includes a section “The Combinatory Formulae of Chang.”
After receiving his doctorate at Cambridge in 1938, Chang decided to extend his research field beyond statistical physics to quantum field theory. In 1938, Fowler endorsed Chang’s application to Bohr:1
I think I can whole-heartedly recommend him to you. He has done very well in his two years in Cambridge showing very considerable initiative and skill in developing the formal consequences such as order and disorder in alloys. I think you would find him very pleasant to deal with, and thoroughly industrious and able.
In 1939, Chang went to the Theoretical Physics Institute at the University of Copenhagen as a postdoctoral fellow and commenced his research on quantum field theory. His academic career began in earnest with stays at different locations in Europe, including: Copenhagen (September 1938 to February 1939), Zurich (February to June 1939), and Paris (June to October 1939). His acquaintances included Wolfgang Pauli, Niels Bohr and Aage Bohr. In Copenhagen, Chang lived in Bohr’s home and established a very good relationship with Bohr’s family. He completed two articles, “The Azimuthal Dependence of Processes Involving Mesons” (Chang 1940) was published in 1940, then another article on the nature of pseudo-scalar mesons. The latter publication was delayed until 1942 due to Chang’s 1939 return to China and wartime communication difficulties.
Once back in China, Chang became the youngest professor of physics at the National Central University in Chongqing. For the next six years, during the Sino-Japanese War, Chang continued his research on statistical physics and quantum field theory, including the quantization of constrained systems. He published about ten articles during the difficult war period. Meanwhile, he was eager to pursue an international academic exchange. Chang’s hope was fulfilled at the end of 1945 when he had the opportunity to return to Cambridge, thanks to Joseph Needham, who was the head of the Sino-British Science Cooperation Bureau in China, and Dirac. The Bureau provided information and aid for institutions and universities in China in wartime by sending papers to Western journals, offering scientific instruments and sending Chinese scholars to the United Kingdom. During 1944–1946, the Sino-British Science Cooperation Bureau assisted eight Chinese professors in going abroad, including Chang.
In addition to his connection to Bohr, Chang had a close relationship with Dirac, one of Fowler’s previous students. Dirac had already become a well-known professor during Chang’s first visit to Cambridge. Dirac’s research style served as a model for Chang. It was under Dirac’s influence that Chang undertook the study of quantum field theory in 1939. Further, Dirac recommended that Chang teach a Cambridge course on quantum field theory,2 and they had many discussions on this and other topics.
Chang’s first two papers on constrained systems published in Britain were communicated by Dirac, and in the third paper, published in 1947, he thanked Dirac for his interest and discussions.
In the autumn of 1947, Dirac went to the Princeton Institute for Advanced Studies for a short-term visit. He suggested that Chang join him there. Chang spent six months with Dirac in New Jersey. He was then invited to work at the Carnegie Institute of Technology in Pittsburgh, Pennsylvania, for five months.
In the autumn of 1949, Chang left the United States and returned again to China. He successively became a professor in the Physics Department of Peking University, Beijing Normal University and the Institute of Mathematics of the Chinese Academy of Sciences. He also became an academician of the Chinese Academy of Sciences in 1957. He is recognized as one of the founders of quantum field research in China. Despite his successes, he suffered during the Cultural Revolution period and committed suicide on 30 June 1969 at 54 years of age.

Fig. 10.1: Tsung-Sui Chang, 1915–1969, Source: Prof. Yi Ci Chang.
10.2 Studies on Constrained Hamiltonian Systems before Chang’s
Work
10.2.1 Initial Studies
To better understand Chang’s contributions, we now turn to initial studies of constrained systems. The challenge of quantizing a classical constrained dynamical model was present at the birth of quantum field theory. Classical electromagnetism is such a theory, so efforts to describe the quantum interaction of the field with charged particles needed to address the problem of constraints directly. Historically, the first such successful theory, with full quantum electromagnetic interaction, was introduced by Dirac in 1927 (Dirac 1927). With regard to the electromagnetic field itself, Dirac followed a method advanced by Pascual Jordan in 1926 in a joint publication with Born and Heisenberg (Born et.al. 1926). The basic method is to decompose the radiation field into harmonic oscillators, so the quantization of the electromagnetic field was reduced to the quantization of these oscillators. The Dirac scheme dealt exclusively with transverse components of the field and was therefore not obviously relativistically covariant. Subsequently, in 1929, Heisenberg and Pauli established a canonical quantization procedure for general quantum fields (Heisenberg and Pauli 1929; 1930). However, when applying their method to the electromagnetic field, they encountered a stubborn difficulty that was eventually overcome by Heisenberg: the classical momentum conjugate to the scalar potential of electromagnetic fields vanishes identically. This means that the related canonical degrees of freedom were not independent. The canonical variables were subject to constraints. The immediate consequence was the contradictory conclusion that the commutator of this vanishing momentum with the scalar potential would not vanish. Thus, a procedure was needed to avoid this contradiction.
10.2.2 Earlier Approaches to Constrained Systems by Rosenfeld and Dirac
Obvious problems existed in early approaches to the quantization of the
electromagnetic field.3 The first Heisenberg-Pauli method added a new term to the Lagrange function, multiplied by a small parameter
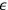 . This had the effect that the momentum no longer vanished. However, the
. This had the effect that the momentum no longer vanished. However, the
 term destroyed the manifest gauge invariance
of the Lagrangian. The second Heisenberg-Pauli method set the scalar potential
term destroyed the manifest gauge invariance
of the Lagrangian. The second Heisenberg-Pauli method set the scalar potential
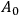 equal to zero, thus destroying manifest Lorentz covariance. Gauss’s law was then imposed as an initial condition on quantum states. In this same paper, they showed that a method that had—in the meantime—been put forth by Fermi was equivalent to adding a Lorenz gauge-fixing term to the Lagrangian, and this gauge condition also needed to be imposed as an initial quantum condition (Fermi 1929; Heisenberg and Pauli 1930).
equal to zero, thus destroying manifest Lorentz covariance. Gauss’s law was then imposed as an initial condition on quantum states. In this same paper, they showed that a method that had—in the meantime—been put forth by Fermi was equivalent to adding a Lorenz gauge-fixing term to the Lagrangian, and this gauge condition also needed to be imposed as an initial quantum condition (Fermi 1929; Heisenberg and Pauli 1930).
Pauli invited the young Rosenfeld to join him in Zurich in 1929 to establish a firmer theoretical foundation for the methods that he, Heisenberg and Fermi had employed in their treatment of quantum electromagnetic field theory. Rosenfeld set himself the task of formulating a Hamiltonian procedure for dealing with local gauge symmetries in the two fundamental interactions that were known at the time, electromagnetism and Einstein’s curved space-time gravitation. From the start he focused on the problem of implementing the full gauge symmetry group as a canonical transformation group acting on the phase space field variables. He made enormous progress in this effort, although his results were largely unknown (or in the case of Dirac, perhaps forgotten) by subsequent researchers. There is no indication that Chang was acquainted with Rosenfeld’s work, although we do know that Dirac was aware of it in 1932 (Salisbury 2009a).
Rosenfeld showed that, as a consequence of local Lagrangian symmetries, identities arise that relate the canonical momenta and configuration variables (when the former are understood as functions of the configuration variables and their time derivatives). Following Rosenfeld, we represent the ensuing constraining relations as
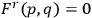 , where the index
, where the index
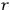 ranges over the total number of such so-called primary constraints. It followed that the time development for given initial conditions was not unique. Furthermore, Rosenfeld showed that this time development could be represented in first-order Hamiltonian form, with a Hamiltonian
ranges over the total number of such so-called primary constraints. It followed that the time development for given initial conditions was not unique. Furthermore, Rosenfeld showed that this time development could be represented in first-order Hamiltonian form, with a Hamiltonian
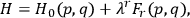
|
10.1 |
where the
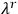 are arbitrary space-time functions.4 The Hamilton equations are then
are arbitrary space-time functions.4 The Hamilton equations are then
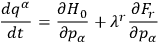
|
10.2 |
and
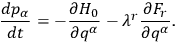
|
10.3 |
Even though Rosenfeld presented an explicitly
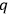 -number version of his formalism in his 1930 article, he did not address the question of how one would or could incorporate the arbitrary functions
-number version of his formalism in his 1930 article, he did not address the question of how one would or could incorporate the arbitrary functions
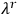 into the quantum theory. However, as pointed out elsewhere (Salisbury 2009a), he had all the tools required to construct gauge invariant objects using his symmetry group generators. In a review of quantum electromagnetism published two years later (Rosenfeld 1932), he simply reverted to the Fermi scheme, after having convinced himself that his prior analysis justified the procedure. Curiously, however, he did not express this conviction in writing.
into the quantum theory. However, as pointed out elsewhere (Salisbury 2009a), he had all the tools required to construct gauge invariant objects using his symmetry group generators. In a review of quantum electromagnetism published two years later (Rosenfeld 1932), he simply reverted to the Fermi scheme, after having convinced himself that his prior analysis justified the procedure. Curiously, however, he did not express this conviction in writing.
In 1933, Dirac published a paper entitled “Homogenous Variables in Classical Dynamics” in which he considered a far narrower class of models than Rosenfeld had examined, not citing him even though it is clear from an exchange of letters in 1932 that Dirac was familiar with Rosenfeld’s work. Dirac wrote in this paper:
The well-known methods of classical mechanics, based on the use of a Lagrangian or Hamiltonian function, are adequate for the treatment of nearly all dynamical systems met with in practice. There are, however, a few exceptional cases to which the ordinary methods are not immediately applicable. For example, the ordinary Hamiltonian method cannot be used when the momenta, defined in terms of the Lagrangian function
by the usual formulae
, are not independent functions of the velocities. (Dirac 1933)
Dirac used the electromagnetic field and the massless relativistic
particle as examples to illustrate his program. The outcome is the same Hamilton equations exhibited by Rosenfeld, with the same arbitrary functions (though designated by Dirac by
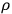 rather than
rather than
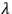 ). Referring to Dirac’s paper, in 1946 Chang observed that the appearance of these arbitrary functions seemed to preclude passage to a quantum theory.
). Referring to Dirac’s paper, in 1946 Chang observed that the appearance of these arbitrary functions seemed to preclude passage to a quantum theory.
10.3 Chang’s Contributions to Hamiltonian Systems
From July 1944 to June 1946, Chang published three papers on the quantization of constrained systems: “A Note on the Hamiltonian Theory of Quantization” (Chang 1945), “A Note on the Hamiltonian Equations of Motion” (Chang 1946), and “A Note on the Hamiltonian Theory of Quantization (II)” (Chang 1947).
The first and second papers were completed under very difficult conditions in Chongqing, a southwestern city in China, during the Sino-Japanese War. They were published in the Proceedings of the Royal Society of London and Proceedings of the Cambridge Philosophical Society, respectively, and were communicated by Dirac. In the second and third papers, Chang expressed his thanks to Dirac for discussions. The third paper, completed at Cambridge University, was the most extensive, summarizing some results from the previous two, and is the principal subject of our analysis. This 1947 paper is divided into three sections in which Chang discusses the need for dealing with the arbitrary functions
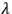 , a proposal for quantizing models in which constraints are imposed at the Lagrangian level through the use of Lagrange multipliers, and a proposal for quantizing systems with primary constraints.
, a proposal for quantizing models in which constraints are imposed at the Lagrangian level through the use of Lagrange multipliers, and a proposal for quantizing systems with primary constraints.
First, Chang observed, in referring to Dirac’s 1933 paper,
The Lagrangian equations for cases with missing momenta have been studied some time ago by Dirac by making use of homogeneous variables. It was shown that the equations of motion can always be put in canonical form. However, the final equations still contain quantities of the nature of unknown Lagrange multipliers, and are thus not suitable for passing to a quantum theory. (Chang 1947)
This may be the first published observation of the challenge that the undetermined functions posed for the canonical quantization program.
10.3.1 Models with Lagrange Multipliers
The first models that Chang considered were models in which constraints were imposed “by hand” through the use of Lagrange multipliers.
He considered systems for which the Lagrangian contained only first
derivatives
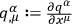 . He supposed that variations of the action
. He supposed that variations of the action
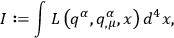
|
10.4 |
were subject to
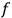 auxiliary conditions
auxiliary conditions
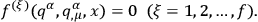
|
10.5 |
Then it followed that
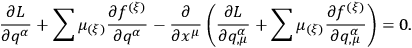
|
10.6 |
Eqs. (10.5) and (10.6) are the field equations. The
Lagrange multipliers
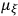 are understood to depend on the space-time coordinates, represented collectively by the symbol
are understood to depend on the space-time coordinates, represented collectively by the symbol
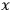 , where we will take them to be real, with
, where we will take them to be real, with
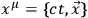 .5
Superscripts
.5
Superscripts
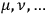 run from 1 to 4, while superscripts
run from 1 to 4, while superscripts
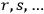 go from 1 to 3. The
go from 1 to 3. The
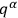 are the dynamical field variables.
are the dynamical field variables.
Chang claimed to have achieved a first-order canonical form for his field equations by first implicitly defining the functions
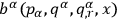 and
and
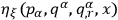 through the relations
through the relations
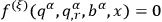
|
10.7 |
and
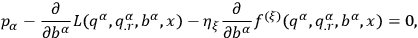
|
10.8 |
where a sum over
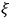 is understood.
He then defined the Hamiltonian to be
is understood.
He then defined the Hamiltonian to be
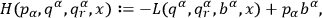
|
10.9 |
where a sum over
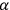 is understood.
is understood.
Using this Hamiltonian function, the canonical equations became
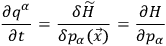
|
10.10 |
and
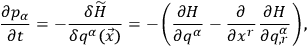
|
10.11 |
where
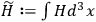 .
.
Substituting for
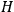 we obtain
we obtain
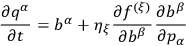
|
10.12 |
and
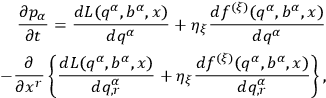
|
10.13 |
where we define the total derivative with respect to
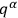 as
as
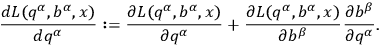
|
10.14 |
Chang claimed that eq. (10.12) yielded
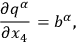
|
failing to mention that this form is achievable only by requiring that
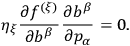
|
He also did not observe that additional restrictions regarding the
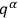 -dependence of the constraining relations (10.5) arise by requiring that the dynamical eq. (10.13) be equivalent to the Euler-Lagrange field eq. (10.6).
-dependence of the constraining relations (10.5) arise by requiring that the dynamical eq. (10.13) be equivalent to the Euler-Lagrange field eq. (10.6).
Generally this means that there are severe limitations to the applicability of Chang’s method. We can, however, give a simple illustrative example in which the procedure may be implemented. We consider a system with
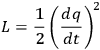
|
and an auxiliary condition
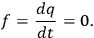
|
Then, employing Chang’s symbols, we have
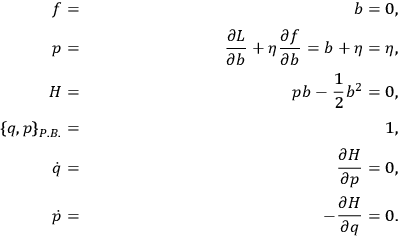
|
We note also that the relevant additional consistency condition that is required to achieve the correct Euler-Lagrange equations is
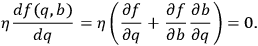
|
10.15 |
This does vanish since
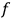 is independent of
is independent of
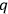 , and
, and
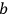 vanishes identically. So although we have a non-trivial model with a Lagrange multiplier that leads to a self-consistent quantum theory here, it is dubious that the procedure could enjoy widespread applicability.
vanishes identically. So although we have a non-trivial model with a Lagrange multiplier that leads to a self-consistent quantum theory here, it is dubious that the procedure could enjoy widespread applicability.
10.3.2 Models with Missing Momenta
Chang next discussed models which possessed missing momenta, i.e., models that in our current terminology have primary
constraints. Chang identified those momenta as “missing”
that vanished due to the absence of the time derivative of the conjugate
configuration variable in the Lagrangian. He assumed that a
transformation of these variables had been undertaken so that all primary
constraints would take this simple form, thus dividing the configuration
variables into a set
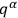 such that the
such that the
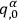 could be
written in terms of the conjugate momenta
could be
written in terms of the conjugate momenta
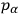 , and another set
, and another set
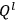 with momenta
with momenta
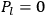 . Chang appears to have been the first to
recognize in print that this decomposition was achievable at the Lagrangian
level, although he did not note that to implement it, it might be necessary
to add total derivative terms to the Lagrangian. Dirac added such terms for general
relativity in 1958 (Dirac 1958).
. Chang appears to have been the first to
recognize in print that this decomposition was achievable at the Lagrangian
level, although he did not note that to implement it, it might be necessary
to add total derivative terms to the Lagrangian. Dirac added such terms for general
relativity in 1958 (Dirac 1958).
In terms of these variables, the Lagrangian field equations take the form
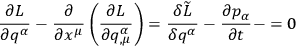
|
10.16 |
and
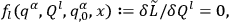
|
10.17 |
where
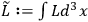 . Thus Chang recognized that the
relations (10.17) were themselves constraints, in addition to the
primary constraints.6
. Thus Chang recognized that the
relations (10.17) were themselves constraints, in addition to the
primary constraints.6
He then presented a procedure about which he explicitly recognized that it was applicable only when the constraints could be employed to eliminate the
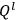 as independent variables. That is, he assumed that the relations
as independent variables. That is, he assumed that the relations
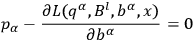
|
10.18 |
and
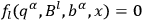
|
10.19 |
could be solved for
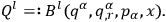
|
10.20 |
Then under these circumstances, the Hamiltonian
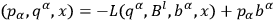
|
10.21 |
delivers
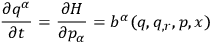
|
10.22 |
and
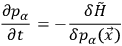
|
10.23 |
and is equivalent to the original Lagrangian field equations.
Thus Chang recognized correctly that systems may exist where the constraints can be solved. And in this case, upon passing to the quantum theory, one can have canonical Hamiltonian equations and
commutation relations just for the independent variables
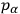 and
and
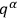 with the
with the
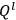 becoming functions of
becoming functions of
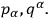 He did not observe that this circumstance arises when the constraints have non-vanishing Poisson brackets among themselves, or in the language that was introduced by Dirac in 1950, when the constraints are second class (Dirac 1950).
He did not observe that this circumstance arises when the constraints have non-vanishing Poisson brackets among themselves, or in the language that was introduced by Dirac in 1950, when the constraints are second class (Dirac 1950).
The models for which the constraints cannot be solved belong to another type. Chang also discussed a limited version of this case, which we address in the next subsection. This is the situation with gauge theories for which the constraints do have vanishing Poission brackets among themselves. Dirac called such constraints first class. So although Chang did not characterize them in this way, he was certainly aware that there existed two kinds of constrained systems, and he presented a preliminary procedure for quantizing them.
Dirac was one of the first to propose a quantization procedure that dealt with both types. In gauge theories, he noted that gauge conditions need to be invoked, and he introduced modified brackets that respected these conditions (Dirac 1950). It seems likely that Chang’s work would have influenced Dirac’s movement in this direction.
10.3.3 Gauge Covariant Models
Having realized that his program for second class constraints did not work
for systems like electromagnetism, Chang then embarked on an alternate
approach. He considered a system in which the Lagrangian
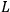 is such that some
of the
is such that some
of the
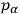 are missing, but with the assumption that
are missing, but with the assumption that
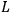 is increased by an
amount
is increased by an
amount
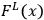 under the transformation
under the transformation
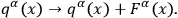
|
We represent the resulting variations with the symbol
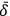 ,
writing
,
writing
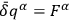 . The resulting variation of
the Lagrangian is
. The resulting variation of
the Lagrangian is
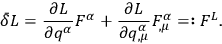
|
10.24 |
Chang remarks that the variation he is considering “is not the same as an ordinary gauge transformation,” but he calls it a gauge transformation “for lack of a better name.” Yet he does assume that his Euler-Lagrange equations are covariant under this transformation. This result follows immediately from the assumption that
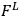 is a function only of
is a function only of
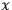 (and not of the dynamical variables). He is perhaps assuming, at least initially, that the
(and not of the dynamical variables). He is perhaps assuming, at least initially, that the
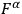 do not depend on arbitrary space-time functions. Also, general gauge transformations have a dependence on the dynamical variable, i.e.,
do not depend on arbitrary space-time functions. Also, general gauge transformations have a dependence on the dynamical variable, i.e.,
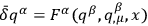 . Such is the case, for example, with general relativity and also with the homogeneous models that were treated by Dirac (1933). In any case, the electromagnetic model that he cites specifically as susceptible to his analysis is clearly gauge covariant in the current sense.
. Such is the case, for example, with general relativity and also with the homogeneous models that were treated by Dirac (1933). In any case, the electromagnetic model that he cites specifically as susceptible to his analysis is clearly gauge covariant in the current sense.
Next, Chang points out that when the field equations are satisfied, one obtains, after performing a spatial integration by parts and letting the gauge variations vanish at spatial infinity,
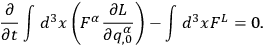
|
10.25 |
At this point, Chang assumes that the
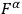 involve arbitary
functions
involve arbitary
functions
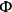 of the time up to order
of the time up to order
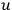 , and this leads him to a
remarkable result: it follows from eq. (10.25) that the coefficients of
each order of time derivative must separately vanish. This result was
already known, to be sure, to Rosenfeld in 1930—but it was independently
rediscovered in 1951 by James L. Anderson and Bergmann and is generally attributed to
them (Anderson and Bergmann 1951). Indeed, these authors introduced the
terminology that is still in use today. The requirement that primary constraints
be preserved under time evolution may lead to secondary
constraints. These in turn may lead to tertiary
constraints, and so on.
, and this leads him to a
remarkable result: it follows from eq. (10.25) that the coefficients of
each order of time derivative must separately vanish. This result was
already known, to be sure, to Rosenfeld in 1930—but it was independently
rediscovered in 1951 by James L. Anderson and Bergmann and is generally attributed to
them (Anderson and Bergmann 1951). Indeed, these authors introduced the
terminology that is still in use today. The requirement that primary constraints
be preserved under time evolution may lead to secondary
constraints. These in turn may lead to tertiary
constraints, and so on.
Chang notes that the highest derivative term,
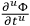 , that appears in eq. (10.25) will not involve a time
derivative of momenta. This term is
, that appears in eq. (10.25) will not involve a time
derivative of momenta. This term is
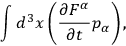
|
10.26 |
and isolating the coefficient of
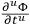 in the integrand, we deduce the existence of primary constraints that Chang
represents as
in the integrand, we deduce the existence of primary constraints that Chang
represents as
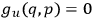 . But then the coefficient of
. But then the coefficient of
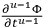 will be in the form
will be in the form
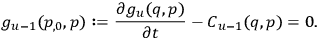
|
10.27 |
In other words, the preservation of the primary constraint requires the
existence of a secondary constraint
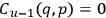 , and so on. Thus eq. (10.25) may be rewritten as
, and so on. Thus eq. (10.25) may be rewritten as
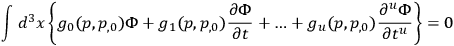
|
10.28 |
with
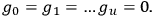
|
10.29 |
Actually, Chang did not state explicitly that constraints
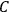 would
arise, but it is an immediate consequence of the relation (10.25).
would
arise, but it is an immediate consequence of the relation (10.25).
Although Chang did not provide a concrete example, it is instructive to take the electromagnetic field as an example to illustrate his formulation—and identify one shortcoming. As mentioned above, Chang did note that the electromagnetic model satisfied his assumptions regarding the gauge invariance of the Lagrangian. This is true, provided that the charged source current is understood to be a non-dynamical external field, as we highlight below.
The Lagrangian for this model is
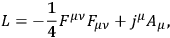
|
10.30 |
where
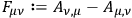
|
10.31 |
and
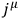 is an external current.
Then the conjugate momenta are
is an external current.
Then the conjugate momenta are
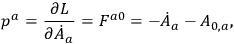
|
10.32 |
while
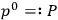 vanishes identically.
vanishes identically.
The Lagrangian equations of motion are
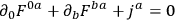
|
10.33 |
and
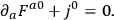
|
10.34 |
The gauge variation is

|
10.35 |
The variation of the Lagrangian under this transformation is
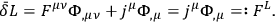
|
10.36 |
Thus, provided that
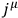 is a prescribed function of
is a prescribed function of
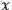 , the variation
may be written as a total time derivative, and the variation is a true gauge
transformation.
, the variation
may be written as a total time derivative, and the variation is a true gauge
transformation.
Performing integrations by parts of the action, and letting the variations vanish at spatial infinity, we find that if the equations of motion are satisfied, then
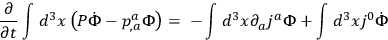
|
10.37 |
or
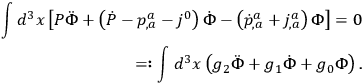
|
10.38 |
Thus, the Gauss’s law constraint
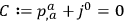 may be a consequence of the required vanishing of the time derivative
of the primary constraint
may be a consequence of the required vanishing of the time derivative
of the primary constraint
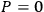 .
.
Chang showed generally that the consistency conditions (10.38) guarantee that if the equation of motion
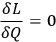
|
10.39 |
is fulfilled at the initial time, then it is fulfilled for all time. For the electromagnetic example, this means that if
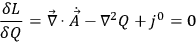
|
10.40 |
is fulfilled at an initial time, then it will be fulfilled at all future
times. Chang therefore proposes that the variables
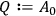 and
and
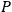 can be
eliminated entirely by setting
can be
eliminated entirely by setting
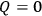 , and therefore setting as an initial
condition
, and therefore setting as an initial
condition
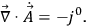
|
10.41 |
Finally in passing to the quantum theory, he imposes this classical initial
condition as a condition on the quantum state
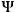 ,
,
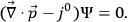
|
10.42 |
So the ultimate practical outcome of this analysis for quantum electrodynamics is that Chang provided another, somewhat more general proof of the legitimacy of the second quantization procedure proposed by Heisenberg and Pauli (1930).
10.4 Conclusion
In summary, we have identified the following five original contributions of Chang to the quantization of constrained systems:
1He was the first to recognize in print, and to offer a preliminary resolution of, a problem for quantization posed by the appearance of arbitrary space-time functions in classical gauge theories.
2Chang proposed a procedure for imposing quantum constraints, using Lagrangian multipliers, for a limited class of non-singular classical theories.
3He recognized that constrained systems could exist in which the constraints could be solved, thereby entirely eliminating some canonical degrees of freedom. Canonical Poisson bracket relations of the remaining phase space variables could then be replaced by canonical quantum commutation relations. Furthermore, he showed that in these models, the functions that multiply the constraints become functions of the dynamical variables, and that they therefore become non-trivial operators in quantum theory. Dirac later discovered that these models possessed the property that the Poisson brackets of the constraints among themselves did not vanish.
4He discovered for a limited class of classical gauge theories that the preservation of primary constraints under time evolution leads to additional constraints. This discovery has until recently been attributed to Anderson and Bergmann in 1951, even though the general proof was already demonstrated by Rosenfeld in 1930.
5Chang developed a technique for quantizing a class of gauge covariant models that could be viewed in the case of electromagnetism as a somewhat more general proof of the legitimacy of the quantization procedure proposed by Heisenberg and Pauli in 1930. This method formulates the gauge condition as a restriction on initial quantum states.
There is a clear link between Chang’s activities during 1945–1947 and Dirac’s subsequent publications beginning three years later on constrained Hamiltonian systems. In future work, we intend to further investigate the detailed manner in which they influenced each other.
Abbreviations and Archives
| Niels Bohr Archive | Bohr Scientific Correspondence, Fowler to Bohr. Folder 19. No. 380608 |
| Cambridge University Reporter | Reporter issues for the academic year 1936–1937, Vol. 67; 1937–1938, Vol. 68 |
Acknowledgements
Xiaodong Yin was supported by NSFC under No.11075109. We would like to express our gratitude to the academician of the Chinese Academy of Science, Professor Yuanben Dai, for his detailed discussions.
List of Chang’s Publications
Papers in English in International Journals:
(1937) An Extension of Bethe’s Theory of Order-Disorder Transitions in Metallic Alloys, Proceedings of the Royal Society A, 161, 546–563.
(1937) Specific Heats of Solids due to Molecular Rotation, Proceedings of the Cambridge Philosophical Society, 33, 524–533.
(1938) Superlattice Formations of the Type AB in Alloys with Applications to the Theory of Adsorption, Proceedings of the Cambridge Philosophical Society, 34, 224–237.
(1939) Statistical Theory of the Adsorption of Double Molecules, Proceedings of the Royal Society A, 169, 512–531.
(1939) The Number of Configurations of an Assembly with Long-Distance Order, Proceedings of the Royal Society A, 173, 48–58.
(1939) Superlattice Formation of the Type AB in an Adsorbed Layer, Proceedings of the Cambridge Philosophical Society, 35, 70–83.
(1939) The Number of Configurations in an Assembly and Cooperative Phenomena, Proceedings of the Cambridge Philosophical Society, 35, 265–292.
(1940) The Azimuthal Dependence of Processes Involving Mesons, Proceedings of the Cambridge Philosophical Society, 36, 34–42.
(1941) A Note on Bethe-Kirkwood’s Partition Function of a Binary Solid Solution, Journal of Chemical Physics, 9, 169–174.
(1941) Second Neighbour Interactions and the Critical Behaviours of Binary Solid Solution, Journal of Chemical Physics, 9, 174–176.
(1942) Arrangements with Given Number of Neighbours (and C. C. Ho), Proceedings of the Royal Society A, 180, 345–365.
(1942) Properties of Mesons Described by a Pseudo-Scalar Wave Function, Det Kongelige Danske Videnskabernes Selskab Mathematisk-Fysiske Meddelelser, 19, 17–19.
(1943) Arrangements of Double Molecules on a Lattice, (and S. K. Kao), Transactions of the Faraday Society, 39, 288.
(1944) The Impulse-Energy Tensor of Material Particles, I. Mesons and Electrons, Proceedings of the Royal Society A, 182, 302–318.
(1945) A Note on the Hamiltonian Theory of Quantization, Proceedings of the Royal Society A, 183, 316–328.
(1946) A Note on the Hamiltonian Equations of Motion, Proceedings of the Cambridge Philosophical Society, 42, 132–138 .
(1946) Quantum Electrodynamics with
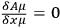 , Proceedings of the Royal Society A, 185, 192–206.
, Proceedings of the Royal Society A, 185, 192–206.
(1947) A Note on the Hamiltonian Theory of Quantization (II), Proceedings of the Cambridge Philosophical Society, 43, 196–204.
(1947) A Note on Relativistic Second Quantization, Proceedings of the Cambridge Philosophical Society, 43, 183–195.
(1948) Field Theories with High Derivatives, Proceedings of the Cambridge Philosophical Society, 44, 76–86.
(1948) Surface Effects in Cooperative Phenomena, Proceedings of the Cambridge Philosophical Society, 44, 598–600.
(1949) Relativitic Field Theories, Physical Review, 75, 967.
(1950) The Quantum Mechanics of Localizable Dynamical Systems, Physical Review, 78, 592.
Papers in Chinese, English and Russian in Chinese Journals:
(1948) Remarks on the Theory of S Matrices, National Peking University Semi-Centennial Papers, 81–88.
(1949) On Weiss’ Theory of Fields, Chinese Journal of Physics, 7, 265–27 (in English).
(1951) Relativistic Nature of Coulombian Interaction, Chinese Journal of Physics, 8, 123–130.
(1953) Calculations of Some Operators in Relativistic Quantum Mechanics, Part I, Acta Mathematica Sinica, 3, 59–72.
(1953) Calculations of Some Operators in Relativistic Quantum Mechanics, Part II, Acta Mathematica Sinica, 3, 73–85.
(1954) A Remark on Boltzmann H Theorem, Acta Physica Sinica, 10, 1–12.
(1956) A Remark on the Application of Mayer’s Theory of Imperfect Gases to Regular Solid Solutions, Acta Physica Sinica, 12, 379–398.
(1956) Classical Motion of Material Particles, Journal of Beijing Normal University, 1, 1–13.
(1956) Direct Calculations of Spinor Matrices, Journal of Beijing Normal University, 1, 15–18.
(1956) Reduction of Canonical Equations, Acta Physica Sinica, 12, 393–401.
(1957) Free Energy of a Solid Solution on a Face-Centered Cubic Lattice (and H. C. Ting, T. K. Tsiao), Acta Physica Sinica, 13, 515–524.
(1957) Note on Quantum Electrodynamics with High Derivatives, Journal of Beijing Normal University, 2, 53–60.
(1957) Configurational Partition Function of Binary Solid Solutions, (and T. M. Wang, H. C. Hsu), Acta Physica Sinica, 13, 525–542.
(1958) A Note on Interactions Representation, Science Record, 2, 250 (in English).
(1958) A New Approximate Method of Constructing Configurational Partition Functions of Cooperative Assembles, Scientia Sinica, 7, 313.
(1958) Some Account of Works of H. H. Bogoliubov and E. Lifshitz, Acta Physica Sinica, 14, 274–279.
(1958) High Order Equations in Quantum Theory, Acta Physica Sinica, 14, 307.
(1958) Normal Dependent Terms in Wave Equations in Interaction Representation, Acta Physica Sinica, 14, 308.
(1958) A Note on the Ergodic Theorem for Quantized Systems, Acta Physica Sinica, 14, 400–404.
(1958) Some Remarks on the Theory of Expansors, Acta Physica Sinica, 14, 405–422.
(1959) The Configurational Partition Functions of Solid Solutions, Acta Physica Sinica, 15, 42–54.
(1959) A Simplified Proof of Dispersive Relations, Acta Physica Sinica, 15, 609–615.
(1959) Remarks on Chew-Low Equations, Acta Physica Sinica, 15, 616–623.
(1959) Regular Solutions With Molecules Occupying Several Sites, Acta Physica Sinica, 15, 652–663.
(1959) Configurational Partition Function for Regular Solid Solutions, Scientia Sinica, 8, 401.
(1961) Analyticity of Perturbation Expansions, Acta Physica Sinica, 17, 1–17.
(1961) Integral Representations of Commutators, Acta Physica Sinica, 17, 163–169.
(1962) Analyticity of Perturbation Expansions, Acta Physica Sinica, 18, 91–117.
(1964) Asymptotic Behavior of a Ladder, Acta Physica Sinica, 20, 378–380.
(1964) Inelastic Amplitudes in the Lee Model Possessing Crossing Symmetries, Acta Physica Sinica, 20, 1090–1100.
(1965) The Regge Cuts in a Perturbation Theory, Acta Physica Sinica, 21, 1381.
(1965) On Singularities of Amplitudes in a Perturbation Theory (and F. T. Wu, T. C. Jiu), Acta Physica Sinica, 21, 1544–1551.
(1965) Motion of Poles in the Lee Model, Acta Physica Sinica, 21, 1882–1888.
Dissertation (at Cambridge University):
(1938) Applications of Bethe’s Method in Statistical Mechanics, Cambridge University
References
Anderson, James L., Peter G. Bergmann (1951). Constraints in Covariant Field Theories. Physical Review 83: 1018-1025
Bergmann, Peter G., Johanna H. M. Brunings (1949). Non-linear Field Theories II. Canonical Equations and Quantization. Reviews of Modern Physics 21: 480-487
Bergmann, Peter G., Robert Penfield, R. P., Schiller Robert (1950). The Hamiltonian of the General Theory of Relativity with Electromagnetic Field. Physical Review 80: 81-88
Born, Max, Pascual Jordan, P. J. (1926). Zur Quantenmechanik II. Zeitschrift für Physik 35: 557-615
Chang, Tsung-Sui (1940). The Azimuthal Dependence of Processes Involving Mesons. Proceedings of the Cambridge Philosophical Society 36: 34-42
- (1945). A Note on the Hamiltonian Theory of Quantization. Proceedings of the Royal Society A 183(994): 316-328
- (1946). A Note on the Hamilton Equations of Motion. Proceedings of the Cambridge Philosophical Society 42: 132-138
- (1947). A Note on the Hamiltonian Theory of Quantization II. Proceedings of the Cambridge Philosophical Society 43: 196-204
Dirac, Paul A. M. (1927). The Quantum Theory of the Emission and Absorption of Radiation. Proceedings of the Royal Society A 114: 243-265
- (1933). Homogeneous Variables in Classical Dynamics. Proceedings of the Cambridge Philosophical Society 29: 389-401
- (1950). Generalized Hamiltonian Dynamics. Canadian Journal of Mathematics 2: 129-148
- (1951). The Hamiltonian Form of Field Dynamics. Canadian Journal of Mathematics 3: 1-23
- (1958). The Theory of Gravitation in Hamiltonian Form. Proceedings of the Royal Society A 246: 333-343
- (1964). Lectures on Quantum Mechanics. New York: Yeshiva University Press.
Fadeev, Ludvig, Victor Popov (1967). Feynman Diagrams for the Yang-Mills Field. Physics Letters B 25: 29-30
Fermi, Enrico (1929). Sopra l'elettrodinamica quantistica. Rendiconti Lincei 9: 881-887
Fowler, Ralph H., Edward A. Guggenheim (1939). Statistical Thermodynamics. Cambridge: Cambridge University Press.
Heisenberg, Werner, Wolfgang Pauli (1929). Zur Quantendynamik der Wellenfelder. Zeitschrift für Physik 56: 1-61
- (1930). Zur Quantentheorie der Wellenfelder II. Zeitschrift für Physik 59: 168-190
Rosenfeld, Léon (1930). Zur Quantelung der Wellenfelder. Annalen der Physik 5: 113-152
- (1932). La théorie quantique des champs. Annales de l'Institut Henri Poincaré 2: 25-91
Salisbury, Donald (2009a). Léon Rosenfeld and the Challenge of the Vanishing Momentum in Quantum Electrodynamics. Studies in History and Philosophy of Modern Physics 40: 363-373
- (2009b). Translation and Commentary of Léon Rosenfeld's “Zur Quantelung der Wellenfelder”, Annalen der Physik 397, 113 (1930). Max Planck Institute for the History of Science
Footnotes
Correspondence by Fowler to Bohr on 8 June 1938, Niels Bohr Archive.
Cambridge University Reporter, Reporter issues for the academic year 1936–1937, Vol. 67, 682; 1937–1938, Vol. 68, 633.
See (Salisbury 2009a) for a detailed analysis.
We assume here for the sake of simplicity that the number of physical variables
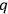 is finite. The extension to field theory is straightforward.
is finite. The extension to field theory is straightforward.
Chang used
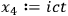 .
.
In the following section, Chang showed that in gauge covariant models these constraints arise due to the demand that primary constraints be preserved under time evolution.
