In 1900, Max Planck (1858–1947) obtained his famous radiation formula, see eq. (4.1) (Planck 1913, §156, eq. 275), for the energy per volume and frequency interval emitted by a black body by rather “obscure means” (Darrigol 2009):
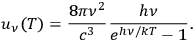
|
4.1 |
This fitted perfectly with the data over the whole frequency-temperature range investigated at that time (Warburg 1913; Rubens 1913). The way Planck found this formula, partly by “ingenious mathematical manipulations” (Cassidy 2005), how he was driven to the assumption and, later on, to the acceptance of the discrete energy quanta of the oscillators within his model black-body radiator has been related so many times that we may disregard it here.1 We would like to comment here that the derivation of the two factors in eq. (4.1) show quite different problems. The first factor is connected to the dynamics of the oscillators within a black-body radiator; the second derives from the combinatorial assumptions of how energy elements are distributed over resonators. Its various forms and the related controversies were discussed extensively in publications by Olivier Darrigol (1988; 1991). Satyendranath Bose (1894–1974) was the first to put both factors on equal footing (Bose 1924).
In what follows, we concentrate exclusively on the interpretation, not the derivation, of the second factor in eq. (4.1) in terms of light particle concepts. Albert Einstein (1879–1955) opened discussion on the particle nature of black-body radiation as early as 1905 (Einstein 1905). In discussing the entropy of a black body as function of volume, he showed that black-body radiation behaves in the Wien limit like a diluted gas consisting of light quanta. The energy of light appeared in some kind of “granular structure” (Darrigol 1988, 20). Here, we will mainly follow the historical development of the light atom and light molecule concepts, giving some emphasis to the two main actors, Mieczysław Wolfke (1883–1947) and Walther Bothe (1891–1957), as well as to their relationships with Planck, Einstein, Max von Laue (1879–1960) and Louis de Broglie (1892–1987). The early part of this story, up to the beginning of the 1920s, has already been dealt with in part by Silvio Bergia and Darrigol (Bergia et.al. 1985; Darrigol 1988; 1991).
4.1 First Corpuscular Concepts of Light
Einstein always denied interpreting light in general as being composed of independent quanta. In a letter to Hendrik A. Lorentz (1853–1928) dated 23 May 1909, Einstein writes:
[…] I am not at all of the opinion that light has to be thought of as being composed of mutually independent quanta localized in relatively small spaces. To be sure, that would be the most convenient way to explain the Wien end of the radiation formula. But the splitting of light rays on the surface of refracting media already makes this approach absolutely inadmissible. A light ray splits, but a light quantum cannot split without a change in frequency. (Klein et.al. 1993, 193; for German original see: Klein et.al. 1993, 123)2
In his 1916 and 1917 papers, “Zur Quantentheorie der Strahlung,” (Einstein 1916; 1917)3 Einstein showed that, analogous to particles, each light quantum in a radiation bundle carries a momentum of
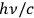 . However, before Einstein, a number of researchers had already understood these as real atoms.
An early summary of these activities can be found in Harry Bateman’s (1882–1946) 1923 publication (Bateman 1923).
. However, before Einstein, a number of researchers had already understood these as real atoms.
An early summary of these activities can be found in Harry Bateman’s (1882–1946) 1923 publication (Bateman 1923).
On 27 September 1910 Abram F. Ioffe (1880–1960) presented a talk, “Zur Theorie der Strahlungserscheinungen” (Ioffe 1911), at a meeting of the Physical Division of the Russian Physico-Chemical Society, the content of which he had already discussed a few weeks earlier with Planck.4
[…] He [Planck] deemed my article interesting. However, he urgently insisted that I abandon the use of photons since they are inconsistent with Maxwell’s electromagnetic theory of light. (Ioffe 1983, 63)
In his reminiscences, Ioffe used the term “photon,” even though it was introduced in 1926 by Lewis (Lewis 1926). Nevertheless, it was published somewhat later in Annalen der Physik of which Planck was an editor. During his visit, Planck had assured Ioffe:
[…] that he will not oppose the publication of the manuscript. However, he does not intend to ruin with his own hands the principles of Maxwell’s construct. For him personally, the manuscript is certainly lamentable […]. (Ioffe 1985, 425)
The headline of the second part of this publication (Ioffe 1911) “Atomistische Struktur der Strahlung” and the headline of §2 “Strahlungsquanten” both point toward an interpretation of light in terms of an atomistic concept. Indeed, §2 in part two starts with the sentence:
Since the appearance of Einstein’s article a series of facts have been discovered and discussed, which find their simplest explanation in an atomistic concept of radiation, or at least of its emission.5 (Ioffe 1911, 546–547)
A list of seven points supporting this claim followed.
Around the same time, Johannes Stark (1874–1957) tried to gain experimental insight into the description of X-rays as light quanta, or alternatively as ether waves (Stark 1910).6 Theoretically, he discussed the momentum conservation in electron collisions with matter in great detail.7 Experimentally, he analyzed the forward-backward asymmetry of X-rays emitted in electron collisions on a thin, low Z anode (charcoal). In formulating the conditions for momentum conservation under the assumption that the X-rays are light quanta, he explicitly used a vector of length
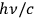 for the momentum of the emitted X-rays and predicted a pronounced forward-backward asymmetry of their momentum (energy) and intensity distributions.
In contrast, if X-rays were ether-waves, he found that electrodynamics demanded an isotropic distribution (Abraham 1905).
The very demanding experiment revealed pronounced forward-backward asymmetries in X-ray intensities and energies, clearly favoring the light-quantum hypothesis.8
for the momentum of the emitted X-rays and predicted a pronounced forward-backward asymmetry of their momentum (energy) and intensity distributions.
In contrast, if X-rays were ether-waves, he found that electrodynamics demanded an isotropic distribution (Abraham 1905).
The very demanding experiment revealed pronounced forward-backward asymmetries in X-ray intensities and energies, clearly favoring the light-quantum hypothesis.8
In 1913, Wolfke, at the time a Privatdozent (private lecturer) in Zurich, was probably the first to introduce the item “light atom” (Lichtatom) as a center with energy
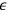 , referring to Stark and to Einstein’s 1905 article (Stark 1910; Einstein 1905; Wolfke 1913a). Light energy
, referring to Stark and to Einstein’s 1905 article (Stark 1910; Einstein 1905; Wolfke 1913a). Light energy
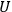 was thought to be localized in a large but finite number
was thought to be localized in a large but finite number
 of these centers:
of these centers:
|
4.2 |
Wolfke chose the term “light atom” to indicate that they cannot come into existence or decay by themselves, for example,
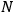 stays constant when reflected off a moving, perfect mirror. He then used this hypothesis to derive the dispersion relation for light atoms with the following arguments: according to classical electrodynamics, the ratios of beam energies
stays constant when reflected off a moving, perfect mirror. He then used this hypothesis to derive the dispersion relation for light atoms with the following arguments: according to classical electrodynamics, the ratios of beam energies
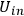 and
and
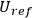 and of the frequencies
and of the frequencies
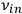 and
and
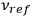 for an incoming and reflected beam of light respectively, are identical, see (Abraham 1905, §40; Planck 1913, §77, eqs. 86/87). Thus
for an incoming and reflected beam of light respectively, are identical, see (Abraham 1905, §40; Planck 1913, §77, eqs. 86/87). Thus
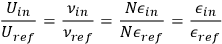
|
4.3 |
follows, since the number of light atoms
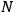 in a beam ought not to change while the beam is reflected from a perfect mirror. Therefore,
in a beam ought not to change while the beam is reflected from a perfect mirror. Therefore,
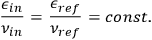
|
4.4 |
The light atoms thus follow the dispersion relation
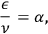
|
4.5 |
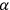 being a universal constant.9 Wolfke commented on this result as follows: “The equation forms the main equation of the light atom”10 (Wolfke 1913a, 1125).
being a universal constant.9 Wolfke commented on this result as follows: “The equation forms the main equation of the light atom”10 (Wolfke 1913a, 1125).
Using this atomistic picture of light, Wolfke interpreted radiation pressure as being caused by the hits of light atoms on a mirror (Wolfke 1913b). In doing so, he allocated a mass to a light atom of energy
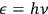 via the relativistic relation
via the relativistic relation
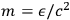 for the first time. Before arriving at the heart of the problem, he related the number of light atoms per unit time and volume to the power (energy per time) of the light beam. Then he used a formula found in Planck’s book on heat radiation (Planck 1913, §60, 58, uppermost formula). It connected the radiation pressure
for the first time. Before arriving at the heart of the problem, he related the number of light atoms per unit time and volume to the power (energy per time) of the light beam. Then he used a formula found in Planck’s book on heat radiation (Planck 1913, §60, 58, uppermost formula). It connected the radiation pressure
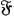 , with the number of light atoms hitting the mirror per unit area, with their allotted mass
, with the number of light atoms hitting the mirror per unit area, with their allotted mass
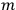 and with the scattering angle
and with the scattering angle
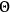 . This formula was obtained by Planck in a quantum picture of light assuming correctly
. This formula was obtained by Planck in a quantum picture of light assuming correctly
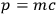 for the momentum of a light quantum.11 Wolfke finally eliminated the mass through the correct relativistic relation
for the momentum of a light quantum.11 Wolfke finally eliminated the mass through the correct relativistic relation
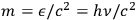 and arrived thus within a quantum picture of light at the classical relation
and arrived thus within a quantum picture of light at the classical relation
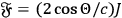 between radiation pressure
between radiation pressure
 and light power
and light power
 .
.
At this point, we pause to present Wolfke’s involvement up until 1920 in the “light atom” concept in further detail, in particular his controversy with Yurij Aleksandrovich Krutkov (1890–1952), Paul Ehrenfest’s (1886–1930) pupil in St. Petersburg and at that time his visitor in Leiden (Frenkel 1971). This involvement did not lead to any considerable insight and was discussed in detail by Darrigol (1991, 254–255), as well as by Luis Navarro and Enric Perez (2004, 130–132).
First, we briefly report on Wolfke’s background.12 Wolfke was a native Pole. Under Otto R. Lummer (1860–1925), he received a doctorate in Breslau in 1910 with a dissertation on optics (Wolfke 1911). At the beginning of 1913, Wolfke moved to the Eidgenössische Technische Hochschule (ETH)13 in Zurich. He must have soon met Einstein, since Einstein served as referee in Wolfke’s Habilitationskommission (habilitation committee) (Wolfke 1980). On the basis of a publication that had already appeared in 1912 in Annalen der Physik (Wolfke 1912), as well as of the positive appraisal of his personality and abilities by Einstein and others,14 he was promoted on 8 May 1913 to Privatdozent at the ETH.
According to a personal report of his son Karol Wolfke, Einstein often visited the Wolfkes and “played violin with father’s piano accompaniment” (Sredniawa 2006, 261). It is thus rather probable that Wolfke discussed the light quantum problems with Einstein. And indeed Wolfke notes in one of his publications, at the time of his debate with Krutkov, that Einstein brought certain facts to his attention (Wolfke 1914b). This hypothesis is corroborated by several remarks by Darrigol, indicating that Einstein supported Wolfke in his struggle with Krutkov (Darrigol 1991, 254–259).

Fig. 4.1: Mieczysław Wolfke. Courtesy of the Archives of the Polish Academy of Sciences (APAN).
In the fall of 1922, Wolfke became a professor of physics at the Technical University in Warsaw. There, he worked experimentally on a variety of problems concerning optics, high voltages, properties of liquid helium, and obviously also on what he called “light molecules.” From a report in Nature on the Fifth Congress of Polish Physicists in Poznań (Anonymous 1930, 660), we learn that Wolfke presided over the congress, and we read further that “special interest was aroused by papers on association of light quanta by Wolfke.”
4.2 Light Molecules, Static Concepts
4.2.1 Wolfke 1921
At the beginning of 1914, Wolfke published a brief third note, entitled “Zur Quantentheorie” (Wolfke 1914a), within a series of papers released in Verhandlungen der DPG. Here, he speculated qualitatively on how the transition from the classical Rayleigh-Jeans limit (large radiation density) to the Wien limit (small radiation density) could proceed. A few years later while still in Zurich, he resumed this topic.15 In a publication entitled “Einsteins Lichtquanten und die räumliche Struktur der Strahlung”, he intended to demonstrate that “[…] black-body radiation […] consists of thermodynamically-independent parts […]”16 (Wolfke 1921, 378) with energy density contents of
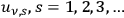 .17
.17
His starting point was the then well-known identity for the energy density per unit frequency interval in Planck’s formula, see eq. (4.1)
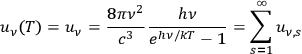
|
4.6 |
with
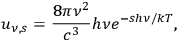
|
4.7 |
Using this expansion and generalizing Einstein’s method from the 1905 paper (Einstein 1905) to the full radiation spectrum, Wolfke showed that the sum of the partial entropy densities
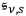 calculated for the partial energy densities
calculated for the partial energy densities
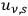 adds up to the well-known expression for the entropy density of black-body radiation
adds up to the well-known expression for the entropy density of black-body radiation
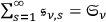 . Thus he interpreted the partial radiation densities
. Thus he interpreted the partial radiation densities
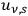 as thermodynamically independent of each other.
as thermodynamically independent of each other.
For a black body of volume
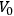 ,
,
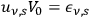 may denote the energy per frequency interval of the
may denote the energy per frequency interval of the
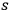 th partial radiation. Following Einstein’s methodological tools, Wolfke obtained this radiation energy for the probability
th partial radiation. Following Einstein’s methodological tools, Wolfke obtained this radiation energy for the probability
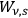 within a subvolume,
within a subvolume,
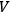
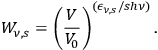
|
4.8 |
He therefore interpreted this relation such that the
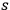 th partial wave consists of
th partial wave consists of
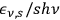 spatially independent radiation quanta
spatially independent radiation quanta
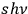 . He named these objects light molecules and finished his considerations with the remark:
. He named these objects light molecules and finished his considerations with the remark:
[…] that black-body radiation, as seen from the point of view of Einstein’s light-quantum hypothesis, consists of spatially independent light molecules,
,
[…].20 (Wolfke 1921, 378)
Finally, Wolfke analyzed the number density
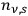 of light molecules per unit frequency interval:21
of light molecules per unit frequency interval:21
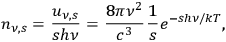
|
4.9 |
yielding for the ratio of successive number densities:22
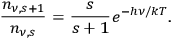
|
4.10 |
For large values of
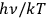 (Wien limit), the ratio
(Wien limit), the ratio
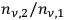 becomes very small in comparison to 1. Thus the radiation field consists of independent light quanta (light atoms) only, as stated by Einstein in his 1905 paper (Einstein 1905). Approaching the classical Rayleigh-Jeans limit with decreasing values of
becomes very small in comparison to 1. Thus the radiation field consists of independent light quanta (light atoms) only, as stated by Einstein in his 1905 paper (Einstein 1905). Approaching the classical Rayleigh-Jeans limit with decreasing values of
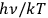 , the ratios
, the ratios
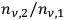 increase. Wolfke concluded:
increase. Wolfke concluded:
We see from this that with growing radiation density there occurs an association of light quanta into increasingly complex molecules, until finally—for very high radiation densities satisfying the Rayleigh-Jeans formula—the quanta agglomerate to form a continuous distribution in space. On the other hand, with decreasing radiation density the radiation continuum dissociates into simpler and simpler light molecules, until it ultimately dissolves into discrete light atoms!23 (Wolfke 1921, 378)
4.2.2 Louis de Broglie 1922
About one year later, without citing Wolfke’s publication, de Broglie published two short notes dealing with the particle properties of light and with Einstein’s expression for the energy fluctuations, the variance
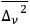 of black-body radiation (de Broglie 1922a; 1922b). He found on purely formal grounds that the expansion of Planck’s formula into
of black-body radiation (de Broglie 1922a; 1922b). He found on purely formal grounds that the expansion of Planck’s formula into
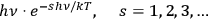 24 does not contradict Einstein’s fluctuation formula (Einstein 1909):
24 does not contradict Einstein’s fluctuation formula (Einstein 1909):
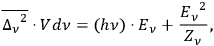
|
4.11 |
with
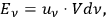
|
4.12 |
the time average of the energy at frequency
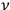 in a volume
in a volume
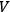 . According to Peter Debye (1884–1966):
. According to Peter Debye (1884–1966):
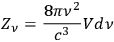
|
4.13 |
denotes the number of elementary states25 within a frequency interval,
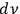 , for a black body of volume
, for a black body of volume
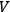 (Debye 1910).
(Debye 1910).
This is important historically because the two parts in Einstein’s fluctuation equation at that time were often literally connected to the particle
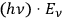 and wave aspect
and wave aspect
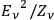 of light. In his results, de Broglie intuitively saw the physical picture of “coherent photons” (mono, duo, triple correlated photons) in the expansion of Planck’s formula, see eqs. (4.6), (4.7).26 Therefore, he was convinced that “if the theory of light-quanta ever succeeds in interpreting interference, it will require such agglomeration of quanta” (Darrigol 1991, 260).
of light. In his results, de Broglie intuitively saw the physical picture of “coherent photons” (mono, duo, triple correlated photons) in the expansion of Planck’s formula, see eqs. (4.6), (4.7).26 Therefore, he was convinced that “if the theory of light-quanta ever succeeds in interpreting interference, it will require such agglomeration of quanta” (Darrigol 1991, 260).
4.3 Dynamical Treatments of Light Multiples
4.3.1 Bothe 1923
Citing Wolfke’s 1921 publication only in passing, Bothe,27 Planck’s former student, submitted a manuscript entitled “Die räumliche Energieverteilung der Hohlraumstrahlung” to Zeitschrift für Physik in 1923 (Bothe 1923).28 At the time, Bothe worked at the Physikalisch Technische Reichsanstalt (PTR) in Berlin-Charlottenburg. Aside from his experimental work (Fick and Kant 2009), from mid-1923 to the end of 1926, he published a few theoretical papers, all of which dealt with the “light quantum problem.” In the acknowledgments and footnotes, more often than not, he thanked von Laue, who was a full professor at the Berlin University, a member of the Königlich Preußische Akademie der Wissenschaften (Prussian Academy of Sciences) and deputy director of the Kaiser Wilhelm Institut für Physik during that time (Hoffmann 2010, and references therein). In addition, Einstein was very influential. Einstein was also a member of the Prussian Academy. Beginning in 1914, he lived and worked in Berlin, and in 1916, he became a member of the Kuratorium (board of trustees) of the PTR. Since the light quantum problem was a primary concern of Bothe’s, he certainly kept in touch with Einstein.29 In his Nobel lecture, Bothe recalls this period: “During this time I had the singular good fortune of being able to discuss the [wave particle] problem constantly with Einstein” (Bothe 1964, 274).

Fig. 4.2: Walther Bothe. Courtesy of the Archives of the Max Planck Society, Berlin.
Beginning with Einstein’s formulation of emission and absorption processes (Einstein 1917), in his paper, Bothe studied how a two-level object (for example, an atom) achieves thermal equilibrium in a black-body radiation field. He characterized the atom by states
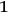 and
and
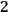 with energies
with energies
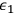 and
and
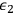 (
(
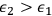 ) and occupation numbers
) and occupation numbers
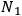 and
and
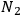 . According to Einstein, the atoms can undergo two types of emission processes by emitting a light quantum of energy
. According to Einstein, the atoms can undergo two types of emission processes by emitting a light quantum of energy
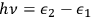 : a spontaneous one proportional to
: a spontaneous one proportional to
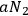 and an induced one proportional to
and an induced one proportional to
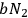 . The absorption of a light quantum with energy
. The absorption of a light quantum with energy
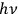 , inducing transitions from state
, inducing transitions from state
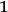 to state
to state
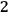 is then proportional to
is then proportional to
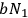 .30
The constants
.30
The constants
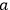 and
and
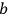 are characteristic for the transitions involved.
are characteristic for the transitions involved.
To introduce the concept of a “quantum multiple” for a fixed frequency
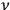 , Bothe reminds the reader that according to Einstein (1917), induced emission and absorption are, spatially, perfectly correlated processes. Moreover for stimulated emission, the inducing and stimulated quanta are perfectly correlated. They possess identical directions and energies (phases, polarizations).31 He noticed later that:
, Bothe reminds the reader that according to Einstein (1917), induced emission and absorption are, spatially, perfectly correlated processes. Moreover for stimulated emission, the inducing and stimulated quanta are perfectly correlated. They possess identical directions and energies (phases, polarizations).31 He noticed later that:
Both [quanta] are coupled seemingly; only seemingly, since in truth no forces exist between both, the dissociation energy […] is zero. If one of both quanta is absorbed, the fate of the other is not influenced at all; this is a consequence of the assumption that the probability of an induced process is simply proportional to the spatial density of the quanta. We shall therefore better speak about quantum pairs. If the inducing quantum already belongs to a pair, a triple will emerge, and so on.32 (Bothe 1923, 147)
It is clear that Bothe’s quantum multiples have only formally common aspects to Wolfke’s and de Broglie’s light molecules. Whereas both interpreted them more or less as real particles, Bothe in particular had the correlation aspect in mind. In our present understanding, we would instead call them “quasiparticles.”
Denoting the number density per frequency interval
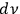 of single quanta, pairs, triples, …
of single quanta, pairs, triples, …
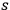 -fold multiples, of light quanta by
-fold multiples, of light quanta by
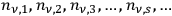 , Bothe first studied the thermal equilibrium conditions.33 Within a time interval
, Bothe first studied the thermal equilibrium conditions.33 Within a time interval
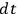 , single light quanta are produced with a probability of
, single light quanta are produced with a probability of
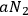 by spontaneous emission, and with a probability of
by spontaneous emission, and with a probability of
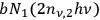 by absorption from a quantum pair, since
by absorption from a quantum pair, since
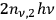 is the fraction of the total radiation density
is the fraction of the total radiation density
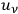 , which belongs to quantum pairs. These are the two source terms. On the other hand, single quanta disappear with a probability
, which belongs to quantum pairs. These are the two source terms. On the other hand, single quanta disappear with a probability
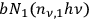 through an absorption process, and with a probability of
through an absorption process, and with a probability of
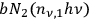 through conversion into a quantum pair in a stimulated emission process. These are the two drain terms. Since in thermal equilibrium the number of single quanta should be stationary, one obtains as a condition:
through conversion into a quantum pair in a stimulated emission process. These are the two drain terms. Since in thermal equilibrium the number of single quanta should be stationary, one obtains as a condition:
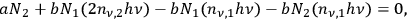
|
4.14 |
which couples singlets and doublets of quanta with the spontaneous decay (zero quantum).
The next higher-order rate equation, coupling singlets, doublets, and triplets with each other
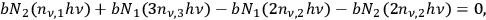
|
4.15 |
consists again of two source and two drain terms. The previous source term converting a doublet into a singlet now becomes a drain term for doublets, and the previous drain term for singlets now becomes a source term for doublets. This is the general structure of all higher-order rate equations. Two of the contributions always change sign in the next order equation.
Therefore, summing up these equations to the order of
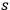 , most of the terms cancel each other out. One obtains a rate equation, which couples an
, most of the terms cancel each other out. One obtains a rate equation, which couples an
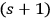 - and an
- and an
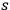 -fold quantum state with a single-quantum state and the term for the spontaneous decay:
-fold quantum state with a single-quantum state and the term for the spontaneous decay:
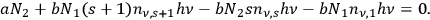
|
4.16 |
Only the spontaneous decay process,
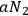 , cannot depend on the radiation densities for the various multiple quantum states. Since the total number of light quanta
, cannot depend on the radiation densities for the various multiple quantum states. Since the total number of light quanta
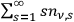 has to be finite, the number densities
has to be finite, the number densities
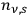 have to approach zero with increasing
have to approach zero with increasing
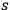 , yielding finally:
, yielding finally:
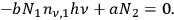
|
4.17 |
According to Boltzmann’s law, the occupation numbers
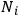
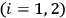 of the atomic states can be expressed as function of temperature34
of the atomic states can be expressed as function of temperature34
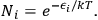
|
4.18 |
Following Einstein (1917), the ratio
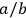 is then given by
is then given by
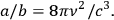
|
4.19 |
Bringing everything together,35 one obtains for the
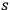 th multiple:
th multiple:

|
4.20 |
These number densities are formally identical to the ones obtained by Ishiwara and Wolfke through the expansion of Planck’s formula36 (Ishiwara 1912; Wolfke 1921). Therefore, summing up all the terms has to yield Planck’s formula again. However, as pointed out above, Bothe’s light multiples are correlated light quanta (quasiparticles), whereas Wolfke interpreted them as real objects.
Citing Lorentz (1916, 59), Bothe began the introduction to the publication with the remark that the energy variation (variance) of a black body holds the key to understanding radiation theory. Therefore, unlike Wolfke (1921), it was essential for him to address this topic as well. To do so, he extended Einstein’s analogy between an ideal gas and the light quantum gas consisting of independent constituents to the
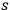 -fold multiples. Consequently, he assumed that the average number of
-fold multiples. Consequently, he assumed that the average number of
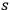 -fold multiples
-fold multiples
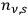 fluctuates in time in a Gaussian way as
fluctuates in time in a Gaussian way as
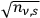 . Thus, the mean energy fluctuation squared of an
. Thus, the mean energy fluctuation squared of an
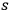 -fold multiple (energy
-fold multiple (energy
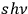 ) is
) is
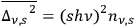 . Summing over all
. Summing over all
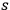 and using eq. (4.19), one obtains as variance
and using eq. (4.19), one obtains as variance
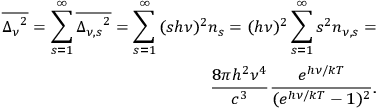
|
4.21 |
Finally, by replacing the temperature
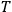 with
with
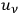 , the energy density per frequency interval, Planck’s formula, see eq. (4.1), one indeed obtains Einstein’s fluctuation formula (Einstein 1917)37:
, the energy density per frequency interval, Planck’s formula, see eq. (4.1), one indeed obtains Einstein’s fluctuation formula (Einstein 1917)37:
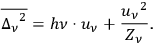
|
4.22 |
Bothe demonstrated at that time that the concept of light multiples allows a correct reproduction of Einstein’s fluctuation formula, in contrast to both classical theory and to simple light-quantum concepts. Even a wave concept was unnecessary to obtain the correct radiation (Planck) and fluctuation (Einstein) formulas, as long as spontaneous emission as well as phase-correlated induced emission and absorption are properly taken into account.
Nevertheless, there was at least one point that was not understood: why are there no
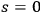 contributions in the expansion of Planck’s formula, see eq. (4.6), or in other words, why must the spontaneous decay be treated separately? This hampered an interpretation of the light quantum multiples in physical terms. We now address this question.
contributions in the expansion of Planck’s formula, see eq. (4.6), or in other words, why must the spontaneous decay be treated separately? This hampered an interpretation of the light quantum multiples in physical terms. We now address this question.
4.3.2 Bothe 1925a
Bothe resumed this topic a few years later in an as-yet unpublished manuscript entitled “Zur Struktur der Strahlung.”38 The manuscript is undated, but he worked on this until at least February 1925 when Planck, in a meeting of the Prussian Academy of Sciences, presented a paper “Zur Frage der Quantelung einatomiger Gase” (Planck 1925), which Bothe duly cited. Bose’s seminal paper had been published in the December 1924 issue of Zeitschrift für Physik (Bose 1924), just a couple of months earlier.
The main aim of the unpublished work was to find a bridge between the quantum picture and the wave picture of radiation. Bothe began the text with the following sentences:39
Einstein’s derivation of the radiation formula [variance of energy in a black body] (Einstein 1917) stands out due to its outstanding clarity. If one attempts to develop it further […], one obtains the strange picture that the light quanta within the stationary radiation field are in general not independent of each other, but rather bunched. Only by accounting for the bunching of the light quanta does one arrive at the correct expression for the energy fluctuations of the radiation field (Bothe 1923; Wolfke 1921). Unfortunately until now, no one has succeeded in building a bridge from this point to the classical wave theory, e. g., in specifying the number of degrees of freedom within a radiation volume, or even in interpreting the interferences.40,41

Fig. 4.3: Bothe manuscript, (n.d., ca. 1925). “Zur Struktur der Strahlung.” AMPG, III/6/105.4.
As we will see below, this drawback is closely connected to the missing
 term in the expansion of Planck’s formula in terms of Wienian-type
term in the expansion of Planck’s formula in terms of Wienian-type
 -fold light multiple energy distributions, see eqs. (4.6), (4.7), (4.20).
-fold light multiple energy distributions, see eqs. (4.6), (4.7), (4.20).
Bothe’s main idea was to use a heuristic argument to put the spontaneous and induced emission on equal footing. With a black-body radiation field consisting of
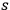 -fold light multiples according to sec. (4.2) in mind, he started his considerations again by questioning if and how thermal equilibrium is reached for his favored model system, the interaction of black-body radiation with two-level objects (atoms, molecules). He examined two processes:
-fold light multiples according to sec. (4.2) in mind, he started his considerations again by questioning if and how thermal equilibrium is reached for his favored model system, the interaction of black-body radiation with two-level objects (atoms, molecules). He examined two processes:
1The object is excited through interaction with an
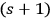 -fold multiple from the energetically lower state with energy
-fold multiple from the energetically lower state with energy
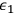 into the energetically higher state with energy
into the energetically higher state with energy
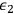 , whereby the
, whereby the
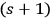 -fold light multiple of frequency
-fold light multiple of frequency
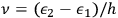 is transformed into an
is transformed into an
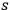 -fold light multiple of the same frequency
-fold light multiple of the same frequency
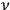 . Using additional Boltzmann statistics for the population of the states 1 and 2, see eq. (4.18), the incidence of such a process is, as before, proportional to
. Using additional Boltzmann statistics for the population of the states 1 and 2, see eq. (4.18), the incidence of such a process is, as before, proportional to
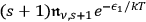 , since
, since
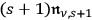 is the fraction of the total radiation density
is the fraction of the total radiation density
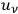 , which belongs to
, which belongs to
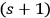 -fold multiples.42
-fold multiples.42
2The reverse process, the de-excitation of an excited molecule through interaction with an
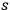 -fold light multiple, transforms it into an
-fold light multiple, transforms it into an
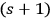 -fold one. To avoid a special role of the spontaneous transitions with respect to the induced ones, see section (4.3.1), Bothe now assumed on heuristic grounds that these transitions are proportional to
-fold one. To avoid a special role of the spontaneous transitions with respect to the induced ones, see section (4.3.1), Bothe now assumed on heuristic grounds that these transitions are proportional to
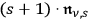 instead of
instead of
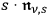 , surmising correctly, as early as 1925, a small part of modern field theory.43 The incidence of these processes is then proportional to
, surmising correctly, as early as 1925, a small part of modern field theory.43 The incidence of these processes is then proportional to
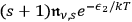 . Bothe himself commented on his ansatz very cautiously:
. Bothe himself commented on his ansatz very cautiously:
The addendin the bracket replaces to some extent the spontaneous transitions, since it allows now also for emission processes which start from a zero quantum multiplet.44
45
One benefit of this is that zero-fold multiples are formally allowed and would today be termed a “physical vacuum.” Thanks to Paul Dirac’s seminal work (Dirac 1927, 251/261, eq. 10), the factor
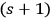 in front of terms describing the creation of light quanta (and of Bosons in general) is absolutely necessary to guarantee a symmetric wave function.46
in front of terms describing the creation of light quanta (and of Bosons in general) is absolutely necessary to guarantee a symmetric wave function.46
To achieve thermal equilibrium, both rates have to be equal, yielding
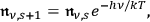
|
4.23 |
for all
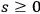 , from which
, from which
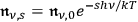
|
4.24 |
immediately follows.
Before we report on the consequences of Bothe’s ansatz, we anticipate a small detail of Bothe’s 1927 publication (Bothe 1927b) discussed at the end of section (4.3.3). This detail concerns the ratio
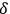 between the total rate of induced and spontaneous transitions in a black body. Drawing from Bothe’s less precise interpretation of the two parts in the factor
between the total rate of induced and spontaneous transitions in a black body. Drawing from Bothe’s less precise interpretation of the two parts in the factor
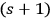 (see quotation above), he obtained
(see quotation above), he obtained
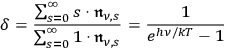
|
4.25 |
by means of eq. (4.24) for this ratio.
More recently,
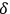 is called “degeneracy parameter.”47 It approaches “
is called “degeneracy parameter.”47 It approaches “
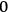 ” (no induced transitions) for the extreme Wien limit (
” (no induced transitions) for the extreme Wien limit (
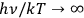 ) and “
) and “
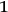 ” for the extreme Raleigh-Jeans limit (
” for the extreme Raleigh-Jeans limit (
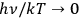 ).
).
In contrast to Wolfke’s (1921), de Broglie’s (1922b) and his own previous considerations (Bothe 1923), Bothe used his heuristic trick and found a possibility to also formally treat
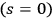 -multiples. Furthermore, using the last eq. (4.25), he gained an advanced interpretation of the total number density
-multiples. Furthermore, using the last eq. (4.25), he gained an advanced interpretation of the total number density
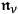 of light multiples, per frequency interval
of light multiples, per frequency interval
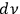 , including the zero-quantum ones. To reach this point, he identified
, including the zero-quantum ones. To reach this point, he identified
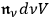 , the total number of light multiples per frequency interval
, the total number of light multiples per frequency interval
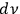 and volume
and volume
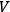 with the number of degrees of freedom of a black body
with the number of degrees of freedom of a black body
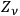 , see eq. (4.13):48
, see eq. (4.13):48
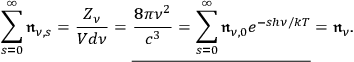
|
4.26 |
Performing the sum within the underlined part of the equation yields:
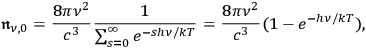
|
4.27 |
and thus
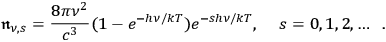
|
4.28 |
This equation can be rewritten as
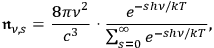
|
4.29 |
a required expression if the
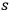 -fold light multiples in a black body are distributed thermodynamically according to Boltzmann’s law.49 Thus the
-fold light multiples in a black body are distributed thermodynamically according to Boltzmann’s law.49 Thus the
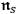 can now be interpreted thermodynamically as occupation number densities for the
can now be interpreted thermodynamically as occupation number densities for the
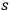 -fold multiples in a black body. Bothe was probably aware of this since he commented on his result as follows:
-fold multiples in a black body. Bothe was probably aware of this since he commented on his result as follows:
This is the new distribution law of the quantum multiples. From it one can easily derive the total radiation energyat frequency
[…], that is Planck’s formula:50
51
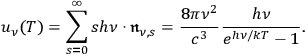
|
4.30 |
After having obtained this result, Bothe reminds the reader that, following Debye (1910), the number of degrees of freedom of a black-body radiator at frequency
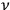 is nothing but the number of eigenmodes of the black body at that frequency
is nothing but the number of eigenmodes of the black body at that frequency
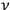 . Each of these eigenmodes can be replaced by a Planck oscillator of frequency
. Each of these eigenmodes can be replaced by a Planck oscillator of frequency
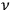 , and the number of eigenmodes with energy
, and the number of eigenmodes with energy
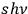 can be identified according to the quantum rules with
can be identified according to the quantum rules with
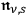 . Indeed, eq. (4.28) is identical to the statistical distribution law of the energies of
. Indeed, eq. (4.28) is identical to the statistical distribution law of the energies of
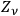 Planck oscillators. He ends with the remark:
Planck oscillators. He ends with the remark:
After this, we can interpret each quantum multiple in black-body radiation as the energy of an eigenmode of the black body.5253
In 1912, Ishiwara already had a similar interpretation in mind (Ishiwara 1912), starting from the power expansion of Planck’s formula, see eq. (4.6), and relying on Debye’s (1910) interpretation of phase space quantization. However, he did not get very far, since at that time in the expansion of Planck’s formula
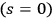 -terms were only previously discussed by Einstein at the 1911 Solvay Conference (Einstein 1913).54
-terms were only previously discussed by Einstein at the 1911 Solvay Conference (Einstein 1913).54
Bothe finally returns to the question of whether the correct expression of the energy fluctuations in a black body follows from the distribution law in eq. (4.28). He did not doubt this since the distribution law in eq. (4.28) correctly yields Planck’s formula. Nevertheless, he demonstrates this explicitly in a few lines.55
4.3.3 Bothe 1927
One can only speculate why Bothe did not publish the manuscript at the beginning of 1925. One reason was certainly his workload at the PTR. Hans Geiger (1882–1945), the director of the laboratory for radioactivity, had left the PTR around that time, and Bothe succeeded him. In Germany, the PTR was responsible for all official calibrations of radioactive samples.
The appearance of the Bose statistics and its implications might also have caused a delay in the publication of the manuscript. Moreover, apart from his daily duties, between 1926 and 1927, Bothe performed two crucial coincidence experiments which dealt with resonance fluorescence of X-rays (Bothe 1926) and later with Compton scattering in an X-ray interference field (Bothe 1927a). Both experiments were highly complex and very time consuming.56 It might therefore be that Bothe simply did not have enough time to finish the manuscript.
Using Compton scattering, Bothe found in the latter experiment that light quanta from an interference field still carry a momentum of
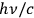 . Like Einstein,57 he considered his result to be extremely important, as we know from the handwritten notes for a talk he presented at the end of October 1926.58 At that time, he discussed standing waves of an interference field, which definitely represents a classical situation with a vanishing energy and momentum transport in total. Light quanta in an interference field, as well as in a directed (needle) beam, nevertheless possess a momentum of
. Like Einstein,57 he considered his result to be extremely important, as we know from the handwritten notes for a talk he presented at the end of October 1926.58 At that time, he discussed standing waves of an interference field, which definitely represents a classical situation with a vanishing energy and momentum transport in total. Light quanta in an interference field, as well as in a directed (needle) beam, nevertheless possess a momentum of
 .
.
Gathering the main ideas of his unpublished manuscript, Bothe reacted to this situation with a short publication, again reinterpreting the concept of light multiples (Bothe 1927b). Since a monochromatic unidirectional needle beam is a non-physical object, he used von Laue’s (1914) light bundles of a finite cross section and of a very small frequency and opening angle interval as “elementary cells,” in which the light quanta are embedded. He considered these bundles, together with the embedded quanta, as independent entities of the radiation statistics. Each bundle could contain an arbitrary amount of light quanta (including zero), whereby the number of elementary bundles per volume
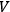 and frequency range
and frequency range
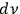 was identical to the number of degrees of freedom
was identical to the number of degrees of freedom
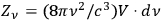 , see eq. (4.26). In this way, Bothe followed the new Bose statistics, which led to a sort of coupling between the light quanta, as had already been noted by a few others (Einstein 1924; Ehrenfest 1925; Landé 1925). With this interpretation in mind, Bothe demonstrated that not only the number of light quanta for a black body in thermal equilibrium is stationary but so is their grouping.
, see eq. (4.26). In this way, Bothe followed the new Bose statistics, which led to a sort of coupling between the light quanta, as had already been noted by a few others (Einstein 1924; Ehrenfest 1925; Landé 1925). With this interpretation in mind, Bothe demonstrated that not only the number of light quanta for a black body in thermal equilibrium is stationary but so is their grouping.
As frequently emphasized, Bothe considered the understanding of Einstein’s fluctuation formula, see eq. (4.22), to be extremely important. He therefore concluded this publication with an alternative derivation which used the dual concept of light directly. Since its formal procedure is only of minor interest here, we outline the main idea and present the final result. Following Lorentz (1916), Bothe began with the remark that in an elementary bundle, the (classical) wave energy
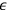 fluctuates around its average
fluctuates around its average
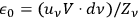 with a variance (root mean square fluctuation)
with a variance (root mean square fluctuation)
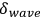 equal to the average wave energy itself:59
equal to the average wave energy itself:59
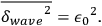
|
4.31 |
In classical physics, this would be the total fluctuation of the averaged energy. However, if one assumes that the wave energy is distributed discontinuously over “light particles” (quanta), the number of light particles
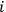 itself fluctuates around its average value
itself fluctuates around its average value
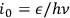 with a variance of
with a variance of
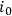 if a Poisson distribution is assumed. The variance of the energy due to the fluctuation of the number of light particles is therefore
if a Poisson distribution is assumed. The variance of the energy due to the fluctuation of the number of light particles is therefore
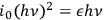 . Furthermore, averaging over the energy
. Furthermore, averaging over the energy
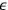 itself, one obtains for the variance (root mean square fluctuation) of this contribution:
itself, one obtains for the variance (root mean square fluctuation) of this contribution:
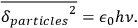
|
4.32 |
The tricky aspect of the problem now is that both variances are coupled, since the fluctuation of the number of particles depends on the fluctuation of the (wave) energy. Nevertheless, in an appendix Bothe proved that these two variances simply add to each other:
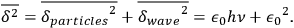
|
4.33 |
Multiplying the variance
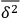 with the number of independent elementary bundles per volume and frequency interval
with the number of independent elementary bundles per volume and frequency interval
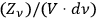 , one obtains the known result, see eq. (4.22), which we repeat here for easy comparison:
, one obtains the known result, see eq. (4.22), which we repeat here for easy comparison:
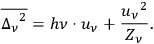
|
4.34 |
As Bothe pointed out, this equation followed from a systematic treatment of the dualistic nature of light and does not follow from a plain addition of the fluctuations of the separate results that treat light first as a wave and then as a light particle. As we now know, Poissonian distributed particle numbers, for example light quanta in a black body, always end up in energy fluctuations “expressible as the sum of contributions from the fluctuations of classical particles and the contributions of classical wave fields” (Mandel and Wolf 1965, 271, eq. 6.19 and its discussion; Born 1949, 79–82).60
With this manuscript, Bothe completed his research on the nature of light quanta for the rest of his scientific career. He never returned to the concept of light multiples. Nevertheless, one aspect of Bothe’s manuscript stood the test of time and is still cited today, his discussion of the degeneracy parameter
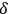 , see eq. (4.25). Due to its definition, it may also be considered the average number of light quanta that are in the same quantum state. There is a third interpretation of
, see eq. (4.25). Due to its definition, it may also be considered the average number of light quanta that are in the same quantum state. There is a third interpretation of
 as a ratio between the multi-light quantum states (
as a ratio between the multi-light quantum states (
 ) and the one-light quantum states (
) and the one-light quantum states (
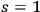 ) of thermal radiation
) of thermal radiation
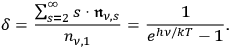
|
4.35 |
Multi-light quantum states (
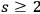 ) are generated by various sequences of induced transitions. According to Einstein (1917), light quanta from induced transitions are perfectly correlated in direction, energy, phase and polarization. Due to the latter interpretation of
) are generated by various sequences of induced transitions. According to Einstein (1917), light quanta from induced transitions are perfectly correlated in direction, energy, phase and polarization. Due to the latter interpretation of
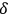 , it is therefore comprehensible that correlation functions in space are proportional to the degeneracy parameter
, it is therefore comprehensible that correlation functions in space are proportional to the degeneracy parameter
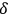 .61
.61
In their seminal experiments during 1957–1958, Robert Hanbury Brown and Richard Twiss were the first to provide experimental evidence of space correlations between the outputs of two photoelectric detectors illuminated by partially-correlated light waves of a mercury lamp in a Michelson configuration. In such experiments, the magnitude of the correlation coefficient is proportional to
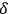 .62
.62
We end this section with the remark that in 1958 Hanbury Brown and Twiss determined the correlation of light of the star Sirius A, a black body of about 10,000K surface temperature for the first time (Mandel and Wolf 1995, Chap. 9.10 and references therein). The observation of correlations is an experimental proof that the concept of light molecules à la Ishiwara (1912), Wolfke and the early Bothe, see secs. (4.2.1) and (4.3.1), is useless. It has long been known that the expansion of Planck’s formula into a sum of the Wienian terms
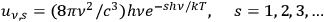 (eqs. (4.6), (4.7)) can be interpreted in terms of thermodynamically-independent objects (light molecules) with energy
(eqs. (4.6), (4.7)) can be interpreted in terms of thermodynamically-independent objects (light molecules) with energy
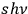 , since their partial entropies
, since their partial entropies
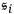 add up to the total entropy
add up to the total entropy
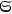 of a black body (sec. (4.2.1)). If this holds, then correlations of light from such an object should not exist; the light should be completely incoherent and thus unable to produce any interference effects at all (Laue 1906).63
of a black body (sec. (4.2.1)). If this holds, then correlations of light from such an object should not exist; the light should be completely incoherent and thus unable to produce any interference effects at all (Laue 1906).63
 64
64
4.4 Obituary
In 1930, Indian theorists R. J. Majumdar and D. S. Kothari published a thorough derivation of the ratio of Einstein’s
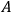 and
and
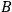 coefficients, following the ideas of Bose’s brief first 1924 manuscript (Bose 1924). In passing, they also mention Bothe’s considerations to obtain this ratio through the requirement of achieving thermal equilibrium in a black body (Bothe 1923). Here, we will not deal with their work, but instead with their remark that “Bothe created the fairly new concept of light molecules and arrived thus at Planck’s formula” (Majumdar and Kothari 1930).65 It was probably common knowledge, at least in India, that the Indian theorist Kulesh Ch. Kar also shared the same opinion (Kar 1927). Wolfke, now a professor at the Technical University in Warsaw, reacted angrily in a short note (Wolfke 1930) listing all the authors who had used the concept of “light atoms” or “light molecules”: Ioffe (1911), Wolfke (1921), de Broglie (1922b), Bateman (1923) and Bothe (1923).
coefficients, following the ideas of Bose’s brief first 1924 manuscript (Bose 1924). In passing, they also mention Bothe’s considerations to obtain this ratio through the requirement of achieving thermal equilibrium in a black body (Bothe 1923). Here, we will not deal with their work, but instead with their remark that “Bothe created the fairly new concept of light molecules and arrived thus at Planck’s formula” (Majumdar and Kothari 1930).65 It was probably common knowledge, at least in India, that the Indian theorist Kulesh Ch. Kar also shared the same opinion (Kar 1927). Wolfke, now a professor at the Technical University in Warsaw, reacted angrily in a short note (Wolfke 1930) listing all the authors who had used the concept of “light atoms” or “light molecules”: Ioffe (1911), Wolfke (1921), de Broglie (1922b), Bateman (1923) and Bothe (1923).
Around this time, Wolfke still maintained his relations with Einstein. The Einstein Archive Online lists a total of nine letters exchanged between Wolfke and Einstein from 1925 to 1931. Wolfke’s letter dated 13 December 1925 refers to a recent meeting with Einstein in Berlin.66 Some of the other letters deal with Wolfke’s ideas to experimentally find a signal pointing to the existence of (static) light molecules. Moreover, at Wolfke’s request, Einstein presented an investigation entitled “Über die statistischen Eigenschaften der Strahlung” (Einstein 1930) at a meeting of the Prussian Academy of Sciences in which Einstein arrived at a fluctuation formula with a factor two in front of the “wave part”, see eq. (4.22). The corresponding manuscript never appeared.
In two letters dated 27 and 29 December 1930,67 Wolfke tried to corroborate Einstein’s result with his own calculations. In his second letter, he was almost headed in the right direction. He started with Bose’s expression for the occupation probability of a phase space cell with
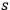 light quanta (Bose 1924) and identified this probability with the number density
light quanta (Bose 1924) and identified this probability with the number density
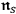 of
of
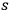 -fold light multiples with energy
-fold light multiples with energy
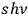 .68 By this means, he arrived at Bothe’s expression for
.68 By this means, he arrived at Bothe’s expression for
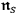 , see eq. (4.28), however, with one essential difference. According to his interpretation of the
, see eq. (4.28), however, with one essential difference. According to his interpretation of the
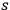 -fold multiples in terms of static light molecules, he assumed that
-fold multiples in terms of static light molecules, he assumed that
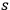 runs only from
runs only from
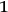 to
to
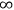 , instead of from
, instead of from
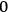 to
to
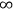 as Bothe interpreted. Calculating the total energy density by
as Bothe interpreted. Calculating the total energy density by
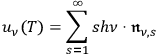
|
4.36 |
and its averaged energy fluctuation density squared
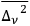 through (Bothe 1923, eq. 1)
through (Bothe 1923, eq. 1)
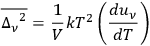
|
4.37 |
he obtained the correct result for the total energy density, but a factor of two in front of the wave part of the averaged energy fluctuation density squared, see eq. (4.22), as had Einstein. One can straightforwardly identify this odd result with the missing
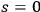 term and thus with the interpretation of the
term and thus with the interpretation of the
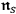 . Wolfke drew the proper conclusion “[…] that on the basis of the Bose – Einstein statistics it is not permissible to interpret the radiation field as consisting of multiple quanta.”69
. Wolfke drew the proper conclusion “[…] that on the basis of the Bose – Einstein statistics it is not permissible to interpret the radiation field as consisting of multiple quanta.”69
Einstein probably made the same mistake, since we know from a brief remark at the bottom of Wolfke’s 29 December 1930 letter that he calculated the energy fluctuations assuming a mixture of locally independent multiple quanta.70 After returning to Berlin, Einstein responded in detail in a letter dated 10 April 193171 by saying “At first, I was very impressed by your argument. But then I found a problem.”72 Einstein then showed explicitly that the concept of static light molecules violates Boltzmann’s law.73 No reply from Wolfke is known.
The story of “light molecules” related here ends finally in 1946. Wolfke survived the German occupation of Poland in Warsaw. Here he taught, partly at a lower level, at the Polytechnic University where he was a professor. After the war, he was eager to resume his contacts with the West, in particular to Sweden, Switzerland and, if possible, to the United States. From Stockholm, he sent a manuscript entitled “Über Multiphotone”74 to Einstein in Princeton asking him for critical remarks. Wolfke, still drawing from his 1921 publication on black-body radiation (Wolfke 1921), showed that the number of phase cells that contain
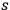 quanta of energy
quanta of energy
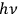 equals the number density of multiphotons
equals the number density of multiphotons
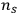 with energy
with energy
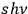 , see eq. (4.9) according to Bose-Einstein statistics.75 Subsequently, he discussed potentially feasible experiments using the light emitted by black bodies of extremely high temperatures, such as fixed stars, to enhance the ratio of
, see eq. (4.9) according to Bose-Einstein statistics.75 Subsequently, he discussed potentially feasible experiments using the light emitted by black bodies of extremely high temperatures, such as fixed stars, to enhance the ratio of
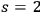 to
to
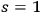 multiphotons, see eq. (4.10).
multiphotons, see eq. (4.10).

Fig. 4.4: Letter from Wolfke to Einstein dated 10 July 1946, APAN, III–71/IV.23,5.
In September 1946, Wolfke presented his ideas at a meeting of the Schweizerische Naturforschende Gesellschaft in Zurich.76 Previously, on 18 January, de Broglie77 had already presented a French version of the manuscript78 at the meeting of the Académie des Sciences, Paris, which was published in Comptes Rendus (Wolfke 1946c).
Einstein answered Wolfke’s letter one week later on 17 July 1946.79 In this correspondence, Einstein argued against the existence of “light molecules” in discussing the passage of light molecules through a semi-reflecting plate. In doing so, he elaborated at length his argument from his 1909 letter to Lorentz80 that “a light ray splits, but a light quantum cannot split without a change in frequency.” Obviously Einstein had forgotten his much more convincing argument from his 1931 letter to Wolfke that the existence of static light molecules is not in accordance with Boltzmann’s law.
Wolfke replied to Einstein’s letter on 17 August 1946 without really responding to Einstein’s critical remark. Wolfke passed away in Zurich on 4 May 1947 after suffering a heart attack. After Bothe’s withdrawal in 1927, this incident finally brought to an end the discussion on the concept of “light molecules” as a tool for dealing with the correlations in a light quantum gas.
Appendix
Frequency Continuum and Light Molecules
Wolfgang Pauli 1923
In 1923, Wolfgang Pauli (1900–1958) tried to understand whether, and if so how, free electrons with a Maxwellian velocity distribution can achieve thermal equilibrium in a black-body radiation field (Pauli 1923). He assumed that the (relativistically-treated) Compton effect is the mechanism which drives the system into equilibrium, since it allows for a change of the energy and momentum of both light quantum and electron. Of course, the relativistically-formulated conservation laws of energy and momentum had to be fulfilled as well. He identified statistical equilibrium through the condition that each elementary process occurs as often as the time-reversed process. To substantiate this requirement, Pauli devoted quite some effort to the formal description of what a time-reversed process means relativistically.
Apart from such dynamical variables as the momenta of electron and photon, and apart from the solid angle, the rates depend then on a “rate function” (Häufigkeitsfunktion)
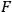 which ought to depend explicitly on
which ought to depend explicitly on
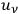 , the spectral density of an arbitrary radiation field at frequency
, the spectral density of an arbitrary radiation field at frequency
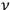 with which the electrons are interacting. At first Pauli tested the plausible ansatz
with which the electrons are interacting. At first Pauli tested the plausible ansatz
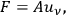
|
4.38 |
whereby the function
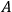 ought to depend on the kinematical variables of electron and the light quanta, such as the momenta and energies, but be independent of temperature
ought to depend on the kinematical variables of electron and the light quanta, such as the momenta and energies, but be independent of temperature
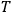 . Pauli found that this ansatz leads unambiguously to Wien’s radiation law.
. Pauli found that this ansatz leads unambiguously to Wien’s radiation law.
Guided by a qualitative analysis of this apparently limited ansatz, he analyzed the consequences of the, at first glance, rather strange ansatz
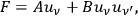
|
4.39 |
in which
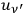 denotes the radiation density at the frequency of the Compton-scattered light quantum. Pauli himself commented on this as follows: “At first glance this postulation seems odd, since an interaction of radiation bundles is assumed here, possibly with widely different frequencies”81 (Pauli 1923, 284). This ansatz causes the Compton scattering process
denotes the radiation density at the frequency of the Compton-scattered light quantum. Pauli himself commented on this as follows: “At first glance this postulation seems odd, since an interaction of radiation bundles is assumed here, possibly with widely different frequencies”81 (Pauli 1923, 284). This ansatz causes the Compton scattering process
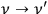 to occur more frequently if the frequencies
to occur more frequently if the frequencies
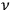 as well as
as well as
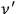 are present in the radiation field. And indeed, this leads to Planck’s radiation law for a black body.
are present in the radiation field. And indeed, this leads to Planck’s radiation law for a black body.
Einstein and Ehrenfest reacted immediately in the next issue of Zeitschrift für Physik (Einstein and Ehrenfest 1923). Obviously, they had had access to Pauli’s manuscript in advance and had submitted their manuscript prior to the appearance of Pauli’s. In subsequent steps, Einstein and Ehrenfest employed a transparent formalism which allowed equilibrium conditions to be described for absorption and emission of radiation, even when the matter part has continuous energy spectra, as in Compton scattering, for example, or for moving atoms or molecules. By defining what “time reversal” in the statistical average might mean, Einstein and Ehrenfest arrived at transition probabilities that were nonlinear in the energy density of the radiation field, in general, up to any order.82
Bothe 1924
Bothe also reacted to Pauli’s investigations with a formulation of the problem in terms of quantum multiples. He aimed at a proof in which the “B-processes” in Pauli’s sense, see eq. (4.39), are formally dispensable (Bothe 1924). We will not enter the formal details of his arguments since they were based on the light multiple concept without the
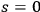 terms, which as we saw, is problematic, see secs. (4.2) and (4.3.1).
terms, which as we saw, is problematic, see secs. (4.2) and (4.3.1).
Bothe’s final argument was based on two recollections:
1Pauli (1923) showed that with the A-term alone, see eq. (4.38), the thermalization of a light-quantum gas in a black body through Compton scattering on a thermalized electron gas (Boltzmann distribution) will unambiguously lead to a Wienian energy distribution.
2Referring to Wolfke (1921), see sec. (4.2.1), de Broglie (1922a), see sec. (4.2.2), and to his own work (Bothe 1923), see sec. (4.3.1), he reminded the reader that Planck’s formula may be written as an infinite sum of Wienian terms, each describing an
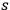 -fold light multiple:
-fold light multiple:
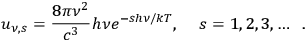
|
4.40 |
Thus it will suffice to deal with Compton scattering of
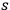 -fold quantum multiples as a whole, taking into account only A-processes, see eq. (4.38). Formally, such a process might be written as
-fold quantum multiples as a whole, taking into account only A-processes, see eq. (4.38). Formally, such a process might be written as
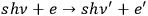 . The number of
. The number of
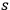 -fold multiples will be conserved and only their frequency will vary. One just has to formally replace in Pauli’s calculations (Pauli 1923, 281–282)
-fold multiples will be conserved and only their frequency will vary. One just has to formally replace in Pauli’s calculations (Pauli 1923, 281–282)
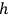 with
with
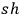 , which will result with Wienian terms in
, which will result with Wienian terms in
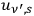 , the sum of which will yield Planck’s formula again and thus thermalized black-body radiation.
, the sum of which will yield Planck’s formula again and thus thermalized black-body radiation.
Bothe then added a more formal and detailed support of this brief argument. He finished the paper with the remark that in Pauli’s derivation, as well as in his own, the number of light quanta is conserved. Moreover, the achievement of thermal equilibrium is independent of the prefactor
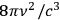 in Planck’s law.83
in Planck’s law.83
Bothe 1925b
In his unpublished manuscript,84 Bothe set about remedying this problem. He used the heuristic trick described in sec. (4.3.2). Still using the concept of
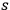 -fold light multiples, he again assumed that the rate of processes in which an
-fold light multiples, he again assumed that the rate of processes in which an
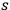 -fold light multiple loses a light quantum is proportional to its energy density
-fold light multiple loses a light quantum is proportional to its energy density
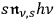 , but proportional to
, but proportional to
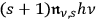 for those processes in which it gains one.85
for those processes in which it gains one.85
Apart from this assumption, he followed Pauli’s strategy (Pauli 1923) and discussed the following two elementary steps in the interaction of light quanta with Maxwellian-energy-distributed electrons: in an interaction of an electron (momentum
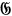 ) with an
) with an
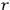 -fold light multiple
-fold light multiple
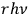 of frequency
of frequency
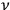 the latter loses one light quantum with momentum
the latter loses one light quantum with momentum
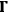 which is added with momentum
which is added with momentum
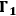 to a
to a
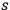 -fold light multiple
-fold light multiple
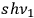 of frequency
of frequency
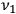 . The electron scatters under an angle
. The electron scatters under an angle
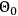 and thus takes care of the momentum and energy conservation (
and thus takes care of the momentum and energy conservation (
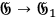 ).86 Applying once more the heuristic trick described in sec. (4.3.2), Bothe assumed that the rate of the process is proportional to the energy density
).86 Applying once more the heuristic trick described in sec. (4.3.2), Bothe assumed that the rate of the process is proportional to the energy density
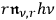 of the multiples which lose a light quantum, but proportional to
of the multiples which lose a light quantum, but proportional to
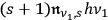 for those which gain one. Denoting for a Maxwellian velocity distribution at temperature T the number of electrons per unit volume within the momentum interval
for those which gain one. Denoting for a Maxwellian velocity distribution at temperature T the number of electrons per unit volume within the momentum interval
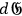 by
by
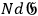 , the rate of these processes will be
, the rate of these processes will be
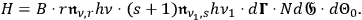
|
4.41 |
The strength
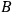 depends on all the relevant variables necessary to describe the process, except for the temperature
depends on all the relevant variables necessary to describe the process, except for the temperature
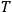 . The rate for the time reversed process can be parameterized accordingly
. The rate for the time reversed process can be parameterized accordingly
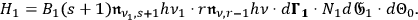
|
4.42 |
For the argument to be made, it is important only that
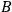 and
and
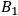 do not depend on temperature
do not depend on temperature
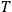 . To achieve thermal equilibrium it is sufficient that
. To achieve thermal equilibrium it is sufficient that
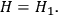
|
4.43 |
Pauli (1923, 281, eq. 25) deduced, from momentum and energy conservation for the electron-light quantum scattering, that the ratio
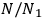 obeys the relation
obeys the relation
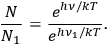
|
4.44 |
Now using the distribution for the number of multiples, see eq. (4.28)
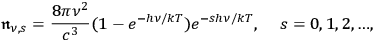
|
4.45 |
which we have already seen is in accordance with Boltzmann’s law, one finds rather easily that the temperature disappears under the condition
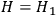 , see eq. (4.43). That means thermal equilibrium will be reached independently of the very form of the functions
, see eq. (4.43). That means thermal equilibrium will be reached independently of the very form of the functions
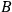 and
and
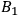 .
.
We conclude this section of the appendix with an interpretation of the result in terms of light bundles of finite cross section and of very small frequency and opening angle interval as “elementary cells,” in which the light quanta are embedded, see sec. (4.3.3). The process denoted by
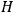 , see eq. (4.41), describes a scattering process in which, out of an elementary bundle with
, see eq. (4.41), describes a scattering process in which, out of an elementary bundle with
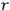 light quanta of frequency
light quanta of frequency
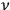 , one quantum is scattered into another bundle (called bundle
, one quantum is scattered into another bundle (called bundle
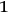 ) already hosting
) already hosting
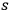 light quanta with frequency
light quanta with frequency
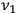 . The electron takes care of the energy and momentum conservation.
. The electron takes care of the energy and momentum conservation.
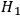 describes the time-reversed process. It is now important that also
describes the time-reversed process. It is now important that also
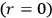 -terms contribute to
-terms contribute to
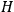 , which means that in the bundles of
, which means that in the bundles of
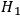 , light quanta may appear spontaneously. For example, in the time-reversed process denoted by
, light quanta may appear spontaneously. For example, in the time-reversed process denoted by
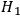 , a light quantum disappears completely for
, a light quantum disappears completely for
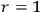 and is created spontaneously for
and is created spontaneously for
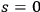 .
.
Abbreviations and Archives
| APAN | Archive of the Polish Academy of Sciences, Warsaw |
| AMPG | Archive of the Max Planck Society, Berlin |
| Einstein Archive Online | Albert Einstein Archives and the David and Fela Shapell Digitization Project at the Jewish National & University Library, the Hebrew University of Jerusalem, http://www.alberteinstein.info/database/ |
Acknowledgements
We thank the staff at the following institutions for their continuous help and support: Archive of the Max Planck Society and the library of the Fritz-Haber-Institut in Berlin, the Archive of the Polish Academy of Science in Warsaw, and the library of the Physics Department of the Philipps-Universität in Marburg. Additionally, we acknowledge the indispensable help of Dr. Tilman Sauer from the Einstein Papers Project in Pasadena (California, USA) and, last but not least, of our Polish colleagues Dr. Z. Lewandowski (Krakow), Prof. A. Kiejna (Wrocław), Prof. P. Zupranski (Warsaw) and Prof. W. Zych (Warsaw).
References
Abraham, Max (1905). Theorie der Elektrizität, Zweiter Band: Elektromagnetische Theorie der Strahlung. Leipzig: B. G. Teubner.
Afsenius, Sven-Åke (1975). Simple Approach to the Multiphoton States of a Thermal Radiation Field. American Journal of Physics 43: 882-884
Anonymous (1927). Report on talk by A. Einstein “Frage der Entstehung des Lichtes”. Zeitschrift für Angewandte Chemie 40: 546
- (1930). News and Views. Nature 126: 660
Bateman, Harry (1923). On the Theory of Light Quanta. Philosophical Magazine 46: 977-991
Bergia, Silvio, Carlo Ferrario, C. F. (1985). Side Paths in the History of Physics: The Idea of Light Molecule from Ishiwara to de Broglie. Rivista di storia della scienza 2: 71-97
Born, Max (1949). Natural Philosophy of Cause and Chance: The Waynflete Lectures 1948. Oxford: Oxford University Press.
Bose, Satyendra Nath (1924). Plancks Gesetz und Lichtquantenhypothese. Zeitschrift für Physik 26: 178-181
Bothe, Walther (1923). Die räumliche Energieverteilung der Hohlraumstrahlung. Zeitschrift für Physik 20: 145-152
- (1924). Über die Wechselwirkung zwischen Strahlung und freien Elektronen. Zeitschrift für Physik 23: 214-224
- (ca.1925). Zur Struktur der Strahlung. AMPG, III/6/105.4.
- (ca.1926). Lecture Notes. AMPG, III/6/105.3.
- (1926). Über die Kopplung zwischen elementaren Strahlungsvorgängen. Zeitschrift für Physik 37: 547-567
- (1927a). Lichtquanten und Interferenz. Zeitschrift für Physik 41: 332-344
- (1927b). Zur Statistik der Hohlraumstrahlung. Zeitschrift für Physik 41: 345-351
- (1964). The Coincidence Method. In: Nobel Lectures, Physics, 1942–1964 Amsterdam: Elsevier 271-276
Cassidy, David C. (2005). Einstein and the Quantum Hypothesis. Annalen der Physik 14: 15-22
Darrigol, Olivier (1988). Statistics and Combinatorics in Early Quantum Theory. Historical Studies in the Physical and Biological Sciences 19: 17-80
- (1991). Statistics and Combinatorics in Early Quantum Theory, II: Early Symptoma of Indistinguishability and Holism. Historical Studies in the Physical and Biological Sciences 21: 237-298
- (2009). A Simplified Genesis of Quantum Mechanics. Studies in History and Philosophy of Modern Physics 40: 151-166
de Broglie, Louis (1922a). Rayonnement noir et quanta de lumière. Journal de Physique et le Radium 3: 422-428
- (1922b). Sur les interférences et la théorie de quanta de lumière. Comptes Rendus de l'Académie des Sciences 175: 811-813
Debye, Peter (1910). Der Wahrscheinlichkeitsbegriff in der Theorie der Strahlung. Annalen der Physik 33: 1427-1434
- (1923). Zerstreuung von Röntgenstrahlen und Quantentheorie. Physikalische Zeitschrift 24: 161-166
Dirac, Paul A. M. (1927). The Quantum Theory of the Emission and Absorption of Radiation. Proceedings of the Royal Society A 114: 243-265
Duncan, Anthony, Michel Janssen (2008). Pascual Jordan's Resolution of the Conundrum of the Wave-Particle Duality of Light. Studies in History and Philosophy of Modern Physics 39(3): 634-666
Ehrenfest, Paul (1925). Energieschwankungen im Strahlungsfeld oder Kristallgitter bei Superposition quantisierter Eigenschwingungen. Zeitschrift für Physik 34: 362-373
Einstein, Albert (1905). Über einen die Erzeugung und Verwendung des Lichtes betreffenden heuristischen Gesichtspunkt. Annalen der Physik 17: 132-148
- (1909). Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung. Physikalische Zeitschrift 10: 817-825
- (1913). Solvay Conference 1911: Zum gegenwärtigen Stand des Problems der spezifischen Wärme. Abhandlungen der Deutschen Bunsen-Gesellschaft 7: 330-370
- (1916). Zur Quantentheorie der Strahlung. Mitteilungen der Physikalischen Gesellschaft Zürich 18: 47-62
- (1917). Zur Quantentheorie der Strahlung. Physikalische Zeitschrift 18: 121-128
- (1924). Quantentheorie des einatomigen idealen Gases. Sitzungsberichte der Preußischen Akademie der Wissenschaften zu Berlin
- (1930). Statistische Eigenschaften der Strahlung. Sitzungsberichte der Preußischen Akademie der Wissenschaften zu Berlin
Einstein, Albert, Paul Ehrenfest (1923). Zur Quantentheorie des Strahlungsgleichgewichtes. Zeitschrift für Physik 19: 301-306
Feynman, Richard P., Robert B. Leighton, R.B. L. (1965). The Feynman Lectures on Physics. Reading, MA: Addison-Wesely.
Fick, Dieter (in print). Bothe’s 1925 Heuristic Assumption in the Dawn of Quantum Field Theory. The European Physical Journal H
Fick, Dieter, Horst Kant (2009). Walther Bothe's Contributions to the Understanding of the Wave-Particle Duality of Light. Studies in History and Philosophy of Modern Physics (SHPMP) 40: 395-405
Frenkel, Viktor Ya. (1971). Yurij Aleksandrovich Krutkov. Soviet Physics Uspekhi 13(6): 816-824
Fürth, Reinhold (1928a). Schwankungserscheinungen nach der neuen Quantenstatistik. Zeitschrift für Physik 48: 323-339
- (1928b). Über Strahlungsschwankungen nach der Lichtquantenstatistik. Zeitschrift für Physik 50: 310-318
Hoffmann, Dieter (2010). Nicht nur ein Kopf, sondern auch ein Kerl! Zum Leben und Wirken Max von Laues (1879–1960). Physik Journal 9(5): 39-43
Ioffe, Abram F. (1911). Zur Theorie der Strahlungserscheinungen. Annalen der Physik 36: 534-552
- (1983). Vstrechi s fizikami (Meeting physicists). Leningrad: Izd. Nauka.
- (1985). O fizike i fizikach (On physics and physicists). Leningrad: Izd. Nauka.
Ishiwara, Jun (1912). Zur Theorie der Strahlungserscheinungen. Physikalische Zeitschrift 13: 1142-1151
Jordan, Pascual (1928). Das photochemische Gesetz und die molekulare Theorie der Strahlung. Physikalische Zeitschrift 7: 158-208
- (1929). Der gegenwärtige Stand der Quantenelektrodynamik. Physikalische Zeitschrift 30: 700-712
Kar, Kulesh Ch. (1927). Die Quantenstatistik. Physikalische Zeitschrift 28: 300-302
Kiejna, Adam (2002). Stanisław Loria and Mieczysław Wolfke in Wrocław—Bridging the German Past and the Polish Present. In: Proceedings of the 17th Max Born Symposium, Wrocław, Poland, 2002 Ed. by Jerzy Lukierski, Helmut Rechenberg. Wrocław: Wydawn. Uniwersytetu Wrocławskiego 49-69
Kirchner, Fritz (1930). Allgemeine Physik der Röntgenstrahlung. In: Handbuch der Experimentalphysik Ed. by Wilhelm Wien Freidrich Harms. Leipzig: Akademische Verlagsgesellschaft
Klein, Martin J., Anne J. Kox, A.J. K. (1993). The Collected Papers of Albert Einstein. Princeton, N.J.: Princeton University Press.
Kuhn, Thomas S. (1987). Black-Body Theory and the Quantum Discontinuity 1894–1912. Chicago: The University of Chicago Press.
Landé, Alfred (1925). Lichtquanten und Kohärenz. Zeitschrift für Physik 33: 571-578
Lanyi, Gabor E. (2003). Thermal Equilibrium Between Radiation and Matter. Foundations of Physics 33: 511-527
Laue, Max (1906). Zur Thermodynamik der Interferenzerscheinungen. Annalen der Physik 20: 365-378
- (1907a). Die Entropie von partiell kohärenten Strahlenbündeln. Annalen der Physik 23: 1-43
- (1907b). Die Entropie von partiell kohärenten Strahlenbündeln: Nachtrag. Annalen der Physik 23: 795-797
von Laue, Max (1914). Die Freiheitsgrade von Strahlenbündeln. Annalen der Physik 44: 1197-1212
Lewis, Gilbert N. (1926). The Conservation of Photons. Nature 118: 874-875
Lewis, Henry R. (1973). Einstein's Derivation of Planck's Radiation Law. American Journal of Physics 41: 38-44
Lorentz, Hendrik A. (1916). Les théories statistiques en thermodynamique. Leipzig: B. G. Teubner.
Majumdar, R. J., D. S. Kothari (1930). Statistische Deutung zur Einsteinschen Ableitung des Planckschen Gesetzes. Zeitschrift für Physik 60(3–4): 250-254
Mandel, Leonard, Emil Wolf (1965). Coherence Properties of Optical Fields. Review of Modern Physics 37: 231-287
- (1995). Optical Coherence and Quantum Optics. Cambridge: Cambridge University Press.
Navarro, Luis, Enric Perez (2004). Paul Ehrenfest on the Necessity of Quanta (1911): Discontinuity, Quantization, Corpuscularity, and Adiabatic Invariance. Archive for History of Exact Sciences 58: 97-141
Pauli, Wolfgang (1923). Über das thermische Gleichgewicht zwischen Strahlung und freien Elektronen. Zeitschrift für Physik 18: 272-286
- (1926). Quantentheorie. Handbuch der Physik 23: 9-23
Planck, Max (1913). Vorlesungen über die Theorie der Wärmestrahlung. Leipzig: Barth.
- (1925). Zur Frage der Quantelung einatomiger Gase. Sitzungsberichte der Preußischen Akademie der Wissenschaften zu Berlin
Rubens, Heinrich (1913). Solvay Conference 1911: Die Prüfung der Planckschen Strahlungsformel im Gebiete langer Wellen. Abhandlungen der Deutschen Bunsen-Gesellschaft 7: 72-76
Sredniawa, Bronislaw (2006). Scientific and Personal Contacts of Polish Physicists with Einstein. Concepts of Physics 3: 385-427
Stark, Johannes (1910). Zur experimentellen Entscheidung zwischen Ätherwellen- und Lichtquantenhypothese, I. Röntgenstrahlung. Physikalische Zeitschrift 10: 902-913
Warburg, Emil (1913). Solvay Conference 1911: Die experimentelle Prüfung der Planckschen Formel für Hohlraumstrahlung. Abhandlungen der Deutschen Bunsen-Gesellschaft 7: 65-71
Wheaton, Bruce R. (1983). The Tiger and the Shark. Empirical Roots of Wave-Particle Dualism. Cambridge, MA: Cambridge University Press.
Wolfke, Karol (1980). Wspomnienia o ojcu, Dr. Mieczysław Wolfke (Recollections on my father, Dr. Mieczysław Wolfke). Postepy Fizyki 31: 551-558
Wolfke, Mieczysław (1911). Über die Abbildung eines Gitters bei künstlicher Begrenzung. Annalen der Physik 34: 277-310
- (1912). Allgemeine Abbildungstheorie selbstleuchtender und nichtselbstleuchtender Objekte. Annalen der Physik 39: 569-610
- (1913a). Zur Quantentheorie. Verhandlungen der Deutschen Physikalischen Gesellschaft 15: 1123-1129
- (1913b). Zur Quantentheorie. Verhandlungen der Deutschen Physikalischen Gesellschaft 15: 1215-1218
- (1914a). Zur Quantentheorie. Verhandlungen der Deutschen Physikalischen Gesellschaft 16: 4
- (1914b). Welche Strahlungsformel folgt aus der Annahme der Lichtatome?. Physikalische Zeitschrift 15: 308-379
- (1921). Einsteinsche Lichtquanten und räumliche Struktur der Strahlung. Physikalische Zeitschrift 22: 375-379
- (1930). Bemerkung zu “Statistische Deutung zur Einsteinschen Ableitung des Planckschen Gesetzes” von R.J. Majumdar und D.S. Kothari in Allahabad. Zeitschrift für Physik 61: 725-726
- (1946a). Über Multiphotone. APAN III-71, 23: 5-12
- (1946b). Über die Mehrfachquanten in der Planck'schen Strahlung. Helvetica Physica Acta 19: 427-429
- (1946c). Sur la possibilité d'un effet photoélectrique des multiphotons. Comptes Rendus 233: 655-657
Footnotes
Einstein always maintained this point of view, as seen in a letter sent to Wolfke in 1946, see sec. (4.4).
Since the text in both publications is identical, we will refer to the more easily accessible 1917 publication only.
“I [Ioffe] tried to build [at that time] a theory of radiation energy analogous to the kinetic energy of gases” (Ioffe 1983, 63). Ioffe further aimed to discuss his “at that time heretical ideas” with Planck and to this end visited him at his resort at Lake Chiemsee in Upper Bavaria at the end of August 1910. Ioffe’s former teacher, Wilhelm Conrad Röntgen (1845–1923), arranged the meeting. Ioffe also notes:
“Seit dem Erscheinen des Aufsatzes von A. Einstein ist eine Reihe von Tatsachen entdeckt und diskutiert worden, die ihre einfachste Erklärung in der atomistischen Auffassung der Strahlung, oder wenigstens ihrer Emission, finden.” Unless otherwise indicated all English translations are by the authors.
These are now called electromagnetic waves.
At that time the German word for momentum was Bewegungsgröße.
Even though in 1910 there was growing evidence that “X-rays and light are manifestations of the same phenomena” only a few, such as Stark, believed this was so (Wheaton 1983, 169).
Because of a mistake in the derivation of Planck’s formula, Wolfke realized only in a subsequent publication (Wolfke 1913b) that
 is identical to Planck’s constant.
is identical to Planck’s constant.
“Die Gleichung bildet die Hauptgleichung des Lichtatoms.”
This remark is important: Planck assumed, within the same paragraph, that the energy of a light quantum is related to a mass through the Newton relation
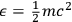 , and not through the relativistically correct relation
, and not through the relativistically correct relation
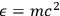 . Therefore, Planck obtained twice the classical value for the radiation pressure as Maxwell did for the first time. (For a detailed derivation of the classical radiation pressure, see (Planck 1913, §58, eq. 64)).
. Therefore, Planck obtained twice the classical value for the radiation pressure as Maxwell did for the first time. (For a detailed derivation of the classical radiation pressure, see (Planck 1913, §58, eq. 64)).
For more details, as well as information on Wolfke’s relationship with Einstein over the years, see (Kiejna 2002).
Swiss Federal Institute of Technology, Zurich.
Letter [from an unknown author, handwritten] of Section VIII from 26 May 1913 addressed to the Chair of the Swiss School Council in Zurich regarding the request for the habilitation of Wolfke: “Professors Einstein and Weiss both agree in their favorable appraisal of the submitted scientific publication and of the professional qualifications and the character of the applicant, and accept the habilitation […].” “Die Herrn Proff. Einstein und Weiss sprachen sich übereinstimmend günstig über die eingereichten wissenschaftlichen Arbeiten, die Vorbildung und die Persönlichkeit des Gesuchsstellers aus, und begrüssten die Habilitation […].”, III–71.21, 23, APAN.
We can only guess why Wolfke took so long to publish on the light quantum problem. Einstein had already left Zurich in 1913, and during World War I, Wolfke and his family (wife and two children) faced severe economic problems with no regular income (Wolfke 1980).
“[…] die schwarze Strahlung aus […] voneinander thermodynamisch unabhängigen Teilstrahlungen besteht […].”
Different from the notations of the publications to be discussed, we additionally label the expansion coefficients and their associated quantities with the frequency
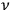 to which they refer. This is necessary for Appendix 4, in which processes that change the frequency of light molecules, such as the Compton effect, are treated.
to which they refer. This is necessary for Appendix 4, in which processes that change the frequency of light molecules, such as the Compton effect, are treated.
Jun Ishiwara (1881–1947) discussed this expansion as early as 1912 (Ishiwara 1912).
To follow the mathematical manipulations throughout this manuscript more easily, the following identities are useful:
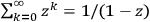 ;
;
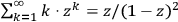 ;
;
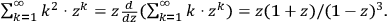
“[…] daß die Hohlraumstrahlung, vom Standpunkt der Einsteinschen Lichtquantenhypothese aus betrachtet, aus voneinander räumlich unabhängigen Lichtmolekülen
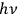 ,
,
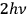 ,
,
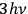 , […] zusammengesetzt ist.”
, […] zusammengesetzt ist.”
Following Wolfke, for this presentation we rewrote all quantities that depend on volume and frequency such that their value per volume,
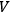 , and frequency interval,
, and frequency interval,
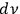 , is always quoted. Thus,
, is always quoted. Thus,
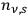 is really a number density per frequency interval,
is really a number density per frequency interval,
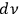 , and not, as Wolfke mistakenly called it, the numbers of the various light molecules. In all the other publications discussed here, the
, and not, as Wolfke mistakenly called it, the numbers of the various light molecules. In all the other publications discussed here, the
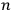 are always connected to the number of light molecules, but refer differently to the volume and the frequency interval. For example, in Bothe’s early manuscript (Bothe 1923), the
are always connected to the number of light molecules, but refer differently to the volume and the frequency interval. For example, in Bothe’s early manuscript (Bothe 1923), the
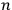 denote the number of light molecules per frequency interval, even though this is not evident at first glance. In his last publication, Bothe defined
denote the number of light molecules per frequency interval, even though this is not evident at first glance. In his last publication, Bothe defined
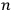 as a dimensionless number (Bothe 1927b), as did de Broglie in his brief publication (de Broglie 1922b) and Darrigol in his review article (Darrigol 1991).
as a dimensionless number (Bothe 1927b), as did de Broglie in his brief publication (de Broglie 1922b) and Darrigol in his review article (Darrigol 1991).
In his paper, Wolfke discusses the inverse ratio.
“Wir sehen daraus, wie mit zunehmender Strahlungsdichte eine Assoziation von Lichtquanten zu immer komplizierteren Lichtmolekülen stattfindet, bis schließlich die Quanten bei sehr großen Strahlungsdichten, im Gültigkeitsbereich des Jeans-Rayleighschen Strahlungsgesetzes, sich zu einem Kontinuum zusammenballen! Umgekehrt, mit abnehmender Strahlungsdichte dissoziiert das Strahlungskontinuum in immer einfachere Lichtmoleküle, bis es sich schließlich in diskrete Lichtatome auflöst!”
De Broglie did not use the quantity
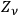 explicitly.
explicitly.
A detailed discussion of de Broglie’s concerns can be found in (Bergia et.al. 1985).
Details on Bothe’s vita up to the 1920s and his experimental achievements in the study of the wave-particle duality of light during the 1920s can be found in a recent article entitled “Walther Bothe’s Contributions to the Understanding of the Wave-Particle Duality of Light” (Fick and Kant 2009).
“The Spatial Energy Distribution of Black-Body Radiation.” The Archive of the Max Planck Society in Berlin (AMPG) retains, at the back of another manuscript, a handwritten manuscript (Bothe manuscript, III/6/104,1, AMPG) which coincides in large part with the printed version of Bothe’s publication in the Zeitschrift für Physik. The differences in the printed version are marginal, as far as the content is concerned. On a few additional pages (microfilm pages 1211, 1213, 1224), Bothe also discusses the question of whether the structure of radiation emitted by a black body changes under processes that do not change the temperature of the radiation (reflection, refraction, absorption, etc.). He concluded that at his time such questions could not be answered experimentally.
See also the end of this section.
Without a lack of generality, we choose the statistical weights of the states
 and
and
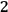 to be the same and equal to one, since they will not appear in the final results. This is why the
to be the same and equal to one, since they will not appear in the final results. This is why the
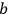 -coefficients for induced transitions and for absorption of a light quantum are equal here.
-coefficients for induced transitions and for absorption of a light quantum are equal here.
“Beide [Quanten] sind scheinbar gekoppelt; nur scheinbar deshalb, weil in Wahrheit keine Kräfte zwischen ihnen wirken, die Dissoziationsarbeit […] ist Null. Wird etwa eins der beiden Quanten absorbiert, so wird das Schicksal des anderen hierdurch in keiner Weise beeinflusst; dies ist eine Konsequenz der Annahme, dass die Wahrscheinlichkeit eines Einstrahlungsprozesses einfach proportional der mittleren räumlichen Dichte der Quanten ist. Wir werden deshalb besser von Quantenpaaren sprechen. Gehört das auslösende Quant selbst schon einem Paar an, so entsteht ein Tripel, usf.”
In the manuscript, Bothe denotes by
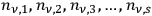 the number of light quanta
the number of light quanta
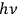 which form singlets, pairs, triplets, … respectively. This definition differs from the one used by Wolfke (1921), and also from the definition used later by Bothe himself (1924). In what follows, we use Wolfke’s definition (1921) of the
which form singlets, pairs, triplets, … respectively. This definition differs from the one used by Wolfke (1921), and also from the definition used later by Bothe himself (1924). In what follows, we use Wolfke’s definition (1921) of the
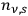 . It relates to the definition in the work discussed here through the relation
. It relates to the definition in the work discussed here through the relation
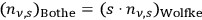 . Thus, here, the fraction of the total radiation density
. Thus, here, the fraction of the total radiation density
 , which belongs to
, which belongs to
 -fold quantum multiples, is
-fold quantum multiples, is
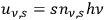 .
.
As mentioned in footnote 30, we chose without lack of generality the statistical weights of states
 and
and
 to be the same and equal to one, since they anyway will not appear in the final results.
to be the same and equal to one, since they anyway will not appear in the final results.
Bothe (ca. 1925). Zur Struktur der Strahlung, unpublished manuscript, AMPG III/6/105.4.
It is surprising that Bothe cited Wolfke, even though Wolfke did not discuss the energy variation in his paper at all.
“Die Einsteinsche Herleitung der Strahlungsformel (Einstein 1917) zeichnet sich bekanntlich durch außerordentliche Anschaulichkeit aus. Versucht man diese weiterzubilden, ohne ihr diesen Charakter zu nehmen, so gelangt man zwangsläufig zu der merkwürdigen Vorstellung, dass im stationären Strahlungsfelde die Lichtquanten im allgemeinen nicht unabhängig voneinander, sondern zu Aggregaten vereinigt sind. Durch Berücksichtigung dieser Assoziationen der Lichtquanten gelangt man erst zum richtigen Ausdruck für die Energieschwankungen im Strahlungsfeld (Bothe 1923; Wolfke 1921). Leider ist es bisher nicht gelungen, von diesem Punkte aus die Brücke zu der klassischen Wellentheorie der Strahlung zu schlagen, z.B: die Anzahl der Freiheitsgrade eines Strahlungsvolumens richtig anzugeben, oder gar die Interferenzen zu deuten.” (The bibliographic references in parentheses were footnotes in Bothe’s original manuscript).
Since the number density of the
 -fold light multiples differs in definition from the ones of the previous section, we denote them now with a gothic
-fold light multiples differs in definition from the ones of the previous section, we denote them now with a gothic
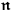 instead of a latin
instead of a latin
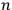 .
.
For an early interpretation of Bothe’s choice, see Jordan’s (1928, in the very last paragraph of section I) discussion.
“Der Summand
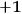 in der Klammer ersetzt gewissermaßen die spontanen Übergänge, da er z.B. auch nullquantigen Aggregaten die Auslösung von Emissionsprozessen
ermöglicht.”
in der Klammer ersetzt gewissermaßen die spontanen Übergänge, da er z.B. auch nullquantigen Aggregaten die Auslösung von Emissionsprozessen
ermöglicht.”
This fact was, for example, discussed highly pedagogically in volume III of the Feynman Lectures on Physics (Feynman et.al. 1965, Chap. 4.4, Emission and absorption of photons).
One year later, Reinhold Fürth (1893–1979) discussed the same issue in other contexts (Fürth 1928a; 1928b).
We discuss the physical implications of this assumption in the following section, after obtaining formal results (4.3.3).
Einstein used this kind of reasoning for the first time in his 1911 talk at the Solvay Conference (Einstein 1913).
“Dies ist das neue Verteilungsgesetz der Quantenaggregate. Aus ihm ergibt sich leicht die gesamte Strahlungsenergie
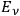 von der Frequenz
von der Frequenz
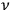 […] d.i. die Plancksche Formel.”
[…] d.i. die Plancksche Formel.”
“Wir können hiernach also jedes Quantenaggregat in der Hohlraumstrahlung deuten als die Energie einer Eigenschwingung des Hohlraums.” Sentence underlined on p. 10 in Bothe’s manuscript.
Quite recently one of the authors (D. Fick) presented an analysis of Bothe’s 1925 heuristic assumption (Fick in print), on which sections 4.3.1 and 4.3.2 are based.
For details, see the extended report by Fick and Kant, “Walther Bothe’s Contributions to the Understanding of the Wave-Particle Duality of Light” (Fick and Kant 2009).
A brief report on a talk by Einstein presented at Berlin University (renamed Humboldt University in 1948) entitled “Theoretisches und Experimentelles zur Frage der Entstehung des Lichtes” (Anonymous 1927) explicitly mentioned this experiment. However, there were also critical questions concerning its relevance (Kirchner 1930, 467–468).
Bothe (ca. 1926). Lecture Notes, unpublished, AMPG III/6/105.3.
See also (Jordan 1929), in particular, the discussion of eqs. 9 and 10.
To make this clear, we deliberately denoted the two contributions to eq. (4.33) with “wave” and “particle” and not as Bothe did with “wave” and “quantum.” See also “Reconstruction of and commentary on Jordan’s derivation of Einstein’s fluctuation formula” in (Duncan and Janssen 2008, sec. 3).
For an extended introduction, see the lucid description of the physics involved in sec. 4.2 of (Mandel and Wolf 1965).
References to these experiments and as well its semiclassical as its field theoretical treatment can be found in (Mandel and Wolf 1995, sec. 9.9 and 14.6.1).
Because of their briefness and beauty, we repeat here von Laue’s arguments, which refer partly to Planck: “The entropy
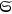 of a system is […] connected with its probability
of a system is […] connected with its probability
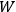 through the equation
through the equation
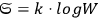 . For two subsystems
. For two subsystems
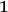 and
and
 , which add up to the total one, the partial entropies are accordingly:
, which add up to the total one, the partial entropies are accordingly:
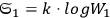 and
and
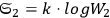 . Out of these three equations, the addition theorem for entropies
. Out of these three equations, the addition theorem for entropies
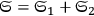 ensues if and only if
ensues if and only if
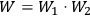 . A complete independence of each of the two systems would be a necessary and sufficient condition. […] coherent light bundles are, however, not independent of each other at all. Therefore the addition theorem is not valid” (Laue 1906, 374, fn. 4). “(Die Entropie
. A complete independence of each of the two systems would be a necessary and sufficient condition. […] coherent light bundles are, however, not independent of each other at all. Therefore the addition theorem is not valid” (Laue 1906, 374, fn. 4). “(Die Entropie
 eines Systems ist […] mit seiner Wahrscheinlichkeit
eines Systems ist […] mit seiner Wahrscheinlichkeit
 durch die Gleichung
durch die Gleichung
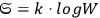 verknüpft. Für zwei Teilsysteme, aus denen das ganze bestehen soll, gilt entsprechend
verknüpft. Für zwei Teilsysteme, aus denen das ganze bestehen soll, gilt entsprechend
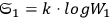 und
und
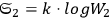 . Aus diesen drei Gleichungen folgt das Additionstheorem dann und nur dann, wenn
. Aus diesen drei Gleichungen folgt das Additionstheorem dann und nur dann, wenn
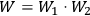 ist; notwendige und hinreichende Bedingung dafür ist, dass die beiden Teilsysteme voneinander vollkommen unabhängig sind, […]. Kohärente Strahlenbündel sind aber nicht voneinander unabhängig, also gilt für sie das Additionstheorem nicht.)”
ist; notwendige und hinreichende Bedingung dafür ist, dass die beiden Teilsysteme voneinander vollkommen unabhängig sind, […]. Kohärente Strahlenbündel sind aber nicht voneinander unabhängig, also gilt für sie das Additionstheorem nicht.)”
Further work on this topic was published at around this time by von Laue (1907a; 1907b) and Ehrenfest (1925, 364, fn.1). See also sec. 4.7 “Entropy of an Optical Field” in (Mandel and Wolf 1965) for further historical information.
“Bothe schuf das einigermaßen neue Konzept der Lichtmoleküle und gelangte so zur Planck’schen Formel.”
Wolfke to Einstein, 13 December 1925, 23 507, Einstein Archive Online.
Wolfke to Einstein, 27 and 29 December 1930, 23 517 and 23 519, Einstein Archive Online.
“[…], dass es auf Grund der Bose-Einsteinschen Statistik nicht zulässig ist das Strahlungsfeld, als aus “Mehrfachquanten” bestehend, zu interpretieren” (see footnote 67).
Wolfke to Einstein, 29 December 1930, 23 521, Einstein Archive Online.
Einstein to Wolfke, 10 April 1931, 23 522, Einstein Archive Online.
“Ihr Argument hat zu erst großen Eindruck auf mich gemacht. Aber ich finde eine Schwierigkeit.”
This letter prompted us to explicitly show that Bothe’s interpretation of the
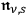 as quantum multiples, including the
as quantum multiples, including the
 ones, is in accordance with Boltzmann statistics.
ones, is in accordance with Boltzmann statistics.
“About Multiphotons”, APAN: III–71,23, 5–12. According to the then general use of the word “photon,” rather than “light quantum,” he used the phrase “multiphoton” rather than “light molecule” (Wolfke 1946a).
Wolfke neglected—for whatever reason—Bothe’s (1927b) dynamical treatment and thus the fact that Bothe obtained the same result almost two decades earlier.
APAN: Wolfke manuscript, 1941, III–71, 20, 10–11. In a report to his authorities in Warsaw, Wolfke writes: “On 8. IX. [1946] I lectured at a meeting of the Schweizerische Naturforschende Gesellschaft in Zurich ‘On multiple quanta in Planck’s radiation,’” an abbreviated version of which was published in 1946 (Wolfke 1946b).
Wolfke probably had personal relations with de Broglie, who visited Wolfke’s institute in Warsaw in 1933 (Wolfke 1980).
APAN: III–71,20, 10–11.
Einstein to Wolfke, 17 July 1946, APAN, III–71,24, 7.
“Beim ersten Augenblick könnte diese Forderung befremdend erscheinen, weil hier eine Wechselwirkung von Strahlenbündeln mit unter Umständen weit verschiedenen Frequenzen angenommen wird.”
For further more recent discussions, see (Lewis 1973; Lanyi 2003).
We take this opportunity to point to Pauli’s article in Handbuch der Physik, where he discussed the heat balance between atoms and radiation in much more detail in sec. I.2. “Wärmegleichgewicht zwischen Atomen und Strahlung” (Pauli 1926, 9– 22).
As before,
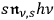 denotes the fraction of the total radiation density that belongs to
denotes the fraction of the total radiation density that belongs to
 -fold light multiples, see sec. (4.3.2).
-fold light multiples, see sec. (4.3.2).
All quantities are defined within the normal coordinate system of the individual process.

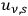 following Wien’s radiation law.
following Wien’s radiation law.
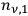 . Inserting it into eq. (
. Inserting it into eq. (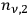 , and so on.
, and so on.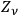 in the equation below, see eq. (
in the equation below, see eq. (