2 Learning from Kushim About the Origins of Writing and Farming

Learning from Peter Damerow

Peter Damerow was a man of relentless curiosity, of great inventiveness, and of remarkable intellectual courage. His investigations into the origins of mathematics were initially inspired by his broad-ranging philosophical interests, and also by his engagement with educational science. In the early 1980s, he began to follow the traces of such great trail blazers in the exploration of ancient mathematics as Otto Neugebauer and François Thureau-Dangin, turning to the historical sources, in particular to the early documents of writing and calculating from Mesopotamia.

But at the time, the earliest documents, the so-called proto-cuneiform texts, were still generally disregarded because they seemed to provide neither important literary or historical documents, nor evidence of an advanced state of mathematics. Rather, they mostly dealt with such mundane issues as accounting and administration. In addition, they were copious, too numerous indeed, or so it seemed, to individually warrant the careful philological treatment typical of the interests and prevailing methods of philological analysis. But Peter was a resourceful man and times were changing. He was convinced that computer technology would facilitate an analysis of these proto-cuneiform texts and thus became, simultaneously, one of the pioneers of what are now called the digital humanities.

Peter was also a generous man and a master in community building. As a student of physics and of history of science in Berlin, I had the opportunity to closely follow Peter’s remarkable career as one of the pioneers in the study of early writing and calculating. I participated in workshops he organized on Babylonian mathematics, which soon turned into a gathering-place of the international community of experts in Mesopotamian culture, as well as of scholars worldwide who were interested in the emergence of writing and mathematics. Many of the epistemological insights gained in this context have profoundly shaped my own work. I am deeply grateful to Peter, my mentor and close friend, with whom I collaborated on many other topics. The following text is a tribute to his extraordinary achievements in the fields of early writing and mathematics, from which I have learned so much.

Cereals, Beer, History

While history usually is distinguished from prehistory by the existence of writing, the actual introduction of writing was probably quite uneventful.¹ The Babylonian administrator Kushim could not have known that his inscriptions into soft clay would be thoroughly studied some 5,000 years later, literally inscribing him and the writing system he used to keep an account of his granular assets into the more-than-human history of humankind.

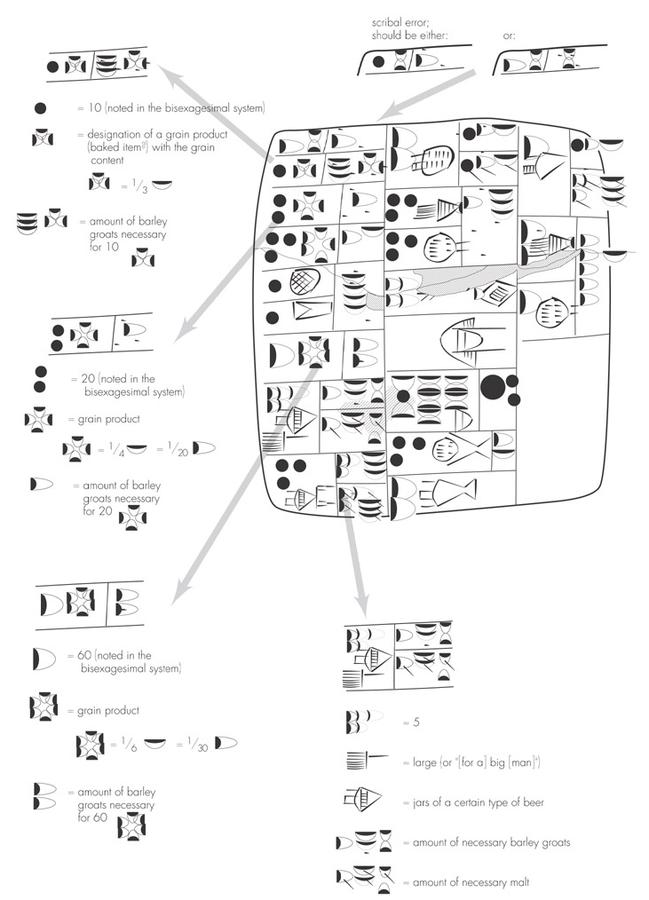
Kushim, or the scribe who was assigned to note down the calculations for him, was simply going about his duties as a SANGA: the head of an administrative unit (a term later used as a designation for a priest). Kushim was in charge of a large facility that stored the basic ingredients for the production of beer and other cereal commodities. This was no medium-size enterprise: at one point, he had to administer around 135,000 liters of barley. The tablet printed above contains calculations of the ingredients needed to produce nine different cereal products and eight different kinds of beer. The scribe working for Kushim calculates, for instance, the amount of barley groats needed to produce thirty units of a certain cereal product, the amount of barley groats and malt needed to produce five jugs of a certain beer, and the amount of barley needed for 1,800 cereal rations. In one of the calculations, the sign for “1” is written erroneously for the sign for “10,” but otherwise the calculation is correct.²

Kushim’s duties formed part of a larger administrative context of the earliest Mesopotamian cities. The administration was responsible for collecting and redistributing the agricultural products on which their wealth was mainly based. It was the agricultural surplus of this production that had enabled the development of the hierarchically stratified societies of these cities, including the division between manual and intellectual labor that gave Kushim his position in the first place. While he and his like planned the labor, and appropriated and administered its fruits, others had to do the real work. No wonder, then, that the intellectual work of Kushim, as documented by twenty-one extant clay tablets, was concerned exclusively with the economic aspects of contemporary life.

The First Cities

Human history depends on ecological conditions, but it also hinges crucially on knowledge. In the fifth millennium BCE, southern Mesopotamia—the Babylonian plain lying between the rivers Euphrates and Tigris—was a landscape of swamps and marshlands suffering from regular fluvial inundations which rendered it essentially inhospitable for large-scale agricultural regimes. A climatic change that led to a reduction of precipitation during the fourth millennium BCE changed this situation. The sea level of the Persian Gulf began to drop so that the swamps and marshlands eventually became suitable for farming. Claiming that the situation had become favorable for such activities does not mean that they could actually take place without the knowledge and technology needed to turn this landscape into an agricultural resource.

Toward the end of the fourth millennium, when the early civilization in southern Mesopotamia arose, eventually giving rise to large cities and empires, such knowledge had become available. The capacity to produce food from arable land had been generated over the course of the Neolithic Revolution some 5,000 years earlier. At the turn from the fourth to the third millennium, however, a new challenge emerged as water became increasingly sparse and had to be transported to the cultivated lands. The response of the early settlers to this challenge was the construction of ever more sophisticated irrigation channels, a collaborative achievement that deeply marked the further evolution of Mesopotamian societies.³ At this point, the relationship between humans and their environment had been reversed; rather than being determined, or at the very least constrained by environmental conditions, humans were now actively transforming and exploiting their environment.

Alien Symbols

But how did Kushim come up with the glorious and very consequential idea to invent writing on what might have been a sunny day in southern Mesopotamia in 3000 BCE? Actually, he didn’t. The texts that Kushim and his scribes wrote are not actually texts, since they deal with quantitative relations between different items, but have more in common with the spreadsheets used in modern administrative contexts. But they are not really spreadsheets either. The main difference here is that what Kushim used to determine the amounts of barley and malt needed for the final products were not numbers. Neither he, nor anyone else of his time, knew either writing or arithmetic. He used something else, elements of symbolic systems that we designate, for lack of a better term, as “proto-writing” or “proto-arithmetic.” Kushim’s symbols signified neither sentences, nor calculations with abstract numbers in the sense of a manifestly context-independent arithmetic. They simply represented what he was concerned with: not language, but rather administrative acts dealing with specific products of the society of which he was a part.

On Kushim’s tablet, five different numerical systems are used: one for cereal products, another for beer containers, and three different systems for the cereals themselves. In other words, the quantification of these objects was linked to their quality, while an abstract system of numbers designating quantity independent of quality and context did not yet exist. Similarly, the non-numerical signs used on these clay tablets were not elements of a writing system aiming at a rendition of human language, but just representations of certain administrative categories. We are thus confronted not with a primitive version of modern writing or mathematics, but with an evidently efficient administrative tool of the archaic Mesopotamian society, a symbolic system, and a way of thinking in its own right that is not reducible to our modern categories.

This presents a typical scenario of which scholars in the humanities are very fond: a peculiar way of thinking that differs from our own modern way, situated in a remote place at a remote time, which can only be understood on its own terms by taking into account local contexts and practices. We do not even run the risk of interfering with this alien system of thinking since we can hardly ask Kushim about it. To understand it, we must simply rely on the work of archeologists, Assyriologists, and historians, in this case on the pioneering studies of Peter Damerow, Robert K. Englund, and Hans Nissen on archaic bookkeeping practices. Kushim’s clay tablet, which is being considered here, is just one of many thousands documenting the Mesopotamian world. They are meanwhile openly available on the Internet thanks to the efforts of the Cuneiform Digital Library Initiative (CDLI).⁴

The Great Transitions

Although it is still favored among scholars in the humanities, there is a problem with this kind of focus on the local. As is clear from the overwhelming record of historical documents from Mesopotamia, writing in the modern sense as a more or less durable representation of human language—in this case cuneiform writing—as well as arithmetic in the sense of operations with abstract numbers did eventually emerge from the exotic symbol system used by Kushim. Where exactly did this system come from in the first place, and how did its transformation into writing and arithmetic take place?

These questions more generally concern the way in which human history gives rise to major transitions, such as the origins of tool use and material culture, the origin of symbolic thinking and of language, the emergence of agriculture, the development of urbanization and the invention of writing, the spread of religions, and the rise of science, or the industrial and digital revolutions. The Anthropocene is characterized by the lasting global impact of human interventions. Essentially, this impact has manifested itself since the first use of modern industrial resources or, more articulately, since the beginning of the Great Acceleration in the 1950s. The Anthropocene in fact started much earlier when humans began to transform their environment during the Neolithic Revolution (or rather during the several Neolithic Revolutions that occurred in various places around the globe) and when their knowledge became part of a long-lasting process of sedimentation in consequence of the invention of writing. If we want to understand how this global impact took place and also how we can shape it in the future to ensure human survival, we have to find out more about the relation between the long-term cumulative effect and the contingent character of human actions and knowledge, which always depends on chance constellations and local circumstances.

Exploring the Limits of Symbolic Representations

In the second half of the fourth millennium BCE, the modest accounting techniques that had been developed earlier in the context of the rural economy of Mesopotamia were extensively exploited in the administration of the emerging city-states. These city-states represented higher-order structures with centralized administrative functions within a network of smaller settlements. Among the traditional accounting techniques were small clay tokens of different shapes serving as symbolic representations of objects and used for representing and controlling their quantities; seals were used to represent certain administrative acts. The exploration of these given means, serving as external representations of administrative knowledge in the context of an expanding economy, eventually led to a transformation of the traditional symbolic culture. The potential of existing tools of symbolic representation was exploited to its limits. This led, for instance, to a proliferation of accounting practices, which originally had played only a minor role in the context of rural communities.

A critical turning point was when these two elements of traditional accounting techniques—the counters used for keeping track of the quantities of administered objects and the seal impressions documenting administrative acts—came to be represented within a single medium: a clay tablet of the kind found in Kushim’s office. The seal impressions, in particular, carried information about the administrative and societal context that determined their meaning. They testified to property, legal acts, or socially correct behavior. The two elements were initially also integrated in the form of sealed hollow clay balls (bullae), containing certain combinations of clay counters. Sometimes the combinations of tokens inside were represented by marks on the bullae’s surface. In principle, sealed clay tablets served the same function but were easier to handle than the bullae. In any case, two initially separate accounting techniques thus became integrated into a new form of external representation whose enormous potential could and would be explored in the sequel. As we have seen, the emergence of this new form of representation was itself the result of an exploration in response to the challenge of an expanding economy.

Challenging Objects

This is a familiar feature of the development of networks of human actors embedded in environments that, at the same time, are transformed by them. They may react to external challenges, assimilating them to their existing internal structures, that is, to the mental frames of the actors and the social structures of their interactions, by expanding and differentiating them. This, in turn, creates the preconditions for their reorganization and the accommodation of their internal structures to the new situation. This internalization of external challenges by creating new regulatory regimes is, in a sense, the complementary process to the externalization of a network’s internal structures in terms of the creation of a material culture and of external representations of knowledge and social institutions, in short, the complement to what biologists call “niche construction.”⁵

The so-called numero-ideographic tablets were transition-stage tablets, unearthed in Kushim’s Uruk as well as in ancient Iran. They contained representations of rudimentary numerical signs together with an initial set of a dozen or so non-numerical signs designating counted or measured objects. Representing an early stage of proto-writing and proto-arithmetic, they became the starting point for the exploration of new forms of information storage and processing in the archaic period of the Mesopotamian society. The tablets could hold more information than the earlier administrative techniques and this information could be more flexibly and efficiently structured. For instance, it was now easy to invent new signs to denote new semantic categories. Conversely, the existing economic and administrative activities were shaped by these new techniques of representation. The new signs and structures for information processing were standardized, giving rise to the proto-cuneiform administrative texts of the kind generated by Kushim’s office. As a result of this development, the proto-cuneiform administrative texts became the external representations of a mental model of the accumulation and distribution of resources and products in the Babylonian administration. This mental model—the internal cognitive structure of the actors—was in turn generated by a reflection on the specific actions constituting this administration, including actions undertaken using these external representations.

The next step in the development of writing was shaped by a fundamental property of external representations: that the range of their possible applications is larger than the specific goals for which they had initially been introduced. The potential of the proto-cuneiform texts to represent mental constructions reached far beyond the limited field of application within Babylonian administration. In its most evolved form, reached at least by around 2600, it also included the possibility of representing spoken language and the abstract numbers of mathematics. A further characteristic feature of the development of a system of knowledge, however, is that such possibilities typically occur only as a side effect of its mainstream applications. It is also characteristic that the foundational role of these marginal applications as being constitutive of a new developmental stage is only realized once a new perspective is introduced, often triggered by a new external context. The recontextualization of a system of knowledge thus becomes a major driving force for its reorganization.

The Introduction of a New Perspective

In the case of the emergence of writing, the further development of the proto-cuneiform writing system was at first entirely governed by its function within the Mesopotamian administration and by its growing sophistication. But precisely this sophistication also created contexts in which new applications of the system could arise and be considered from a new perspective, at some distance from the sphere of primary applications. One such context was education (Nissen 2011). Indeed, the growing complexity of the system required institutional support for its transmission from generation to generation. Schooling implies a separation of the cognitive means of administration from their immediate context of application and thus opens up a perspective in which the potential of these cognitive means could be explored independently of the constraints of their application to solve concrete administrative problems. Texts documenting this explorative quality produced in such educational contexts have indeed been preserved. What have also been preserved are so-called lexical lists documenting the concern of scribes with the standardization and semantic classification of signs. They even contain signs that seem to have been specially invented for teaching purposes.

The role of education provides a good example for the emancipation of a system of knowledge from its embedding within concrete contexts of application. But there were also other factors that may have worked similarly toward a recontextualization of the existing system of proto-writing and proto-arithmetic, thus introducing a more reflective perspective on this system that favored the discovery of the possibility to repurpose it for representing language and abstract numbers. The expansion of the system, which had to include more and more names of persons, institutions, and objects, may have triggered the search for a principle to introduce new signs and sign combinations, rather than relying on ad-hoc solutions, a search that may have led to the coding of names by phonetization. Applications of the system outside the strictly economic and administrative context, for instance to support the memorization of orally transmitted texts, must have also contributed to its recontextualization.

The Strength of Weak Ties

Further recontextualization factors contributing to recognition of the system’s potential to represent language, and not just specific mental models rooted in a local administrative context, may have been the emergence of cuneiform writing within a multilingual context, the adaptation of the system to more than one language, and also the parallel development of other writing systems in the larger region. The latter provides a good illustration of what has been called “the strength of weak ties” within networks (Granovetter 1973) because the exchange even of incomplete information about writing systems or just stimulus diffusion of the knowledge of such systems may have triggered developments in marginal areas of the network that were by their very nature independent of the contexts from which they originated. Similar mechanisms affected the development of the abstract concept of number and of arithmetic in the sense that operations with these numbers were independent of the quality of the quantities with which calculations were performed.

What is Abstraction?

In the context of the genesis of the abstract number concept, however, we see even more clearly yet another mechanism at work, which we may designate as “iterative abstraction” what Jean Piaget called “reflective abstraction.” The reflection on actions with external representations, such as the clay tokens used for accounting, in the early stage generates knowledge of a higher order of abstraction than the knowledge to which these external representations originally referred. The results of such reflections may again be externally represented.

The clay tokens were simply representations of the counted objects. But representing the results of establishing a one-to-one correspondence between these counters and the counted objects in the form of numerical signs on clay tablets turned these signs into a representation of knowledge on a higher order of abstraction. On this level, the relation between the individual quantities and their sum total, for instance, can now be expressed in terms of a permanent relation between signs, whereas on the level of the original objects or the counters, it is just given by a temporal succession in which the parts are no longer distinguishable once the whole is established, for instance, after putting all fruits to be counted into one basket. Similarly, operations with these numerical signs, for instance replacing 10 signs of value “1” with one sign of the larger value “10,” no longer correspond to actions with the original objects, but to operations on a meta-level with regard to the primary actions.

Iterative abstractions such as those that eventually gave rise to the abstract mathematical concept of number ultimately depend on the material actions from which they originate, such as the concrete actions of counting material objects with the help of counters or number signs. Iterative abstractions are a constructive process in which novel cognitive structures are built by reflecting on operations with specific external representations such as language, counters, or mathematical symbols. These external representations may in turn embody previously constructed mental structures so that a potentially infinite chain of abstractions is created. It may appear as if this chain of abstractions gives rise to a predetermined hierarchy of steps leading necessarily from actions with concrete objects to ever higher-order mental operations of universal validity. This, however, is not the case. The historical development of iterative abstractions is in fact highly path-dependent, contingent as it is on a series of concrete historical experiences, as is apparent in the case of Kushim’s accounting activities.

Cultural Evolution and Creativity

In this explanation of the emergence of writing and the genesis of abstract concepts, there is thus no hidden determinism at work, no teleology in the sense of progress toward a pre-established goal of the development. Everything is shaped by local contexts, by more or less accidental environmental, social, and cultural conditions, by chance constellations and, above all, by human choices. There were indeed other trajectories of the emergence of writing and other pathways along which abstract concepts were formed in other parts of the world and at other times, and they were probably shaped by different local conditions.

On a more general level, however, we still recognize in the story of Kushim the way in which human actions are not only constrained by given contexts, including the conditions they have created themselves, but also how in principle knowledge is created that offers humans, in any given historical situation, a specific freedom to choose their next steps. The invention of writing, for instance, was a step well prepared by a 1,000-year development in which all the pieces of the puzzle were assembled, yet it was a creative human invention that resulted from a deliberate reflection on these pieces. The rapidity of the last step to establish writing as a new means of representation replacing earlier techniques testifies to the autonomous, emancipatory, and intentional character of this act.

The emergence of writing, on the other hand, is clearly also a history of the gradual accumulation of knowledge, a process of sedimentation of action potentials over time, incorporated, above all, in the transmission and enrichment of material culture. At the same time, it is a history of the ever wider spread, or, as one might say, of the “globalization” of these action potentials in space and of the increasing density of links within an expanding network of interactions (Renn 2012). It is therefore more than plausible to describe this history, with its path-dependence, its cumulative and self-referential character, as an evolutionary process. But this history can only be adequately conceived as a form of cultural evolution if the autonomous character of knowledge is recognized as one of its most fundamental features (Richerson and Christiansen 2013).

Beyond the Case of Writing

The case of the invention of writing, it may be objected, is not an appropriate basis for making such far-reaching claims about cultural evolution. It specifically concerns, after all, an epistemic transformation, a development of knowledge, or even more precisely, the emergence of a new medium of representation within a larger context of societal processes such as urbanization, upon which we have hardly touched. These more fundamental processes had established the division of intellectual and manual labor in the first place, as well as the special role of administrative knowledge as knowledge about the organization of production, that is, as a particular form of Herrschaftswissen (social control). The result was a specific economy of knowledge with its own structures regulating the production and dissemination of knowledge, separate from the structures of society at large. In earlier periods, one may suppose that knowledge was directly incorporated into contexts of action, with language essentially being the only means of representing knowledge independently from such contexts, while symbols did not yet possess the specific function for manipulating knowledge that they acquired over the course of the emergence of writing (Damerow and Lefèvre 1998).

It seems clear, on the other hand, that knowledge (not abstract knowledge, of course, but knowledge implicit in actions) must have played a fundamental role also in the achievements of much earlier periods, as well as in those domains of any society that are not penetrated by a specialized economy of knowledge—and such domains evidently exist even today. What role did knowledge play, for instance, in the Neolithic Revolution, in the success story of agriculture, including the great irrigation projects, on which the achievements of Kushim’s society were ultimately based? The great architectural projects, for instance, not only in the period immediately following the Neolithic Revolution, but also those of much later times, well into the modern period, are, in any case, largely based on knowledge that is not documented by writing or any other specialized symbolic representations. Such knowledge remains implicit in the structures of cooperative action that societies capable of realizing such ambitious projects build (Renn, Osthues, and Schlimme 2014). This does not imply, however, that such structures have no history. On the contrary, a history of cultural evolution in consideration of the fundamental role of knowledge must also include the development of such cooperative, action-implicit systems of knowledge.

The Neolithic Revolution

The evolutionary dynamics of the Neolithic Revolution conceived in these terms display remarkable similarities to the emergence of writing. It must be stressed, however, that just as there may have been many pathways to writing, there were certainly also many routes to food production in different parts of the world. Here we will concentrate on the emergence of food production in the Fertile Crescent. Developed agriculture is a comprehensive subsistence strategy involving intensive human labor. It represents an economic system by which human societies produce a large part of their food and other necessities from domesticated plants and animals. Domesticated plants such as cereals are adapted to human nutritional needs and even rely on human intervention for their reproduction. Farming based on domesticated plants and animals is as much a distinctive developmental stage, different from earlier subsistence strategies, as writing is in the sense of a representation of language as a distinctive developmental stage of what we have referred to as proto-writing.

In the history of the Neolithic Revolution, we can indeed identify an equivalent to such an earlier stage, whose expansion eventually gave rise, as with proto-writing, to a framework that channeled the development toward a full-scale agricultural economy. Long before humans began to sow harvested seeds, they practiced various forms of landscape management cultivating, for instance, wild cereals and pulses by tilling the soil.⁶ Unlike fully developed agriculture, pre-domestication cultivation in the sense of the manipulation of wild plants and animals did not itself constitute a complete subsistence strategy, but only one component of such a strategy. It evidently existed for a very long time in human history, but played only a more or less marginal role for food production. It certainly was not motivated by the later outcomes of domestication, but constituted an activity with its own rationale and dynamics. In particular, landscape management represented, just as proto-writing, a highly local and contextualized activity. Only with the establishment of mature agriculture was it possible to reach a somewhat greater independence from local ecological conditions. The role of landscape management and cultivation in forming a scaffold for the later emergence of agriculture is another example that throws new light on the principle that the range of applications of a given means is always larger than the intentions for which they had been originally employed. This may even apply literally to some of the instruments employed in early farming.⁷

Cultivation and Sedentariness

At least in the Fertile Crescent, there were several reasons why pre-domestication cultivation did not remain marginal. Ecological conditions in particular encouraged sedentariness, which favored the extension of cultivation practices bound to local environments. Given the investment of labor in cultivation practices, such local pre-domestication cultivation practices in turn stabilized sedentariness, thus creating what has been called the “labor traps” along the protracted trajectories leading to domestication (Fuller, Allaby, and Stevens 2010). This mutual reinforcement is similar to the case of writing in which the extension of symbolic practices, fostered by the administrative needs of Mesopotamian society, led to an exploration of the inherent potential of these symbolic practices, which in turn stabilized the administration constituting the institutional context of this process. Pre-domestication cultivation in the context of sedentariness thus played a similar role for the emergence of farming as proto-writing did for the invention of writing in the context of administration.

Also similar to the case of writing, globalization effects may have helped to emancipate the incipient domestication processes from the variety of local contexts in which they took place. Since cultivation was part of a network activity taking place in an extended geographical area (and not in a small core region as has been traditionally assumed), migration and exchange among different sedentary communities eventually contributed to a diversification and enrichment of cultivars at any specific location. The resulting recontextualization of cultivation also may have helped to separate wild from cultivated populations, thus contributing to a process by which human-defined plant or animal populations were transformed ultimately into biologically defined populations.

There was, in any case, initially no guarantee that pre-domestication cultivation would necessarily lead to domestication proper. Only at certain points along some trajectories may “tipping points” have been reached that then drove further development in a particular direction, whereas other trajectories may have been aborted or remained in intermediate stages (Fuller, Allaby, and Stevens 2010). Just as with the invention of writing, accidental external circumstances had thus been transformed into conditions for the internal stability and further development of a society.

Ultimately, agricultural economies were established in the Late Pre-Pottery Neolithic that included both livestock and crops. These economies in themselves constituted a successful economic model, which was capable of widespread migration and appropriation.⁸ The transmission of this model must have relied on an action-implicit knowledge system represented by social interactions as well as a material culture comprising agricultural resources and technologies. By carrying seeds and animals into new regions, the “export” of this model may have had yet another recontextualization effect that contributed to its completion and recognition as an autonomous economic system, thus contrasting it with other systems or mixed economies. The expansion and transformation of settlement areas, population growth, as well as further structural changes of societies eventually turned the Neolithic Revolution, like the invention and globalization of writing ultimately based on it, into an irreversible process of global extent.

Neolithic Knowledge Systems

Even without the availability of a written record, some features of the Neolithic knowledge systems still may be recognized from a variety of sources. Sedentariness and cultivation practices favored what one may call a “horizontal organization” of human societies in space and time. This horizontal organization of societies, in the sense of cooperative actions structured by regularities in space and time, preceded the vertical stratification of societies, which was characteristic of the later period of urbanization. Larger settlements capable of food storage emerged whose economic activities were marked by seasonal changes in food supply and the corresponding labor investments. This horizontal organization may well have been what enabled the abandonment of villages at the end of the Pre-Pottery Neolithic B, when people left the foothills for the plains (Asouti 2010, 196).

Early Neolithic settlements must have been precarious institutions in the sense that their sustainability depended not only on a set of environmental factors, but also on labor investments that would not yield immediate benefits. The benefits would be evident only after some time and only if conditions remained stable. Contemporary symbolic practices may have constituted a means to cope with the awareness of this uncertainty and to strengthen social cohesion in such a way as to keep larger communities together. But ritual practices centered on mortuary and perhaps also fertility rituals could also have enabled societies to structure collective actions such as resource scheduling by normative knowledge (Warburton 2004). In any case, the overall result was the emergence of institutionalized cooperative practices that could be structured and optimized around successive steps of labor processes.

It was due to these practices, for instance, that large-scale building projects could be accomplished, far beyond the capacities of individuals or spontaneous collective activities (Kurapkat 2014). In the case of building projects, this capability to conceive and sustain “labor chains” created the conditions for such innovative developments as the invention of bricks, which enabled the separation of the preparation of building materials from the construction process itself. In the case of agriculture, labor chains involving the preparation of soils and the post-processing of crops created a framework for the emergence of domestication. The emergence of agriculture based on domesticated plants depended on the biological adaptation of plants to this new cultural regime, which constituted a niche that had not been originally created to produce this adaptation. The new regime eventually became entrenched in the biological and social conditions of this co-evolutionary process, thus transforming accidental boundary conditions into intrinsic features of the process.

For the evolution of domesticated plants and animals, human labor practices constituted an ecological niche to which they adapted. For the co-evolving human societies, on the other hand, these practices constituted not only a transformation of their environment, but also an external representation of shared knowledge about their interactions with this environment. It could therefore engender thinking processes about how to further change and optimize their living conditions according to their needs. This is why the Neolithic Revolution constitutes not only an economic transformation, or a niche construction in the biological sense, but also a stage in the evolution of knowledge. Furthermore, and coming full circle, the constructed niche of co-evolving humans and their domesticated animals and plants has also left and continues to leave observable changes in our internalized biological “knowledge system,” our genome, whether this is tolerance to lactose, the ability to digest cereals and their fermented products—the beer of Kushim—or dealing with a whole new set of diseases. And, finally, this is why surviving the Anthropocene cannot simply be a matter of economic and technological adjustments, but also depends on whether or not we are capable of taking up the challenges it poses to our knowledge. This is what I believe we can learn from Kushim and his clay tablet.

Acknowledgements

I would like to warmly thank several friends and colleagues for their critical remarks and useful comments on early drafts of this paper. Manfred Laubichler played an important role in the discussions concerning extended evolution, relating cultural and biological evolution. Daniel T. Potts, David A. Warburton, and Svend Hanssen provided valuable criticism and hints concerning the archeological parts, while Robert K. Englund and J. Cale Johnson helped with the emergence of writing. Particular thanks go to Lindy Divarci for her careful editorial work.

References

Footnotes