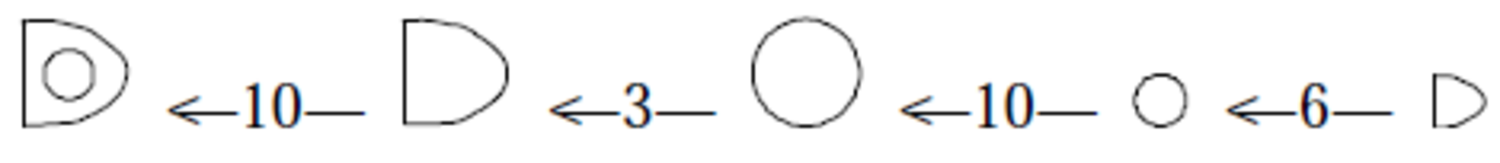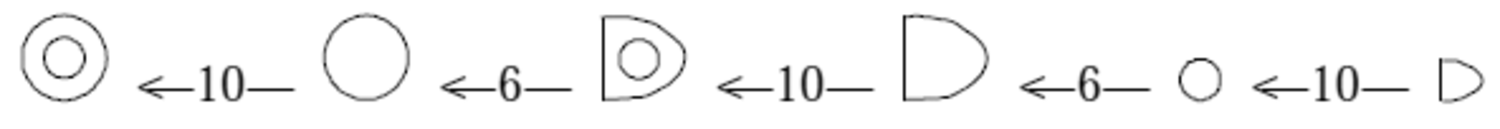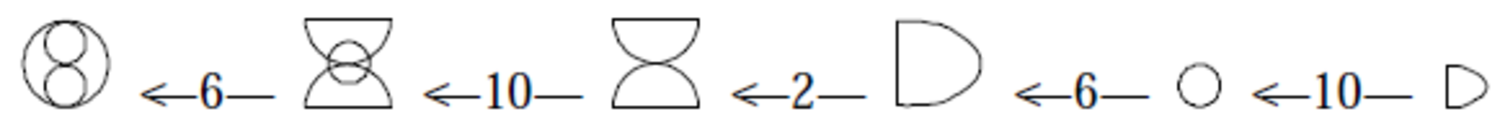3 What Is a Number? What Is a Concept? Who Has a Number Concept?

Peter and I both became interested in Mesopotamian mathematics from debates about the didactics of mathematics, from Piaget, and, of course, from Marx. There were some differences, however. Peter’s Marxism was very Hegelian, while mine was closer to Engels. One evening, about four decades ago, I was on a train in Copenhagen reading Engels’s explanation in the middle of volume 2 of Das Kapital, in which he had been forced to submit arguments from numerical examples to strong editing; in the authorized English translation:

Firmly grounded as Marx was in algebra, he did not get the knack of handling figures, particularly commercial arithmetic, although there exists a thick batch of copybooks containing numerous examples of all kinds of commercial computations which he had solved himself. Marx (1933, 289).¹

I laughed. I suspect that Peter would not have shared my appreciation and would have looked for something deeper in the numerical examples.

The same difference was revealed in our approaches to Piaget. Neither of us fell for Piaget’s infatuation with group “theory” (at least I never heard Peter referring to it, and I certainly did not). But although we were both inspired by Piaget, our thinking about concepts diverged. The concept of “concepts” abounds in Piaget’s work. His title La causalité physique chez l’enfant became The Child’s Conception of Physical Causality in translation (other titles were changed correspondingly), and one volume in the “Jean Piaget Symposium Series” carries the title Conceptual Development: Piaget’s Legacy (Scholnick et al. 1999). Peter maintained in one of our discussions (as I remember it) that inventors and users of protoliterate writing in Uruk in the fourth millennium BCE had no concept of number, firstly because there is no evidence that they mastered an arithmetical structure encompassing addition as well as multiplication (what amounts to practical multiplication may well have been seen as repeated addition),² and secondly because of the way their metro-numerical notations were structured, which I will discuss here (everything, of course, builds on the results obtained by Peter and Robert Englund (1987), with Jöran Friberg in the background).

First, there is the “Še-system,” used for measuring quantities of grain (I leave out the “sub-unit part”):

A couple of variant systems in which small markings are added to the signs were probably used for particular kinds of grain (or for the use of grain in particular processes in so far as this can be distinguished—is malt a different kind of grain or grain used in a particular process?).

Then there is “System S” (“S” for “sexagesimal”), the main number system:

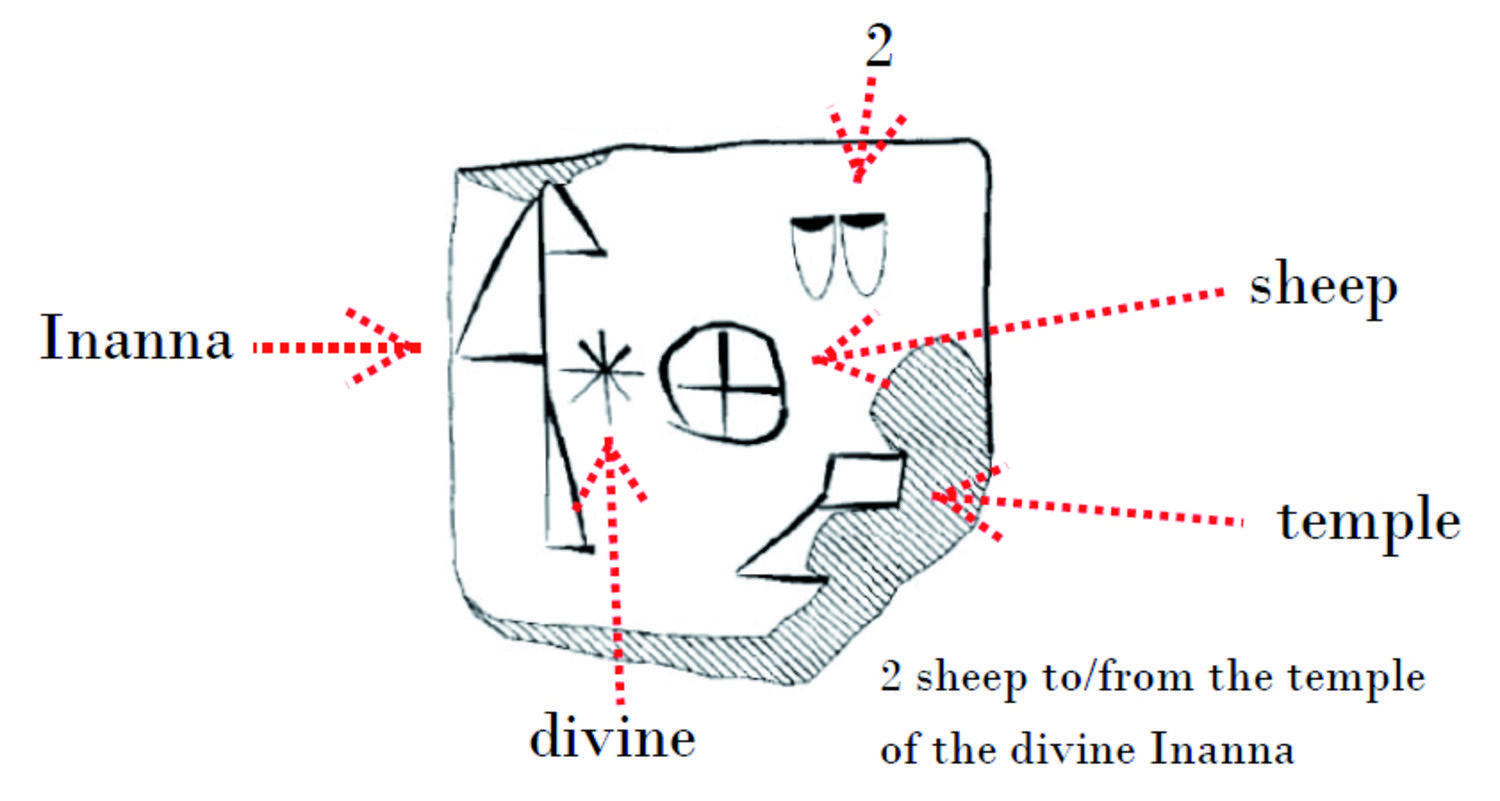
While the Še-system can be used to indicate quantity as well as quality (even though the sign še may be added as a determinative in order to avoid confusion with the same signs used in System S), System S basically designates quantity only, quality being determined separately (“2 sheep”). In this sense, System S is a system used for abstract numbers.

A number sequence with a more restricted use is “System B,” the bisexagesimal system:

Here we see that, until level 60, it coincides with the sexagesimal system. It was apparently used for particular purposes, such as the counting of grain rations, perhaps also of milk products, and possibly, according to one text, fresh fish. A system B* derived from markings is often used without indication of what is being counted—“vermutlich weil das System B* einen so spezifischen Anwendungs­bereich besaß, daß eine nähere qualitative Kennzeichnung des erfaßten Gegenstandes entfallen konnte” (Damerow and Englund 1987, 18).

In spite of this explanation, Peter tended to see the existence of systems like Še and particular counting systems like B as evidence that the protoliterate administrators possessed nothing that he would have accepted as a “number concept.”

As I was also inspired by Piaget, and having made many experiments and observations of my own during the 1970s on the topic, I agreed (and agree) with Peter that speaking of a “number concept” presupposes a certain degree of structure. The intuitive ability to distinguish three items from four without counting may perhaps be seen as an “arithmetical ability,” even though I would hesitate before using this characterization until we have evidence that this ability contributes to the genesis of a genuine number concept. Nor would I speak of a number concept as long as children have learned the number jingle but do not discover a problem when towards the end they “count” in circle, or as long as they have no objections to the “proof” that they have 7 fingers on one hand made by means of a backward step; both change at the time when cardinality and ordinality are merged into a single structure, and when the child knows immediately that there must be more flowers than roses in the garden without wishing to count them.

But my demands for a “number concept” do not go much further. From my experiences with teaching and explaining mathematics I have reached the conviction that concepts are dynamic structures; they grow in fullness as more and more connections are operationally integrated. That is probably also fairly Hegelian (or Hegel on his feet), and probably Peter would not have disagreed if that was what we had discussed. Possibly, our only disagreement was about where to put the lower limit for the number of integrated operations. In any case, this is the reason that I would not take the presence or possible absence of a multiplicative component (distinct from repeated addition) as a yardstick by which the presence or absence of a number concept can be decided, but only as a gauge for the richness of the concept—remembering also that even Euclid’s definition of multiplication (Elements VII, def. 15) refers to repeated addition.

Peter tended to regard the existence of metrological sequences where quantity and quality are merged as a proof that no concept at least of abstract number could be present. On that account I tend to follow Engels, according to whom “100.000 Dampfmaschinen [prove the principle] nicht mehr als Eine” (Engels 1962, 496). I also remember my first physics teacher explaining (I was 11 years old by then) that “density is measured in pure number”; I have no doubt that this teacher possessed a well-developed number concept himself, but he may have found it too difficult for us to understand a ratio g/cm³.³ So, for me “2 sheep” proves that the concept of abstract number was there,⁴ even though its use was no longer compulsory for my physics teacher, as was the explication of the unit once it was decided that densities were being dealt with.

Similarly, I would see the existence of the bisexagesimal system not as proof that the Uruk-IV administrators had no unified number concept but as an early parallel to the particular brick metrologies of the late third millennium, and thus as evidence that they were skillfully adapting their mathematics to the bureaucratic standard procedures of the time.

A final disagreement of ours about number concepts concerned the implications drawn from Igor M. Diakonoff (1983, 88):

The most curious numeral system which I have ever encountered is that of Gilyak, or Nivkhi, a language spoken on the river Amur. Here the forms of the numerals are subdivided into no less than twenty-four classes, thus the numeral ‘2’ is mex (for spears, oars), mik (for arrows, bullets, berries, teeth, fists), meqr (for islands, mountains, houses, pillows), merax (for eyes, hands, buckets, footprints), min (for boots), met’ (for boards, planks), mir (for sledges) etc., etc.

Peter tended to see even this as evidence that no unified number concept was present; I, instead, would observe, as Diakonoff does in the next sentence, that “the root is m(i)- in all cases” and find nothing more than a highly elaborate parallel to the German “ein Mann/eine Frau.” Perhaps we could sum up the whole thing in this way: According to Peter, we should be aware that protoliterate administrators (and so on) did not think in accordance with modern patterns; in my view, even we deviate from these ideologically prescribed patterns much more often than we usually admit. I am not generally a follower of Bruno Latour, but tend to agree that we have never been modern, or at least never as modern as we believe ourselves to be (perhaps interpreting Latour’s phrase in a way that he himself would not accept).

Peter may well have argued that I have misunderstood everything he said (and I, vice versa). This is quite plausible, but this matter of disagreement was never a serious concern for us. We usually discussed our views briefly and then went on to more productive dialogue from which we could learn from each other by sharing information and through mutual critical questioning. That was much more important for both of us, but it is difficult to relate this in an interesting story. In spite of all efforts since Voltaire, war is much more conspicuous in historiography than peace; Voltaire himself had to admit as much in his historical writings.

References

Footnotes