Introduction
On various occasions, Piaget reminisced that it was Einstein who inspired him to study the genesis of temporal concepts.1 The foreword to his 1946 study on “the child’s conception of time”2 begins like this:
This work was prompted by a number of questions kindly suggested by Albert Einstein more than fifteen years ago, when he presided over the first international course of lectures on philosophy and psychology at Davos. (Piaget 1969, ix)
Unfortunately, we do not have independent documentation of Einstein’s suggestions. But Piaget continues to specify the proposed research with the following questions:
Is our intuitive grasp of time primitive or derived? Is it identical with our intuitive grasp of velocity? What if any bearing do these questions have on the genesis and development of the child’s conception of time? (Piaget 1969, ix)
Piaget goes on to tell us that after Einstein’s inspiring question, every year he devoted some investigation to these issues although initially he had no hope of finding anything out since the “time relationships constructed by young children are so largely based on what they hear from adults and not on their own experiences.” It was only after his investigations on the child’s conceptions of number and quantity that he found a way to disentangle the various aspects of the concept of time and to dissociate its specific content from the notions of space and motion.
In Peter Damerow’s and Wolfgang Lefèvre’s research colloquium on “problems of conceptual development in the history of the natural sciences,” we studied Piaget’s work for several months in the fall of 1985. We read, in particular, his investigations on the genetic conception of time. Peter criticized Piaget’s “concept of reflective abstraction” because of its implication that “the material means of the actions on which cognitive activity is based are irrelevant for the development of cognitive abilities” (Damerow 1996, 9). Nevertheless, Peter tried to convince us that Piaget’s analysis of the concept of time carries significance and also provides insight for a historiography of temporal concepts. Those discussions with Peter proved to be some of the formative moments in my intellectual biography. In this contribution, I want to take a look again at Piaget’s analysis of the concept of time and make a few comments on the question as to how his analysis may carry over to the conceptual context of the special theory of relativity.
Piaget’s Analysis of Classical Temporal Concepts
The core of Piaget’s investigation is one particular experiment, which I will discuss in more detail below. It was designed against the background of Piaget’s tenet of the specific characteristic of the concept of time. To begin with, Piaget pointed out that temporal judgments are actually not distinct from spatial judgments, as long as only one kind of motion is considered. In various experiments, Piaget demonstrated that correspondingly, with young children of the pre-operational stage, temporal judgments of ‘earlier’ and ‘later,’ or comparisons of time spans as ‘shorter’ and ‘longer,’ are based only on spatial seriation. An object moving from left to right is first at point A and then at point B if and only if A is left of B. Similarly, the time a body needs to go from point A to B is longer than the time it needs to go from C to D if and only if the distance between A and B is larger than the distance between C and D. Children will find out that things get more complicated if non-uniform motion is involved, but structurally temporal concepts are not distinguished from spatial concepts as long as only one kind of independent motion is considered.
When two different motions have to be compared, the initial reliance on basing temporal judgments on spatial features perseveres. There is a correspondence here between the child’s concept of speed and the Aristotelian concept of velocity as the finite distance traversed in a finite amount of time. Judgments of comparison between different velocities are based on various proportionalities that follow from the Aristotelian concept. One body moves faster than another one if it traverses a longer distance in the same amount of time. It is also faster if it traverses the same distance in a smaller amount of time. A composition of both proportionalities can lead to contradictions if the conditions of equal time or equal distance are violated. Thus, if two bodies start moving at the same time from point A and one body arrives at B a little later than the other body arrives at C, but B is farther away from A than C, the first body is either moving faster since it traverses a larger distance or slower since it arrives later at its terminal point.
It is only when different motions have to be judged which are largely causally independent but have to be coordinated at specific points of simultaneity that the specific concept of time needs to be invoked. In order to demonstrate that it is this coordination of different motions that constitutes the conception of time and to isolate its specific deductive capacity, Piaget devised his experiment (see fig. 11.1).
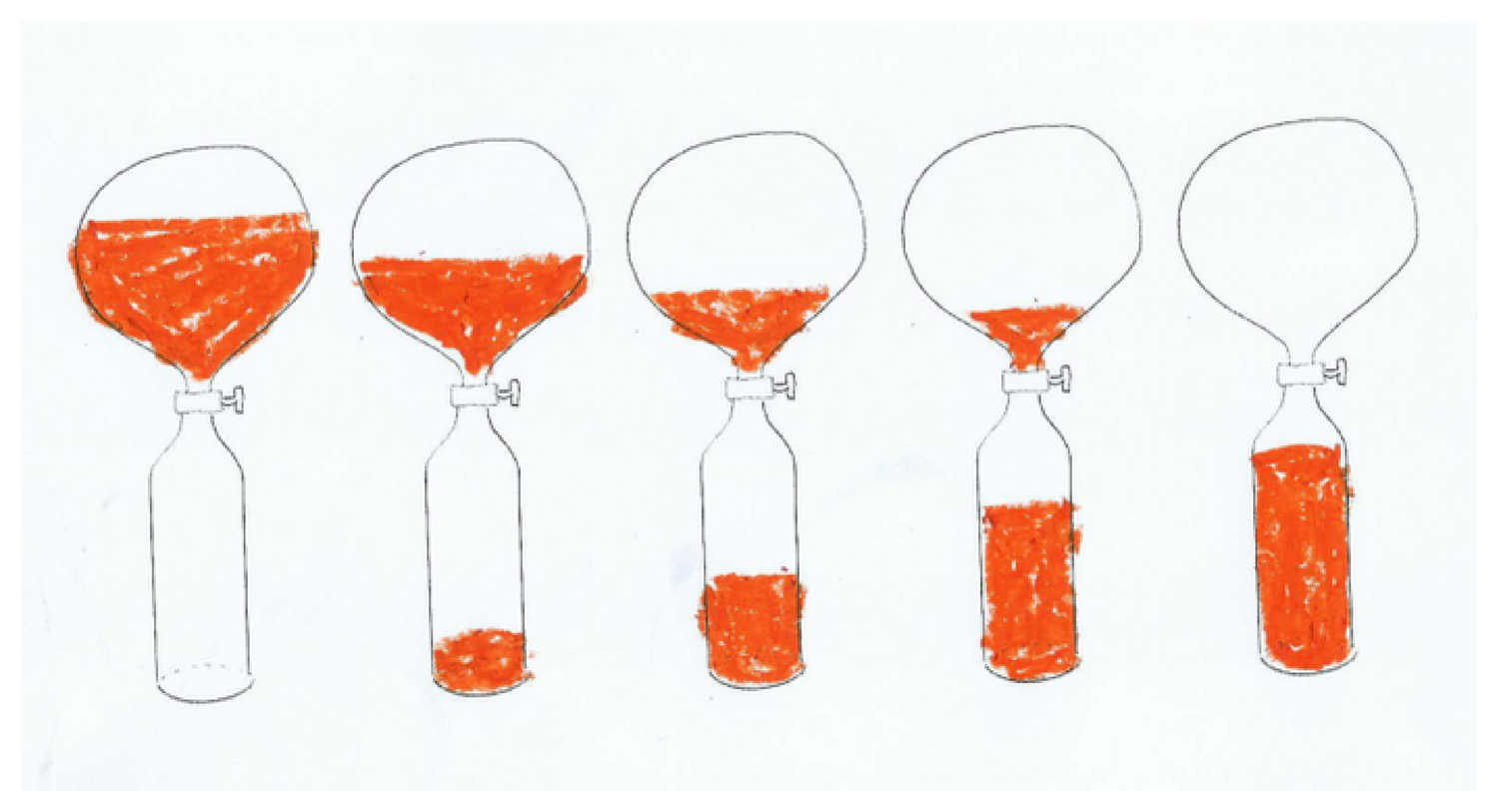
Fig. 11.1: In one of his experiments reported in Piaget (1946), a colored liquid is flowing from one bottle into another one through a valve. Children are shown the process and asked to mark successive water levels on prepared sheets of paper. They are then asked to reconstruct the sequence of sketches after the individual sheets were cut in half along the valve.
Two bottle-like vessels of different shape, one pear-shaped, the other of cylindrical form, are connected in such a way that a colored liquid would flow downwards from one bottle into the other through a valve that could be opened and closed. The experimenter would then let children observe a demonstration where the entire liquid is initially in the upper vessel and then is allowed to flow down into the lower vessel in certain discrete amounts. The children would get a number of prepared papers showing the two empty vessels and were asked to draw the water levels in each vessel onto their papers at each stage of the process. Thus, at the conclusion of the demonstration, when the liquid was entirely contained in the lower vessel, the children had created a series of half a dozen or so drawings of the two bottles with different water levels in each. The drawings were then shuffled and the children were asked to put them back into order again according to a temporal sequence. In a second part of the experiment, the drawings were then cut in the middle in such a way that the two halves would show the upper or the lower vessel, respectively. Again, the drawings were shuffled, and the children were asked to reconstruct the original sequence.
Piaget’s observation was that very young children were not able to reconstruct the original sequence at all, even in the first part of the experiment with the intact drawings. Older children were able to put the uncut drawings in the correct sequence but failed to reconstruct the correct sequence when the drawings had been cut apart. Typically, what would happen is that random pairs of images of the upper bottle and images of the lower bottle would be formed and children at this stage would construct a sequence based on either the lower half or the upper part but with the randomly formed pairs kept intact. Thus, the water level in the reconstructed sequence would correctly rise in the lower vessel but the upper portion would show a random or wrong sequence, or vice versa. Only at the final stage were the children able to break up pairs at will and construct two coordinated sequences of rising water level in the lower bottle and sinking water level in the upper bottle, put together in such a way that the lowest level in the lower bottle would correspond to the highest level in the upper bottle.
Several features of Piaget’s experiment are worth pointing out. First, it does not matter how much time actually passes during the experiment. Since the valve is opened and closed by the experimenter at will, more or less physical time passes between subsequent stages of the experiment. The experiment thus exemplifies Piaget’s conviction that time is a cognitive construct, a deductive scheme, not an intuition or form of sensibility. Second, the ability to reconstruct the correct sequence of images depends crucially on the mental ability to reverse and to anticipate the actual physical process. Whereas the actual flow of time and the causal processes are irreversible, the conception of time is dependent on the mental capacity to reverse, anticipate, and interpolate causal processes. In a process of decentration, children construct a uniform, homogeneous time that allows a coordination of different sequences of events.
Piaget captured his understanding of the concept of time as a co-seriation of different sequences of physical events in an intuitive graphical representation (see fig. 11.2).
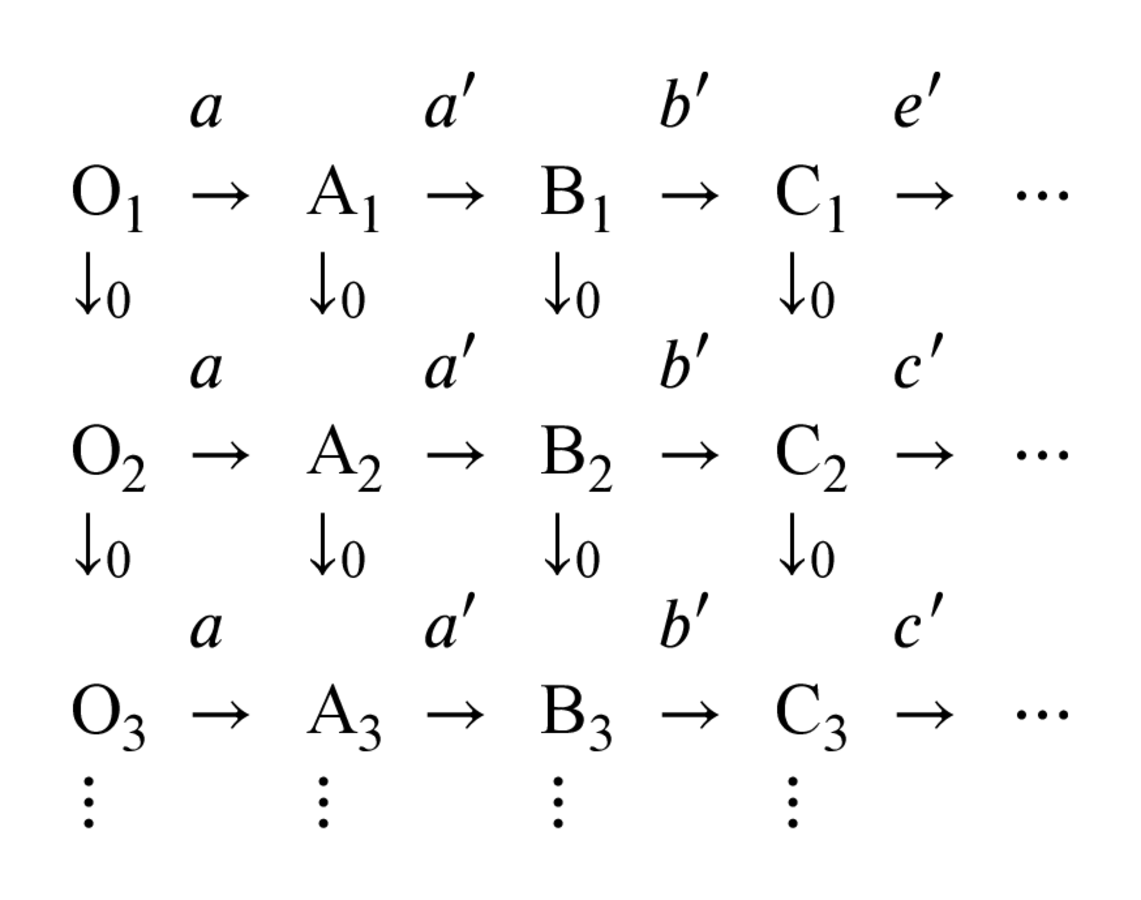
Fig. 11.2: Piaget’s graphical illustration of his concept of co-seriation (Piaget 1969, 264).
A sequence of events, or a motion, is characterized by points
 ,
,
 , etc. that follow each other in a relation of earlier and later in some causally determined way. They are coordinated with other sequences of events, or motions,
, etc. that follow each other in a relation of earlier and later in some causally determined way. They are coordinated with other sequences of events, or motions,
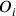 ,
,
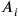 , etc. such that
, etc. such that
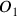 ,
,
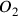 ,
,
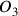 , etc. are put into a relation of simultaneity. Uniform time is not bound to any one specific sequence of events or motion but rather arises from the coordinating operations as a cognitive construction that allows the co-seriation of the different sequences of events
, etc. are put into a relation of simultaneity. Uniform time is not bound to any one specific sequence of events or motion but rather arises from the coordinating operations as a cognitive construction that allows the co-seriation of the different sequences of events
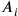 ,
,
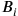 , etc. and the different time spans
, etc. and the different time spans
 ,
,
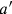 ,
,
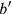 , etc.
, etc.
Piaget on the Concept of Time in Relativity
Piaget’s concept of time as a cognitive ability of co-seriation is a convincing analysis of the concept of “absolute time” in classical mechanics. Its genesis in the development of children illustrates Piaget’s idea that cognitive development proceeds along stages of ever more far-reaching decentration, which in turn result from ever-increasing capacities of transformational operations. In his 1946 book, Piaget concluded his analysis with a perspective on the question of how his analysis would carry over to the problem of understanding time in the special theory of relativity.
It remains frustratingly unclear how Piaget would have applied his analysis to the genetic explanation of special relativity. In fact, the few remarks that he gives in his 1946 book are altogether too vague to allow us even to assess whether Piaget fully understood the difference between temporal conceptions implied by the special theory of relativity and those of classical Newtonian mechanics.
In special relativity, there is no universal time. But Piaget, when he talks about Kant, says:
As Kant has shown so clearly, time and space are not concepts but unique ‘schemes’—there is only one time and one space in the entire universe. (Piaget 1969, 33)
Are we supposed to read the assertion of the unique existence of one and only one universal time as restricted to Kant, or would Piaget approve of this assertion in general? At other places, he talks about the ‘relative time’ (p. 396) but also about the ‘time of relativity theory.’ Indeed, the final passages of the book pertain explicitly to the theory of special relativity and show the same ambivalence and ambiguity. Piaget wrote:
As for the time of relativity theory, far from being an exception to this general rule, it involves the co-ordination of motions and their velocities even more clearly than the rest. (Piaget 1969, 278f)
So far, so good, and one would be tempted to agree with Piaget on this general level, if suspicions would not have been raised by the unqualified use of the term ‘time of relativity theory.’ In relativity theory, there is no such thing as ‘the time,’ but, of course, Piaget could have meant the ‘concept of time’ in relativity theory. But what follows immediately afterwards carries the same ambivalence. He goes on to say:
Let us recall first of all that relativity theory never reverses the order of events in terms of the observer’s viewpoint: ifprecedes
when considered from a certain point of view, it can never follow
when considered from a different standpoint, but will at most be simultaneous with it. (Piaget 1969, 279)3
How should we interpret Piaget here? Apparently
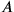 and
and
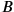 would be two events. Let’s coordinatize them in some frame of reference,
would be two events. Let’s coordinatize them in some frame of reference,
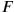 as
as
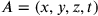 and
and
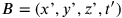 (see fig. 11.3). Here
(see fig. 11.3). Here
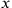 ,
,
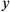 ,
,
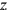 , and
, and
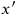 ,
,
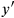 ,
,
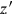 denote spatial coordinates,
denote spatial coordinates,
 and
and
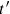 denote the time coordinate (in the following, we will suppress the irrelevant
denote the time coordinate (in the following, we will suppress the irrelevant
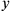 - and
- and
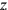 -coordinates). To say that
-coordinates). To say that
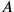 happens before
happens before
 , would then mean that
, would then mean that
 or
or
 .
.
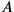 and
and
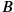 in a spacetime diagram. In the red (dashed) coordinate system
in a spacetime diagram. In the red (dashed) coordinate system
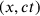 , horizontal lines parallel to the
, horizontal lines parallel to the
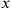 -axis represent (hyper)surfaces of simultaneous events, and in these coordinates
-axis represent (hyper)surfaces of simultaneous events, and in these coordinates
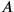 precedes
precedes
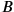 . But for an observer moving rapidly along the
. But for an observer moving rapidly along the
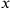 -direction, the blue (dotted) coordinate system
-direction, the blue (dotted) coordinate system
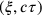 is used and the tilted lines parallel to the
is used and the tilted lines parallel to the
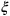 -axis represent (hyper)surfaces of simultaneous events. In the blue (dotted) frame of reference, the event B precedes A. However, for events
-axis represent (hyper)surfaces of simultaneous events. In the blue (dotted) frame of reference, the event B precedes A. However, for events
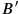 in the timelike future of
in the timelike future of
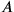 , the event
, the event
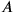 precedes
precedes
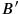 in all possible frames of reference.
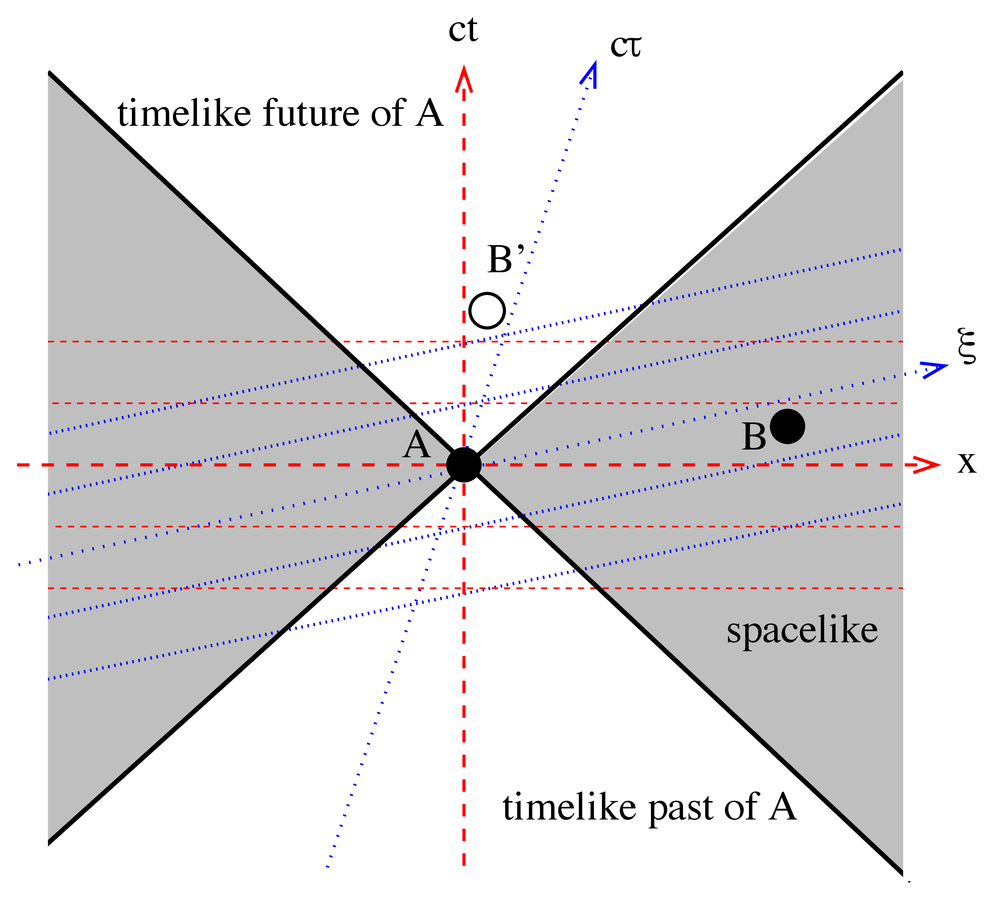
in all possible frames of reference.Fig. 11.3: Illustration of the relativity of simultaneity of two spacelike separated events
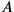 and
and
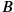 in a spacetime diagram. In the red (dashed) coordinate system
in a spacetime diagram. In the red (dashed) coordinate system
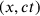 , horizontal lines parallel to the
, horizontal lines parallel to the
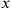 -axis represent (hyper)surfaces of simultaneous events, and in these coordinates
-axis represent (hyper)surfaces of simultaneous events, and in these coordinates
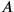 precedes
precedes
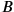 . But for an observer moving rapidly along the
. But for an observer moving rapidly along the
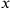 -direction, the blue (dotted) coordinate system
-direction, the blue (dotted) coordinate system
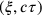 is used and the tilted lines parallel to the
is used and the tilted lines parallel to the
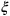 -axis represent (hyper)surfaces of simultaneous events. In the blue (dotted) frame of reference, the event B precedes A. However, for events
-axis represent (hyper)surfaces of simultaneous events. In the blue (dotted) frame of reference, the event B precedes A. However, for events
 in the timelike future of
in the timelike future of
 , the event
, the event
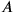 precedes
precedes
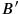 in all possible frames of reference.
in all possible frames of reference.
In fig. 11.3, horizontal red (dashed) lines denote events with the same
 or
or
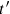 , respectively, that is, events on the same horizontal red (dashed) line are simultaneous in
, respectively, that is, events on the same horizontal red (dashed) line are simultaneous in
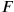 . Clearly, with respect to the red (dashed) lines of simultaneity,
. Clearly, with respect to the red (dashed) lines of simultaneity,
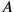 precedes
precedes
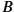 . Now let’s look at the two events from a frame of reference
. Now let’s look at the two events from a frame of reference
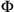 moving with respect to
moving with respect to
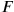 with velocity
with velocity
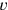 along the
along the
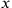 -direction. In
-direction. In
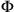 , we have
, we have
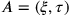 and
and
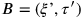 , and in
, and in
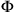 the temporal difference between the two events is
the temporal difference between the two events is
 . But if we interpret Piaget’s phrase ‘from a certain point of view’ as ‘in a certain frame of reference,’ his claim is wrong. To see this, consider the Lorentz transformations that allow us to go from
. But if we interpret Piaget’s phrase ‘from a certain point of view’ as ‘in a certain frame of reference,’ his claim is wrong. To see this, consider the Lorentz transformations that allow us to go from
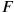 to
to
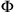 :
:
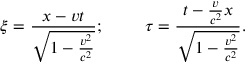
|
11.1 |
We then get
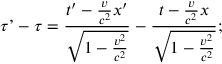
|
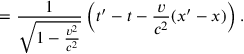
|
11.2 |
Clearly, we can have
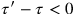 or
or
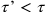 , that is, a reversal in the temporal order of the two events in
, that is, a reversal in the temporal order of the two events in
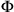 , if
, if
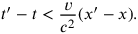
|
11.3 |
In fig. 11.3, blue (dotted) lines parallel to the
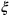 -axis denote events with the same
-axis denote events with the same
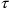 or
or
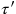 , respectively, that is, events on the same (tilted) blue (dotted) line are simultaneous in
, respectively, that is, events on the same (tilted) blue (dotted) line are simultaneous in
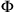 . One sees that, with respect to the blue (dotted) lines of simultaneity,
. One sees that, with respect to the blue (dotted) lines of simultaneity,
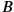 precedes
precedes
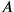 .
.
That is to say, if the two events
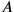 and
and
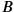 are sufficiently far away from each other spatially in
are sufficiently far away from each other spatially in
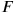 , then an observer dashing by along their line of connection with a speed
, then an observer dashing by along their line of connection with a speed
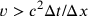 would see the two events in reverse order. And if
would see the two events in reverse order. And if
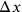 , the spatial distance of
, the spatial distance of
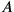 and
and
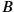 as measured in
as measured in
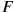 , is sufficiently large, there will be no problem in satisfying that condition. What we have shown is simply the well-known tenet that for any two events
, is sufficiently large, there will be no problem in satisfying that condition. What we have shown is simply the well-known tenet that for any two events
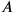 and
and
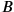 whose separation is spacelike (the shaded region in fig. 11.3), that is, for which
whose separation is spacelike (the shaded region in fig. 11.3), that is, for which
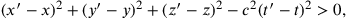
|
11.4 |
the temporal order is undefined and depends on the state of motion of the observer.
Piaget’s formulation is vague enough to allow for different, and correct, interpretations. After all, we are talking only about the final paragraph of an entire book. He could have meant two events happening along the world line of a material particle, or in other words, he could have meant that two events might be causally connectable in the sense that their separation is timelike.
In fact, it seems that we may indeed have been too critical in our reading of the above passage. Four years later, Piaget incorporated the results of his 1946 book on the genesis of the conception of time into his 1950 Introduction à l’Épistémologie Génétique, in its second volume dealing with La Pensée Physique. There, we find the same statement again in paragraph V of chapter IV, section 3, entitled “The relativistic metric.”
In this paragraph, Piaget first claims quite generally that his analysis of the (classical) conception of (absolute) time as supervenient on the concept of velocity suggests the naturalness of the relativity revolution. That is because “[...] all modifications of our ideas about velocity imply a transformation of our conception of time.”4 Since in the development of physics, the velocity of light had emerged as a limiting speed that cannot be surpassed by the propagation of any causally efficacious signal, it followed with necessity that both the concept of velocity and the notion of time were subject to joint modification according to the genetic viewpoint:
As soon as Michelson’s and Morley’s measurements had verified the special character of the speed of light and its complete isotropy, the genetic conception, which connects the idea of time with that of velocity, required a simultaneous modification of these two concepts. This revision of the physical concepts as a function of ideas about time and velocity was carried out by Einstein with well-known success. (Piaget 1950, 45)
The modification required by the axiom of the limiting value of the speed of light pertains immediately to the concept of simultaneity. If there is a maximal limit velocity, it follows that the simultaneity of distant events is no longer absolute but relative to the velocity of an observer, just as children will deny that two lights are switched on simultaneously if the lights are some meters apart and the children cannot see them at the same time (Piaget 1969, 110–115). It is only for spatially neighboring events that a concept of simultaneity survives, and it is here that we find the incriminating sentence again, embedded in a context which makes it clear that Piaget is thinking about “neighboring events,” that is, events which are spatially close together.
Since the simultaneity of events at neighboring [my emphasis, TS] places [...] is not changed, the same is true for the temporal sequence. (Piaget 1950, 47)
The sentence about the invariance of temporal sequence which we criticized above follows immediately after this qualification.
Nevertheless, Piaget offers us only analogies when it comes to the genetic explanation of relativity:
On the other hand, this concept of relativity of duration requires an effort of coordination in order to equilibrate the viewpoints of observers moving with different velocities. This effort is only a continuation of the effort of coordination that the child has to master in order to comprehend the heterogenous durations, which it associates with different velocities, in terms of a unique common time. As paradoxical as it may seem, the relative durations and the proper times of Einstein’s theory relate to absolute time as absolute time to the individual times and local times of the child’s intuition. (Piaget 1950, 46)
That is to say, the coordination efforts that give rise to the child’s forming a unique common time are analogous to the coordination efforts that a classically trained physicist has to master in order to overcome the limitations of the absolute time of Newtonian mechanics. But what Piaget calls paradoxical here is perhaps only a consequence, as we will see below, of the lack of a proper term that would identify the genetic analog of absolute time in a relativistic context.
In any case, Piaget puts the coordination of different velocities that underlies the genesis of the concept of absolute time in perfect parallel to the coordination of velocities that underlies the genesis of relativistic concepts:
In both cases, time appears as a coordination of velocities, and the transition from velocities that cannot be coordinated to those that can be coordinated, which is made possible by means of a homogeneous and uniform time, is a first stage of transformation from an erroneous egocentric absoluteness into objective relations. A second stage makes possible the transition from absolute time (and the possibility of an infinite velocity) to relative time, which is connected with a precise coordination of velocities. (Piaget 1950, 46)
Einstein and the Special Theory of Relativity
As far as it goes, Piaget’s interpretation of the genetic basis of special relativity provides an interesting perspective. But as it stands it is a mere program or an abstract conceptual framework. It needs to be spelled out. Here I want to make only a few comments.
I want to look at the locus classicus for the emergence of the special theory of relativity, Einstein’s paper on the “Electrodynamics of Moving Bodies” (1905). What are the analogues of the experiences and efforts of coordination that underlie the emergence of relativistic temporal and spatial concepts? To what extent are those experiences and coordination efforts comparable to the ones that the child is confronted with and needs to master, and where are they different? Does the difference in the experiential foundation of special relativity have implications for the character of temporal concepts in the relativistic context?
The first observation we might make is that we can read the entire § 1 of “Electrodynamics of Moving Bodies” as an elaboration of the classical, Newtonian time concept along the lines of Piaget’s analysis. Just in passing we may remark that the very term “coordinate system” indicates the very coordination efforts that may be interpreted in Piagetian terms. In § 1 Einstein expounds the problems of the concept of distant simultaneity and defines a global time in an inertial frame of reference by a system of clocks that are located everywhere in space and coordinated by the exchange of light signals. This system of clocks is the idealized materialization of the uniform time that allows an operational coordination of different motions, but only within the same inertial frame. As Einstein concludes: “It is essential that we have defined time by means of clocks at rest in a system at rest; because it belongs to the system at rest, we designate the time just defined as ‘the time of the system at rest.’” (Einstein 1905, 894f).
It is only in the following sections that Einstein addresses the crucial question of coordinating the experiences of two observers who are in a state of uniform relative motion with each other. Very explicitly in § 2, Einstein constructs a situation where the observer dependence of spatio-temporal judgments becomes obvious. He looks at the task of determining the length of a moving rigid rod from the point of view of two observers. One observer is co-moving with the rod. In his inertial system the rod is at rest and its length can be determined by physical comparison with another rod that serves as an etalon. The other observer determines the length of the moving rod from a coordinate system at rest by looking at which points in space the end points of the rod are located at some point
 of time in his coordinate system. While “the commonly used kinematics tacitly assumes that the lengths determined by the two methods are exactly identical” (Einstein 1905, 894f), Einstein finds that they are, in fact, not the same. This result raises the problem of how one can go back and forth from one frame of reference to another one that is moving with respect to the first.
of time in his coordinate system. While “the commonly used kinematics tacitly assumes that the lengths determined by the two methods are exactly identical” (Einstein 1905, 894f), Einstein finds that they are, in fact, not the same. This result raises the problem of how one can go back and forth from one frame of reference to another one that is moving with respect to the first.
This coordination task of operationally moving between different frames of reference is solved by finding coordinate transformations between the (orthogonal Cartesian) coordinates
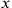 ,
,
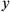 ,
,
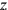 ,
,
 of a frame of reference
of a frame of reference
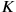 , and the coordinates
, and the coordinates
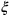 ,
,
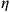 ,
,
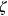 ,
,
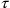 of a system
of a system
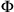 . The transformations that mediate between the two systems of coordinates are the Lorentz transformations (11.1). Their form and some of their properties were known to Einstein before, but the essential core and content of his 1905 paper is to show how the Lorentz transformations are justified and how they actually work in mediating the operational coordination between moving frames of reference.
. The transformations that mediate between the two systems of coordinates are the Lorentz transformations (11.1). Their form and some of their properties were known to Einstein before, but the essential core and content of his 1905 paper is to show how the Lorentz transformations are justified and how they actually work in mediating the operational coordination between moving frames of reference.
In the “kinematical part,” Einstein derives the Lorentz transformations from the two basic principles, the principle of relativity and the speed of light postulate, and he shows that they are compatible with the assumption that all moving observers measure the same vacuum speed of light. They also imply the relativity of simultaneity for observers in relative motion as well as length contraction and time dilation. He also looks at the addition of velocities and finds that the classical law of addition of velocities is modified by the Lorentz transformations to a new law, and one of its implications is that by composition of velocities one can never exceed the velocity of light.
In the “electrodynamic part,” Einstein addresses the question as to how electrodynamical processes are to be transformed if viewed from different frames of references. Technically, the core result is the transformation law for the electric and magnetic fields. It is here that the capacity of transforming back and forth between moving frames of reference becomes fully operational. Einstein shows that in all frames of reference, the Maxwell equations for the electromagnetic field in a vacuum hold if the fields are properly transformed. He looks at specific problems from the point of view of different observers and explicitly performs the necessary transformational operations. One such problem is the shape of a moving electron, which is assumed to be a rigid sphere in a frame of reference in which it is at rest, and the related problem of transforming the equations of motion of a moving charge. Another such problem is the investigation of the relativistic Doppler effect by asking how a light source would appear to an observer who is rapidly moving toward it.
All this is well-known, but it illustrates the main point one might want to make from a genetic perspective. The relativistic concepts arise from a technical competence of actively changing perspectives by reversible, operational transformations between the viewpoints of moving observers. But the decentration that results from those efforts is of a special kind, which is responsible for the notorious difficulty of learning and teaching relativity theory. The change of perspective between frames of references that is relevant here is almost never—certainly not to Einstein—one that is subject to human experience. To be sure, the empirical consequences of relativity theory have amply been confirmed and even play a role in today’s practical life. Nevertheless, the operational transformations that mediate between different frames of reference, to the extent that relativistic implications become important, are entirely theoretical. They are mental operations making use of conceptual and calculational means of deduction. They arise from technical operations that are connected with the manipulation of coordinate systems and coordinate transformations as well as their imagined interpretations. Humans are terrestrial observers moving slowly about the surface of the earth. The laws of physics as they would appear to an observer who is co-moving with a fast moving electron, or a canal ray or an astrophysical object, are not subject to any direct experiential concretization. Nor can we experience how a light source would look if approached with close to luminal velocities. The change of perspective and the cognitive effort of coordinating causal processes viewed from different frames of reference are mental operations mediated through specific mathematical representation.
On the other hand, the relevant transformations have to be carried out in an exact and quantitative way. The results carry empirical significance and could be confronted with observation and this is what eventually made the cognitive restructuring inevitable. For Einstein, the relevant experimental context of the early twentieth century involved the investigation of the dynamics of beta and cathode rays, that is, of fast moving electrons, as well as experiments, such as Fizeau’s or Michelson’s, of measuring the velocity of light, and astronomical effects like stellar aberration.
Another difficulty of transferring Piaget’s analysis of pre-classical and Newtonian temporal concepts to the conceptual context of special relativity seems to be implied by the use of phrases like “time of relativity” or “relativistic time.” If the classical conception of time emerges from the operational co-ordination of co-displacements or from the co-seriation of causal sequences of events, then the analog of classical time in the relativistic context should no longer be called “time.” What emerges from the efforts of co-ordination of physical processes between frames of references moving relative to each other with velocities comparable to the limit speed of light is not a new concept of time. It is a new conception and conceptual framework of spatio-temporal relations that is best captured by a term that was not available to Einstein in 1905. An appropriate term only emerged a few years later with Hermann Minkowski’s reinterpretation of relativistic concepts in terms of a four-dimensional “world” in which spatial and temporal relations are only projections of every individual observer, or in Minkowski’s oft-quoted words:
The views on space and time which I wish to lay before you have sprung from the soil of experimental physics. Therein lies their strength. Their tendency is radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality. (Minkowski 1909, xiv)
Minowski’s “world” is nowadays called Minkowski spacetime, a four-dimensional Riemannian manifold with a Minkowski metric. In Minkowski spacetime any relative times and spaces appear as projections relative to an observer, as was illustrated graphically in fig. 11.3. It is Minkowski spacetime—the entire spatiotemporal structure, not any ‘relative time’ or ‘time of relativity theory’—which constitutes the invariant entity emerging from the coordination efforts and allowing for the transformational operations of going back and forth at will between the possible experiences of different inertial observers.
Acknowledgments
I wish to thank Katja Bödeker, Thomas Kesselring, Tim Räz, and Andreas Verdun for comments on an earlier version of this paper.
References
Damerow, Peter (1996). Prehistory and Cognitive Development: Invited Lecture at the Twenty-Fifth Annual Symposium of the Jean Piaget Society Berkeley, June 1 – June 3, 1995. Preprint 30. Berlin: Max Planck Institute for the History of Science.
Einstein, Albert (1905). Zur Elektrodynamik bewegter Körper. Annalen der Physik 17. Reprinted in The Collected Papers of Albert Einstein. Vol. 2. The Swiss Years: Writings, 1900–1909. Princeton: Princeton University Press, 1989, pp. 276–310.:891–921.
Minkowski, Hermann (1909). Raum und Zeit. Physikalische Zeitschrift 10(104–111). Reprinted and translated in Minkowski Spacetime: A Hundred Years Later, Vesselin Petkov, ed. Dordrecht: Springer 2010, pp. xiv–xlii.
Piaget, Jean (1946). Le Developpement de la Notion de Temps chez l’Enfant. Paris: Presses Universitaires de France.
– (1950). Introduction a l’Épistémologie Génétique. Tome II: La Pensee Physique. Paris: Presses Universitaires de France.
– (1957). The Child and Modern Physics. Scientific American 196(3):46–51.
– (1969). The Child’s Conception of Time. English translation of Piaget (1946). New York: Basic Books.
Footnotes
The vagueness is not an artifact of the translation; in the original French, the passage reads: “Rappelons d’abord que, en aucun cas, il n’aboutit à inverser l’ordre des phénomènes en fonction des points des vue: si A est antérieur à B, d’un certain point de vue, il ne sera jamais ultérieur à B, d’un autre point de vue, mais tout au plus simultané.” (Piaget 1946, 298).
