We still have not decided what is to be meant by “algebra.”
Be that as it may, all problems dealt with in Chapters 2–4 can be translated into modern algebraic symbols (albeit with a certain loss of information). On the whole the same can be said about the methods used to resolve them.
Such a translation will not be possible in the problems that are analyzed in the present chapter. There is, however, a fairly close connection between the methods that are applied here and those which we know from the preceding chapters. In this sense at least it seems legitimate to speak of them as “quasi-algebraic.”
VAT 8512
Obv.
1A triangle. 30 the width. In the inside two plots,
2the upper surface over the lower surface, 7‵ went beyond.
3The lower descendant over the upper descendant, 20 went beyond.
4The descendants and the bar what?
5And the surfaces of the two plots what?
6You, 30 the width posit, 7‵ which the upper surface over the lower surface went beyond posit,
7and 20 which the lower descendant over the upper descendant went beyond posit.
8igi 20 which the lower descendant over the upper descendant went beyond
9detach: 3′ to 7‵ which the upper surface over the lower surface went beyond
10raise, 21 may your head hold!
1121 to 30 the width join: 51
12together with 51 make hold: 43‵21
1321 which your head holds together with 21
14make hold: 7‵21 to 43‵21 join: 50‵42.
1550‵42 to two break: 25‵21.
16The equal of 25‵21 what? 39.
17From 39, 21 the made-hold tear out, 18.
1818 which you have left is the bar.
19Well, if 18 is the bar,
20the descendants and the surfaces of the two plots what?
21You, 21 which together with itself you have made hold, from 51
22tear out: 30 you leave. 30 which you have left
23to two break, 15 to 30 which you have left raise,
247‵30 may your head hold!
Edge
118 the bar together with 18 make hold:
25‵24 from 7‵30 which your head holds
3tear out: 2‵6 you leave.
Rev.
1What to 2‵6 may I posit
2which 7‵ which the upper surface over the lower surface went beyond gives me?
33°20′ posit. 3°20′ to 2‵6 raise, 7‵ it gives you.
430 the width over 18 the bar what goes beyond? 12 it goes beyond.
512 to 3°20′ which you have posited raise, 40.
640 the upper descendant.
7Well, if 40 is the upper descendant,
8the upper surface is what? You, 30 the width,
918 the bar heap: 48 to two break: 24.
1024 to 40 the upper descendant raise, 16‵.
1116‵ the upper surface. Well, if 16‵ the upper surface,
12the lower descendant and the lower surface what?
13You, 40 the upper descendant to 20 which the lower descendant over the upper descendant goes beyond
14join, 1‵ the lower descendant.
1518 the bar to two break: 9
16to 1‵ the lower descendant raise, 9‵.
179‵ the lower surface.
Many Old Babylonian mathematical problems deal with the partition of fields. The mathematical substance may vary—sometimes the shape of the field is irrelevant and only the area is given together with the specific conditions for its division; sometimes, as here, what is asked for is a division of a particular geometric shape.
Already before 2200 bce, Mesopotamian surveyors knew how to divide a trapezium into two equal parts by means of a parallel transversal; we shall return in a short while to how they did it. A similar division of a triangle cannot be made exactly without the use of irrational numbers—which means that it could not be done by the Old Babylonian calculators (except with approximation, which was not among the normal teaching aims).
The present problem deals with a variant of the triangle division which can be performed exactly. As we see in lines Obv. 1–3 and as shown in Figure 5.1, a triangular field is divided into two parcels (an “upper surface” and a “lower surface”) by a “bar,” that is, a parallel transversal. For simplicity we may assume the triangle to be rectangular. It is almost certain that the author of the text did as much, and that the “descendants” are thus part of the side; but if we interpret the “descendants” as heights, the calculations are valid for an oblique triangle too.
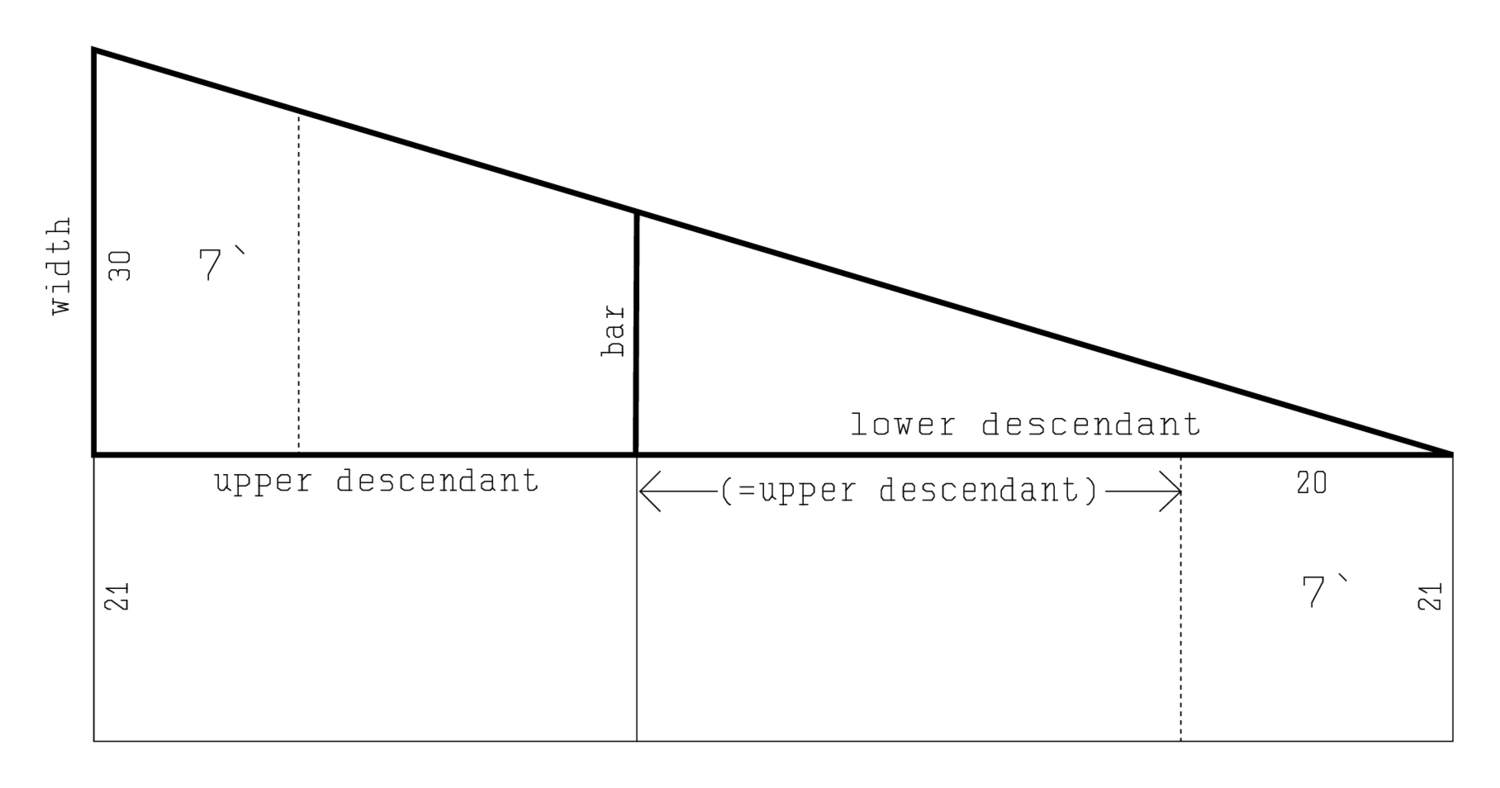
Fig. 5.1: The triangular divided field of VAT 8512, with the auxiliary rectangle.
The two parcels are thus unequal in area. However, we know the difference between their areas, as well as the difference between the appurtenant “descendants.” The solution makes use of an unsuspected and elegant ruse and may therefore be difficult to follow.
Lines Obv. 8–10 “raise” the igi of the difference between the two “descendants” to the difference between the two “surfaces.” This means that the text finds the width of a rectangle whose length corresponds to the difference between the partial heights and whose area equals the difference between the partial areas. This width (which is 21) is first memorized and then “joined” to the width of the triangle.
The outcome is a triangle with an attached rectangle—all in all the trapezium shown in Figure 5.1. When prolonging the bar, producing a parallel transversal of the trapezium, we discover that it divides the trapezium into two equal parts—and that is the problem the surveyors
Lines Obv. 11–16 show how they had done it: the square on the bisecting transversal is determined as the average between the squares of the parallel sides. The operations that are used (“making hold” and “breaking”) show that the process is really thought in terms of geometric squares and average. Figure (5.2) shows why the procedure leads to the correct result. By definition, the average is equidistant from the two extremes. Therefore the gnomon between 21 and 39 must equal that between 39 and 51
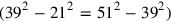 ; half of these gnomons—the two parts of the shaded trapezium—must therefore also be equal. In the first instance this only concerns a trapezium cut out along the diagonal of a square, but we may imagine the square drawn long (into a rectangle) and perhaps twisted into a parallelogram; none of these operations changes the ratio between areas or parallel linear extensions, and they allow the creation of an arbitrary trapezium. This trapezium will still be bisected
; half of these gnomons—the two parts of the shaded trapezium—must therefore also be equal. In the first instance this only concerns a trapezium cut out along the diagonal of a square, but we may imagine the square drawn long (into a rectangle) and perhaps twisted into a parallelogram; none of these operations changes the ratio between areas or parallel linear extensions, and they allow the creation of an arbitrary trapezium. This trapezium will still be bisected
Fig. 5.2: The bisection of the trapezium of BM 8512.
We may take note that the operation of “drawing long” is the
same as that change of scale
Possibly the rule was first found on the basis of concentric squares
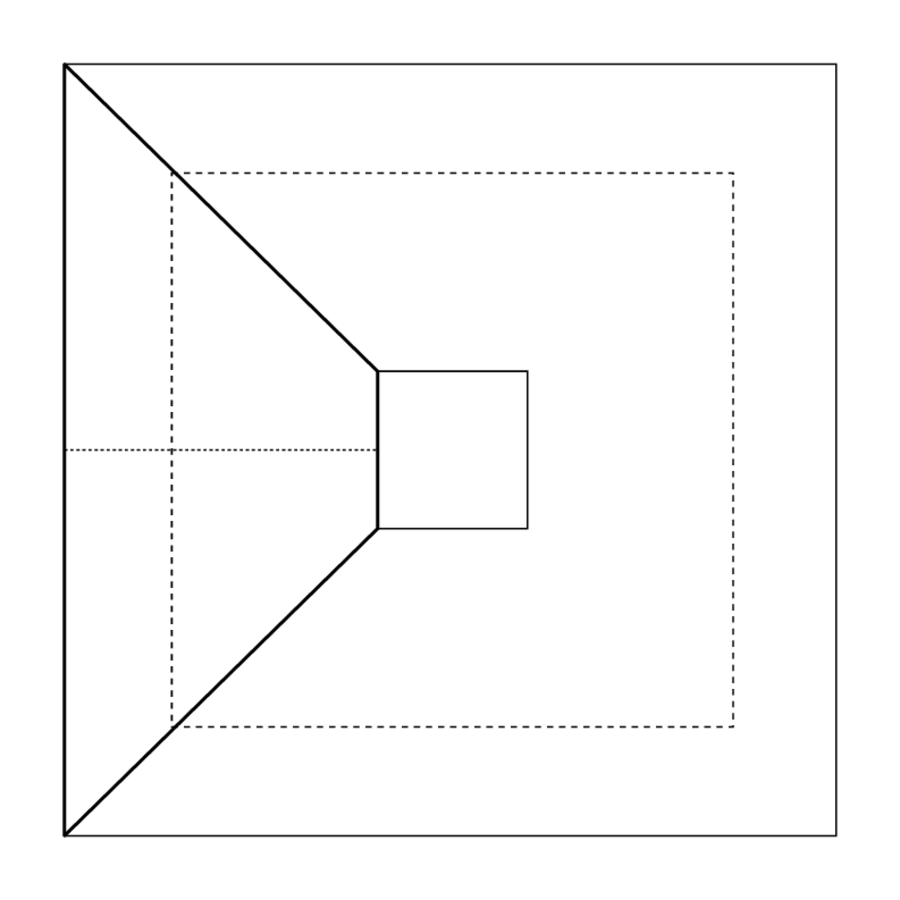
Fig. 5.3: The bisection of the trapezium explained by concentric squares.
Line Obv. 17 thus finds the bisecting transversal; it turns out to be 39, and the “bar” between the two original parcels must therefore be
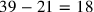 .
.
The next steps may seem strange. Lines Obv. 21–22 appear to calculate the width of the triangle, but this was one of the given magnitudes of the problem. This means no doubt that we have effectively left behind Figure 5.1, and that the argument is now based on something like Figure 5.2. When we eliminate the additional width 21 we are left with a triangle that corresponds to the initial triangle but which is isosceles—see Figure 5.4.
In order to find the “upper descendant” the text makes the false position
Lines Obv. 23–24 calculate that the area of the false triangle is 7‵30. The two areas in white are equal, and their sum must be
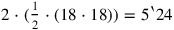 . The shaded area—which corresponds to the difference between the two parcels—must therefore be
. The shaded area—which corresponds to the difference between the two parcels—must therefore be
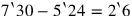 (edge 1–3).
(edge 1–3).
But we know that the difference is 7‵ and not 2‵6. Lines Rev. 1–3 therefore establish that the difference 2‵6 that results from the false position must be multiplied by 3°20′ if we are to find the true difference 7‵. Since the width is already what it should be, it is the length and the “descendants” that must be multiplied by this factor. The “upper descendant” will thus be
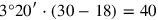 (line Rev. 6). Afterwards everything is quite simple; it could have been even simpler, but the road that is chosen agrees better with the pedagogical
style which we know for example from TMS XVI #1
(line Rev. 6). Afterwards everything is quite simple; it could have been even simpler, but the road that is chosen agrees better with the pedagogical
style which we know for example from TMS XVI #1
The way this problem is solved certainly differs from what we have encountered so far. But there are also common features that become more conspicuous in a bird’s eye view.
The change of scale
Less evident but fundamental is the “analytic”
A solution by equation is always analytical. In order to understand that we may look again at our modern solution of TMS XIII . We do the same with the sales rate (which we call
. We do the same with the sales rate (which we call
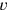 ). The total investment is hence
). The total investment is hence
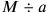 , the total sales price
, the total sales price
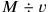 , and the profit therefore
, and the profit therefore
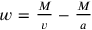 . Then we multiply by
. Then we multiply by
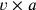 , and so forth.
, and so forth.
That is, we treat
 and
and
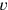 as if they were known numbers; we pretend to have a solution and we describe its characteristics. Afterwards we derive the consequences—and find in the end that
as if they were known numbers; we pretend to have a solution and we describe its characteristics. Afterwards we derive the consequences—and find in the end that
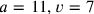 .
.
Even the Old Babylonian cut-and-paste
The solution to the present problem is also analytical. We presuppose that the triangle has been completed by a rectangle in such a way that the prolonged “bar” divides resulting trapezium in equal parts, after which we calculate how much the width of the rectangle must be if that shall be the case; and so on. Even though it has its justification, the distinction between “algebra” (problems that are easily translated into modern equations) and “quasi-algebra”
BM 85200 + VAT 6599 #6
Obv. I
9An excavation. So much as the length, that is the depth. 1 the dirt I have torn out. My ground and the dirt I have heaped, 1°10′. Length and width, 50′. Length, width, what?
10You, 50′ to 1, the conversion, raise, 50′ you see. 50′ to 12 raise, 10 you see.
11Make 50′ confront itself,
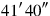 you see; to 10 raise,
you see; to 10 raise,
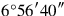 you see. Its igi detach,
you see. Its igi detach,
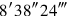 you see;
you see;
12to 1°10′ raise,
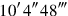 you see, 36′, 24′, 42′ are equals.
you see, 36′, 24′, 42′ are equals.
1336′ to 50′ raise, 30′, the length. 24′ to 50′ raise, 20′, the width; 36′ to 10 raise, 6, the depth.
14The procedure.
This is a problem of the third degree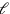 [nindan], width
[nindan], width
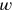 [nindan] and depth
[nindan] and depth
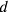 [kùš]. The length is equal to the depth, but because of the use of different metrologies in the two directions that means that
[kùš]. The length is equal to the depth, but because of the use of different metrologies in the two directions that means that
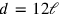 .
.
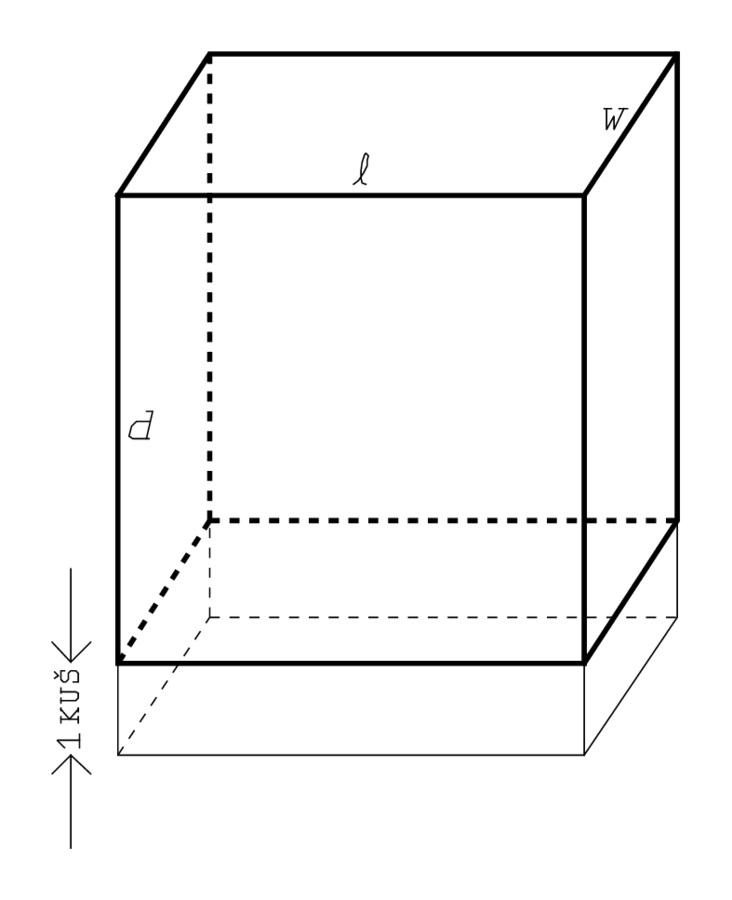
Fig. 5.5: The excavation extended 1 kùš downwards.
Further the sum of the length and the width is
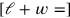 50′, and the sum of the volume of dirt that has been “torn out,” that is, dug out 2 and the “ground” (the base) is
50′, and the sum of the volume of dirt that has been “torn out,” that is, dug out 2 and the “ground” (the base) is
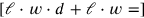 1°10′. This latter equation can be transformed into
1°10′. This latter equation can be transformed into
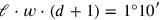 —that is, if the excavation had been dug 1 kùš deeper, its volume would have equalled 1°10′ [nindan2
—that is, if the excavation had been dug 1 kùš deeper, its volume would have equalled 1°10′ [nindan2
 kùš] (see Figure 5.5).3
kùš] (see Figure 5.5).3
The solution is based on a subtle variant of the false position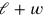 . In horizontal
measure, its side is
. In horizontal
measure, its side is
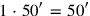 [nindan], since “the conversion” of nindan into nindan asks for a multiplication by 1. In vertical measure, it is
[nindan], since “the conversion” of nindan into nindan asks for a multiplication by 1. In vertical measure, it is
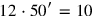 kùš, since “the conversion” of nindan into kùš implies a multiplication by 12 (both conversions take place in line 10).
kùš, since “the conversion” of nindan into kùš implies a multiplication by 12 (both conversions take place in line 10).
Lines 11–12 find the volume of the reference cube to be
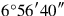 . This volume is contained
. This volume is contained
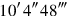 times in the extended excavation.
times in the extended excavation.
We should now imagine that the sides of the extended excavation are measured by the corresponding sides of the reference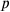 is the number of times the length
is the number of times the length
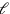 is measured by 50′ nindan,
is measured by 50′ nindan,
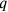 the number of times the width
the number of times the width
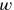 is measured by 50′ nindan, and
is measured by 50′ nindan, and
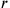 the number of times the depth
the number of times the depth
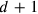 kùš is measured by 10 kùš (= 50´ nindan), then
kùš is measured by 10 kùš (= 50´ nindan), then
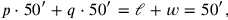
|
and therefore
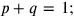
|
further
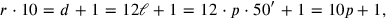
|
whence
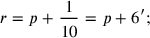
|
and finally
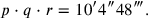
|
We therefore have to express
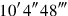 as the product of three factors
as the product of three factors
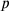 ,
,
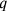 and
and
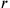 that fulfil these conditions. That is what the text does in line 12, where the factors appear as the “equals” 36′, 24′ and 42′. Afterwards, line 13 finds
that fulfil these conditions. That is what the text does in line 12, where the factors appear as the “equals” 36′, 24′ and 42′. Afterwards, line 13 finds
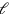 ,
,
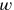 and
and
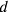 .
.
The factorization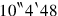 (
(
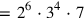 ) as the product of three numbers
) as the product of three numbers
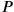 ,
,
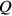 and
and
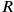 where
where
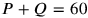 ,
,
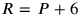 .4 Knowing the general character of Old Babylonian mathematics we may even claim that the text can only allow itself to draw the answer from the sleeves because it would be possible (albeit somewhat laborious) to find it without magic. Let us first assume that
.4 Knowing the general character of Old Babylonian mathematics we may even claim that the text can only allow itself to draw the answer from the sleeves because it would be possible (albeit somewhat laborious) to find it without magic. Let us first assume that
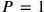 ; then, since
; then, since
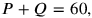
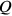 will be
will be
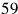 , which is impossible; the hypotheses
, which is impossible; the hypotheses
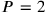 and
and
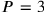 can be rejected for analogous reasons;
can be rejected for analogous reasons;
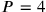 gives
gives
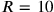 , which is also excluded—
, which is also excluded—
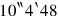 contains no factor
contains no factor
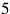 ;
;
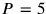 is impossible in itself;
is impossible in itself;
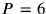 gives
gives
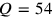 and
and
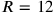 , which must be rejected, both because the factor
, which must be rejected, both because the factor
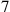 is missing and because control shows the product not to be what is required. The next value
is missing and because control shows the product not to be what is required. The next value
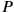 which does not lead to impossible values for
which does not lead to impossible values for
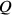 or
or
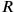 is
is
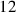 , but it must be rejected for the same reasons;
, but it must be rejected for the same reasons;
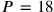 is impossible because the product is only around half of what is needed.
is impossible because the product is only around half of what is needed.
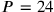 and
and
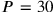 must be rejected for the same reasons as
must be rejected for the same reasons as
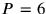 . Finally we arrive at
. Finally we arrive at
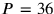 , a value that fits. If we had counted prime factors it would have been even easier,
, a value that fits. If we had counted prime factors it would have been even easier,
It must be emphasized, however, that this method only works because a simple solution exists. Thereby the problem differs fundamentally from those of the second degree, where a good approximation to that which “is equal” would give an almost correct solution (and the Babylonians knew well to find approximate square
Our text speaks of three “equals”
Other problems from the same tablet speak of a single “equal”; that is the case when the volume of the excavation measured by the reference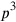 or as
or as
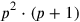 . Tables
. Tables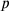 appears precisely as “the equal;”
appears precisely as “the equal;”
As in the second-degree algebra, the treatment of the third-degree
Apart from that, only rather peripheral characteristics connect the second and the third degree: the terminology for operations, the use of tables, the fundamental arithmetical operations.
Other problems on the same tablet (all dealing with parallelepipedal “excavations”) are reduced to problems of the second or even the first degree. These are solved by the techniques we already know, and never by factorization
BM 15285 #24
1
11 uš the confrontation.
2Inside, 16 confrontations
3I have laid down. Their surface what?
The small problem that precedes is extracted from a tablet containing some 40 problems
The above text does not explain the procedure—none of the problems on the tablet
In line 3 it is seen that the verb translated “to lay down”
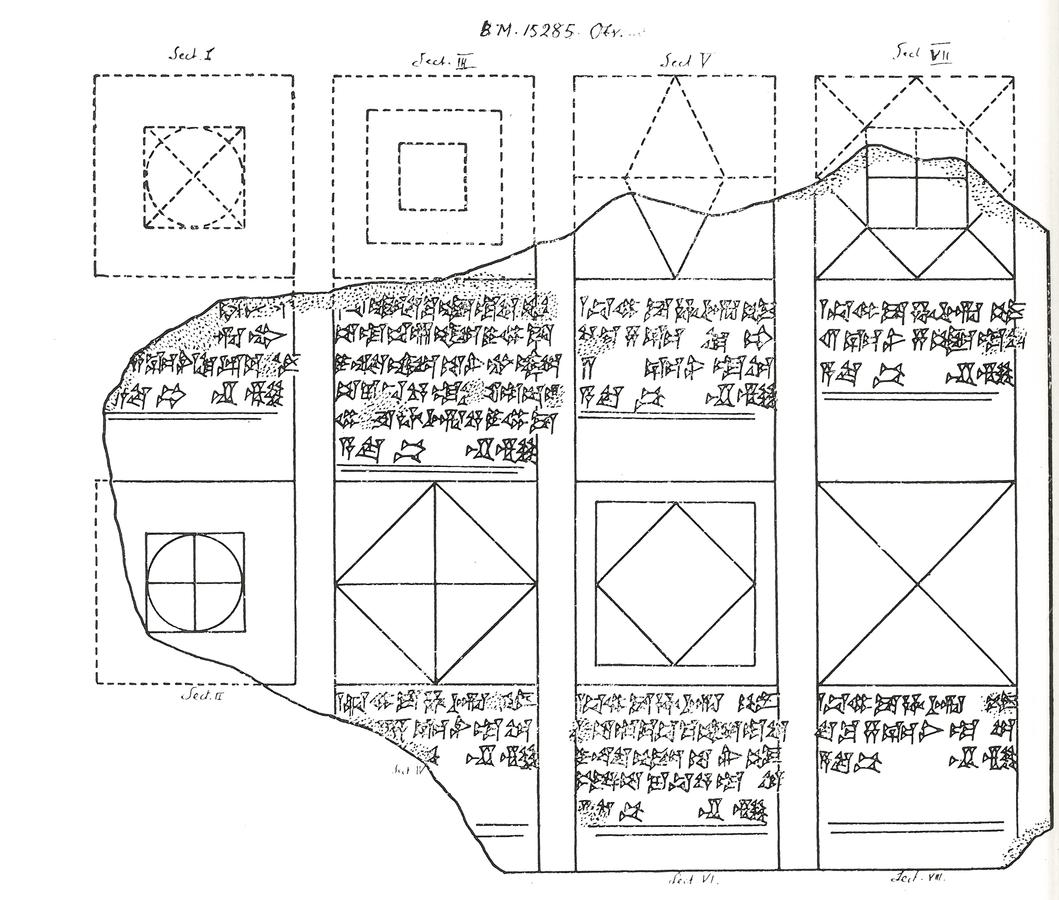
Fig. 5.6: The obverse of the principal fragment of the tablet BM 15285. After C. J. Gadd, “Forms and Colours”. Revue d’Assyriologie 19 (1922), 149–159, here p. 156.
Footnotes
The antithesis of the “analytical” method is the “synthesis, in which the solution is constructed directly, after which this solution is shown to be indeed valid.” This is the proof style of Euclid’s Elements, and since antiquity there has been the consistent complaint that this makes it more difficult than necessary to understand the work: the student sees well that each step of a proof is correct, and therefore has to accept the end result as irrefutable—but one does not understand the reasons that make the author take the single step. In this way, the author appears shrewd rather than really pedagogical. Since antiquity Euclid (or his predecessors) have also been suspected to have first found their constructions and proofs by means of analysis, constructing the solution in the second instance but hiding their traces.
The text uses the same verb “to tear out” as for the subtractive operation.
The statement also refers to “1 the dirt that I have torn out,” but this information is not used. It is another example of a magnitude that is known but not given; knowing its numerical value allows the teacher to make a distinction between the real excavation (“1 the dirt”) and the volume of the excavation extended downwards by 1 kùš (“1°10′, the dirt”).
In order to have integers we here introduce P=60p=1‵p, Q = 1‵q, R = 1‵r. Then PQR = 1‷pqr =
 .
.

