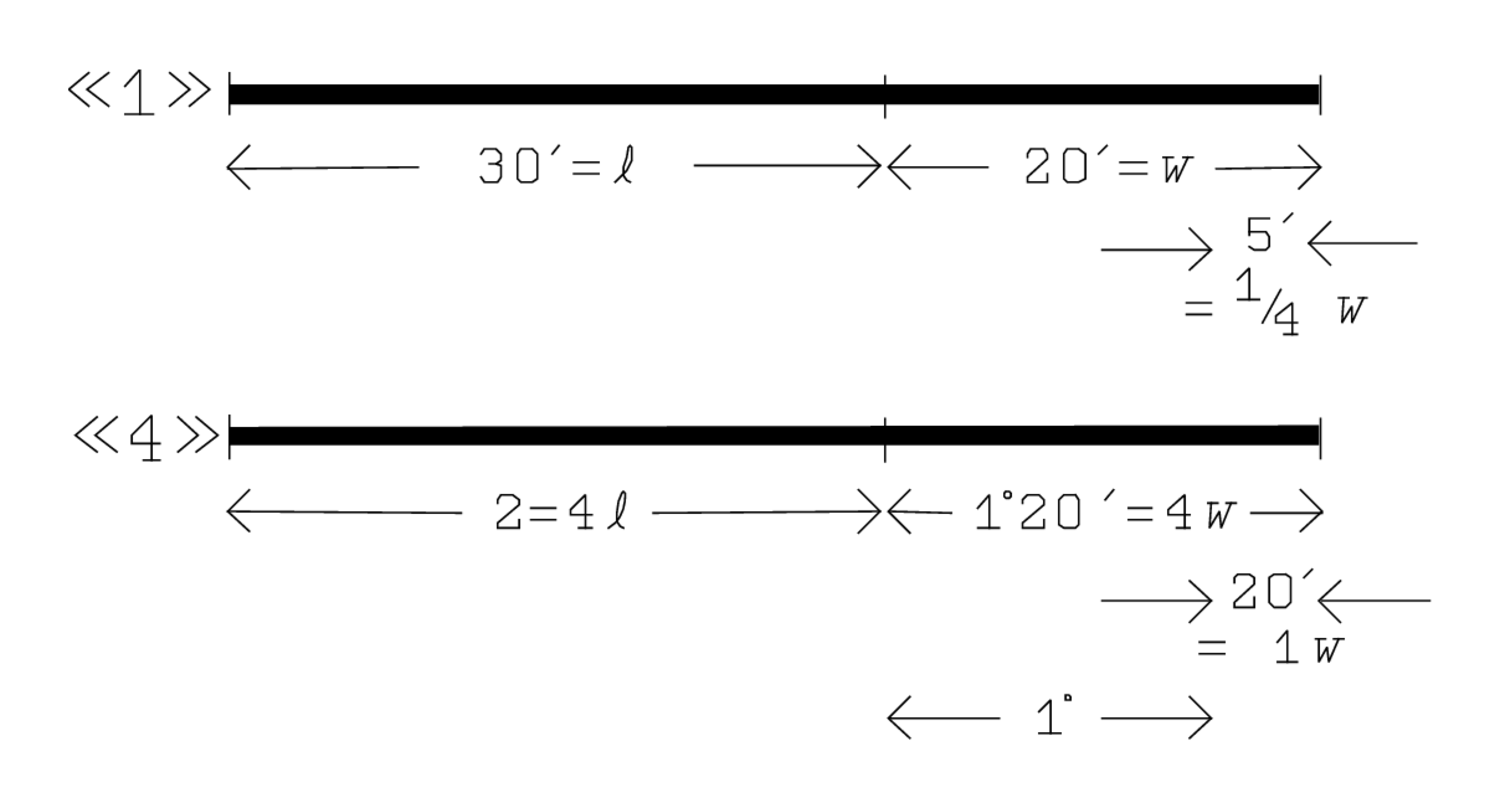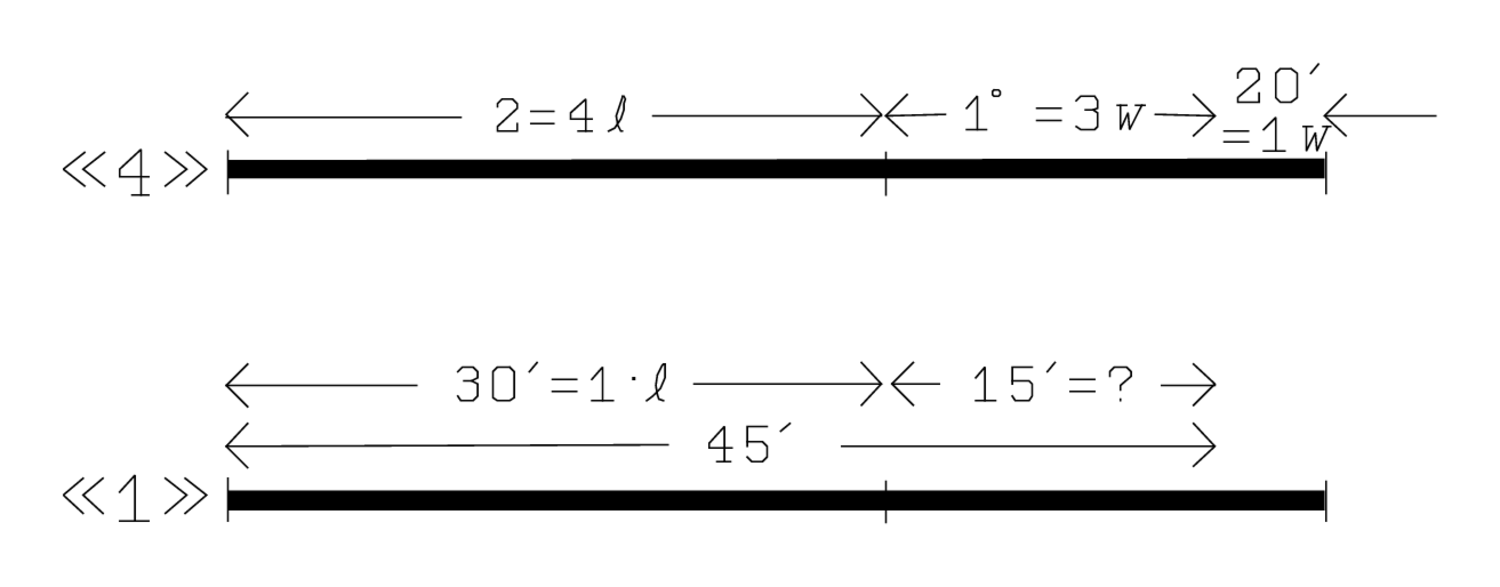Our main topic will be the Old Babylonian treatment of second-degree
equations.1 However, the solution of second-degree equations or equation systems often asks for first-degree
TMS XVI #1
1The 4th of the width, from the length and the width I have torn out, 45′. You, 45′
2to 4 raise, 3 you see. 3, what is that? 4 and 1 posit,
350′ and 5′, to tear out, posit. 5′ to 4 raise, 1 width. 20′ to 4 raise,
41°20′ you
 see
see
 ,2 4 widths. 30′ to 4 raise, 2 you
,2 4 widths. 30′ to 4 raise, 2 you
 see
see
 , 4 lengths. 20′, 1 width, to tear out,
, 4 lengths. 20′, 1 width, to tear out,
5from 1°20′, 4 widths, tear out, 1 you see. 2, the lengths, and 1, 3 widths, heap, 3 you see.
6igi 4 detach, 15′ you see. 15′ to 2, lengths, raise, 30′ you
 see
see
 , 30′ the length.
, 30′ the length.
715′ to 1 raise, 15′ the contribution of the width. 30′ and 15′ hold.
8Since “The 4th of the width, to tear out,” it is said to you, from 4, 1 tear out, 3 you see.
9igi 4 de
 tach
tach
 , 15′ you see, 15′ to 3 raise, 45′ you
, 15′ you see, 15′ to 3 raise, 45′ you
 see
see
 , 45′ as much as (there is) of widths.
, 45′ as much as (there is) of widths.
101 as much as (there is) of lengths posit. 20, the true width take, 20 to 1′ raise, 20′ you see.
1120′ to 45′ raise, 15′ you see. 15′ from 3015′ tear out,
1230′ you see, 30′ the length.
This text differs in character from the immense majority of Old
Babylonian mathematical texts: it does not state a problem, and it
solves none. Instead, it gives a didactic explanation
Even though many of the terms that appear in the translation were already explained in the section “A new interpretation,” it may be useful to go through the text word for word.
Line 1 formulates an equation: The 4th of the width, from the length and the width I have torn out, 45′.
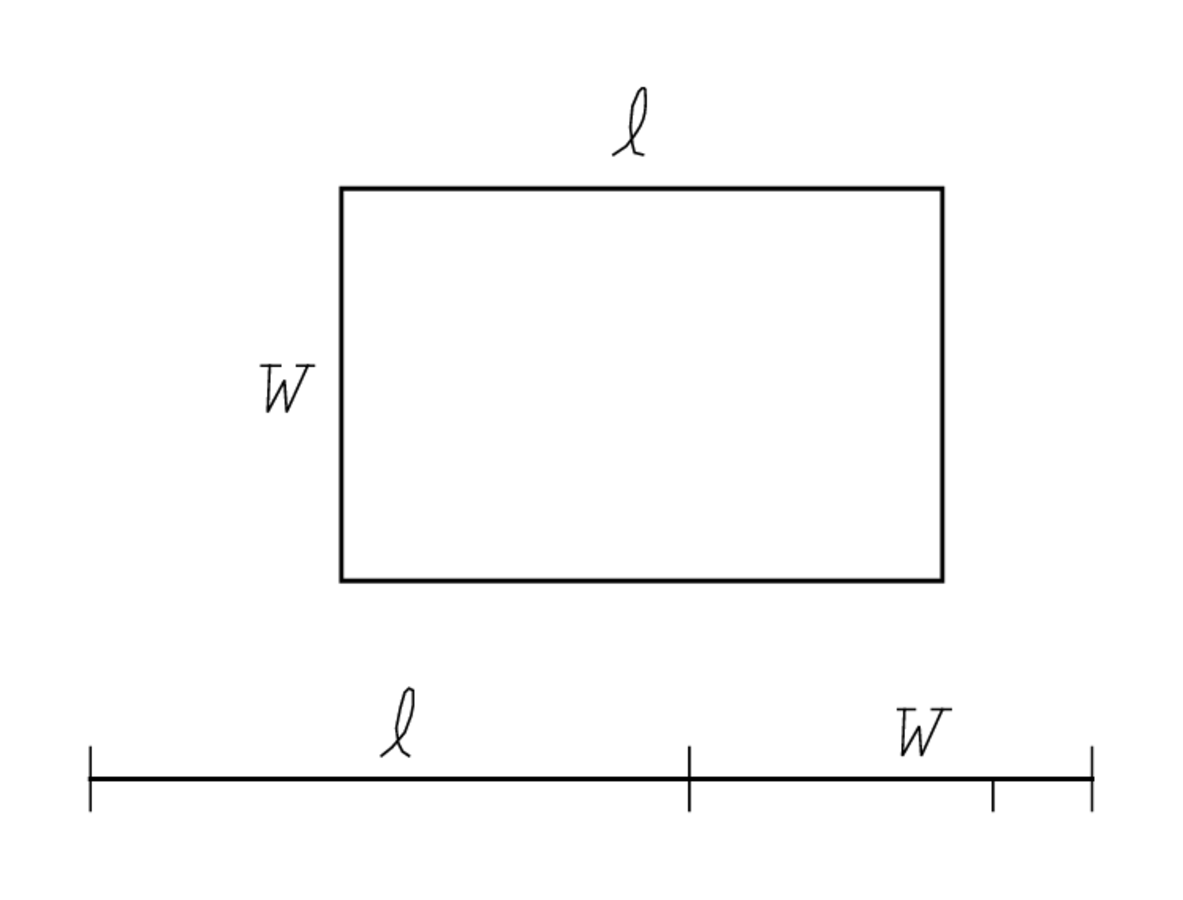
The equation thus concerns a length and a width. That tells us that
the object is a rectangle—from the Old Babylonian point of view, the
rectangle is the simplest figure determined by a length and a width
alone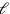 is the length and
is the length and
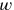 the width, we may express the equation in symbols in this way:
the width, we may express the equation in symbols in this way:
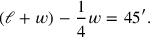
|
Something, however, is lost in this translation. Indeed, the length and the width is a condensed expression for a “heaping,”
Once the length and the width have been “heaped,” it is possible to “tear out”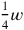 , since this entity is a part of the width and hence also of the total. To “tear out,” as we remember, is the inverse operation of “joining,” and thus the removal of a magnitude from another one of which it is a part (see Figure 2.2).
, since this entity is a part of the width and hence also of the total. To “tear out,” as we remember, is the inverse operation of “joining,” and thus the removal of a magnitude from another one of which it is a part (see Figure 2.2).
Line 1 shows the nature of a Babylonian
Next, lines 1 and 2 ask the student to multiply the 45′ (on the
right-hand side of the version in symbols) by 4: You, 45′ to 4 raise, 3 you see. To “raise,”
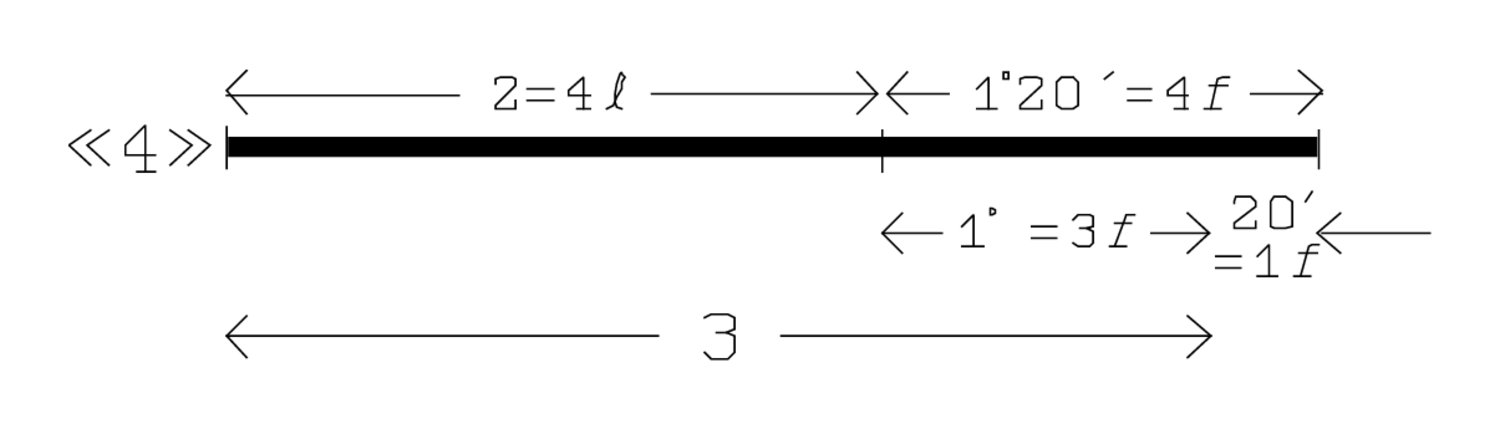
The answer to this question is found in lines 2–5. 4 and 1 posit: First, the student should “posit”
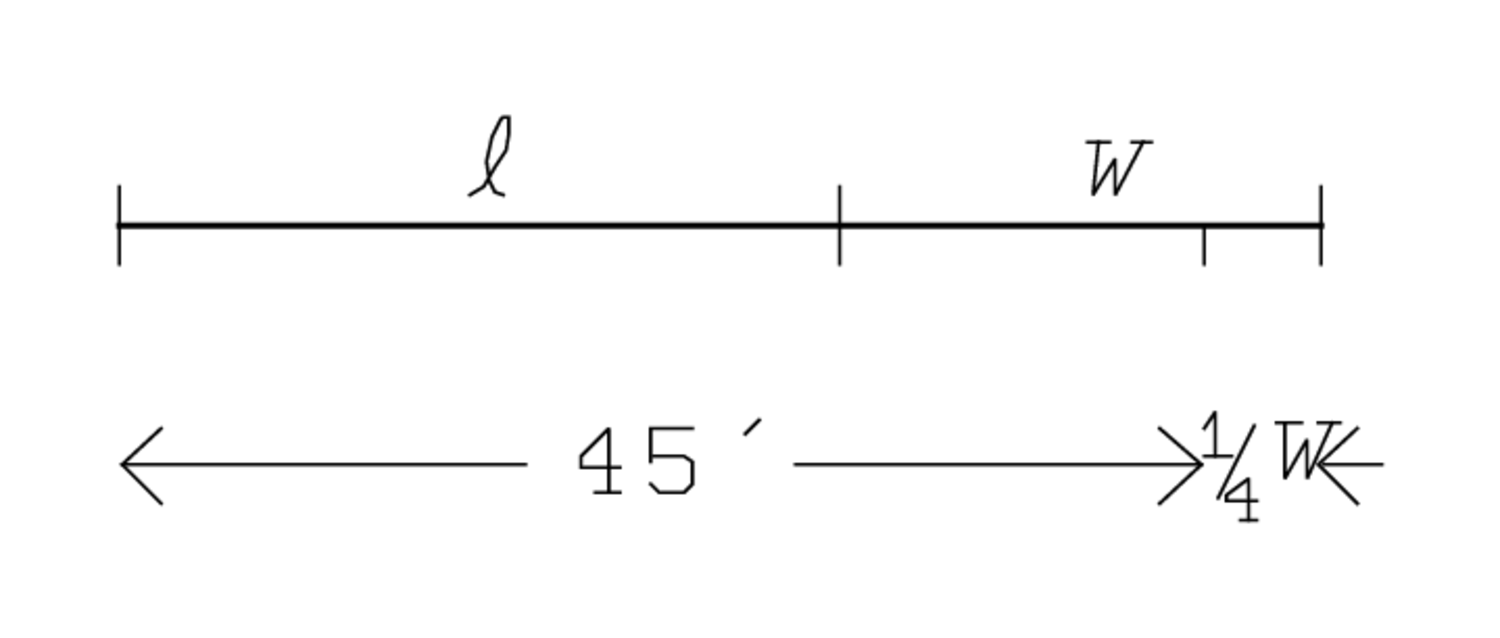
50′ and 5′, to tear out, posit: the numbers 50′ and 5′ are placed
on level «1» of the diagram. This should surprise us: it shows that the
student is supposed to know already that the width is 20′ and the
length is 30′. If he did not, he would not understand that
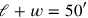 and that
and that
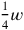 (that which is to be torn out) is 5′. For the sake of clarity not only the numbers 50′ and 5′ but also 30′ and 20′ are
indicated at level «1» in our diagram even though the text does not
speak about them.
(that which is to be torn out) is 5′. For the sake of clarity not only the numbers 50′ and 5′ but also 30′ and 20′ are
indicated at level «1» in our diagram even though the text does not
speak about them.
Lines 3–5 prove even more convincingly that the student is supposed to know already the solution to the problem (which is thus only a quasi-problem). The aim of the text is thus not to find a solution. As already stated, it is to explain the concepts and procedures that serve to understand and reduce the equation.
These lines explain how and why the initial equation
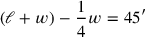
|
is transformed into

|
through multiplication by 4.
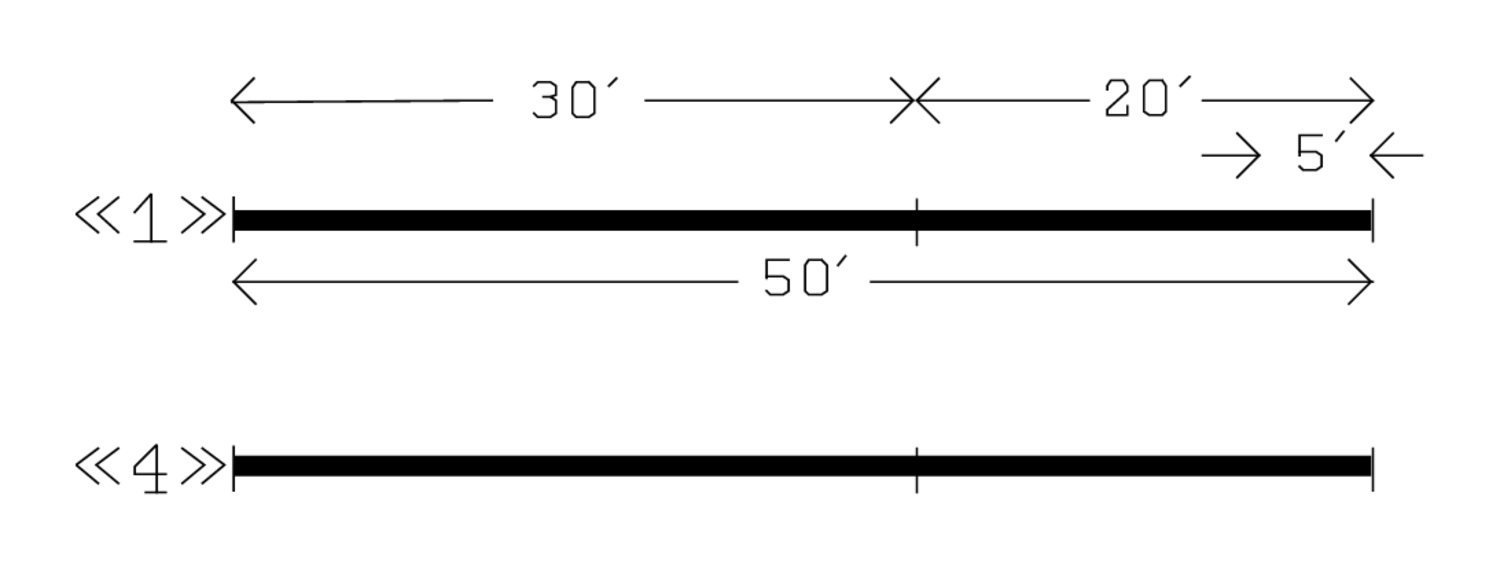
This calculation can be followed in Figure 2.4, where the numbers on level «1» are multiplied by 4, giving thereby rise to those of level «4»:
5′ to 4 raise, 1 width: 5′, that is, the
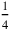 of the width, is multiplied by 4, from which results 20′, that is, one width.
of the width, is multiplied by 4, from which results 20′, that is, one width.
20′ to 4 raise, 1°20′ you
 see
see
 , 4 widths: 20′, that is, 1 width, is multiplied by 4, from which comes 1°20′, thus 4 widths.
, 4 widths: 20′, that is, 1 width, is multiplied by 4, from which comes 1°20′, thus 4 widths.
30′ to 4 raise, 2 you
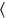 see
see
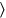 , 4 lengths: 30′, that is 1 length, is multiplied by 4. This gives 2, 4 lengths.
, 4 lengths: 30′, that is 1 length, is multiplied by 4. This gives 2, 4 lengths.
After having multiplied all the numbers of level «1» by 4, and finding thus their counterparts on level «4», the text indicates (lines 4 and 5) what remains when 1 width is eliminated from 4 widths: 20′, 1 width, to tear out, from 1°20′, 4 widths, tear out, 1 you see.
Finally, the individual constituents of the sum
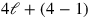
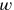 are identified, as shown in Figure 2.5 2, the lengths, and 1, 3 widths, heap, 3 you see: 2, that is, 4 lengths, and 1, that is,
are identified, as shown in Figure 2.5 2, the lengths, and 1, 3 widths, heap, 3 you see: 2, that is, 4 lengths, and 1, that is,
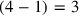 widths, are added. This gives the number 3. We have now found the answer to the question of line 2, 3 you see. 3, what is that?
widths, are added. This gives the number 3. We have now found the answer to the question of line 2, 3 you see. 3, what is that?
But the lesson does not stop here. While lines 1–5 explain how the equation
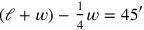 can be transformed into
can be transformed into
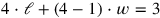 , what follows in lines 6–10 leads, through division by 4, to a transformation of this equation into
, what follows in lines 6–10 leads, through division by 4, to a transformation of this equation into
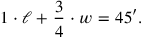
|
For the Babylonians, division by 4 is indeed effectuated as a multiplication
by
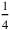 . Therefore, line 6 states that
. Therefore, line 6 states that
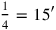 : igi 4 detach, 15′ you see. igi 4 can be found in the table
: igi 4 detach, 15′ you see. igi 4 can be found in the table
Figure 2.6 shows that this corresponds to a return to level «1»:
15′ to 2, lengths, raise, 30′ you
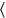 see
see
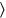 , 30′ the length: 2, that is, 4 lengths, when multiplied by
, 30′ the length: 2, that is, 4 lengths, when multiplied by
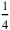 gives 30′, that is, 1 length.
gives 30′, that is, 1 length.
15′ to 1 raise, 15′ the contribution of the width. (line 7): 1, that is, 3 widths, is multiplied by
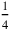 , which gives 15′, the contribution of the width to the sum 45′. The quantity of widths to which this contribution
corresponds is determined in line 8 and 9. In the meantime, the
contributions of the length and the width are memorized: 30′ and 15′ hold—a shorter expression for may you head hold, the formulation used in other texts. We notice the contrast to the material taking note of the numbers 1, 4, 50′ and 5′ by “positing” in the beginning.
, which gives 15′, the contribution of the width to the sum 45′. The quantity of widths to which this contribution
corresponds is determined in line 8 and 9. In the meantime, the
contributions of the length and the width are memorized: 30′ and 15′ hold—a shorter expression for may you head hold, the formulation used in other texts. We notice the contrast to the material taking note of the numbers 1, 4, 50′ and 5′ by “positing” in the beginning.
The contribution of the width is thus 15′. The end of line 9 indicates that the number of widths to which that corresponds—the coefficient of the width, in our language—is
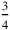 (= 45′): 45′ as much as (there is) of widths. The argument leading to this is of a type
known as “simple false position .”4
(= 45′): 45′ as much as (there is) of widths. The argument leading to this is of a type
known as “simple false position .”4
Line 8 quotes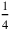 has been removed.
has been removed.
For the sake of convenience, it is “posited” that the quantity of widths is 4 (this is the “false position”).
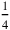 of 4 equals 1 (the text gives this number without calculation). When it is eliminated, 3 remains: from 4, 1 tear out, 3 you see.
of 4 equals 1 (the text gives this number without calculation). When it is eliminated, 3 remains: from 4, 1 tear out, 3 you see.
In order to see to which part of the falsely posited 4 this 3 corresponds, we multiply by
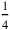 . Even though this was already said in line 6, it is repeated in line 9 that
. Even though this was already said in line 6, it is repeated in line 9 that
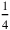 corresponds to 15′: igi 4 de
corresponds to 15′: igi 4 de
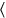 tach
tach
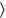 , 15′ you see.
, 15′ you see.
Still in line 9, multiplication by 3 gives the coefficient of the width as 45′ (=
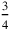 ): 15′ to 3 raise, 45′ you
): 15′ to 3 raise, 45′ you
 see
see
 , 45′ as much as (there is) of widths.
, 45′ as much as (there is) of widths.
Without calculating it line 10 announces that the coefficient of the
length is 1. We know indeed from line 1 that a sole length enters into
the 45′, without addition nor subtraction. We have thus explained how
the equation
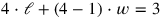 is transformed into
is transformed into
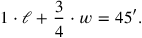
|
The end of line 10 presents us with a small riddle: what is the
relation between the “true width” and the width which figures in the
equations?
The explanation could be the following: a true field might measure
30 [nindan] by 20 [nindan] (c. 180 m by 120 m, that is,
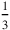 bùr
bùr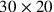 in the courtyard of the schoolmaster’s house (or any other school
in the courtyard of the schoolmaster’s house (or any other school
In any case, in line 11 it is found again that the width contributes with 15′, namely by multiplying 20′ (1 width) by the coefficient 45′: 20′ to 45′ raise, 15′ you see.
In the end, the contribution of the width is eliminated from 45′ (already written 3015, that is, as the sum of 30′ and 15′, in agreement with the partition memorized in the end of line 7). 30′ remains, that is, the length: 15′ from 3015′ tear out, 30′ you see, 30′ the length.
All in all, a nice pedagogical explanation
Before leaving the text, we may linger on the actors that appear, and which recur in most of those texts that state a problem together with the procedure leading to its solution.5 Firstly, a “voice” speaking in the first person singular describes the situation which he has established, and formulates the question. Next a different voice addresses the student, giving orders in the imperative or in the second person singular, present tense; this voice cannot be identical with the one that stated the problem, since it often quotes it in the third person, “since he has said.”
In a school context, one may imagine that the voice that states the problem is that of the school master, and that the one which addresses the student is an assistant or instructor—“edubba texts,”6 literary texts about the school and about school
TMS VII #2
17The fourth of the width to the length I have joined, its seventh
18until 11 I have gone, over the heap
19of length and width 5′ it went beyond. You, 4 posit;
207 posit; 11 posit; and 5′ posit.
215′ to 7 raise, 35′ you see.
2230′ and 5′ posit. 5′ to 11 raise, 55′ you see.
2330′, 20′, and 5′, to tear out, posit. 5′ to 4
24raise, 20′ you see, 20 the width. 30′ to 4 raise:
252 you see, 2, lengths. 20′ from 20′ tear out.
2630′ from 2 tear out, 1°30′ posit, and 5′ to ¿50′, the heap of length and width, join?
277 to 4, of the fourth, raise, 28 you see.
2811, the heaps, from 28 tear out, 17 you see.
29From 4, of the fourth, 1 tear out, 3 you see.
30igi 3 detach, 20′ you see. 20′ to 17 raise,
315°40′ you see, 5°40′, (for) the length. 20′ to 5′, the going-beyond, raise,
32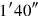 you see,
you see,
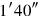 , the to-be-joined of the length. 5°40′, (for) the length,
, the to-be-joined of the length. 5°40′, (for) the length,
33from 11, heaps, tear out, 5°20′ you see.
34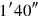 to 5′, the going-beyond, join,
to 5′, the going-beyond, join,
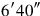 you see.
you see.
35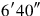 , the to-be-torn-out of the width. 5′, the step,
, the to-be-torn-out of the width. 5′, the step,
36to 5°40′, lengths, raise,
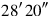 you see.
you see.
37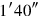 , the to-be-joined of the length, to
, the to-be-joined of the length, to
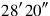 join,
join,
3830′ you see, 30′ the length. 5′ to 5°20′
39raise:
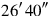 you see.
you see.
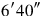 ,
,
40the to-be-torn-out of the width, from
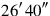 tear out,
tear out,
4120′ you see, 20′ the width.
This is the second, difficult problem from a tablet. The first, easy one (found on page
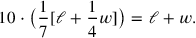
|
After reduction, this gives the equation
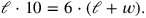
|
This is an “indeterminate”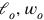 ), all the others can be written (
), all the others can be written (
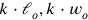 ). The text finds one by taking the first factor to the left to be equal to the first factor to the right (thus
). The text finds one by taking the first factor to the left to be equal to the first factor to the right (thus
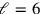 ), and the second factor to the right to be equal to the second factor to the right (thus
), and the second factor to the right to be equal to the second factor to the right (thus
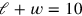 , whence
, whence
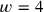 ). Afterwards the solution that has been tacitly aimed at from the beginning is obtained through “raising” to 5′ (the “step”
). Afterwards the solution that has been tacitly aimed at from the beginning is obtained through “raising” to 5′ (the “step”
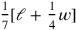 that has been “gone” 10 times). Indeed, if
that has been “gone” 10 times). Indeed, if
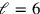 ,
,
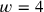 , then the “step” is 1; if we want it to be 5′ (which corresponds to the normal dimensions of a “school rectangle,”
, then the “step” is 1; if we want it to be 5′ (which corresponds to the normal dimensions of a “school rectangle,”
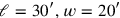 ), then the solution must be multiplied by this value. All of this—which is not obvious—is useful for understanding the second problem.
), then the solution must be multiplied by this value. All of this—which is not obvious—is useful for understanding the second problem.
The first problem is “homogeneous”—all its terms are in the first degree in
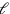 and
and
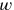 . The second, the one translated above, is inhomogeneous, and can be expressed in symbols in this way:
. The second, the one translated above, is inhomogeneous, and can be expressed in symbols in this way:
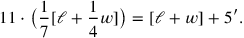
|
We take note that
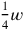 is “joined” to the length; that we take
is “joined” to the length; that we take
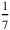 of the outcome; and that afterwards we “go” this segment 11 times. What results “goes beyond” the “heap” of length and width by 5′. The “heap” is thus no part of what results from the repetition of the step—if it were it could have been “torn out.”
of the outcome; and that afterwards we “go” this segment 11 times. What results “goes beyond” the “heap” of length and width by 5′. The “heap” is thus no part of what results from the repetition of the step—if it were it could have been “torn out.”
The solution begins with a pedagogical explanation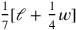 —the raising is a verification that it is really the 7th—and not the “going-beyond” referred to in line 20. Once again the student is supposed to understand that the text is based on the rectangle
—the raising is a verification that it is really the 7th—and not the “going-beyond” referred to in line 20. Once again the student is supposed to understand that the text is based on the rectangle
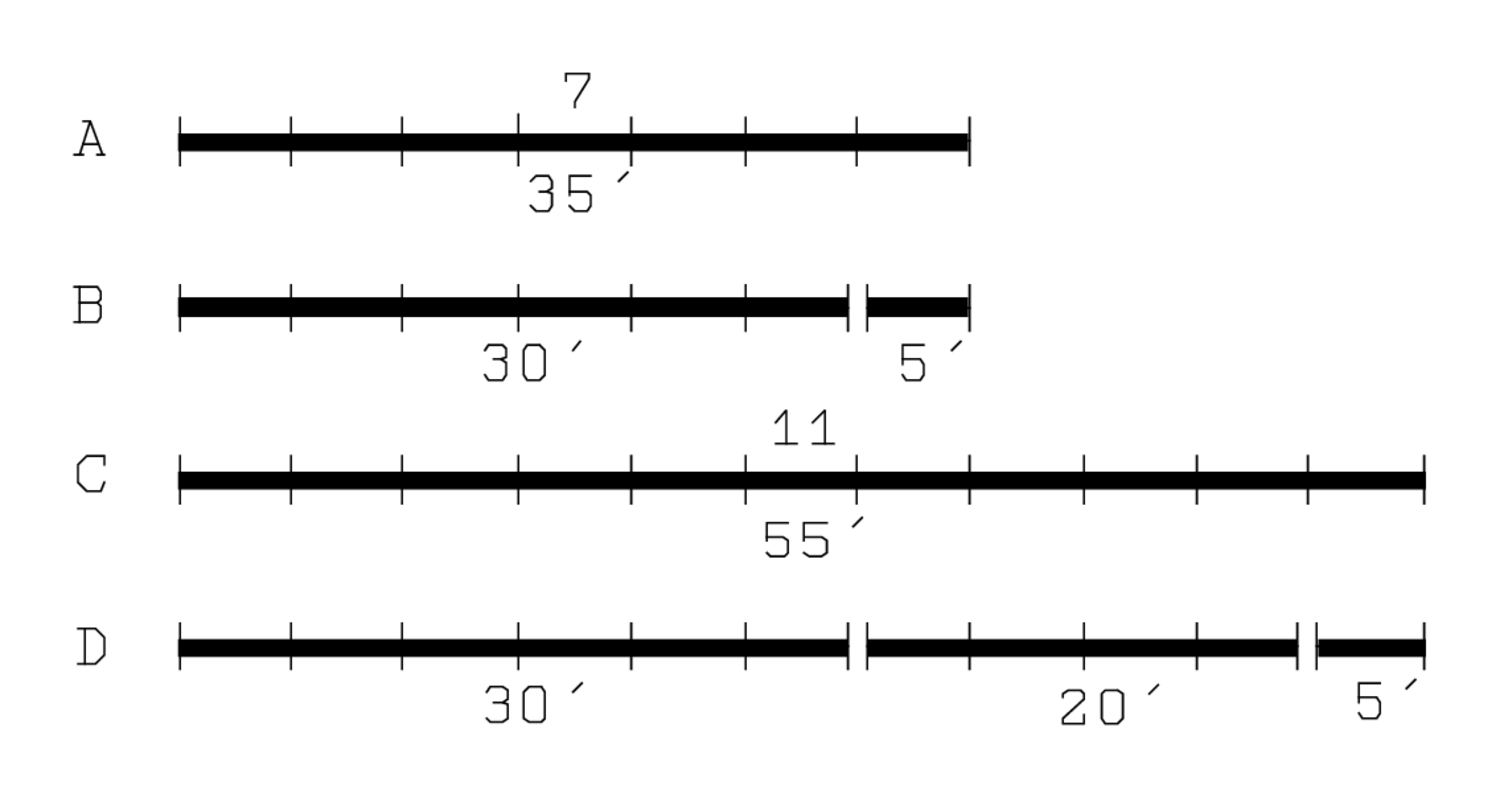
 (30′, 20′). Having this configuration in mind we will be able to follow the explanation of lines 21 to 23 on Figure 2.7: when the “step” 5′ is “raised” to 7, we get 35′ (A), which can be decomposed as
(30′, 20′). Having this configuration in mind we will be able to follow the explanation of lines 21 to 23 on Figure 2.7: when the “step” 5′ is “raised” to 7, we get 35′ (A), which can be decomposed as
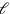 and
and
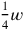 (B). When it is “raised” to 11 we find 55′ (C), which can be decomposed as
(B). When it is “raised” to 11 we find 55′ (C), which can be decomposed as
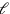 ,
,
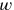 , and 5′ (D).
, and 5′ (D).
Next follows the prescription for solving the equation; is it still formulated in such a way that the solution is supposed to be known. “Raising” to 4 (lines 23 to 25) gives the equivalent of the symbolic equation
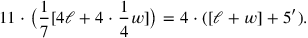
|
Not having access to our symbols, the text speaks of
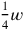 as 5′, finds that
as 5′, finds that
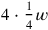 is equal to 20′, and identifies that with the width (line 24); then
is equal to 20′, and identifies that with the width (line 24); then
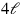 appears as 2, said to represent lengths (line 25).
appears as 2, said to represent lengths (line 25).
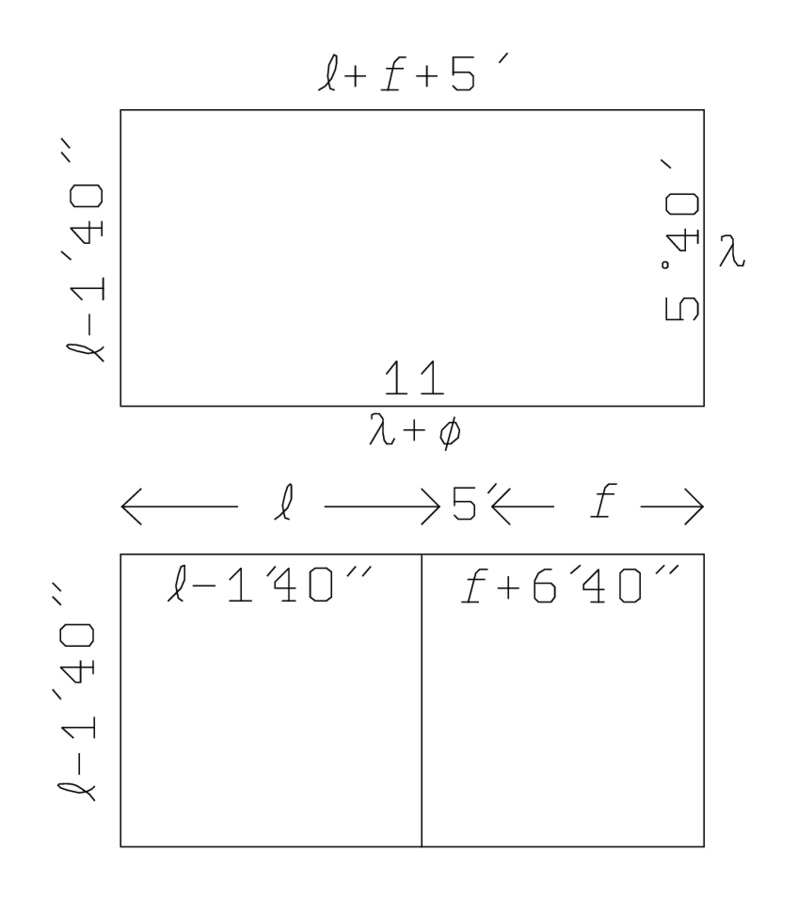
Now, by means of a ruse which is elegant but not easy to follow, the equation is made homogeneous. The text decomposes
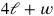 as
as
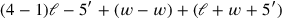
|
and “raises” the whole equation to 7. We may follow the calculation in modern symbolic translation:
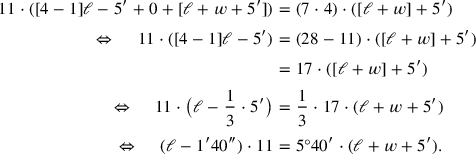
|
However, the Babylonians did not operate with such equations; they are likely to have inscribed the numbers along the lines of a diagram (see Figure 2.8); that is the reason that the “coefficient”
 does not need to appear before line 29.
does not need to appear before line 29.
As in the first problem of the text, a solution to the homogeneous equation is found by identification of the factors “to the left” with those “to the right” (which is the reason that the factors have been inverted on the left-hand side of the last equation):
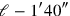 (now called “the length” and therefore designated
(now called “the length” and therefore designated
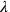 in Figure 2.8 thus corresponds to 5°40′, while
in Figure 2.8 thus corresponds to 5°40′, while
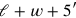 (referred to as “the heap” of the new length
(referred to as “the heap” of the new length
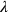 and a new width
and a new width
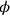 , that is,
, that is,
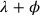 ) equals 11;
) equals 11;
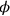 must therefore be
must therefore be
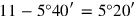 . Next the text determines the “to-be-joined” (wāṣbum) of the length, that is, that which must be joined to the length
. Next the text determines the “to-be-joined” (wāṣbum) of the length, that is, that which must be joined to the length
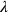 in order to produce the original length
in order to produce the original length
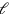 : it equals
: it equals
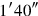 , since
, since
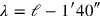 . Further it finds “the to-be-torn-out” (nāsum) of the width, that is, that which must be “torn out” from
. Further it finds “the to-be-torn-out” (nāsum) of the width, that is, that which must be “torn out” from
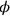 in order to produce
in order to produce
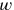 . Since
. Since
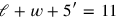 ,
,
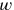 must equal
must equal
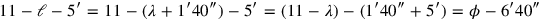 ; the “to-be-torn-out” is thus
; the “to-be-torn-out” is thus
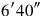 .
.
But “joining” to
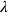 and “tearing out” from
and “tearing out” from
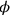 only gives a possible solution, not the one which is intended. In order to have the values for
only gives a possible solution, not the one which is intended. In order to have the values for
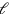 and
and
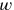 that are aimed at, the step 5′ is “raised” (as in the first problem) to 5°40′ and 5°20. This gives, respectively,
that are aimed at, the step 5′ is “raised” (as in the first problem) to 5°40′ and 5°20. This gives, respectively,
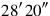 and
and
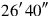 ; by “joining” to the former its “to-be-joined” and by “tearing out” from the latter its “to-be-torn-out” we finally get
; by “joining” to the former its “to-be-joined” and by “tearing out” from the latter its “to-be-torn-out” we finally get
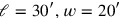 .
.
We must take note of the mastery with which the author avoids to make use in the procedure of his knowledge of the solution (except in the end, where he needs to know the “step” in order to pick the solution that is aimed at among all the possible solutions). The numerical values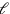 and
and
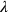 , the Babylonian needs to use identifications like “the length 30′” and “the length
, the Babylonian needs to use identifications like “the length 30′” and “the length
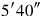 ” (both are lengths, so the name “length” without any qualifier will not suffice).
” (both are lengths, so the name “length” without any qualifier will not suffice).
Numerical values serve as identifiers in many texts; nonetheless, misunderstandings resulting from a mix-up of given and merely known numbers are extremely rare.
Footnotes
As in the case of “algebra” we shall pretend for the moment to know what an “equation” is. Analysis of the present text will soon allow us to understand in which sense the Old Babylonian problems can be understood as equations.
“you
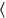 see
see
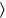 ” translates ta-
” translates ta-
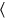 mar
mar
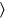 . The scribe thus does not omit a word, he uses the first syllable (which happens to carry the information about the grammatical person) as a logogram for the whole word. This is very common in the texts from Susa, and illustrates that the use of logograms is linked to the textual genre: only in mathematical texts can we be reasonably sure that no other verbs beginning with the syllable ta will be present in this position.
. The scribe thus does not omit a word, he uses the first syllable (which happens to carry the information about the grammatical person) as a logogram for the whole word. This is very common in the texts from Susa, and illustrates that the use of logograms is linked to the textual genre: only in mathematical texts can we be reasonably sure that no other verbs beginning with the syllable ta will be present in this position.
A right triangle is certainly also determined by a length and a width (the legs of the right angle), and these two magnitudes suffice to determine it (the third side, if it appears, may be “the long length”). But a triangle is always introduced as such. If it is not practically right, the text will give a sketch.
The word “practically” should be taken note of. The Babylonians had no concept of the angle as a measurable quantity—thus, nothing corresponding to our “angle of 78°.” But they distinguished clearly “good” from “bad” angles—we may use the pun that the opposite of a right angle was a wrong angle. A right angle is one whose legs determine an area—be it the legs of the right angle in a right triangle, the sides of a rectangle, or the height and the average base of a right trapezium.
“Simple” because there is also a “double false position” that may serve to solve more complex first-degree problems. It consists in making two hypotheses for the solution, which are then “mixed” (as in alloying problems) in such a way that the two errors cancel each other (in modern terms, this is a particular way to make a linear interpolation). Since the Babylonians never made use of this technique, a “false position” always refers to the “simple false position” in what follows.
The present document employs many logograms without phonetic or grammatical complements. Enough is written in syllabic Akkadian, however, to allow us to discern the usual scheme which, in consequence, is imposed upon the translation.
The Sumerian word é.dub.ba means “tablet house,” that is, “school.”