After these examples of first-degree methods we shall now go on with the principal part of Old Babylonian algebra—postponing once more the precise determination of what “algebra” will mean in a Babylonian context. In the present chapter we shall examine some simple problems, which will allow us to discover the fundamental techniques
BM 13901 #1
Obv. I
1The surface and my confrontation I have heaped: 45′ is it. 1, the projection,
2you posit. The moiety of 1 you break, 30′ and 30′ you make hold.
315′ to 45′ you join: by 1, 1 is equal. 30′ which you have made hold
4from the inside of 1 you tear out: 30′ the confrontation.
This is the problem that was quoted on page
Even though we know it well from this point of view, we shall once again examine the text and terminology in detail so as to be able to deal with it in the perspective of its author.
Line 1 states the problem
“Surface” and “confrontation” are heaped. This addition is the one that must be used when dissimilar magnitudes are involved, here an area (two dimensions) and a side (one dimension). The text tells the sum of the two magnitudes—that is, of their measuring numbers: 45′. If c stands for the side of the square and
 (c) for its area, the problem can thus be expressed in symbols in this way:
(c) for its area, the problem can thus be expressed in symbols in this way:
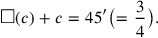
|

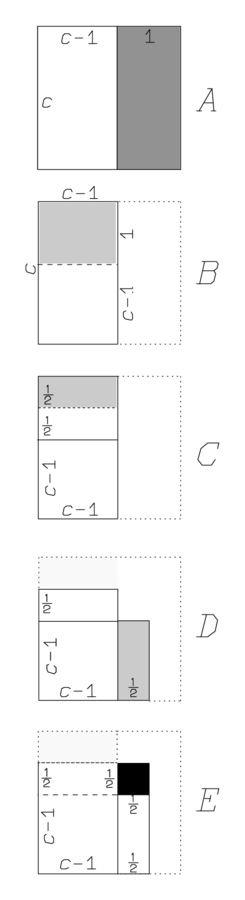
Fig. 3.1: The procedure of BM 13901 #1, in slightly distorted proportions.
Figure 3.1 shows the steps of the procedure leading to the solution as they are explained in the text:
A: 1, the projection, you posit. That means that a rectangle
 (c,1) is drawn alongside the square
(c,1) is drawn alongside the square
 (c). Thereby the sum of a length and an area, absurd in itself, is made geometrically meaningful, namely as a rectangular area
(c). Thereby the sum of a length and an area, absurd in itself, is made geometrically meaningful, namely as a rectangular area
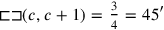 . This geometric interpretation explains the appearance of the “projection,”
. This geometric interpretation explains the appearance of the “projection,” (c,1)
“projects” from the square as a projection protruding from a building. We remember (see page
(c,1)
“projects” from the square as a projection protruding from a building. We remember (see page
B: The moiety of 1 you break. The “projection” with adjacent rectangle
 (c,1) is “broken” into two “natural” halves.
(c,1) is “broken” into two “natural” halves.
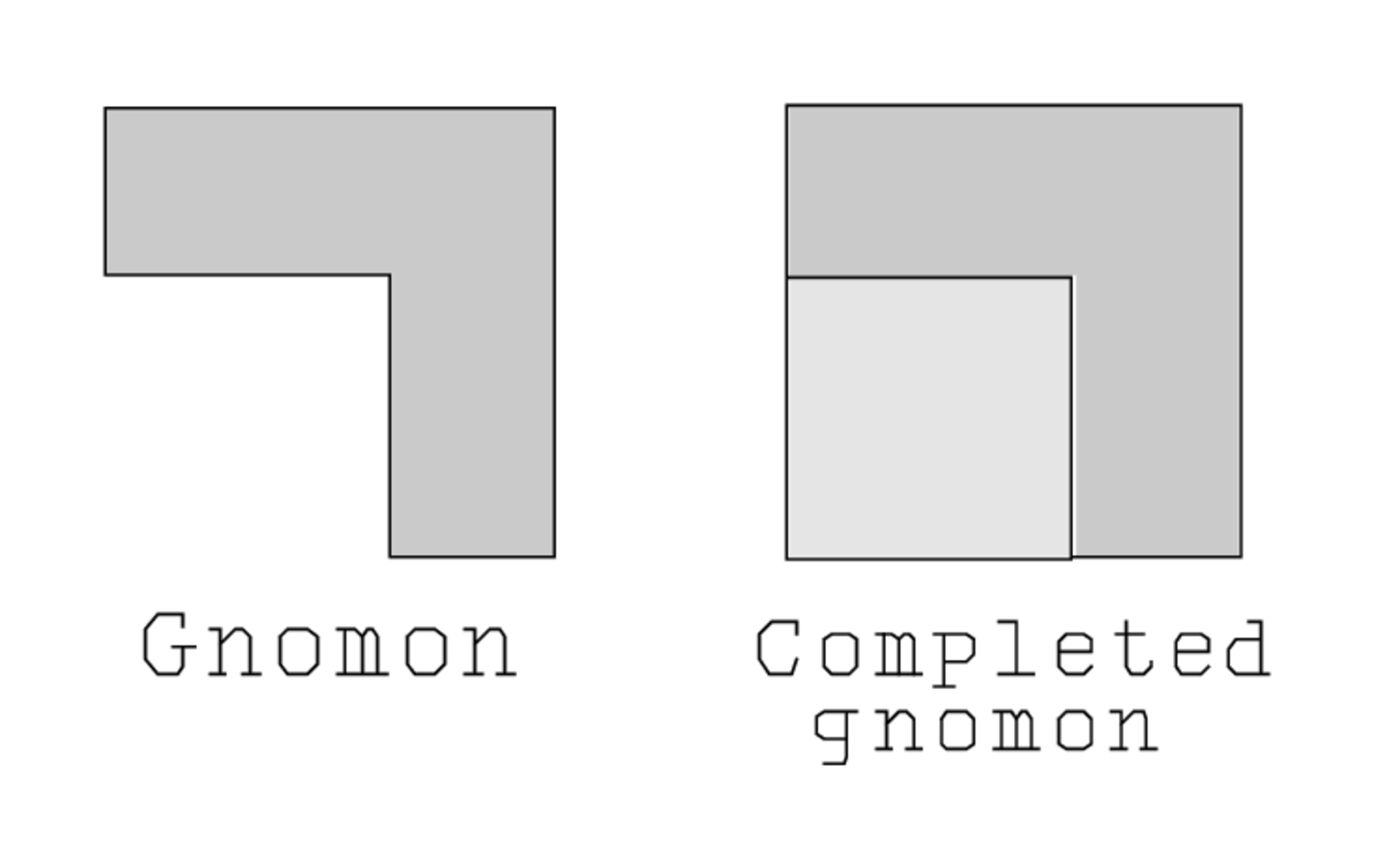
C: 30′ and 30′ you make hold. The outer half of the projection (shaded in grey) is moved around in such a way that its two parts (each of length 30′) “hold” the square with dotted border below to the left. This cut-and-paste (c,c+1) into a “gnomon,” a square from which a smaller square is lacking in a corner.
(c,c+1) into a “gnomon,” a square from which a smaller square is lacking in a corner.
D: 15′ to 45′ you join: 1. 15′ is the area of the square held by the two halves (30′ and 30′), and 45′ that of the gnomon. As we remember from page 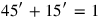 .
.
by 1, 1 is equal. In general, the phrase “by Q, s is equal” means (see page  as one of its equal sides (in arithmetical language,
as one of its equal sides (in arithmetical language,
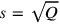 ). In the present case, the text thus tells us that the side of the completed square is 1, as indicated in D immediately to the left of the square.
). In the present case, the text thus tells us that the side of the completed square is 1, as indicated in D immediately to the left of the square.
30′ which you have made hold from the inside of 1 you tear out. of the original square we must now remove that piece of length
of the original square we must now remove that piece of length
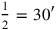 which was added to it below. To “tear out” a from H, as we have seen on page
which was added to it below. To “tear out” a from H, as we have seen on page
30′ the confrontation. Removing from 1 the segment
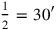 which was added, we get the initial side c, the “confrontation,” which is hence equal to
which was added, we get the initial side c, the “confrontation,” which is hence equal to
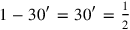 (extreme left in D).
(extreme left in D).
That solves the problem. In this geometric interpretation, not only the numbers are explained but also the words and explanations used in the text.
The new translation calls for some observation. We take note that no explicit argument is given that the cut-and-paste
The essential stratagem of the Old Babylonian method is the completion of the gnomon as shown in Figure 3.2. This stratagem is called a “quadratic completion”;
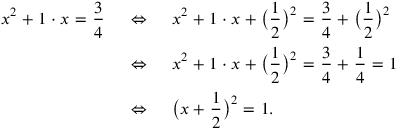
|
However, the name seems to apply even better to the geometric procedure.
It is obvious that a negative solution would make no sense in this concrete interpretation. Old Babylonian algebra was based on tangible quantities even in cases where its problems
Certain general expositions of the history of mathematics claim that the Babylonians did know of negative numbers. This is a legend based on sloppy reading. As mentioned, some texts state for reasons of style not that a magnitude A exceeds another one by the amount d but that B falls short of A by d; we shall encounter an example in BM 13901 #10 and
and
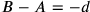
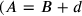 and
and
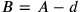 would have been closer to the ancient texts, but even Neugebauer had his reasons of style). In this way, mathematicians who only read the translations into formulas and not the explanations of the meaning of these (and certainly not the translated texts) found
would have been closer to the ancient texts, but even Neugebauer had his reasons of style). In this way, mathematicians who only read the translations into formulas and not the explanations of the meaning of these (and certainly not the translated texts) found
As the French Orientalist Léon Rodet wrote in 1881 when criticizing modernizing interpretations of an ancient Egyptian mathematical papyrus:
For studying the history of a science, just as when one wants to obtain something, ‘it is better to have business with God than with his saints’.1
BM 13901 #2
Obv. I
5My confrontation inside the surface I have torn out: 14‵30 is it. 1, the projection,
6you posit. The moiety of 1 you break, 30′ and 30′ you make hold,
715′ to 14‵30 you join: by 14‵30°15′, 29°30′ is equal.
830′ which you have made hold to 29°30′ you join: 30 the confrontation.
This problem, on a tablet which contains in total 24 problems of increasing sophistication dealing with one or more squares, follows immediately after the one we have just examined.
From the Old Babylonian point of view as well as ours, it is its “natural” counterpart. Where the preceding one “joins,”
Initially the problem is stated (line 5): My confrontation
To “tear out” (c,1), located inside the square. This rectangle (shaded in dark grey) must thus be “torn out”; what remains after we have eliminated
(c,1), located inside the square. This rectangle (shaded in dark grey) must thus be “torn out”; what remains after we have eliminated
 (c,1) from
(c,1) from
 (c) should be 14‵30. In modern symbols, the problem corresponds to
(c) should be 14‵30. In modern symbols, the problem corresponds to
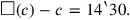
|
Once more, we are left with a rectangle for which we know the area (14‵30) and the difference between the length (
 ) and the width
) and the width
 —and once more, this difference amounts to 1, namely the “projection.”
—and once more, this difference amounts to 1, namely the “projection.”
1, the projection, you posit. In Figure 3.3, B, the rectangle
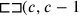 ) is composed of a (white) square and a (shaded) “excess” rectangle whose width is the projection 1.
) is composed of a (white) square and a (shaded) “excess” rectangle whose width is the projection 1.
The moiety of 1 you break. The excess rectangle, presented by its width 1, is divided into two “moieties”; the one which is detached is shaded in Figure 3.3, C.
Cutting and pasting this rectangle as seen in Figure 3.3, D we once again get a gnomon with the same area as the rectangle
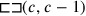 , that is, equal to 14‵30.
, that is, equal to 14‵30.
30′ and 30′ you make hold, 15′. The gnomon is completed with
the small square (black in Figure 3.3, E) which is “held” by the two
moieties. The area of this completing square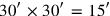 .
.
Next, the area of the completed square and its side are found: 15′ to 14‵30 you join: by 14‵30°15′, 29°30′ is equal.
Putting back the “moiety” which was moved around, we find the side of the initial square, which turns out to be 29°30′+30′ = 30: 30′ which you have made hold to 29°30′ you join: 30 the confrontation.
We notice that this time the “confrontation”
We also notice that the pair (14‵30°15′, 29°30′) does not appear in the table of squares and square roots (see page
YBC 6967
1The igibûm over the igûm, 7 it goes beyond
2igûm and igibûm what?
3You, 7 which the igibûm
4over the igûm goes beyond
5to two break: 3°30′;
63°30′ together with 3°30′
7make hold: 12°15′.
8To 12°15′ which comes up for you
91‵ the surface join: 1‵12°15′.
10The equal of 1‵12°15′ what? 8°30′.
118°30′ and 8°30′, its counterpart, lay down.
Rev.
13°30′, the made-hold,
2from one tear out,
3to one join.
4The first is 12, the second is 5.
512 is the igibûm, 5 is the igûm.
Second-degree problems
The above exercise belongs to the latter type—if we neglect the fact that it does not deal with a rectangle at all but with a pair of numbers belonging together in the table
One might expect the product of igûm and igibûm
It is important to notice that here the “fundamental representation”
As in the two analogous cases that precede, the rectangle is transformed into a gnomon, and as usually the gnomon is completed
The next steps are remarkable. The “moiety” that was detached and moved around (the “made-hold,” that is, that which was “made hold” the complementary square) in the formation of the gnomon is put back into place. Since it is the same piece which is concerned it must in principle be available before it can be “joined.” That has two consequences. Firstly, the “equal”
In BM 13901 #1
BM 13901 #10
Obv. II
11The surfaces of my two confrontations I have heaped: 21°15′.
12Confrontation (compared) to confrontation, the seventh it has become smaller.
137 and 6 you inscribe. 7 and 7 you make hold, 49.
146 and 6 you make hold, 36 and 49 you heap:
151‵25. igi 1‵25 is not detached. What to 1‵25
16may I posit which 21°15′ gives me? By 15′, 30′ is equal.
1730′ to 7 you raise: 3°30′ the first confrontation.
1830′ to 6 you raise: 3 the second confrontation.
We now return to the tablet containing a collection of problems and
and
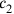 :
:
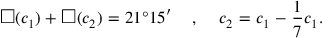
|
Formulated differently, the ratio between the two sides is as 7 to 6. This is the basis for a solution based on a “false position”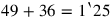 . According to the statement, however, the total should be 21°15′; therefore, the area must be reduced by a factor 21°15′/1‵25. Now 1‵25 is no “regular” number (see page
. According to the statement, however, the total should be 21°15′; therefore, the area must be reduced by a factor 21°15′/1‵25. Now 1‵25 is no “regular” number (see page 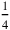 ). However, if the area is reduced by a factor 15′, then the corresponding sides must be reduced by a factor 30′: By 15′, 30′ is equal. It remains finally (lines 17 and 18) to “raise” 7 and 6 to 30′.
). However, if the area is reduced by a factor 15′, then the corresponding sides must be reduced by a factor 30′: By 15′, 30′ is equal. It remains finally (lines 17 and 18) to “raise” 7 and 6 to 30′.
The first “confrontation” thus turns out to be
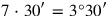 , and the second
, and the second
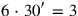 .5
.5
BM 13901 #14
Obv. II
44The surfaces of my two confrontations I have heaped:
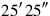 .
.
45The confrontation, two-thirds of the confrontation and 5′, nindan.
461 and 40′ and 5′ over-going 40′ you inscribe.
475′ and 5′ you make hold,
 inside
inside
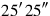 you tear out:
you tear out:
Rev. I
125′ you inscribe. 1 and 1 you make hold, 1. 40′ and 40′ you make hold,
2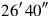 to 1 you join:
to 1 you join:
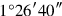 to 25′ you raise:
to 25′ you raise:
3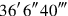 you inscribe. 5′ to 40′ you raise:
you inscribe. 5′ to 40′ you raise:
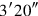
4and
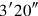 you make hold,
you make hold,
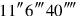 to
to
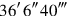 you join:
you join:
5by
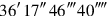 ,
,
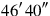 is equal.
is equal.
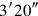 which you have made hold
which you have made hold
6inside
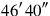 you tear out:
you tear out:
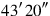 you inscribe.
you inscribe.
7igi
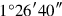 is not detached. What to
is not detached. What to
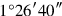
8may I posit which
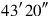 gives me? 30′ its bandûm.
gives me? 30′ its bandûm.
930′ to 1 you raise: 30′ the first confrontation.
1030′ to 40′ you raise: 20′, and 5′ you join:
1125′ the second confrontation.
Even this problem deals with two squares (lines Obv. II.44–45).6 The somewhat obscure formulation in line 45 means that the second “confrontation” equals two-thirds of the first, with additional 5′ nindan. If
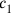 and
and
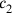 stands for the two “confrontations,” line 44 informs us that the sum of the areas is
stands for the two “confrontations,” line 44 informs us that the sum of the areas is
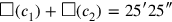 , while line 45 states that
, while line 45 states that
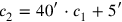 .
.
This problem cannot be solved by means of a simple false position in which a hypothetical number is provisionally assumed as the value of the unknown—that only works for homogeneous problems.7 The numbers 1 and 40′ in line 46 show us the way that is actually chosen:
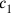 and
and
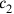 are expressed in terms of a new magnitude, which we may call
are expressed in terms of a new magnitude, which we may call
 :
:

|
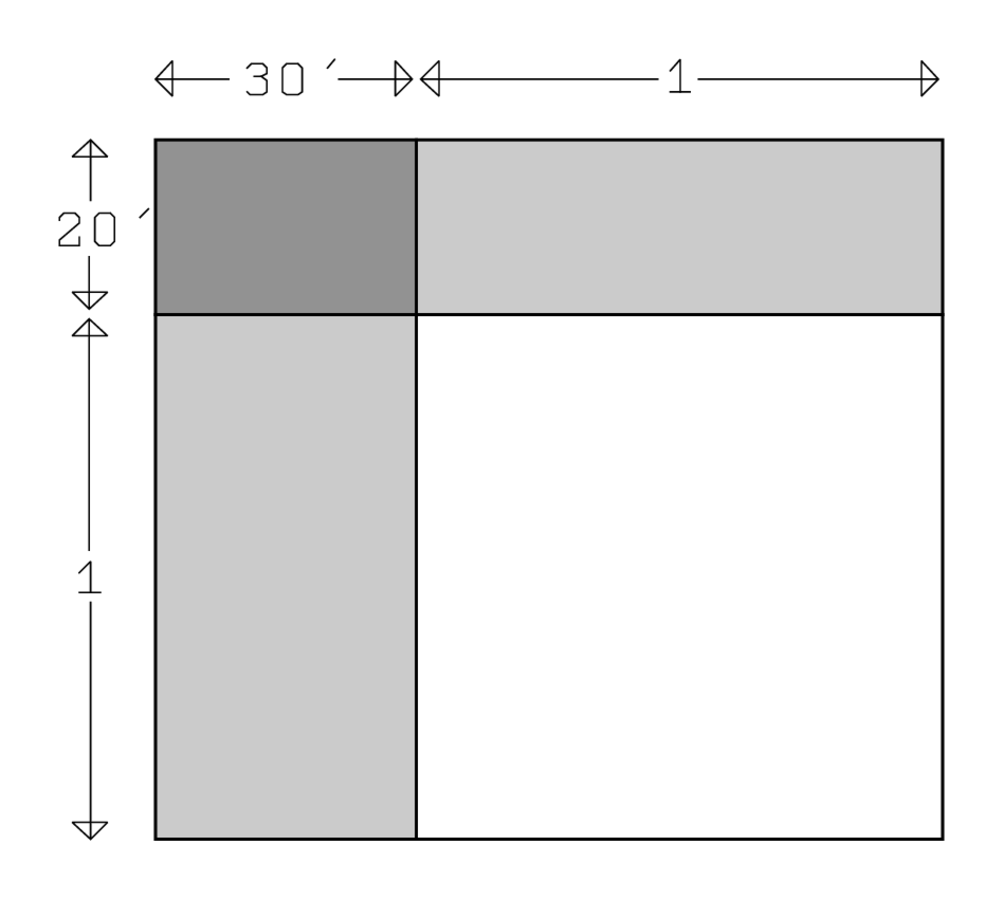
That corresponds to Figure 3.6. It shows how the problem is reduced to a simpler one dealing with a single square
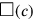 . It is clear that the area of the first of the two original squares (
. It is clear that the area of the first of the two original squares (
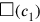 ) equals
) equals
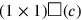 , but that calculation has to wait until line Rev. I.1. The text begins by considering
, but that calculation has to wait until line Rev. I.1. The text begins by considering
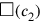 , which is more complicated and gives rise to several contributions. First, the square
, which is more complicated and gives rise to several contributions. First, the square
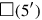 in the lower right corner: 5′ and 5′ you make hold,
in the lower right corner: 5′ and 5′ you make hold,
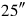 . This contribution is eliminated from the sum
. This contribution is eliminated from the sum
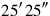 of the two areas:
of the two areas:
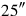 inside
inside
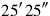 you tear out: 25′ you inscribe. The 25′ that remains must now be explained in terms of the area and the side of the new square
you tear out: 25′ you inscribe. The 25′ that remains must now be explained in terms of the area and the side of the new square
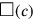 .
.
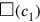 , as already said, is
, as already said, is
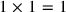 times the area
times the area
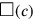 : 1 and 1 you make hold, 1.8 After elimination of the corner
: 1 and 1 you make hold, 1.8 After elimination of the corner
 remains of
remains of
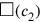 , on one hand, a square
, on one hand, a square
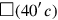 , on the other, two “wings” to which we shall return imminently. The area of the square
, on the other, two “wings” to which we shall return imminently. The area of the square
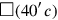 is
is
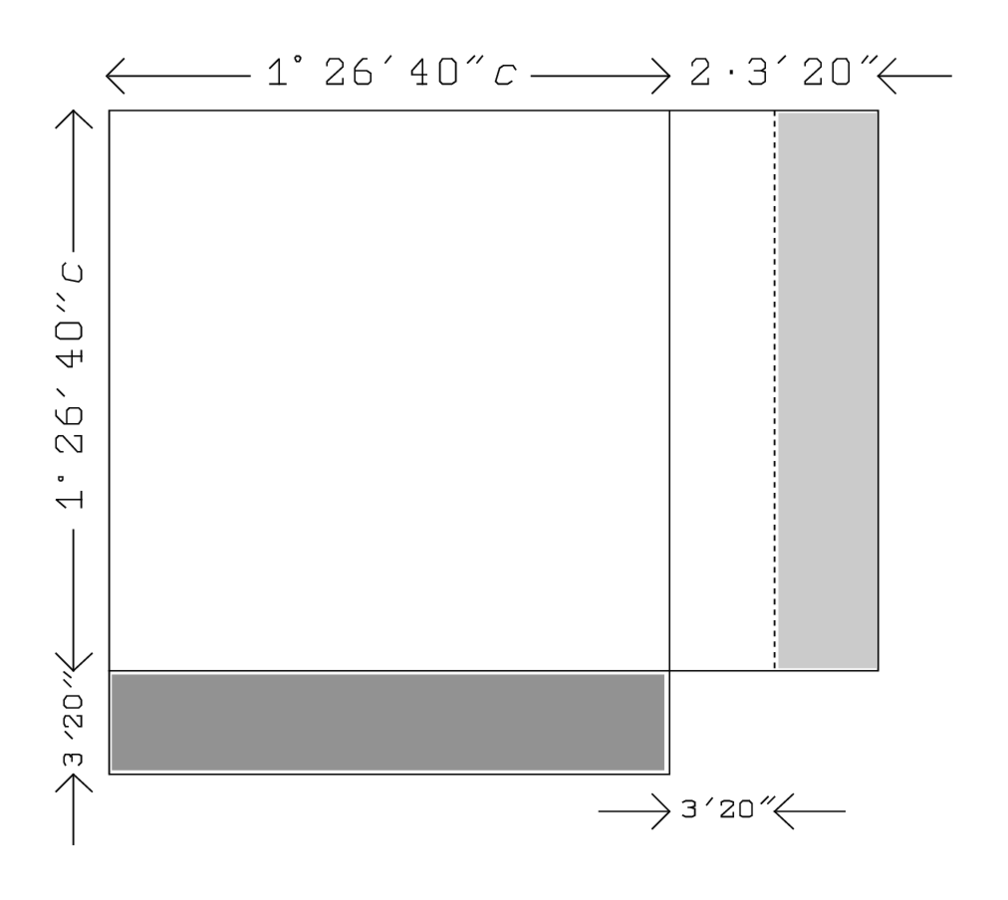
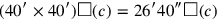 : 40′ and 40′ you make hold, 26′40″. In total we thus have
: 40′ and 40′ you make hold, 26′40″. In total we thus have
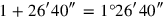 times the square area
times the square area
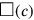 : 26′40″ to 1 you join: 1°26′40″.
: 26′40″ to 1 you join: 1°26′40″.
Each “wing” is a rectangle
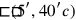 , whose area can be written
, whose area can be written
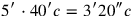 : 5′ to 40′ you raise: 3′20″.
: 5′ to 40′ you raise: 3′20″.
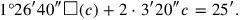
|
This equation confronts us with a problem which the Old Babylonian author has already foreseen in line Rev. I.2, and which has caused him to postpone until later the calculation of the wings. In modern terms, the equation is not “normalized,” that is, the coefficient of the second-degree term differs from 1. The Old Babylonian calculator might correspondingly have explained it by stating in the terminology of TMS XVI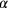 square areas (the white rectangle
square areas (the white rectangle
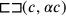 ) and
) and
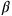 sides, that is, the shaded rectangle
sides, that is, the shaded rectangle
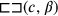 , corresponding to the equation
, corresponding to the equation
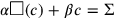
|
(in the actual case,
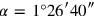 ,
,
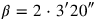 ,
,
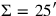 ). This prevents us from using directly our familiar cut-and-paste
). This prevents us from using directly our familiar cut-and-paste and making the two “moieties” “hold” would not give us a gnomon.
and making the two “moieties” “hold” would not give us a gnomon.
The Babylonians got around the difficulty by means of a device shown in the right-hand side of figure 3.7: the scale instead of
instead of
 ; in consequence the sum of the two areas is no longer
; in consequence the sum of the two areas is no longer
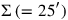 but
but
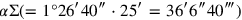 :
:
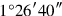 to 25′ you raise:
to 25′ you raise:
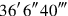 you inscribe. As we see, the number
you inscribe. As we see, the number
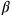 of sides is not changed in the operation, only the value of the side, namely from
of sides is not changed in the operation, only the value of the side, namely from
 into
into
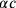 .9
.9
In modern symbolic language, this transformation corresponds to a multiplication of the two sides of the equation
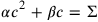
|
by
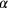 , which gives us a normalized equation with the unknown
, which gives us a normalized equation with the unknown
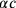 :
:
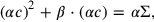
|
an equation of the type we have encountered in BM 13901 #1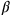 ). As already said, each “wing” contributes
). As already said, each “wing” contributes
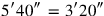 sides. If the calculator had worked mechanically, according to fixed algorithms, he would now have multiplied by 2 in order to find
sides. If the calculator had worked mechanically, according to fixed algorithms, he would now have multiplied by 2 in order to find
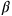 . But he does not! He knows indeed that the two wings constitute the excess that has to be “broken” into
two “moieties.” He therefore directly makes
. But he does not! He knows indeed that the two wings constitute the excess that has to be “broken” into
two “moieties.” He therefore directly makes
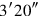 and
and
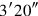 “hold,” which produces the quadratic complement, and “joins” the resulting area
“hold,” which produces the quadratic complement, and “joins” the resulting area
 to that of the gnomon
to that of the gnomon
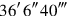 :
:
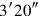 and
and
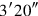 you make hold,
you make hold,
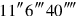 to
to
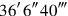 you join: […]
you join: […]
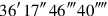 .
.
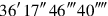 is thus the area of the completed
is thus the area of the completed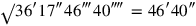 : by
: by
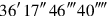 ,
,
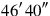 is equal. This number represents
is equal. This number represents
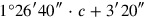 ; therefore,
; therefore,
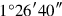
 is
is
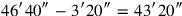 :
:
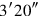 which you have made hold inside
which you have made hold inside
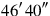 you tear out:
you tear out:
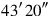 you inscribe. Next, we must find the value of c.
you inscribe. Next, we must find the value of c.
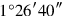 is an irregular number, and the quotient
is an irregular number, and the quotient
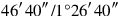 is given directly as 30′:10 igi
is given directly as 30′:10 igi
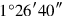 is not detached. What to
is not detached. What to
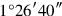 may I posit which
may I posit which
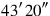 gives me? 30′ its bandûm.
gives me? 30′ its bandûm.
In the end,
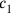 and
and
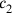 are determined,
are determined,
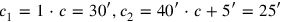 :11 30′ to 1 you raise: 30′ the first confrontation. 30′ to 40′ you raise: 20′, and 5′ you join: 25′ the second confrontation.
The problem is solved.
:11 30′ to 1 you raise: 30′ the first confrontation. 30′ to 40′ you raise: 20′, and 5′ you join: 25′ the second confrontation.
The problem is solved.
TMS IX #1 and #2
#1
1The surface and 1 length I have heaped, 40′. ¿30, the length,? 20′ the width.
2As 1 length to 10′ the surface, has been joined,
3or 1 (as) base to 20′, the width, has been joined,
4or 1°20′ ¿is posited? to the width which 40′ together with the length ¿holds?
5or 1°20′ toge
 ther
ther
 with 30′ the length holds, 40′ (is) its name.
with 30′ the length holds, 40′ (is) its name.
6Since so, to 20′ the width, which is said to you,
71 is joined: 1°20′ you see. Out from here
8you ask. 40′ the surface, 1°20′ the width, the length what?
930′ the length. Thus the procedure.
#2
10Surface, length, and width I have heaped, 1. By the Akkadian (method).
111 to the length join. 1 to the width join. Since 1 to the length is joined,
121 to the width is joined, 1 and 1 make hold, 1 you see.
131 to the heap of length, width and surface join, 2 you see.
14To 20′ the width, 1 join, 1°20′. To 30′ the length, 1 join, 1°30′.
15¿Since? a surface, that of 1°20′ the width, that of 1°30′ the length,
16¿the length together with? the width, are made hold, what is its name?
172 the surface.
18Thus the Akkadian (method).
As TMS XVI #1
Figure (3.9) is drawn in agreement with the text of #1, in which the sum of a rectangular area and the corresponding length is known. In parallel with our symbolic transformation
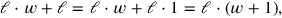
|
the width is extended by a “base.”
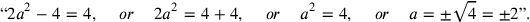
|
Line 2 speaks of the “surface” as 10′. This shows that the student is once more supposed to know that the discussion deals with the rectangle
 (30′,20′). The tablet is broken, for which reason we cannot know whether the length was stated explicitly, but the quotation in line 6 shows that the width was.
(30′,20′). The tablet is broken, for which reason we cannot know whether the length was stated explicitly, but the quotation in line 6 shows that the width was.
In the end, lines 7–9 shows how to find the length once the width is known together with the sum of area and length (by means of a division that remains implicit).
#2 teaches how to confront a more complex situation; now the sum of the area and both sides is given (see Figure 3.10). Both length and width are prolonged by 1; that produces two rectangles
 (
(
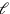 ,1) and
,1) and
 (
(
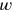 ,1), whose areas, respectively, are the length and the width. But it also produces an empty square corner
,1), whose areas, respectively, are the length and the width. But it also produces an empty square corner
 (1,1). When it is filled we have a larger rectangle of length
(1,1). When it is filled we have a larger rectangle of length
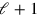 (= 1°30′), width
(= 1°30′), width
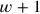 (= 1°20′) and area
(= 1°20′) and area
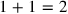 ; a check confirms that the rectangle “held” by these two sides is effectively of area 2.
; a check confirms that the rectangle “held” by these two sides is effectively of area 2.
This method has a name, which is very rare in Old Babylonian mathematics (or at least in its written traces). It is called “the Akkadian (method).”
Footnotes
Léon Rodet, Journal asiatique, septième série 18, p. 205.
The inverse of the “heaping” operation, on the other hand, is no subtraction at all but a separation into constitutive elements. See note 3, page
The verb in question (nadûm) has a broad spectrum of meanings. Among these are “to draw” or “to write” (on a tablet) (by the way, the word lapātum, translated “to inscribe,” has the same two meanings). Since what is “laid down” is a numerical value, the latter interpretation could seem to be preferable—but since geometrical entities were regularly identified by means of their numerical measure, this conclusion is not compulsory.
Here we see one of the stylistic reasons that would lead to a formulation in terms of falling-short instead of excess. It might as well have been said that one side exceeds the other by one sixth, but in the “multiplicative-partitive” domain the Babylonians gave special status to the numbers 4, 7, 11, 13, 14 and 17. In the next problem on the tablet, one “confrontation” is stated to exceed the other by one seventh, while it would be just as possible to say that the second falls short of the first by one eighth.
One might believe the underlying idea to be slightly different, and suppose that the original squares are subdivided into 7
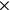 7 respectively 6
7 respectively 6
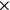 6 smaller squares, of which the total number would be 1‵25, each thus having an area equal to
6 smaller squares, of which the total number would be 1‵25, each thus having an area equal to
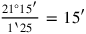 and a side of 30′. However, this interpretation is ruled out by the use of the operation “to make hold”: Indeed, the initial squares are already there, and there is thus no need to construct them (in TMS VIII #1 we shall encounter a subdivision into smaller squares, and there their number is indeed found by “raising”—see page
and a side of 30′. However, this interpretation is ruled out by the use of the operation “to make hold”: Indeed, the initial squares are already there, and there is thus no need to construct them (in TMS VIII #1 we shall encounter a subdivision into smaller squares, and there their number is indeed found by “raising”—see page
This part of the tablet is heavily damaged. However, #24 of the same tablet, dealing with three squares but otherwise strictly parallel, allows an unquestionable reconstruction.
In a simple false position, indeed, the provisionally assumed number has to be reduced by a factor corresponding to the error that is found; but if we reduce values assumed for
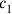 and
and
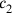 with a certain factor—say,
with a certain factor—say,
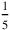 —then the additional 5′ would be reduced by the same factor, that is, to 1′. After reduction we would therefore have
—then the additional 5′ would be reduced by the same factor, that is, to 1′. After reduction we would therefore have
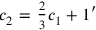 .
.
This meticulous calculation shows that the author thinks of a new square, and does not express
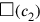 in terms of
in terms of
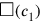 and
and
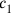 .
.
This device was used
constantly in the solution of non-normalized problems, and there is no reason to suppose that the Babylonians needed a specific representation similar to Figure 3.7. They might imagine that the measuring scale was changed in one direction—we know from other texts that their diagrams could be very rough, mere structure diagrams—nothing more than was required in order to guide thought. All they needed was thus to multiply the sum
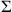 by
by
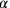 , and that they could (and like here, would) do before calculating
, and that they could (and like here, would) do before calculating
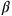 .
.
The quotient is called ba.an.da. This Sumerian term could mean “that which is put at the side,” which would correspond to way multiplications were performed on a tablet for rough work, cf. note 11, page
That the value of c1 is calculated as 1⋅c and not directly identified with c confirms that we have been working with a new side c.
The tablet is rather damaged; as we remember, passages in ¿…? are reconstructions that render the meaning (which can be derived from the context) but not necessarily the exact words of the original.
The word ki.gub.gub is a composite Sumerian term that is not known from elsewhere and which could be an ad hoc construction. It appears to designate something stably placed on the ground.


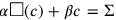 .
.