One way to explain socio-cultural structures and circumstances argues from their function: if the scribe school
Another way to explain them—no alternative but rather the other side of the coin—is based on historical origin
Over the last 40 years, our knowledge about Mesopotamian third-millennium mathematics has advanced much, in particular concerning the determination of rectangular or quasi-rectangular areas. We may now confidently assert that the reason that we have found no third-millennium texts containing algebra problems is that there were none.
This contradicts the traditional belief that everything in Mesopotamia must date from times immemorial. Certainly, we are in the “Orient”
The Origin: Surveyors’ Riddles
On the contrary, the algebra of the Old Babylonian scribe school is no continuation of century- (or millennium-)old school traditions—nothing similar had existed during the third millennium. It is one expression among others of the new scribal culture of the epoch
However, an invention within the scribe school agrees very badly with other sources. In particular it is in conflict with the way problems and techniques belonging to the same family turn up in Greek and medieval sources. A precise analysis of all parallel material reveals a very different story—the material is much too vast to allow a complete presentation of the argument here, but part of it is woven into the following discussion.
The surveyors of central Iraq (perhaps a wider region, but that remains a hypothesis in as far as this early epoch is concerned) had a tradition of geometrical riddles
Somebody goes to the market and buys 100 fowls for 100 dinars. A goose costs him 3 dinars, a hen 2 dinars, and of sparrows he gets 3 for each dinar. Tell me, if you are an expert calculator, what he bought!1
There are many solutions. 5 geese, 32 hens, and 63 sparrows; 10 geese, 24 hens, and 66 sparrows; etc. However, when answering a riddle, even a mathematical riddle
Often the solution of a similar riddle asks for the application of a particular trick. Here, for instance, one may notice that one must buy 3 sparrows each time one buys a goose—that gives 4 fowls for 4 dinars—and 3 sparrows for each two hens—5 fowls for 5 dinars.
Such “recreational problems”
At some moment between 2200 and 1800 bce , the Akkadian surveyors invented the trick that was later called “the Akkadian method,” that is, the quadratic completion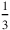 of the area.” We may say that the problems are defined without coefficients, of, alternatively, with “natural” coefficients.
of the area.” We may say that the problems are defined without coefficients, of, alternatively, with “natural” coefficients.
If
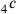 stands for “the 4 sides” and
stands for “the 4 sides” and
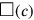 for the area of a square,
for the area of a square,
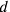 for the diagonal and
for the diagonal and
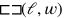 for the area of a rectangle, the list of riddles
for the area of a rectangle, the list of riddles
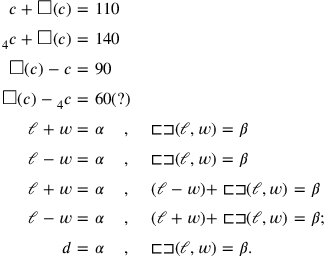
|
Beyond that, there were problems concerning a square, with the pseudo-solution
concerning a square, with the pseudo-solution
 ,
,
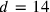 ; two problems about a rectangle
; two problems about a rectangle
These riddles appear to have been adopted into the Old Babylonian scribe school
Such considerations explain why a problem collection about squares like BM 13901
On the other hand, as a consequence of the drill of systematic variation, the solution of the fundamental problems became a banality on which professional self-esteem could not be built: thereby work on complicated problems became not only a possibility but also a cultural necessity.
One may assume that the orientation of the scribal profession toward a wide range of practices invited the invention of problems outside abstract surveying geometry where the algebraic methods could be deployed—and therefore, even though “research” was no aim of the scribal school, to explore the possibilities of representation. It is thus, according to this reconstruction, the transfer to the school that gave to the cut-and-paste
Other changes were less momentous though still conspicuous. In the riddles, 10 was the preferred value for the side of the square, remaining so until the sixteenth century ce; the favorite value in school was 30′, and when an archaizing problem retained 10 it was interpreted as 10′.5 Finally, as explained above (page
BM 13901 #23
It appears that the first development of the algebraic discipline took place in the Eshnunna region, north of Babylon, during the early decades of the eighteenth century;6 from this area and period we have a number of mathematical texts that for once have been regularly excavated and which can therefore be dated. By then, Eshnunna was a cultural centre of the whole north-central part of Iraq; Eshnunna also produced the first law-code outside the Sumerian south. The text Db2–146 (below, page
In c. 1761 Eshnunna was conquered by Hammurabi and destroyed. We know that Hammurabi borrowed the idea of a law-code, and can assume that he brought enslaved scholars back. Whether he also brought scholars engaged in the production or teaching of mathematics is nothing but a guess (the second-millennium strata of Babylon are deeply buried below the remains of the first-millennium world city), but in any case the former Sumerian south took up the new mathematical discipline around 1750—AO 8862
Problems from various sites in the Eshnunna region deal with many of the topics also known from later—the early rectangle variant of the “broken-reed” problem mentioned on page
Not much later, we have a number of texts which (to judge from their orthography) were written in the south. Several text groups obey very well-defined canons for format and terminology (not the same in all groups), demonstrating a conscious striving for regularity (the VAT- and Str-texts all belong here). However, around 1720 the whole south seceded, after which scribal culture there was reduced to a minimum; mathematics seems not to have survived. From the late seventeenth century, we have a fair number of texts from Sippar, somewhat to the north of Babylon (BM 85200+VAT 6599 is one of them), and another batch from Susa in western Iran (the TMS-texts), which according to their terminology descend from the northern type first developed in Eshnunna. And then, nothing more … .
The Heritage
Indeed, in 1595 a Hittite
The scribe school
Even sophisticated mathematics disappeared. The social need for practical calculation, though reduced
The 1200 years that follow the collapse of the Old Babylonian cultural complex have not left a single algebra text. In itself that does not say much, since only a very small number of mathematical texts even in the vaguest sense have survived (a few accounting texts, traces of surveying, some tables of reciprocals
These late texts obviously do not inform us, neither directly nor indirectly, about the environment where the riddles had been transmitted, even though a continuation of the surveyors’ tradition is the most verisimilar hypothesis. Sources from classical antiquity as well as the Islamic Middle Ages at least make it clear that the tradition that had once inspired Old Babylonian algebra had survived despite the disappearance of its high-level offspring.
The best evidence is offered by an Arabic manual of practical geometry
In Greek as “four feet.”
as “four feet.”
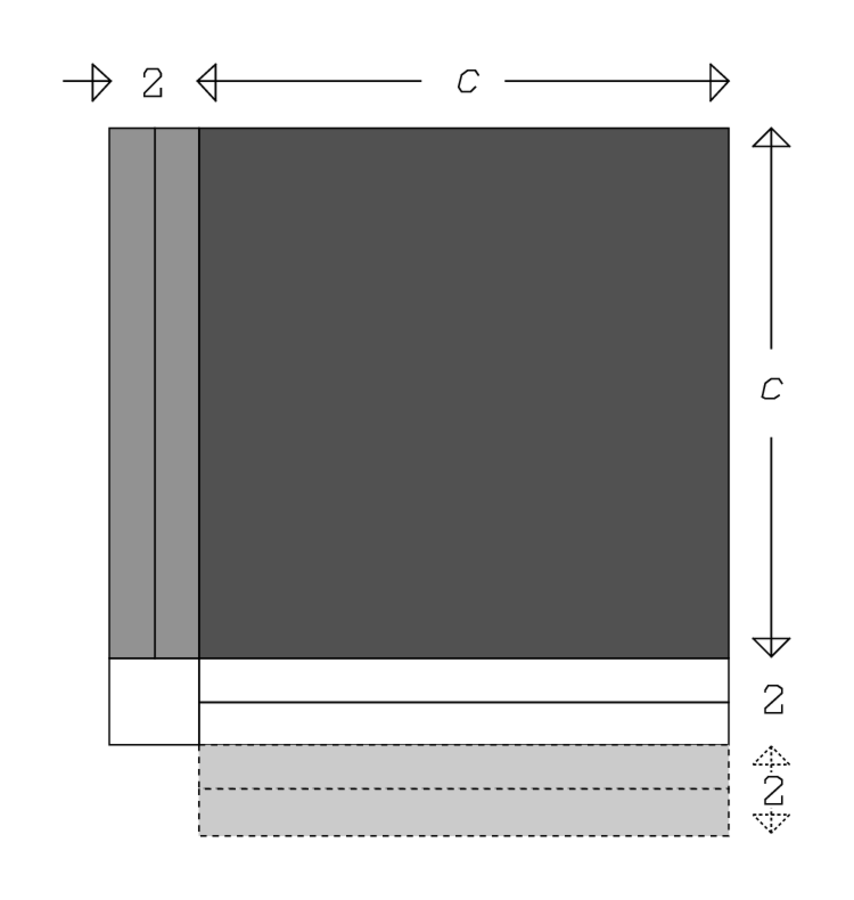
Fig. 8.1: “The area joined to the perimeter” of Geometrica.
Since the discovery of Babylonian algebra, it has often been claimed that one component of Greek theoretical geometry (namely, Euclid’s Elements
However, if we align the ten theorems Elements II.1–10 with the list of original riddles we make an unexpected discovery: all ten theorems can be connected directly to the list—they are indeed demonstrations that the naive methods of the riddle tradition can be justified according to the best theoretical standards of Euclid’s days.
The extraordinary importance of the Elements in the history of mathematics is beyond doubt. None the less, the most important influence of the surveyors’ tradition in modern mathematics is due to its interaction with medieval Arabic algebra
Even Arabic algebra seems to have originally
you halve the roots, which in this question are 5. You then multiply them with themselves, from which arises 25; add them to 39, and they will be 64. You should take the root of this, which is 8. Next remove from it the half of the roots, which is 5. Then 3 remains, which is the root of the possession. And the possession is 9.
Already the first author of a treatise on algebra which we know (which is probably the first treatise about the topic8)—al-Khwārizmī
Thus, even though the algebra of the cuneiform tablets was a blind alley—glorious but blind all the same—the principles that it had borrowed from practitioners without erudition was not. Without this inspiration it is difficult to see how modern mathematics
Footnotes
This is an “average” variant. The prices may vary, and also the species (mostly but not always birds are traded). As a rule, however, the problem speaks about 100 animals and 100 monetary units. There are mostly three species, two of which cost more than one unit while the third costs less.
Who wants to, can try to find the full solution with or without negative numbers (which would stand for selling instead of buying), and demonstrate that it does represent an exhaustive solution under the given circumstances. That was done by the Arabic mathematician Abū Kāmil around 900 ce. In the introduction to his treatise about the topic he took the opportunity to mock those practitioners deprived of theoretical insight who gave an arbitrary answer only—and who thus understood the question as a riddle and not as a mathematical problem.
In the Old Babylonian texts, a closed group consisted of the four rectangle problems where the area is given together with the length; the width; the sum of these; or their difference. One may presume that the completion trick was first invented as a way to make this group grow from two to four members.
Who only practices equation algebra for the sake of finding solutions may not think much of coefficients—after all, they are mostly a nuisance to be eliminated. However, Viète and his generation made possible the unfolding of algebraic theory in the seventeenth century by introducing the use of general symbols for the coefficients. Correspondingly, the Old Babylonian teachers, when introducing coefficients, made possible the development of algebraic practice—without the availability and standardized manipulation of coefficients, no free representation is possible.
In order to see that 10 (and 30) had precisely this role one has to show that 10 was not the normal choice in other situations where a parameter was chosen freely. Collation of many sources shows that 10 (respectively 30 in descendants of the school tradition) was the preferred side not only of squares but also of other regular polygons—just as 4, 7, 11, etc. can be seen to have been favorite numbers in the multiplicative-partitive domain but only there, cf. note 4, page
Eshnunna had been subdued by Ur III in 2075 but broke loose already in 2025.
The Liber mensurationum ascribed to an unidentified Abū Bakr “who is called Heus” and translated by Gerard of Cremona.
The quotation is borrowed from this treatise, rendered in “conformal translation” of the Latin twelfth-century version (the best witness of the original wording of the text).
