Abstract. Entanglement—according to Schrödinger 1935 the essential property of quantum mechanics—teaches us that the properties of individual quantum systems cannot be considered to be (local) elements of physical reality before and independent of observation. Yet it is a widespread point of view that the way the observations on, say, two particles are correlated, i.e. the specific type of their entanglement, can still be considered as a property of the physical world. Here I discuss a previous experiment Walther et.al. 2006 showing that this is explicitly not the case. The correlations between a single particle property, the polarization state of a photon, and a joint property of two particles, the entangled state of a photon pair in a three-photon entangled state, have been measured. It is shown that the correlations between these properties can obey a cosine relation in direct analogy with the polarization correlations in one of the triplet Bell states Bell 1964. The cosine correlations between the polarization and entangled state measurements are too strong for any local-realistic explanation and are experimentally exploited to violate a Clauser-Horne-Shimony-Holt (CHSH) Bell inequality Bell 1964. Thus, entanglement itself can be an entangled property leading to the notion of entangled entanglement.
1 Introduction
In general, quantum mechanics only makes probabilistic predictions for individual events. Can one go beyond quantum mechanics in this respect? More than seventy years ago, in 1935, Einstein, Podolsky and Rosen (EPR) argued that quantum theory could not possibly be complete Einstein et.al. 1935. They showed that one could infer perfectly complementary properties, like position and momentum of an individual particle, by performing a corresponding measurement on the distant particle that is quantum-mechanically entangled with the first one. Based firmly on plausible assumptions about locality, realism, and theoretical completeness, they further argued that quantum states cannot be a complete description of physical reality, but rather give only a statistical one of an ensemble of intrinsically different quantum systems. While at the time, Bohr 1935 famously argued against EPRís conclusions, in particular against their notion of “reality” as assuming the systems have intrinsic properties independently of whether they are observed or not, it was not until almost 30 years later that the EPR program could be formulated in terms of an experimentally-testable prediction. I am, of course, referring to the landmark discovery of John Bell 1964 that EPRís premises of locality and realism put measurable limits on the strength of correlations between outcomes of remote measurements on a pair of systems. These limits are known as Bell inequalities and quantum mechanics does not satisfy them.
Since Bell's initial discovery, a large volume of theoretical and experimental work has been devoted to this subject. Experimental violations of Bell inequalities have been demonstrated using pairs of polarization-entangled photons Bell 1964, even under strict Einstein locality requirement, using other photonic degrees of freedom such as energy-time Bell 1964 and angular momentum Vaziri et.al. 2002, trapped ions Rowe et.al. 2001, and even neutron systems Hasegawa et.al. 2004. Multiphoton entanglement experiments have been performed demonstrating all-versus-nothing arguments against local realism Pan et.al. 2000 by exploiting so-called Greenberger-Horne-Zeilinger (GHZ) states Greenberger et.al. 1989, where single measurement outcomes can be incompatible with local realistic models. Aside from outstanding loopholes, which have not all been closed simultaneously in a single experiment Greenberger et.al. 1989, these experiments all but rule out the possibility of local realistic theories. However, common to all previous Bell experiments, regardless of the implementation, is that the measured degrees of freedom corresponded to properties of individual systems. Entanglement itself, as a property of the composite systems, was usually considered an objective property.
The experiment discussed in the following, however, demonstrated the first example of a Bell-inequality violation where an entangled state itself qualifies as an EPR element of reality. Specifically, a measurement of the single particle at Alice's side defines the relational property between the two other particles, without defining their single-particle properties. Therefore, only the joint state of the two qubits at Bob's side is an element of reality. The correlations between the polarization state of one photon and the entangled state of another two are experimentally demonstrated to violate the Bell inequality. This shows that entanglement itself can be entangled. The notion that entanglement itself can be an entangled property was originally proposed in the context of Greenberger et.al. 1989.
2 An Experiment on Entangled Entanglement
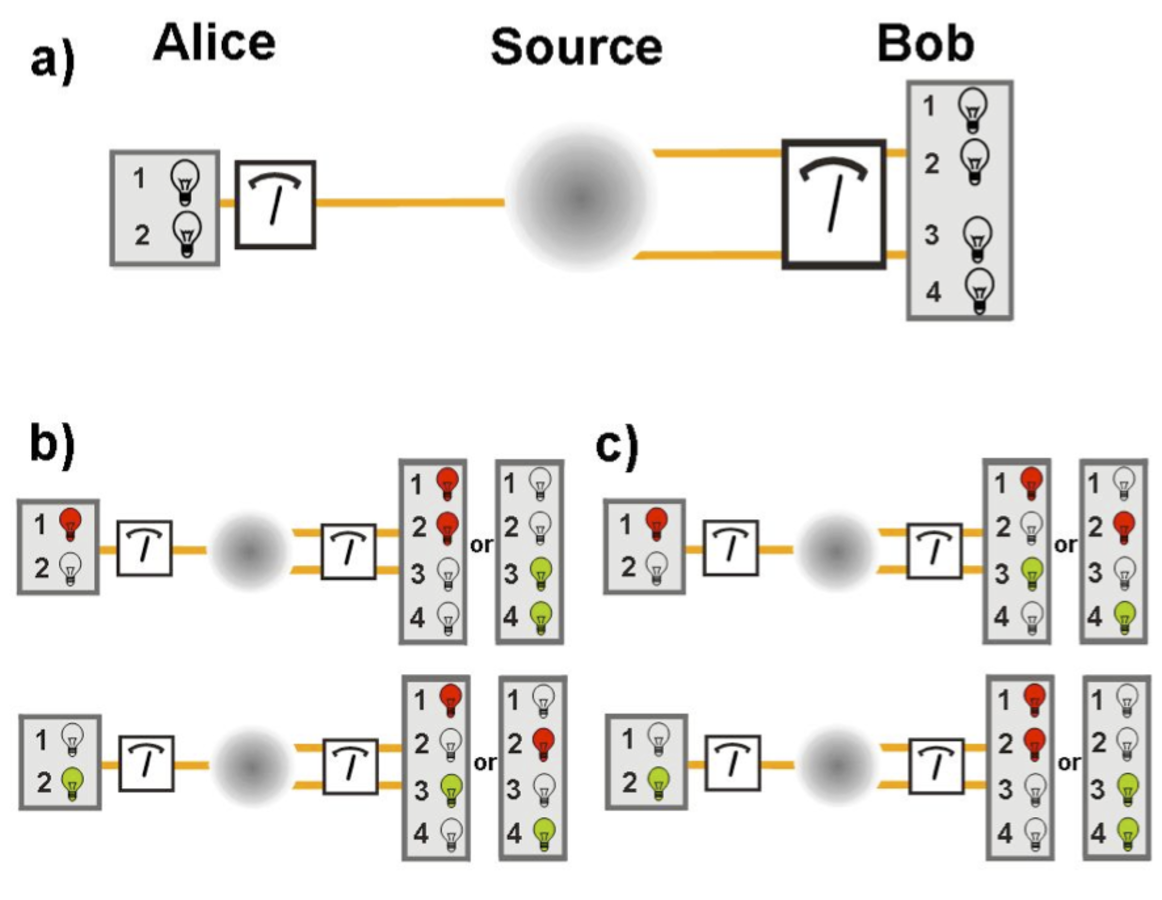
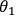 , of the analyzer, the measurement outcome is
+1 (red light bulb) or -1 (green light bulb) when perpendicular. In contrast, Bob makes
projective measurements onto a two-particle entangled state, where again the orientation
of the apparatus is defined by the angle,
, of the analyzer, the measurement outcome is
+1 (red light bulb) or -1 (green light bulb) when perpendicular. In contrast, Bob makes
projective measurements onto a two-particle entangled state, where again the orientation
of the apparatus is defined by the angle,
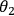 . Bobís outcomes are defined as +1, when
detectors 1 & 2 (red light bulbs) or 3 & 4 (green light bulbs) are firing, or -1 when
detectors 1 & 3 or 2 & 4 are firing. b) When Alice and Bob measure with the same
measurement settings, i.e.
. Bobís outcomes are defined as +1, when
detectors 1 & 2 (red light bulbs) or 3 & 4 (green light bulbs) are firing, or -1 when
detectors 1 & 3 or 2 & 4 are firing. b) When Alice and Bob measure with the same
measurement settings, i.e.
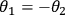 , they observe perfect correlations, which appear in
four possible configurations, given by +1. However, when they measure in a different
basis, i.e.
, they observe perfect correlations, which appear in
four possible configurations, given by +1. However, when they measure in a different
basis, i.e.
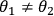 , they will also observe four possible anti-correlations c), given by
-1. The correlation measurements with different measurement settings form the basis of a
test of local realism using entangled entanglement.
, they will also observe four possible anti-correlations c), given by
-1. The correlation measurements with different measurement settings form the basis of a
test of local realism using entangled entanglement.Fig. 1: Schematic for the Bell experiment based on an entangled entangled state.
a) A source emits three entangled photons in such a way that one photon is received by
Alice and the two other photons by Bob. Alice controls an analyzer that makes
measurements of the polarization of her photon. When the photonís polarization is
measured to be parallel to orientation,
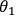 , of the analyzer, the measurement outcome is
+1 (red light bulb) or -1 (green light bulb) when perpendicular. In contrast, Bob makes
projective measurements onto a two-particle entangled state, where again the orientation
of the apparatus is defined by the angle,
, of the analyzer, the measurement outcome is
+1 (red light bulb) or -1 (green light bulb) when perpendicular. In contrast, Bob makes
projective measurements onto a two-particle entangled state, where again the orientation
of the apparatus is defined by the angle,
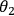 . Bobís outcomes are defined as +1, when
detectors 1 & 2 (red light bulbs) or 3 & 4 (green light bulbs) are firing, or -1 when
detectors 1 & 3 or 2 & 4 are firing. b) When Alice and Bob measure with the same
measurement settings, i.e.
. Bobís outcomes are defined as +1, when
detectors 1 & 2 (red light bulbs) or 3 & 4 (green light bulbs) are firing, or -1 when
detectors 1 & 3 or 2 & 4 are firing. b) When Alice and Bob measure with the same
measurement settings, i.e.
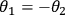 , they observe perfect correlations, which appear in
four possible configurations, given by +1. However, when they measure in a different
basis, i.e.
, they observe perfect correlations, which appear in
four possible configurations, given by +1. However, when they measure in a different
basis, i.e.
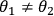 , they will also observe four possible anti-correlations c), given by
-1. The correlation measurements with different measurement settings form the basis of a
test of local realism using entangled entanglement.
, they will also observe four possible anti-correlations c), given by
-1. The correlation measurements with different measurement settings form the basis of a
test of local realism using entangled entanglement.
In Figure 1, a schematic for the experiment is shown in which three photons are prepared in an entangled state
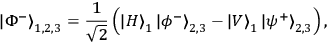
|
1 |
where the subscripts
label different photons, the kets
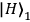 and
and
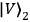 represent states of horizontal and vertical
polarization, respectively, of photon 1 and
represent states of horizontal and vertical
polarization, respectively, of photon 1 and
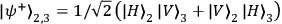 and
and
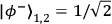
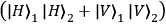 represent two (out of four possible)
so-called Bell-states (maximally entangled states) of photons 2 and 3. Since the entangled state of photons 2 and 3 is entangled with the polarization state of photon 1, the state in Eq. (1) can be referred to as entangled entanglement. Photon 1 is moving
freely in one direction to Alice, while the photons 2 and 3 are moving into the opposite
direction to Bob. Aliceís photon 1 is now subjected to a polarization measurement along
the axis
represent two (out of four possible)
so-called Bell-states (maximally entangled states) of photons 2 and 3. Since the entangled state of photons 2 and 3 is entangled with the polarization state of photon 1, the state in Eq. (1) can be referred to as entangled entanglement. Photon 1 is moving
freely in one direction to Alice, while the photons 2 and 3 are moving into the opposite
direction to Bob. Aliceís photon 1 is now subjected to a polarization measurement along
the axis
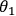 . For simplicity, the settings are restricted to the linear polarization
measurement, i.e.,
. For simplicity, the settings are restricted to the linear polarization
measurement, i.e.,
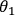 lies within the x-y plane of the Poincaré sphere. If the
polarization is found to be parallel to the axis
lies within the x-y plane of the Poincaré sphere. If the
polarization is found to be parallel to the axis
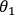 (outcome +1), the photon will be
projected onto the state
(outcome +1), the photon will be
projected onto the state
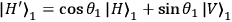 ,
or when to be found perpendicular (outcome -1), it will be
projected onto the state
,
or when to be found perpendicular (outcome -1), it will be
projected onto the state
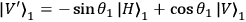 .
Photons 2 and 3 at Bobís side are subjected to a specific
joint measurement that can also only result in two different outcomes. In relation to the experiment, photons 2 and 3 are labelled as B and D, respectively, due to being emitted into the spatial mode B and D (Figure 2). Bob's measurement
setting is denoted by the angle
.
Photons 2 and 3 at Bobís side are subjected to a specific
joint measurement that can also only result in two different outcomes. In relation to the experiment, photons 2 and 3 are labelled as B and D, respectively, due to being emitted into the spatial mode B and D (Figure 2). Bob's measurement
setting is denoted by the angle
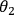 . The measurement will project the two photons onto
either the state
. The measurement will project the two photons onto
either the state
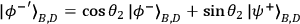 (outcome +1) or
(outcome +1) or
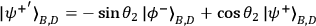 (outcome -1).
The outcome +1 will be identified by
joint registration of photons 2 & 3 at the pairs of detectors, (1 and 2) or (3 and 4),
while the outcome -1 will be identified by firing of pairs of detectors (1 and 3) or (2
and 4). When Alice and Bob choose the orientations
(outcome -1).
The outcome +1 will be identified by
joint registration of photons 2 & 3 at the pairs of detectors, (1 and 2) or (3 and 4),
while the outcome -1 will be identified by firing of pairs of detectors (1 and 3) or (2
and 4). When Alice and Bob choose the orientations
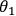 and
and
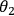 of their measurement
apparatuses the initial state transforms to
of their measurement
apparatuses the initial state transforms to
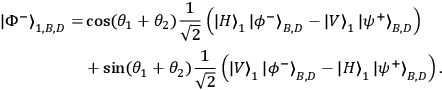
|
2 |
The quantum state in Eq. (1) has the remarkable property that it is the same for any choice of
local settings
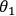 and
and
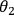 such that
such that
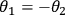 , i.e., it is invariant under this set of locally
unitary transformations. This entails perfect correlations: if polarization along
, i.e., it is invariant under this set of locally
unitary transformations. This entails perfect correlations: if polarization along
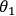 is
found to be +1 (-1) for photon 1, then with certainty the result of the measurement for
setting
is
found to be +1 (-1) for photon 1, then with certainty the result of the measurement for
setting
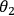 will be found to be +1 (-1) for photons 2 and 3, and vice versa. Because of
the perfect correlations, the result of measuring any entangled state
will be found to be +1 (-1) for photons 2 and 3, and vice versa. Because of
the perfect correlations, the result of measuring any entangled state
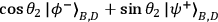 or
or
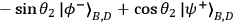 can be predicted with certainty by previously choosing to measure the polarization of photon 1 along the
axis
can be predicted with certainty by previously choosing to measure the polarization of photon 1 along the
axis
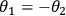 . By locality (in EPR's words):
. By locality (in EPR's words):
Since at the time of measurement the two systems no longer interact, no real change can take place in the second system in consequence of anything that may be done to the first system,
the measurement performed on photon 1 (photons 2 and 3) can cause no real change in photons 2 and 3 (photon 1). Thus, by the premise about reality (in EPR's words):
If, without in any way disturbing a system, we can predict with certainty (i.e. with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical reality,
the entangled states of photons 2 and 3 are elements of reality
for any
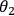 (and similarly for photon 1 and its polarization along
(and similarly for photon 1 and its polarization along
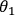 ). Remarkably, the
individual properties of either photon 2 or 3 are not well-defined, as individual
detection events at detectors 1, 2, 3, and 4 are random and cannot be predicted by
previously choosing to measure a property of photon 1. Therefore, the EPR elements of
reality for entangled states of photons 2 and 3 may exist even without existence of these
elements for their individual properties.
). Remarkably, the
individual properties of either photon 2 or 3 are not well-defined, as individual
detection events at detectors 1, 2, 3, and 4 are random and cannot be predicted by
previously choosing to measure a property of photon 1. Therefore, the EPR elements of
reality for entangled states of photons 2 and 3 may exist even without existence of these
elements for their individual properties.
In the following, I will demonstrate that the conjunction of EPR's propositions, which lead to the establishment of entangled states as elements of reality, is in conflict with the quantum-mechanical prediction. This incompatibility will be shown by deriving CHSH Bell inequality [4] for correlations between individual properties of photon 1 and joint properties of photons 2 and 3 from EPR premises and experimental demonstration of their violation by quantum mechanical predictions.
While any Bell state can be converted into any other Bell state by only single-qubit
rotations on one of its constituents Mattle et.al. 1996, the argument is constructed by using a
specific subset of two of the Bell states,
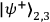 and
and
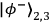 ,
since they are coherently mixed
through the polarization rotation introduced by a half-wave plate (HWP), which makes such an experiment feasible. Using only this HWP,
projective measurements onto maximally entangled states of the form
,
since they are coherently mixed
through the polarization rotation introduced by a half-wave plate (HWP), which makes such an experiment feasible. Using only this HWP,
projective measurements onto maximally entangled states of the form
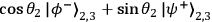 at Bobís side
can be controlled. For consistency throughout this paper, the angle
at Bobís side
can be controlled. For consistency throughout this paper, the angle
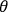 has been
adopted to mean the rotation of a polarization in real space. Thus the same
polarization rotation on the sphere is
has been
adopted to mean the rotation of a polarization in real space. Thus the same
polarization rotation on the sphere is
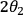 and that rotation is induced by an
HWP
which is itself rotated by only
and that rotation is induced by an
HWP
which is itself rotated by only
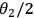 .
.
The experimental setup is explicitly explained in Kwiat et.al. 1995:
The three-photon state is created
using a pulsed ultraviolet laser (pulse duration 200 fs, repetition rate 76
MHz), which makes two passes through a type-II phase-matched
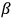 -barium borate
(BBO) nonlinear crystal Mattle et.al. 1996, in such a way that it emits highly
polarization-entangled photon pairs into the modes A & B and C & D (Figure 2).
-barium borate
(BBO) nonlinear crystal Mattle et.al. 1996, in such a way that it emits highly
polarization-entangled photon pairs into the modes A & B and C & D (Figure 2).
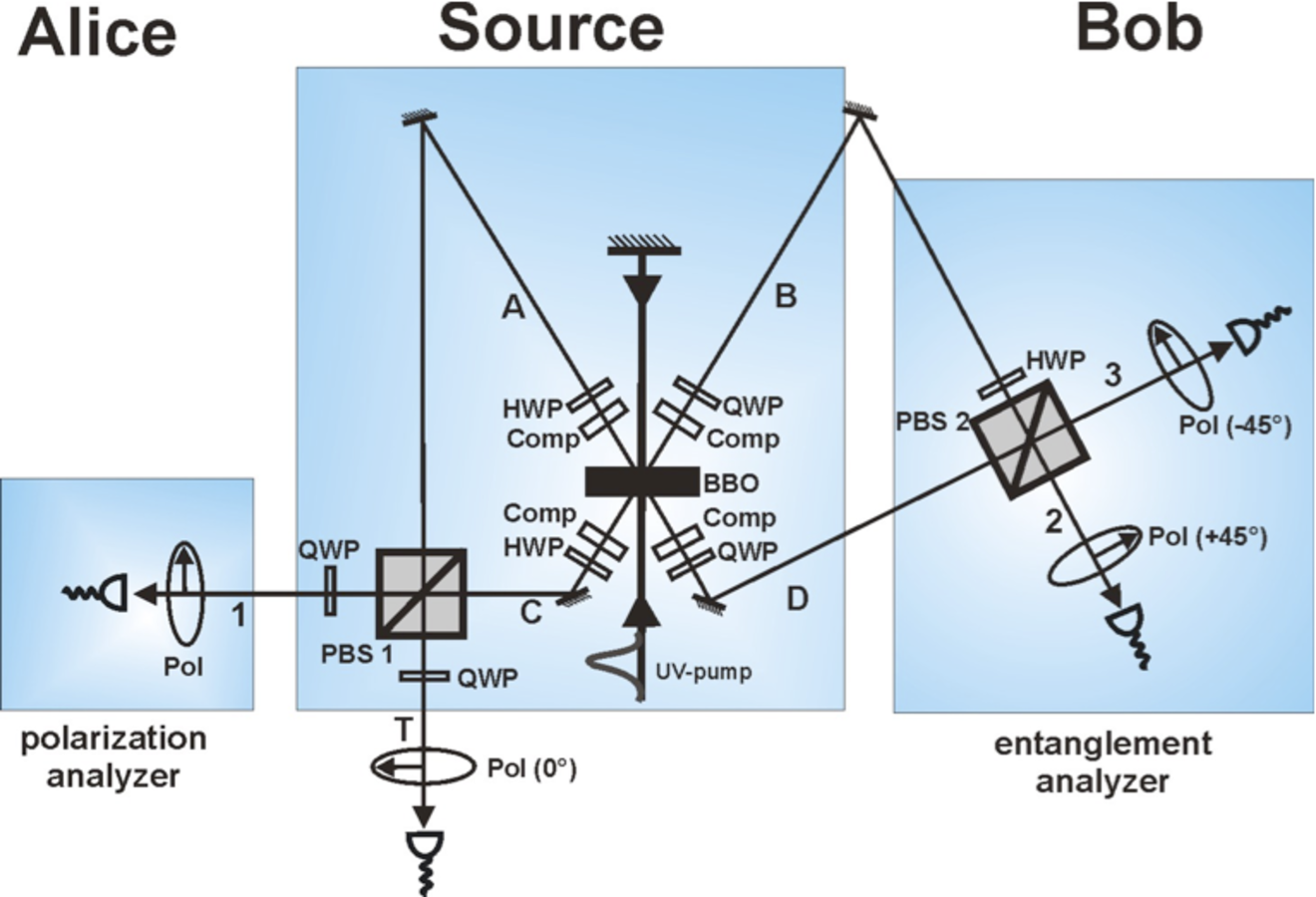
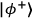 , into both the forward pair of modes A & B and backward pair of modes C & D. After superimposing the modes A & C
at the polarizing beamsplitter PBS1, passing each mode through a quarter-wave plate
(QWP), and projecting the trigger qubit T onto the state
, into both the forward pair of modes A & B and backward pair of modes C & D. After superimposing the modes A & C
at the polarizing beamsplitter PBS1, passing each mode through a quarter-wave plate
(QWP), and projecting the trigger qubit T onto the state
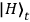 generates the entangled entangled state
generates the entangled entangled state
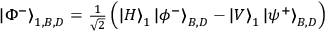 .
The photon in mode 1 belongs to Alice, who uses a linear polarizer for
her single-particle polarization measurements, determined by the angle,
.
The photon in mode 1 belongs to Alice, who uses a linear polarizer for
her single-particle polarization measurements, determined by the angle,
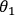 , of her
polarizer. The photons in mode B and D belong to Bob, who uses a modified Bell state
analyzer to make projections onto a coherent superposition of
, of her
polarizer. The photons in mode B and D belong to Bob, who uses a modified Bell state
analyzer to make projections onto a coherent superposition of
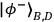 and
and
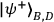 , where the mixing
angle,
, where the mixing
angle,
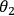 , is determined by the angle,
, is determined by the angle,
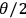 , of the half-wave plate (HWP) in mode B.
, of the half-wave plate (HWP) in mode B.Fig. 2: Setup for the experimental realization. A spontaneous parametric down-conversion source emits polarization-entangled photons in the Bell state,
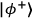 , into both the forward pair of modes A & B and backward pair of modes C & D. After superimposing the modes A & C
at the polarizing beamsplitter PBS1, passing each mode through a quarter-wave plate
(QWP), and projecting the trigger qubit T onto the state
, into both the forward pair of modes A & B and backward pair of modes C & D. After superimposing the modes A & C
at the polarizing beamsplitter PBS1, passing each mode through a quarter-wave plate
(QWP), and projecting the trigger qubit T onto the state
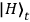 generates the entangled entangled state
generates the entangled entangled state
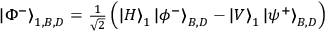 .
The photon in mode 1 belongs to Alice, who uses a linear polarizer for
her single-particle polarization measurements, determined by the angle,
.
The photon in mode 1 belongs to Alice, who uses a linear polarizer for
her single-particle polarization measurements, determined by the angle,
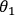 , of her
polarizer. The photons in mode B and D belong to Bob, who uses a modified Bell state
analyzer to make projections onto a coherent superposition of
, of her
polarizer. The photons in mode B and D belong to Bob, who uses a modified Bell state
analyzer to make projections onto a coherent superposition of
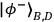 and
and
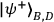 , where the mixing
angle,
, where the mixing
angle,
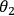 , is determined by the angle,
, is determined by the angle,
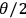 , of the half-wave plate (HWP) in mode B.
, of the half-wave plate (HWP) in mode B.
Transverse and longitudinal walk-off effects are compensated using an HWP and an
extra BBO crystal in each of modes A through D. By additionally rotating the
polarization of one photon in each pair with additional HWPs and tilting the
compensation crystals, any of the four Bell states can be produced in the
forward and backward direction. The source is aligned to produce the Bell state,
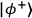 , on each pass of the pump. Photons are detected using fibre-coupled
single-photon counting modules and spectrally and spatially filtered using 3nm
bandwidth filters and single-mode optical fibres. While classically correlated states cannot be correlated at the same time in complementary bases, the quality of entanglement is confirmed by the measured visibilities of each generated photon pair, which exceeded 95% in the H/V basis and 94% in the complementary
, on each pass of the pump. Photons are detected using fibre-coupled
single-photon counting modules and spectrally and spatially filtered using 3nm
bandwidth filters and single-mode optical fibres. While classically correlated states cannot be correlated at the same time in complementary bases, the quality of entanglement is confirmed by the measured visibilities of each generated photon pair, which exceeded 95% in the H/V basis and 94% in the complementary
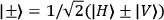 basis.
basis.
Bell pairs contain only two-particle entanglement. To entangle them further, one
photon from each pair needs to be superimposed: those in modes A and C, on a
polarizing beamsplitter (PBS1). Provided those photons overlap at the beamsplitter
and emerge from different output ports, a four-photon GHZ state is generated Mattle et.al. 1996
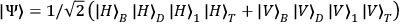 .
The PBS is an optical device that transmits horizontally-polarized photons and reflects
vertically-polarized photons. The PBS implements a two-qubit parity check: if two
photons enter the PBS from the two different input ports, then they must have the
same polarization in the H/V basis in order to pass to the two different output
ports. Then, rotations incurred in quarter-wave plates
(QWP) and the subsequent projection of the trigger photon in mode T onto
.
The PBS is an optical device that transmits horizontally-polarized photons and reflects
vertically-polarized photons. The PBS implements a two-qubit parity check: if two
photons enter the PBS from the two different input ports, then they must have the
same polarization in the H/V basis in order to pass to the two different output
ports. Then, rotations incurred in quarter-wave plates
(QWP) and the subsequent projection of the trigger photon in mode T onto
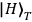 reduces
the four-particle GHZ state to the desired three-photon entangled state
reduces
the four-particle GHZ state to the desired three-photon entangled state
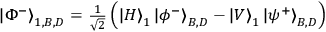 .
.
The polarization of single photons can easily be measured by using linear
polarizers. As is common in Bell experiments, the angle,
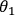 , defines the state on
which the linear polarizers projects. In this work, for Bobís measurement, a
Bell-state analyzer based on a PBS Mattle et.al. 1996 is used. By performing a check that the parity of the photons is even, the PBS acts as a
, defines the state on
which the linear polarizers projects. In this work, for Bobís measurement, a
Bell-state analyzer based on a PBS Mattle et.al. 1996 is used. By performing a check that the parity of the photons is even, the PBS acts as a
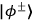 -subspace filter. The two Bell states in this subspace,
-subspace filter. The two Bell states in this subspace,
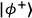 and
and
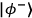 , have opposite correlations in the
, have opposite correlations in the
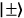 basis and can
easily be distinguished using a pair of linear polarizers. By orienting those linear
polarizers so that one is along the
basis and can
easily be distinguished using a pair of linear polarizers. By orienting those linear
polarizers so that one is along the
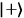 direction and the other along the
direction and the other along the
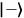 direction, a
projective measurement onto
direction, a
projective measurement onto
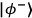 is completed. Since an HWP in mode
is completed. Since an HWP in mode
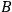 can interconvert
can interconvert
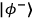 and
and
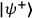 in a controllable way, Alice can choose her projective measurement before her PBS is set to an angle
in a controllable way, Alice can choose her projective measurement before her PBS is set to an angle
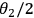 . This is directly analogous to the
projections onto the polarization state.
. This is directly analogous to the
projections onto the polarization state.
Correlation measurements were carried out by rotating Aliceís polarizer angle,
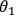 , in
, in
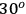 steps while Bob's HWP was kept fixed at
steps while Bob's HWP was kept fixed at
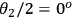 or
or
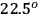 . Four-fold
coincidence counts at each setting were measured for 1800 seconds. These data are
shown in Figure 3.
. Four-fold
coincidence counts at each setting were measured for 1800 seconds. These data are
shown in Figure 3.
 .
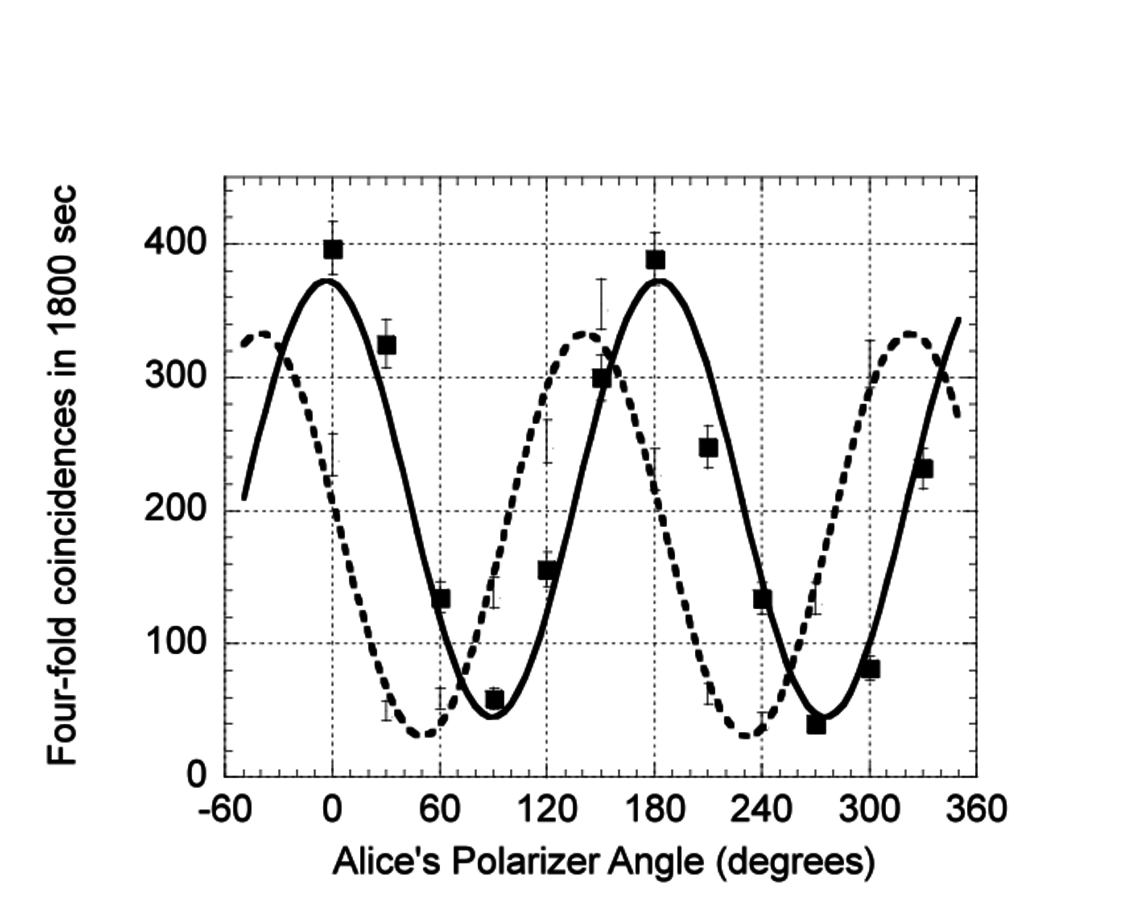
The total number of four-fold coincidence counts measured in 1800
seconds as a function of the angle of Alice's polarizer is shown as solid squares. Fitting
the curve to a sinusoid (solid line) yields a visibility of (
.
The total number of four-fold coincidence counts measured in 1800
seconds as a function of the angle of Alice's polarizer is shown as solid squares. Fitting
the curve to a sinusoid (solid line) yields a visibility of (
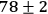 )%. Bob then changed his measurement setting to project onto the state
)%. Bob then changed his measurement setting to project onto the state
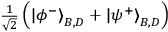 ,
and the procedure was repeated. The data
for these settings are shown as open circles. The sinusoidal fit (dotted line) yields a
visibility of (
,
and the procedure was repeated. The data
for these settings are shown as open circles. The sinusoidal fit (dotted line) yields a
visibility of (
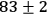 )%.
)%.Fig. 3: Measured coincidence fringes between Alice and Bob for the entangled entangled state. Bobís
half-wave plate was initially set to 0∞, so that he made fixed projective measurements
onto the state
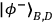 .
The total number of four-fold coincidence counts measured in 1800
seconds as a function of the angle of Alice's polarizer is shown as solid squares. Fitting
the curve to a sinusoid (solid line) yields a visibility of (
.
The total number of four-fold coincidence counts measured in 1800
seconds as a function of the angle of Alice's polarizer is shown as solid squares. Fitting
the curve to a sinusoid (solid line) yields a visibility of (
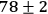 )%. Bob then changed his measurement setting to project onto the state
)%. Bob then changed his measurement setting to project onto the state
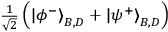 ,
and the procedure was repeated. The data
for these settings are shown as open circles. The sinusoidal fit (dotted line) yields a
visibility of (
,
and the procedure was repeated. The data
for these settings are shown as open circles. The sinusoidal fit (dotted line) yields a
visibility of (
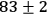 )%.
)%.
The count rates follow the expected relation
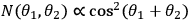 in analogy with the
expected rates from the standard two-particle Bell experiment. The experimentally
obtained data have visibilities of (
in analogy with the
expected rates from the standard two-particle Bell experiment. The experimentally
obtained data have visibilities of (
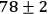 )% in the H/V-basis and (
)% in the H/V-basis and (
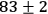 )% in the
)% in the
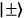 basis. Both of these visibilities surpass the crucial limit of
basis. Both of these visibilities surpass the crucial limit of
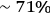 which, in the
presence of white noise, is the threshold for demonstrating a violation of the
CHSH-Bell inequality. Thus, for the proper choices of measurement settings it is
expected that the entangled entangled state should be able to demonstrate a conflict
with local realism using Aliceís polarization state and Bobís maximally-entangled
state.
which, in the
presence of white noise, is the threshold for demonstrating a violation of the
CHSH-Bell inequality. Thus, for the proper choices of measurement settings it is
expected that the entangled entangled state should be able to demonstrate a conflict
with local realism using Aliceís polarization state and Bobís maximally-entangled
state.
For the state,
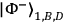 , the expectation value for the
correlations between a polarization
measurement at Bob and a maximally-entangled state measurement at Alice is
, the expectation value for the
correlations between a polarization
measurement at Bob and a maximally-entangled state measurement at Alice is
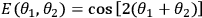 .
The correlation can be expressed in terms of experimentally-measurable counting rates
using the relation
.
The correlation can be expressed in terms of experimentally-measurable counting rates
using the relation
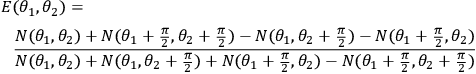
|
3 |
where
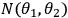 is the number of coincidence detection events between Alice and Bob with
respect to their set of analyzer angles
is the number of coincidence detection events between Alice and Bob with
respect to their set of analyzer angles
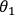 and
and
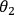 . These correlations can be combined to
give the CHSH-Bell parameter,
. These correlations can be combined to
give the CHSH-Bell parameter,
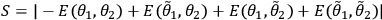 ,
where
,
where
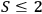 for all local realistic theories. For the settings
for all local realistic theories. For the settings
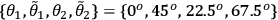 ,
the correlations calculated from quantum mechanics for our
state yields
,
the correlations calculated from quantum mechanics for our
state yields
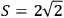 . This value violates the CHSH Bell inequality and is therefore
incompatible with the assumptions of local realism Fry and Thompson 1976.
. This value violates the CHSH Bell inequality and is therefore
incompatible with the assumptions of local realism Fry and Thompson 1976.
In the experiment, four-fold coincidence counts at each measurement setting were
accumulated for 1800 seconds. Each four-fold coincidence signalled 1) the
successful creation of two pairs, 2) the successful entangling operation at PBS1,
3) the reduction of the state to the three photon state onto the requisite state,
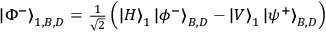 .
.
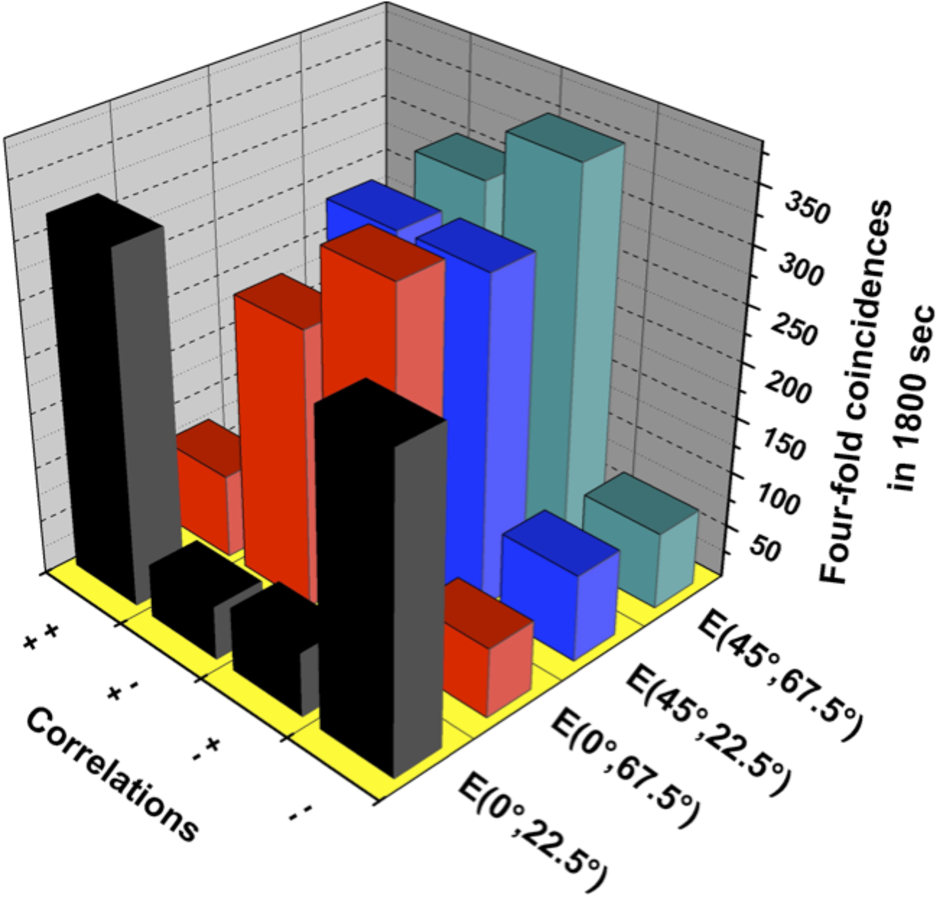
As is shown in Eq. 3, each correlation is a function of four such data points. The counting rates are shown in Figure 4 for the 16 required measurement settings.
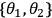 , the axis labels ++, +–, –+, – – refer to the actual settings of
, the axis labels ++, +–, –+, – – refer to the actual settings of
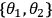 ,
,
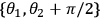 ,
,
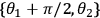 , and
, and
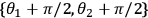 respectively. These data can be
combined to give the Bell parameter
respectively. These data can be
combined to give the Bell parameter
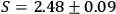 .
.Fig. 4: Experimental results obtained by measuring correlations
for violating a CHSH Bell inequality. The Bell inequality is comprised of 4 correlations,
in this case between the polarization state measured by Alice and the entangled states
measured by Bob. Each of these correlations in turn can be extracted from 4 coincidence
counting rates. The requisite coincidence measurements for the 16 different measurement
settings are shown. Each measurement was performed for 1800 seconds. For measurement
settings,
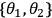 , the axis labels ++, +–, –+, – – refer to the actual settings of
, the axis labels ++, +–, –+, – – refer to the actual settings of
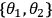 ,
,
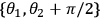 ,
,
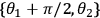 , and
, and
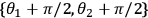 respectively. These data can be
combined to give the Bell parameter
respectively. These data can be
combined to give the Bell parameter
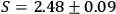 .
.
These counting rates allow us to calculate the four correlations
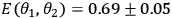 ,
,
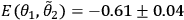 ,
,
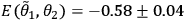 and
and
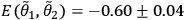 .
Furthermore, those correlations give the experimental Bell parameter,
.
Furthermore, those correlations give the experimental Bell parameter,
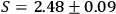 .
This Bell parameter violates the CHSH inequality by
.
This Bell parameter violates the CHSH inequality by
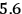 standard deviations.
standard deviations.
3 Conclusion
This year, the Bell inequality turned 47. Since their inception, Bellís inequalities have been the subject of immense theoretical and experimental interest. Initially, this effort was focused on purely foundational issues, but more recently, this work has grown into the burgeoning field of quantum information. Even with all of this attention to this topic, Bell tests have been considered only using single particle properties. The experimental work discussed here is the first Bell test where this restrictive constraint has been lifted.
This result also shows that the naive realistic view of “particles” being physical entities that can be entangled is too simplistic and narrow as no single particle properties are entangled in the present experiment. Therefore from an information-related point of view it only makes sense to speak about measurement events (detector “clicks”) whose statistical correlations may violate limitations imposed by local realism and thus be entangled.
References
Aspect, A., J. Dalibard, J. D. (1982). Experimental test of Bell's inequalities using time-varying analyzers. Phys. Rev. Lett. 49: 1804-1807
Bell, J. (1964). On the Einstein-Podolsky-Rosen paradox. Physics 1: 195-200
Bohr, N. (1935). Can quantum-mechanical description of physical reality be considered complete?. Phys. Rev. 48: 696-702
Clauser, J. F., M. A. Horne, M.A. H., Shimony M. A. (1969). Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23: 880-884
Einstein, A., B. Podolsky, B. P. (1935). Can quantum-mechanical description of physical reality be considered complete?. Phys. Rev. 47: 777-780
Freedman, S.J., J.S. Clauser (1972). Experimental test of local hidden-variable theories. Phys. Rev. Lett. 28: 938-941
Fry, E. S., R. C. Thompson (1976). Experimental test of local hidden-variable theories. Phys. Rev. Lett. 37: 465-468
Greenberger, D., M. Horne, M. H. (1989). Going Beyond Bell's Theorem. In: Bell's Theorem, Quantum Theory, and Conceptions of the Universe Ed. by M. Kafatos. 69-72
Hasegawa, Y., R. Loidl, R. L., Badurek R., B. R. (2004). Violation of a Bell-like inequality in single-neutron interferometry. Nature 425: 45-48
Krenn, G., A. Zeilinger (1996). Entangled Entanglement. Phys. Rev. A54: 1793-1797
Kwiat, P.G., Klaus Mattle, K. M., Weinfurter Klaus, W. K., Harald Weinfurter (1995). New high-intensity source of polarization-entangled photon pairs. Phys.Rev.Lett. 75: 4337-4342
Mattle, K., H. Weinfurter, H. W., Kwiat H. (1996). Dense coding in experimental quantum communication. Phys. Rev. Lett. 76: 4656-4659
Ou, Z. Y., L. Mandel (1988). Violation of Bell's inequality and classical probability in a two-photon correlation experiment. Phys. Rev. Lett. 61: 50-53
Pan, J.-W., D. Bouwmeester, D. B., Daniell D., D. D. (2000). Experimental test of quantum nonlocality in three-photon Greenberger-Horne-Zeilinger entanglement. Nature 403: 515-519
Rowe, M. A., D. Kielpinski, D. K., Meyer D., M. D., V. Meyer, V. M. (2001). Experimental violation of a Bell's inequality with sufficient detection. Nature 409: 791-794
Schrödinger, Erwin (1935). Die gegenwärtige Situation in der Quantenmechanik. Die Naturwissenschaften 23: 807-812
Shih, Y. H., C. O. Alley (1988). New type of Einstein-Podolsky-Rosen-Bohm experiment using pairs of light quanta produced by optical parametric down conversion. Phys. Rev. Lett. 61: 2921-2924
Tapster, P. R., J. G. Rarity, J.G. R. (1994). Violation of Bell's inequality over 4 km of optical fiber. Phys. Rev. Lett. 73: 1923-1926
Tittel, W., J. Brendel, J. B., Zbinden J. (1998). Violation of Bell inequalities by photons more than 10 km apart. Phys. Rev. Lett. 81: 3563-3566
Vaziri, A., G. Weihs, G. W. (2002). Experimental two-photon three-dimensional quantum entanglement. Phys. Rev. Lett. 89: 240401-240405
Walther, P., K. Resch, K. R., Brukner K. (2006). Experimental entangled entanglement. Phys. Rev. Lett 97: 020501-020505
Zeilinger, A., M. Horne, M. H. (1992). Higher-Order Quantum Entanglement. In: Squeezed States and Quantum Uncertainty Ed. by D. Han, Y.S. Kim, Y. K.. NASA Conference Publication 3135.
