The Conserved Quantity Theory of Causation and Entangled States

Abstract. I will argue that processes in Quantum Field Theory can be understood in terms of a new version of the conserved quantity theory of causation. The idea is that causation is the transfer of energy-momentum from cause to effect. This has implications for further topics in the interpretation of quantum physics. I will adopt a proposal due to David Wallace for describing quantum entities as localized in regions of space and show how this gains plausibility by setting it into the context of causation. With this background, I will argue that pre-measurement entangled states are not a structure of two or more related entities, but one spatially extended entity.

1 Introduction

In this paper, I will investigate two widely discussed topics of philosophy of physics: causation and entanglement. Regarding the first one, I will argue that there is causation in physics and regarding the second, I will argue that entanglement should not be understood as a (causal) relation.

The discussion about causation in physics was opened by Bertrand Russell 1912-1913, but only proliferated from the 1980s on with works amongst others by Philip Kitcher and Wesley Salmon (1989) on explanation and causation and by Nancy Cartwright 1989 on capacities. The conserved quantity theory of causation (CQT) identifies causation as the physical process of the exchange of a conserved quantity between physical entities. The latest version of this theory was formulated by Phil Dowe in 2000, and has mostly been neglected, mainly because it is hardly compatible with modern physics. However, in Sections 2, 3 and 4, I will try to revive the core idea of CQT by showing how it can successfully be applied to Quantum Field Theory (QFT).

Entangled states and EPR-correlations were introduced by Einstein, Podolsky and Rosen to demonstrate the incompleteness of quantum mechanics. With the work of John Bell and follow-up experiments, they became an enigma. I see two main problems which are involved here. (1) The problem of localization: How can events be correlated over space-like distances? (2) The measurement problem: How can a superposition of states evolve into distinct states with definite properties? In this paper, I am only concerned with the first problem, which is related to causation. When trying to explain entangled states, the question arises whether there is a causal relation between two entangled objects. To evaluate this, we need criteria that tell us what a causal relation is. This motivates Sections 2, 3 and 4. Should it turn out that there is no causal relation involved in entangled states, we need an alternative explanation of the EPR-correlations. This motivates Sections 5 and 6.

The conclusion will be that, before a measurement happened, entanglement between systems can neither be understood as causal relation nor in other structuralistic terms. The alternative picture, that I will draw, is one in which quantum mechanical entities are not (always) localized in a small region of spacetime, but can be extended over a larger region. Accordingly, an entangled state is not a structure formed by two or more entities and a relation, but one extended entity.

2 What Is Causation and How Do We Find It?

Causation is one of the topics in philosophy where there is huge disagreement among scholars. Is there causation or not? If yes, what kind of relation is it? These are just the two most fundamental questions surrounding the subject. Furthermore, there is a vast field of proposals for what causation could be. The range of possibilities reaches from necessary connections over contingent regularities over to manipulation by humans. The ample nature of the concept of causation makes it difficult to even find a starting point for one's investigation.

Phil Dowe introduced a sensible distinction into this discussion, which in my eyes should stand at the beginning of every new proposal for what causation could be; it is the distinction between conceptual and empirical analyses of causation. Conceptual analysis is the task “to elucidate our normal concept of causation,” whereas empirical analysis tries “to discover what causation is in the objective world“ Dowe 2000, 1. The conceptual analysis sets out to clarify the use of the word “causation” in ordinary language. In principle, every competent speaker of a certain language can perform conceptual analysis, without looking into the world. The aim is to explain the concept of causation by expressing it through other concepts, that are better understood, and to spell out the logical consequences of this explication. Empirical analysis, on the other hand, intends to find a process in the world, which can be identified as being a causal process. This is an empirical investigation and thus cannot be accomplished without taking notice of our best sciences; for they are the place to look at, if we want to know how the world is like.

Dowe acknowledges that the distinction is not clear-cut. The ambiguity is made obvious by the asymmetry between both methods of analysis. While conceptual analysis proceeds without taking empirical knowledge into account (though it may have consequences for our way of looking at the world), the empirical analysis is dependent on preliminary conceptual analysis. It is impossible to make plausible that any physical process is a causal relation without having at least a vague understanding of what we mean when we use this concept. If empirical analysis is not backed up by conceptual analysis it could be claimed of anything that it is causation. However, Dowe holds this to be unproblematic. In his eyes, conceptual knowledge about causation is already encoded into science, since scientists are competent speakers of their working language. Hence, we only have to look into science for suitable processes and the conceptual work is already done by the scientists.

Dowe's seemingly `careless' stance is criticized by Thomas Bontly 2006. He argues that it is unclear how and to which extent the tacit knowledge of scientists about causation is comprised in their scientific theories. Therefore, it is ambiguous whether and how the empirical analysis can be carried out. At least some explicit criteria for what causation is are required before we look into science and see whether there is something that meets them.

It is difficult, if not impossible, to find necessary and sufficient criteria for what causation is. Like Bontly 2006, 192f., I will present plausible criteria, due to several different authors, that a concept of causation has to suffice. This list is not intended to give all and only necessary conditions. Nevertheless, the criteria should be sufficient to identify a physical process as causal and make the choice at least reasonable.

1Causation is an (intrinsic) relation between distinct entities Menzies 1996, 98.

I hold this criterion to be necessary for causation. The conditions under which entities count as distinct need to be specified later. “Intrinsic” means that the causal relation is independent of everything except the entities that are causally related. I have put “intrinsic” in brackets, because Humeans about causation do not agree on this. Leaving it out does not much harm in the context of this paper. Furthermore, it is important to note that the relation needs to be specified, in order to accomplish the aim of explaining what causation is. The relation could be for instance spatial connection (one object hitting the other) or a physical force.

2One can manipulate the effect by manipulating the cause Bontly 2006, 193.

This criterion is central for physical practice. Whenever something is changed on the (alleged) cause, something should happen to the (alleged) effect. In the extreme, the effect should disappear when the cause is removed. I take manipulability to be the second necessary criterion for causation. A slightly different criterion, that has nevertheless the same consequences, is expressed by H. D. Mellor 1988, 230: “If an effect is an end, its causes are means to it.”

3The cause typically increases the chance of the effect Menzies 1996, 100.

This leaves the possibility open for chance-lowering causation. However, in general we should observe the effect more often when the cause is present, compared to when it is not. This seems to be neither a necessary nor a sufficient criterion for causation. Nevertheless, if one finds a chance raising relation, this is a good indicator that one has found a causal relation.

4Causation is a stable relation between cause and effect.

This is a rather vague statement. The interpretation depends on the actual stance one takes towards causation. If one wants to defend a non-Humean theory of causation then “stable” means “necessary.” If on the other hand one wants do defend a Humean theory, then “stable” might mean “regularly.” Additionally, stability is supposed to catch the central meaning of two further criteria by Mellor 1988, 230, namely “causes and effects are evidence for each other,” and “causes explain their effects.”

Some authors hold a fifth criterion to be essential for causation,¹ that I will neglect in the following:

1Causes precede their effects in time Bontly 2006, 193.

In my eyes, this is neither necessary nor sufficient for causation, but something we should leave to physics to decide. If we can identify causation by using the other four criteria then it might be the case that this relation has a fixed order in time. However, it might as well turn out that the order is changed under certain circumstances. The latter, I think, has no influence on whether we found a causal relation or not.

The line of argument now will be first to present Dowe's empirical theory of causation and discuss how it fares in the light of modern physics. The deficiencies of Dowe's theory that show up motivate an updated version of it. Then, in chapter 4, I will show that the first four criteria mentioned above can be applied to QFT and present the updated empirical theory of causation.

3 Phil Dowe's Conserved Quantity Theory

The conserved quantity theory (CQT) is an empirical analysis of causation. Hence, it identifies a process in the world that should fit the criteria mentioned in the last chapter. The idea is that causation is the exchange of a conserved quantity between the cause and the effect. For example in the (classical) Compton effect one photon hits an electron, whereby the momenta of both are changed. If the interaction is free from other influences, then the change of the momenta could only happen by the exchange of momentum between the photon and the electron.

The CQT, in slightly different versions, has already some decades of history; it was first introduced by Jerrold Aronson 1971 then reconsidered by David Fair 1979 and discussed between Phil Fair 1979 and Wesley Fair 1979. To make a long story short, I will only discuss the latest and most elaborate version of the CQT due to Phil Dowe. It can be put succinctly into three statements:

CQ1. A causal process is a worldline of an object that possesses a conserved quantity.

CQ2. A causal interaction is an intersection of world lines that involves exchange of a conserved quantity Dowe 2000, 90.

CQ3. There is a causal connection (or thread) between a fact q(a) and a fact q'(b) if and only if there is a set of causal processes and interactions between q(a) and q'(b) such that:

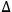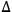1any change of object from a to b and any change of conserved quantity from q to q' occur by way of a causal interaction involving the following changes: q(a), q(b), 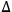q'(a), and 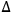q'(b); and

2for any exchange in (1) involving more than one conserved quantity, the changes in quantities are governed by a single law of nature Dowe 2000, 171f.

A few explanations are needed here. A worldline is the trajectory of an object in Minkowski spacetime. An object is a member of the set of things, which make up the fundamental ontology of physics. Only objects exist; processes and worldlines are solely means to represent the time evolution of objects and their causal interactions. A conserved quantity is every property that is subject to a conservation law in physics. An intersection is the meeting of worldlines in a Minkowski spacetime. An exchange is the corresponding change of the value of one conserved quantity of at least two objects. Please note that Dowe uses the notion of exchange deliberately to avoid any connotation of transfer of a conserved quantity; where transfer means that exactly the same quantum of a conserved quantity, that is lost by the cause, is acquired by the effect. For us to be using the term transfer instead of exchange, following Dowe, it would be necessary to be able to define identity conditions for amounts of physical quantities, which is not possible Dowe 2000, 90f.

The first definition, CQ1, is supposed to capture cases where one object is at the same time the cause and the effect. An example is an object that is moving uniformly in space, where the only cause of the motion is the object's own inertial mass. CQ2 is the definition for simple causal processes, in which cause and effect are directly linked by hitting each other. In cases where cause and effect are not directly linked, because there is another process in between, the definition of a causal connection comes into play. Two examples will help to make things clearer, one example is simple and the other one more complicated:

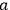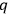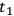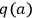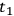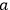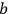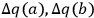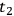1The Compton effect is the fundamental interaction between light and matter. In a (classical) description, the cause is electron with energy at time ( at ). The causal interaction is the intersection of the worldlines of electron and photon , which changes the energies of both ( ). The effect at time is photon 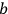with a smaller energy than at time 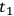( 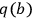at ).

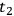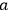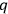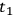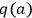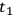2A photon hits an atom and is absorbed. As a result, the atom decays to a different atom with different charge. The cause is photon with energy at time ( at ). The first causal interaction is the intersection of photon 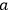with atom 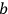, in which 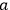exchanges energy with 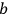( 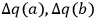). The second interaction is the decay of atom 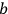to atom 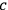, in which energy 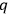and charge 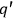are exchanged ( 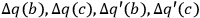). Following the definition of a causal connection, the effect is atom 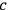with charge 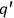at time 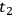( 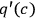at 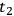) Dowe 2000, 172 f..

It has been criticized that the CQT is circular, because what a conserved quantity is can only be defined by invoking causation: “A conserved quantity is one that remains constant through time in a closed system, but what is a closed system but a system that does not engage in any causal interaction?” Hitchcock 1995, 315f. Dowe responds by arguing that for instance energy can be defined in a different way: “energy is conserved [...] on the assumption that there is no net flow into or out of the system” Dowe 2000, 95. However, it is unclear whether “net flow” is something other than a causal process Schaffer 2001, 810. Nevertheless, this critique is ineffective, since the CQT is not an analytic definition of the concept of causation. If it were, of course, conceptual circularity would be severe. However, the CQT aims at an empirical, rather than conceptual, analysis of causation. It aims to identify processes in the world that can be understood as causal, and this can be done without caring about conceptual circularity.

Unfortunately, there are more problems with Dowe's CQT, especially when trying to fit it to quantum physics. First of all, Dowe's definition of a causal process seems to be obsolete. His only example for a causal process is a case where the inertial mass of an object is the cause for its uniform motion. However, it is clear from the theory of special relativity that uniform motion in one inertial frame is rest in another one and that both frames are on a par with each other, since there is no absolute space or other sort of preferred reference frame. Additionally, CQ1 is in conflict with our intuition that causation involves at least two distinct entities, which can play the roles of cause and effect. Consequently, I do not see any reason why uniform motion should be in need of a causal explanation. Second, the notion of worldlines is highly problematic in quantum physics. The Heisenberg uncertainty principle tells us that an object cannot have a sharp position and a sharp momentum at the same time. Additionally, in general states in quantum physics are not eigenstates but superpositions, so most objects do not have a sharp value of any property. Therefore, it is impossible to define the worldline of an object. This, in turn, makes Dowe's notion of “exchange” opaque, for exchange cannot be defined as the intersection of worldlines. Furthermore, there is no worked out ontology for QFT, so we are ignorant of what the objects of this theory are. This makes it questionable that Dowe's CQT, which is defined in terms of objects, can be applied to QFT.²

If the CQT has no answer to these problems, it is certainly a poor theory of causation in physics. In the next chapter, I will take a look into QFT to see whether these problems can be met. It will turn out that according to the four criteria for causation from Section 2 there is causation in QFT. Furthermore, I will introduce a new CQT, adjusted to QFT, that retains from Dowe's theory only the core idea that causation is the exchange of energy.

4 Causal Processes in Quantum Field Theory

Adrian Heathcote 1989 already argued that QFT can be interpreted as describing causal interactions between fundamental objects. This seems immediately plausible; after all, while quantum mechanics can only describe the dynamics of one particle alone or in a potential and interactions only in very simplified models, QFT is the physical theory that broadens quantum mechanics to include interactions. Hence, “all causal influences are the result of forces between objects, all such forces are interactions in the sense of QFT“ Heathcote 1989, 101f. However, neither did Heathcote bring his theory of causation into precise form, as Dowe did, nor did he show explicitly how the mathematical formalism of the QFT supports his claims. This is what I will do in the following.

I solely rely on the Lagrangian formulation of QFT (LQFT). This probably needs a few words of justification, since most philosophers of physics nowadays discuss the algebraic approach (AQFT). At this place, I can only give a short sketch of the discussion. Roughly, there are two arguments of AQFT proponents against LQFT. (1) LQFT is in a way mathematically ill defined that is in conflict with its claim to describe the fundamental physical world. (2) The rigorous mathematical formalism of AQFT is eo ipso superior to study the foundations of QFT. The first sort of argument usually criticizes that the renormalization methods in LQFT are a mathematically ill defined and ad hoc way to squeeze empirical predictions out of LQFT Heathcote 1989, 101f. On the contrary, David Heathcote 1989, 101f argues that today it is well understood how divergencies arise due to the failure of LQFT on high energies respectively small distances. Therefore, renormalization methods, that cut off small distances, are “on a sound theoretical footing” Wallace 2011, 118. Nonetheless, it has to be admitted that this failure of LQFT could mean that we need a new physical theory for very small distances. Another less problematic justification for the use of renormalization methods is that spacetime might fundamentally be grained or quantized and therefore it makes no sense to try to investigate very small regions of spacetime Peskin and Schroeder 1995, 266–268, 798.

As for the second point in favour of AQFT, I do not hold it to be conclusive. The claim that mathematical rigor is important for a scientific theory has to be supported by an argument. How could this argument look like? Presumably, it is tacitly presupposed that nature follows exact mathematical laws Halvorson 2007. However, I do not see any other way to support this claim than by physical research. This points to a different perspective on the conflict. From the (meta-)perspective of a scientific realist certainly LQFT is the superior theory. Scientific realism is supported by the no miracles argument, that allows inferring from the success of a theory to the reality of the world that is described by it Psillos 1999. Since LQFT is without doubt the most successful physical theory we have, what else could philosophers of physics be realist about if not LQFT? In contrast, AQFT “makes no (non-falsified) empirical predictions whatsoever [and] there is, at present, just no reason to expect that program to succeed” Wallace 2011, 120. To end this excursus, I want to add that investigation in AQFT, nevertheless, is a worthwhile program and it will be interesting to see whether an ontological framework for AQFT, should any be found, contradicts the picture drawn by LQFT.

After these preliminaries, I will now go into LQFT to find out how far the mathematics can be interpreted in line with the CQT. My treatment of LQFT will be rather informal and, for the sake of brevity, I will only mention the mathematical expressions to which I explicitly refer in order to establish my claims about causation. Usually the calculation of a certain process in LQFT starts with the stipulation of a Lagrangian density. For a typical scattering process, like 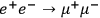in quantum electrodynamics, the Lagrangian density is given by (following Greiner and Reinhardt 1996 and Peskin and Schroeder 1995)

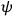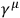The electrons/positrons for the initial and the muons/anti-muons for the final state are specified by the field ( ), the Dirac-matrices , and by the mass 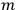. They have Energy 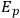, momentum 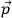, polarized spin 1/2 and electric charge 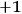(resp. 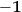). The electromagnetic force is described by the field 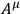(resp. the field-strength tensor 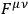) and 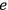, its coupling constant. 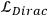is the typical Lagrangian for a massive spin-1/2 particle³, 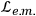is the Lagrangian for the electromagnetic force and 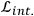specifies the coupling of the other two. From 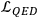coupled equations of motion for the fields 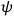, 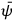and 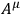can be derived.

What needs to be calculated to obtain the probability of a scattering process, that is the probability of an evolution of a certain initial state to a certain final state, is essentially the overlap of in and out states:

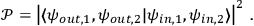
In and out states are usually wavepackets of the form

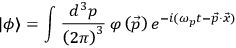
in the time limit 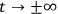:⁴

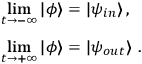
The wavepackets have a momentum that is peaked in momentum space around the definite value 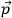. They are related via the time limit evolution by a unitary operator

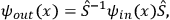
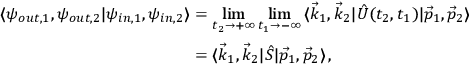
where 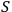is the so called 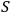-matrix. In and out states are taken to represent particles which are free, long before and after the interaction. Strictly speaking this is an idealization, since in nature the interaction can never be completely turned off. However, for in and out states it becomes negligibly small.

In the canonical quantization formulation of QFT, the fields become operator fields (sometimes this is called “second-quantization”). For the matter field this means

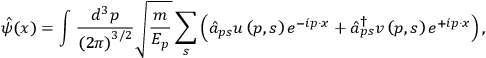
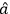where for each particle in the initial state there must be a lowering operator , and for each particle in the final state there must be a raising operator 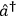. 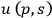and 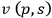are plane wave base functions with momentum 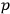and spin 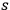. Note that, unlike in quantum mechanics, in QFT momentum and energy are classical quantities (c-numbers, in Dirac's terminology). Letting raising and lowering operators act on the vacuum state we create particle states:

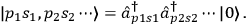
Furthermore, the 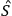operator has to be expanded into a perturbation series, where the interaction part of the Lagrangian is written in terms of the free asymptotic operator fields and their dynamics. In the leading order of the series, the probability amplitude 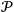is then given by the invariant 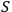-matrix element 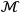. Essential for obtaining the probability is the evaluation of vacuum expectation values for time ordered operator fields (i.e. n-point Green's functions):

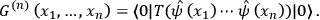
For 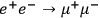this can in practice more or less just be read off from the proper Feynman diagram and turns out to be (invoking various symmetry considerations):

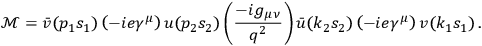
Here 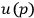and 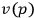are spinors that describe the matter-fields, the terms 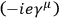describe the vertices (i.e. the coupling of the matter-fields) and the middle term describes virtual photons with momentum 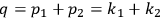. From 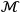the differential scattering cross-section can be calculated in a straightforward manner:

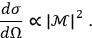
The differential cross-section is basically a distribution of energy in space and is measured as the final result of experiments—this is where theory is compared to empirical data. Of course, energy-momentum is conserved over the whole process.

The same result, i.e., the element of the -matrix and the differential cross-section, can be found via the equivalent way of the path integral method. Again, what needs to be calculated is the overlapping of an initial with a final state, both of which are eigenstates of the operator field

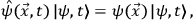
and are related by a unitary operator:

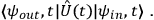
Only this time, the result is obtained not by calculating vacuum to vacuum transitions with the help of raising and lowering operators, but by evaluating path integrals, 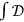, over `classical' (i.e. not operator) fields of the form (following Greiner and Reinhardt 1996, ch. 9.2)

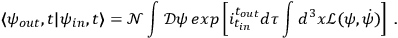
The matrix element 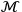is then given by

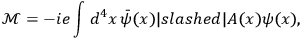
which leads to the exact same matrix element and differential cross section as the canonical quantization above.⁵

The reality of the in and out going particles is uncontroversial–at least for scientific realists. In contrast, the reality of the virtual or, how I rather like to call them, intermediate particles, from which the factor 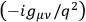in 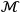stems, is far from clear. Since I will rely on intermediate particles when arguing for causation, I need to provide arguments for their reality.

In canonical as well as in path integral QFT, the Feynman propagator for photons takes on the form:

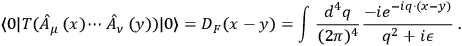
In a naive interpretation, this might be the probability amplitude for a point-like photon to travel from point 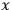to point 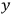in spacetime. However, the well known arguments against a point-particle interpretation undermine this naivety. Particles, whatever they may be, do not have classical trajectories and it is questionable in how far they exist locally in spacetime at all. Additionally, there are specific arguments against the realistic interpretation of intermediate particles. They are prima facie suspicious, since they are not measurable `directly'; unlike the initial and final states, they do not appear in bubble chambers or other measurement devices. It is questionable whether they are more than a mathematical part of a perturbation series. However, “if something cannot be `directly' observed that doesn't mean we cannot have indirect evidence of its existence” Weingard 1982, 235. After all, intermediate particles are an indispensible part of a successful theory, and therefore we have good evidence for their reality. Additionally, photons and other particles that play the roles of intermediate particles do exist as free states and can be `directly' observed. To be precise, however, it has to be admitted that intermediate particles have more polarization degrees of freedom than their free counterparts. Therefore, not all kinds of intermediate particles exist as free states. Furthermore, intermediate particles do not have to be on mass shell, that is, fulfil the relativistic relation 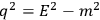. This does not mean that intermediate particles violate energy conservation. Any fluctuation in energy has to happen on very small timescales, i.e., in accordance with the energy-time uncertainty relation.

The main argument against intermediate particles comes from superpositions.⁶ In general, the Feynman propagator cannot be calculated directly, but only in a perturbation series. The final amplitude then is the superposition of the parts of the series and, so the argument goes, therefore there are no discrete particles represented by the parts of the perturbation series. However, this is shared by all kinds of particles in QFT and cannot count as an argument against intermediate particles in particular. Instead, this is just another argument against the literal interpretation of single Feynman diagrams as showing real processes and trajectories. Superpositions do not show that intermediate particles in general do not exist, but that it is only the whole process that has a consistent realistic interpretations and not individual parts of it Falkenburg 2007, 237.

Johanna Seibt 2002, 58 challenged philosophers to decide, which QFT should be interpreted: AQFT, LQFT (canonical quantization) or LQFT (path integral formulation). With regard to AQFT, I have already stated my position. Concerning the latter two, I do not see how and why only one formulation could be singled out, because they are fully equivalent. Instead, I see only one possibility, that is, to find an interpretation compatible with both formulations (e.g. not relying on ladder operators). In the following, I highlight three characteristics of the canonical and the path integral formulation, on which I will rely later:

• Initial and final states: Initial and final states are defined as not interacting at times long before and after the scattering. In this regard, these states are distinct from one another. They carry a well defined quantity of energy-momentum and have properties that are characteristic for a certain kind of entity (spin, mass, charge).

• Local conservation laws: All conservations laws in QFT are local. Thus, either the amount of a certain property in an arbitrary small region of spacetime is constant, or there is a current going through the surface of that region.

• Intermediate states: Intermediate states carry the complete energy-mo-

mentum of the initial respectively final states. Even though they cannot unambiguously be interpreted as a localized spatial process mediating the energy-momentum they exist in between the initial and final states.

With this background, let me now formulate a new version of the CQT and then discuss how it differs from Dowe's version and why it should still be called causation. The definition is not supposed to be self-contained, but has to be read in light of the foregoing explanations.

• C causes E iff: C is an initial state and energy-momentum is transferred from C by an intermediate state to a final state E.

In comparison to Dowe's CQT, I want to emphasize first of all that initial and final states are not the equivalent to Dowe's objects. For Dowe, talking about objects involves having an ontology, also Dowe's objects have well defined trajectories in Minkowski diagrams. In contrast to this, initial and final states are just what is defined by physics; they are underdetermined concerning ontology. For now, it is not clear whether they are more like classical particles or more like fields or something else and surely they do not have well defined trajectories. This is unproblematic when trying to identify a causal relation. The four criteria in Section 2 are applicable without any information about what kinds of objects we are dealing with. Their formulation is independent of whether cause and effect are point-particles or fields or something else. Therefore, it is possible to identify causal relations in QFT without knowing what kinds of entities initial and final states are.

Second, take the process 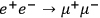. While Dowe distinguishes between the electron and the positron, or the muon and anti-muon, respectively, and would take either only one as the cause, the effect, or both as separate causes, or effects (see examples one and two in Section 3), I take the electron and positron together as the cause, and the muon and anti-muon together as the effect. The deficiency of Dowe's account can be seen by way of an example. 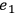Two electrons and 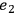with momenta 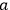and 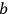scatter and the momenta change to 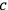and 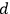. 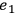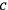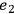Whether after the scattering has and 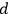or vice versa cannot be answered in QFT and both possibilities have to be taken into account in the calculation of the scattering amplitude Greiner and Reinhardt 2009, ch. 3.3. Therefore, it is not possible to divide the final state in two separate effects and I do not see how and why it should be otherwise for the cause.

Third, I make use of local conservation laws in so far as the causal processes in QFT are continuous processes, though not localized in spacetime. Global conservation of energy-momentum would allow a quantity of energy to cease to exist at one point in space and at the same time come to existence at another distant point in space. Local conservation laws rule out such events, because regions of spacetime can be made arbitrary small and either the amount of a conserved quantity is constant in that region or there is a current into, or out of, that region. This justifies the view that causation is the transfer of energy-momentum and not just the exchange. I do not, to be clear, defend the position that causal processes in QFT are localized in the sense that everything is moving on thin lines, pictured in Feynman diagrams.

Fourth, it is enough to understand causation only as the transfer of energy-momentum and not of every conserved quantity there is. Energy-momentum is always relevant, it is transferred in every process in QFT and it is the property that is controlled and measured in experiments (most of the time this will happen together with position measurements, in order to measure the distribution of energy in space).

Finally, it is time to ask whether the relation of energy-momentum transfer satisfies the criteria of Section 2, whether it actually is a causal relation. As for the first criterion, the relation is intrinsic, since scattering events, if they are sufficiently isolated in experiments, do not depend on anything else that is going on in the universe. The relata, initial and final states, are distinct by definition, long before and after the scattering, and energy-momentum transfer shows what the relation between the relata exactly is. Moreover, it is almost trivially true that the effect can be manipulated by manipulating the cause; a change in the momentum of the initial state will always change the momentum of the final state. Even though, in quantum physics initial states only produce a final state with a certain probability (the matrix element 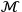), to take the previous example, the probability to observe a muon anti-muon pair in a collider is certainly higher when electrons and positrons collide as compared to when they do not. These probabilities are objective in a sense that they can be reproduced in experiments. Therefore, it is reasonable to think of the relations that are described by QFT as stable relations.

I conclude that QFT can be understood as describing causal processes, i.e., as the transfer of energy-momentum. In the next two sections, I will put causation to work when applying it to the problems of localization and entanglement.

5 The Problem of Localization

States in QFT are usually defined as wavepackets. In experiments, they are focused and localized fairly well by the use of collimators and interactions happen on timescales that are small enough for them to keep their shape. However, no matter how well the collimators work, the wavepacket will not have the form of a delta function, exactly peaked in spacetime and momentum space, but it will have the form of a Gaussian. Since every Gaussian is non-zero everywhere in space, there is a non-vanishing probability for a positive result when measuring an initial or final state everywhere in space. Does it follow that, whatever states are, every state exists everywhere in the universe, whether we measure it or not? This is (one formulation) of the problem of localization in quantum physics.

A promising, but flawed, way to avoid this seemingly counterintuitive conclusion are so called Newton-Wigner states Newton and Wigner 1949. These states are exactly localized in coordinate space and have a position operator 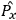that gives an expectation value of one for a state 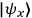localized at spacetime point 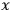, i.e., 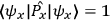, and an expectation value equal to zero for any point 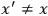, i.e., 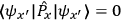. David Malament 1996 has proven that Newton-Wigner states are inconsistent with special relativity. In the interest of brevity, I will not repeat the proof here but only point out where exactly the contradiction arises. One consequence of special relativity is microcausality. 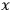An event at some point in spacetime is independent of any event at point 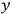that is space-like separated from 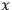. In quantum physics, this is expressed by an equal time commutator relation. If two observables commute

then the outcomes of measurements of these observables are independent of one another.⁷ This condition cannot be satisfied by Newton-Wigner states. If the probability for a measurement outcome at 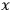is one, then the probability in a space-like separated point 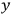must be zero. 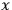In other words, the statistics of both measurements are not independent of one another.⁸ This dependence could only be established by a signal with superluminal velocity between and 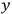. This is impossible according to special relativity. Therefore the conclusion of Malament's theorem is that Newton-Wigner states and special relativity are only compatible if the probability for a positive measurement outcome for any observable is zero everywhere in space. This is clearly unacceptable and therefore Newton-Wigner states have to be abandoned.

In general, there is no position operator in QFT. However, since “[a]ll quantum field theories [ ......] model localization by making observables dependent on position in spacetime” Halvorson and Clifton 2002, 18, any observable 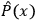, defined at spacetime point 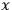, is sufficient to refer to an entity localized at 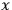. Here again the problem of localization arises, since this attitude, taken by itself, means that all states in QFT exist at every spacetime point in the universe.

Several authors point to experiments in particle physics, which seemingly show the measurement of small particles, and come to the conclusion that “there remains a particle `grin'” Redhead 1982, 89 “which cannot be dismissed” French and Krause 2006, 136.<sup>9</sup> Electrons and photons show up as dots on scintillation screens or photographic plates, 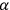-particles leave tracks in bubble chambers, and so on. It is argued that if the fundamental entities are always measured as localized events, then clearly these entities have to be small particles; this seems to be self-evident and in no need of further explanation. However, on a closer look, this argument turns out to be fallacious. What we are looking for in an ontology are entities that are the cause of observable phenomena. Even if we infer from the observable phenomena that there is something that causes them, we cannot automatically infer that the cause in some ways resembles the phenomena. If we want to find out more about the causes, it is the theory that we have to consult. Halvorson and Clifton 2002, 22 put this argument into a different form when they assert: “In particular, we do not observe particles; rather, there are `observation events' .” Even though the things that we observe (tracks in bubble chambers etc.) are localized, we do not observe particles but only the effect of a physical interaction between a fundamental entity and the measurement apparatus. Not our observations tell us how the fundamental entities are like, but theory. It might look as though we observe localized particles, however, “[t]hese experiences are illusory!” Halvorson and Clifton 2002, 20.¹⁰

In this impasse, David Falkenburg 2007 introduced a new conception of how quantum mechanical states could be described as localized in space, which he calls effective localization. It, and the accompanying principle of effective localization (ELP), can be defined as follows Wallace 2001, 10:

1Effective localisation (qualitative form): A state 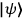is effectively localised in a spatial region 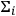iff for any function 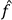of field operators 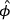, , 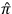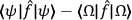is negligibly small when 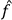is evaluated for field operators outside 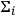, compared to its values when evaluated for field operators within .

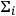2The effective localisation principle (ELP) (qualitative form): A subspace 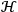of the QFT Hilbert space 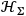obeys the ELP on scale L iff for any spatial region 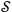large compared with L, a superposition of states effectively localised in 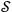is effectivey localised in effectively the same region.

Essentially this means that a state 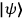, in order to be localized in spatial region 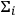, must have expectation values for a set of operators 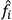considerably bigger than the vacuum state 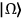has for .

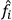Even though I agree with Wallace, I see two problems. (1) Defining localization in such a way seems to be an ad hoc move, only motivated by rescuing some form of localization. Any setting of L is just arbitrary. (2) Wallace is aware that effective localization is only an approximation, but an ontology that tells only what things there are approximately is unacceptable. Is there any way to justify effective localization independently and improve the approximation? I think there is – when effective localization is put into the context of causation.

To see this, two points have to be made explicit. In discussions about scientific realism it is often stressed that we can only reasonably be realistic about unobservable entities that cause observable phenomena.¹¹ In addition to that, if QFT is understood as describing causal relations between states, the states themselves should be regarded just as what is causally relevant for the process. In this light, the question then is: What is causally relevant for the processes in QFT? Is it a part of the state 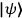in spatial regions 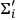where no experiment, possible today, could find any difference between 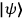and the vacuum state 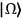? I do not think so. From the viewpoint of scientific realism and causation we have no reason to believe in something that has no observable effects for our experiments. Therefore, effective localization is neither ad hoc nor an approximation, but a description of entities in whose existence we can have justified belief.

6 Entanglement

In this section, I will explore what follows for the interpretation of entangled states, if causation in QFT and effective localization are taken for granted.

There are two problems involved in entanglement: (1) How can space-like separated events be correlated without having a common cause? (2) How can a superposition evolve into definite states upon measurement? The latter is of course the measurement problem—which I will not treat here. The former question, however, can be investigated to some extent without invoking the measurement problem.

John Bell has shown that EPR-correlations cannot be explained by a common cause, which determines the probabilities of the measurement outcomes of the entangled state. The question as to how space-like correlations are possible, then, can be transferred to whether there is a causal connection or relation of some other sort between entangled particles. A paradigm example for entanglement is the singlet state of two electrons:

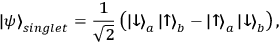
where 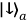means that electron 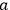has spin state down etc.

Tim Psillos 2006 argues that EPR-correlations can be understood as a causal relation between entangled objects. Of course, he is aware that “[c]orrelation does not imply causation” Maudlin 2002, 127. Nonetheless, he believes it to be justified to analyse EPR-correlations in terms of a counterfactual theory of causation: “The local physical events A and B are causally implicated with one another if B would not have occurred had A not (and vice versa)” Maudlin 2002, 128. Where the notion of “is causally implicated with” is considerably weaker than the usual notion of “is caused by.” Here is Maudlin 2002, 128 again: “We do not suppose that it follows from the fact that A is causally implicated with B that A caused B or B caused A.” But this makes the relation of causal implication too weak to be still called causation. In fact, I see no difference between causal implication and correlation. No doubt, if we know that B would not have occurred had A not and vice versa, then A and B are correlated. However, if A is correlated with B means “A 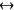B,” then we can infer from “A is correlated with B” that if B does not occur so does not A, in other words, A had not occurred if B had not (and vice versa).¹² If I understand Maudlin correctly, then causal implication means nothing more than a counterfactual, but this makes causal implication and correlation equivalent, since either one follows from the other.

To be fair, this is not the complete position of Maudlin. He is also realistic about natural laws and argues that laws tell us which counterfactuals and causal implications are true:

Since it is facts about the laws that help us identify the cause [ ...] and since laws are obviously deeply implicated in the evaluation of counterfactuals, I suggest that we stop trying to analyze causation directly in terms of counterfactuals and consider anew how laws play a role in determining causes. Maudlin 2007, 148

Setting aside the problem whether physical theories give a set of laws, Maudlin is silent about which law it is that shows that EPR-correlations are more than mere correlations. As far as I can see, the physical description of EPR-experiments only tells us that if we measure the spin on electr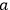on  , then a subsequent measurement of electron 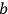 's spin will yield the opposite result, and vice versa—this is correlation and nothing more.

Maybe there are other reasons for holding entanglement and EPR-correlation to be a causal relation. Let us apply the criteria for causation from Section 2. It is clearly true that EPR-correlations are stable relations and if A is correlated with B, then A trivially increases the chance of B. Thus, two criteria out of four are already fulfilled. What about the other two? Can we manipulate one entangled electron by manipulating the other? Before the measurement, from a theoretical as well as an experimental standpoint, this is impossible. First of all, the entangled state cannot be split up into two separate parts that are then manipulated separately. In addition to that, every experimental manipulation on the entangled property (e.g., spin) would destroy the entanglement and therefore cannot count as manipulation. However, maybe measurement is nothing else than a manipulation; after all, the alignment of the magnetic field when measuring the spin of electron a alters the outcome of a measurement of electron b's spin. Fair enough, but now we entered the realm of the measurement problem and it is, to say the least, unclear what happens in a measurement. While decoherence theories may describe measurements as something that alters the measured states, the GRW-flash theory probably does not. In short, before the measurement happens we can certainly not manipulate entangled states and what happens due to the measurement is completely unclear.

The same result is obtained when considering the first criterion, causation as intrinsic relation between distinct entities. Intrinsicness is probably fulfilled, but before the measurement there is no reason to believe in distinct entities. Entangled states, unlike product states, are governed by only one Hamiltonian and therefore there are not two or more things that evolve independently. Also, no physical relation between two parts of an entangled state is measured or appears in the theoretical description. This critique generalizes from causal relations to any relation. It is unclear how entangled states could be described as a relation between distinct entities without any account of how the entities can be defined or what the relation physically is. Again this reasoning is only tenable as long as measurements are neglected.

Is there any alternative to the description of entanglement as a relation? Taking the previous chapter into account, I think there is. If an entangled state (e.g., ) does not consist of two distinct entities, then it can be either cause or effect, but not describe cause and effect at the same time. Furthermore, the discussion of localization has shown that there are in general no point particles, but only entities that exist in spatially extended regions. Applied to entangled states, Wallace's effective localization means that one entangled state is just one entity that is extended in space. Of course, this means that there are entities extended over 20 km and more, but since pointlike entities are no option anyway, this is just another new thing that quantum physics tells us about the world.

To explicate this alternative picture to relationalism, an entangled state should be regarded as one relatum of a causal interaction with a measurement device that has as effect two separated states. Before a measurement happens, the entangled state is just one entity; the measurement destroys the entanglement and leaves two or more distinct entities. This is essentially a different picture (cf. Maudlin) than that of a measurement device that acts on one part of an entangled state, which then causes something in the other part of the entangled state. Though again, this point has no sufficient justification until the measurement problem is solved.

To sum up, an entangled state does not consist of two distinct entities that are measured at space-like distances, but only of a single extended entity that most often is detected in one place (which detection supposedly disrupts the entanglement). However, this does not help much to understand EPR-correlations; it just shifts all the burden over to the measurement problem. What I hope to have shown is that the focus of investigation needs to be transferrred, or else the whole problem has to be reformulated. The question is not how one entangled entity can have causal influence on the other one, but what happens at the measurement. Any discussion whether EPR-correlations are compatible with special relativity misses the point, because there is no reason to believe that some sort of causal or other relation is involved in the formation of entangled states. Rather, the measurement problem needs to be solved, no less and no more, to make entanglement and EPR-correlations less puzzling.

Acknowledgment

I want to thank Michael Esfeld, Tilman Sauer and Adrian Wüthrich for organising the conference and letting me present my unfinished thoughts, as well as the audience and an anonymous reviewer for helpful comments.

References

Footnotes