Abstract. Quantum gravity is supposed to be the most fundamental theory, including a quantum theory of the metrical field (spacetime). However, it is not clear how a quantum theory of gravity could account for classical phenomena, including notably measurement outcomes. But all the evidence that we have for a physical theory is based on measurement outcomes. We consider this problem in the framework of canonical quantum gravity, pointing out a dilemma: all the available accounts that admit classical phenomena presuppose entities with a well-defined spatio-temporal localization (“local beables” in John Bell's terms) as primitive. But there seems to be no possibility to include such primitives in canonical quantum gravity. However, if one does not do so, it is not clear how entities that are supposed to be ontologically prior to spacetime could give rise to entities that then are spatio-temporally localized.
Introduction
The research for a theory of quantum gravity (QG), that is, a theoretical framework that extends quantum (field) theory to a theory of gravity, is one of the most long-lived enterprises in modern physics. The term “gravitational quanta” was used for the first time by Léon Rosenfeld 1930, but today—more than 80 years later—there is still no well established physical theory of quantum gravity.
There currently are two main types of approaches to QG. The first one, dubbed covariant QG, seeks to find a unification of all the fundamental interactions known in nature by enlarging the standard model of particle physics in order to include gravity, considered as a massless spin-2 field whose quanta are called gravitons: (super)string theories are the most notable variant of this type of approach.1 The other type of approach, called canonical QG—the most worked out representative of which is, today, loop quantum gravity (LQG)2—focuses on elaborating a formulation of general relativity (GR) suitable of being quantized using a physically well-defined procedure like, for example, Dirac's (1964) procedure; in this case, it seems more appropriate to talk about spacetime geometry rather than the gravitational field as the entity being quantized. For brevity's sake, the paper will deal only with the latter approach.
Although they are work in progress, both covariant and canonical approaches have so far produced many results of physical relevance,3 showing that at least the leading theories of both types are rather well-developed. Therefore, a philosophical reflection on the foundations of QG is not only a legitimate enterprise, but a necessary step to be taken in order to achieve a better understanding of the conceptual issues involved in the field. Moreover, any theory of quantum gravity has to be empirically adequate, that is, it has to be able to account for the measurement results in quantum physics. In this paper, we shall therefore give an account of canonical QG and consider the challenges in getting from canonical QG to an account of classical phenomena such as measurement outcomes.
1 Canonical Quantum Gravity: A Brief Sketch
The canonical strategy aims to give a quantum description of gravitational phenomena by first formulating the conceptual machinery of GR in a Hamiltonian form and then using the methods of canonical quantization. The “recipe” for canonically quantizing a classical system can be summarized as follows. Given a physical system with
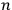 degrees of freedom coordinatized by the configuration variables
degrees of freedom coordinatized by the configuration variables
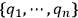 , its Lagrangian
, its Lagrangian
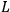 will satisfy Hamilton's action principle
will satisfy Hamilton's action principle
 , where
, where
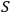 is the usual action defined as:
is the usual action defined as:
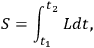
|
1 |
which leads to the Euler-Lagrange equations4:
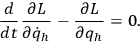
|
2 |
We define the momenta
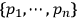 conjugate to the configuration variables as
conjugate to the configuration variables as
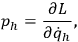
|
3 |
and we generate the Hamiltonian
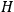 of the system by a Legendre transformation:
of the system by a Legendre transformation:
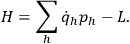
|
4 |
This procedure amounts to switching the system's description from the coordinate system
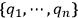 in the
in the
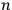 -dimensional configuration space
-dimensional configuration space
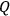 to the coordinate system
to the coordinate system
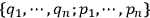 in the
in the
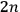 -dimensional phase space
-dimensional phase space
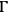 . The dynamics of the system is now encoded in the Hamiltonian equations of motion obtained by applying Hamilton's principle to the action (1) where
. The dynamics of the system is now encoded in the Hamiltonian equations of motion obtained by applying Hamilton's principle to the action (1) where
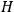 is given by (4):
is given by (4):
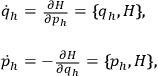
|
5 |
where the binary operation
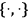 is the classical Poisson bracket. Such a system can be easily quantized by replacing the phase space
is the classical Poisson bracket. Such a system can be easily quantized by replacing the phase space
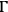 with the Hilbert space of complex functions on
with the Hilbert space of complex functions on
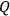 which are square-integrable with respect to Lebesgue measure and by introducing the quantum commutator
which are square-integrable with respect to Lebesgue measure and by introducing the quantum commutator
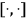 as the quantum mechanical analog of the Poisson bracket. All the classically observable quantities are now self-adjoint operators defined over (a subspace of) the Hilbert space. A function
as the quantum mechanical analog of the Poisson bracket. All the classically observable quantities are now self-adjoint operators defined over (a subspace of) the Hilbert space. A function
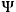 belonging to this space is the wave function corresponding to a given quantum state of the system whose dynamics is encoded in the Schrödinger equation5:
belonging to this space is the wave function corresponding to a given quantum state of the system whose dynamics is encoded in the Schrödinger equation5:
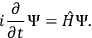
|
6 |
In the case of GR, one would expect that, since the theory has a well-behaved Lagrangian formulation, the above procedure, mutatis mutandis, would be carried out without particular problems. However, as we shall see in a moment, constructing a Hamiltonian formulation of GR is far from trivial and can be carried out only for a particular subset of models of the theory.
In the classical case6, the Hamiltonian description of a system tells us how its dynamical state
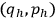 evolves in absolute time. Moreover, the procedure which took us from (1) to (6), has been carried out only in the very simple case in which all the degrees of freedom of the system are physical. It may in fact happen that the solutions of the Euler-Lagrange equations (2) cannot be uniquely determined by specifying a set of initial conditions
evolves in absolute time. Moreover, the procedure which took us from (1) to (6), has been carried out only in the very simple case in which all the degrees of freedom of the system are physical. It may in fact happen that the solutions of the Euler-Lagrange equations (2) cannot be uniquely determined by specifying a set of initial conditions
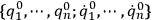 , thus being determined only up to an arbitrary function of time.7 This means that we have the “freedom” to choose this function without altering the physical description of the system. The immediate consequence of this fact is that the transformation (3) turns out to be non-invertible, i.e. there are further relations of the form
, thus being determined only up to an arbitrary function of time.7 This means that we have the “freedom” to choose this function without altering the physical description of the system. The immediate consequence of this fact is that the transformation (3) turns out to be non-invertible, i.e. there are further relations of the form
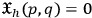 called “constraints” between some of the dynamical variables. In this case, things become more complicated because now there is no more a one-to-one correspondece between Lagrangian and Hamiltonian, and the latter is determined only up to a linear combination of the constraints:
called “constraints” between some of the dynamical variables. In this case, things become more complicated because now there is no more a one-to-one correspondece between Lagrangian and Hamiltonian, and the latter is determined only up to a linear combination of the constraints:
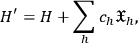
|
7 |
where
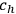 are unknown coefficients and
are unknown coefficients and
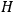 is the “unconstrained” Hamiltonian. Hence, the equations of motion (5) now read
is the “unconstrained” Hamiltonian. Hence, the equations of motion (5) now read
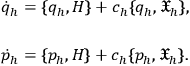
|
8 |
In order to stress the fact that the constraint relations must be handled after the evaluation of the Poisson brackets, it is said that they vanish “weakly” and it is written
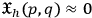 .
.
The constrained Hamiltonian formulation is of paramount importance in the treatment of systems that exhibit gauge invariance. The physical significance of the constraint relations, in fact, is that some degrees of freedom of the system are not physical but just gauge and would be eliminated by solving the constraints (“fixing the gauge”). For this reason, the quantities of most physical relevance for a constrained system - the observables - will be the gauge invariant ones, i.e., those quantities that have weakly vanishing Poisson brackets with the constraints. A similar remark can be made in the case of GR, since general relativistic systems exhibit a feature closely related to gauge invariance, i.e. general covariance8, which simply speaking amounts to the fact that the physical description of a system is independent on the particular coordinatization chosen. Moreover, GR is a background independent theory, and a consequence of this feature is the absence of a primitive notion of time being intended either in a Newtonian or in a Minkowskian sense. Hence, we would expect a Hamiltonian formulation of GR not only to exhibit constraints but also to treat time as a degree of freedom of a gravitational system.9
Just to have a schematic idea of what it means to consider time as a degree of freedom of the system, let us consider the toy example of a classical non-relativistic particle.10 To make things even more simple, let us take the particle to have unit mass and only one spatial degree of freedom
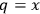 . If a one dimensional potential
. If a one dimensional potential
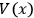 is present, then the Lagrangian of the particle will be
is present, then the Lagrangian of the particle will be
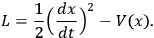
|
9 |
In this extremely simple case, the procedure (1)-(6) is straightforward. But what happens if we “parametrize” Newtonian time, i.e., if we consider
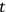 as a new degree of freedom? In this case, once we have chosen a suitable real parameter
as a new degree of freedom? In this case, once we have chosen a suitable real parameter
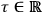 , the new Lagrangian becomes:
, the new Lagrangian becomes:
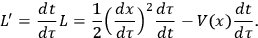
|
10 |
The relation between the two Lagrangians stems from the fact that they must be both compatible with the same action (1), so it must be
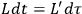 . Now let's use equation (3) to calculate the momenta conjugate to
. Now let's use equation (3) to calculate the momenta conjugate to
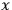 and
and
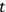 . We find
. We find
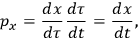
|
11a |
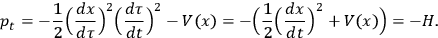
|
11b |
We immediately notice that the “new” momentum conjugate to
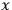 is the same as in the “unparametrized” case, while the time conjugate momentum is nothing but the opposite of the Hamiltonian corresponding to the original Lagrangian
is the same as in the “unparametrized” case, while the time conjugate momentum is nothing but the opposite of the Hamiltonian corresponding to the original Lagrangian
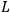 . The “new” Hamiltonian can be quickly calculated from (4) to yield:
. The “new” Hamiltonian can be quickly calculated from (4) to yield:
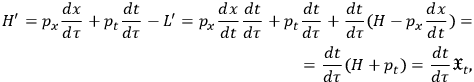
|
12 |
where the Hamiltonian corresponding to the “old” Lagrangian has been introduced through (10) and (4). Equation (12) is slightly more complicated than (7) because it also accounts for the fact that
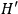 is a parametrized version of
is a parametrized version of
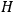 but, nonetheless, the fact that
but, nonetheless, the fact that
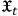 is a constraint arising from (11b) comes out clearly. Obviously, in this case, the equations of motion cannot be calculated directly from (8), but must be evaluated by considering (4) and then using the action principle (1)
is a constraint arising from (11b) comes out clearly. Obviously, in this case, the equations of motion cannot be calculated directly from (8), but must be evaluated by considering (4) and then using the action principle (1)
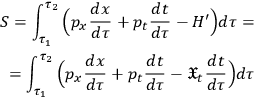
|
13 |
together with the condition
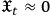 . Up to now, we have somewhat followed steps (1)-(5) of the canonical quantization procedure. To “translate” the system into the quantum regime we just substitute the dynamical variables with operators acting on the Hilbert space of wave functions of the system:
. Up to now, we have somewhat followed steps (1)-(5) of the canonical quantization procedure. To “translate” the system into the quantum regime we just substitute the dynamical variables with operators acting on the Hilbert space of wave functions of the system:
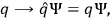
|
14a |
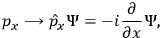
|
14b |
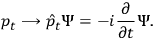
|
14c |
The remarkable point is that, in case of a constrained system, the only allowed wave functions that encode possible descriptions of the system are those which satisfy the quantum version of the constraints, in this case, taking into account definitions (14), we have:
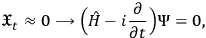
|
15 |
which is, as expected, the usual Schrödinger equation for a single particle. This example may seem rather twisted and artificial but helps us to straightforwardly point out a few important features of the canonical quantization procedure applied to constrained Hamiltonian system. The first is that, while an unconstrained system can be always quite easily parametrized and de-parametrized, i.e., we can always single out and eliminate the “extra” unphysical degrees of freedom, the opposite is not so simple, i.e., given a constrained system, it is in general far from trivial to determine which degrees of freedom are physical and which are not (GR is a clear example of such complexity). The second point is that, for a quantized constrained system, the Hilbert space of possible states of the system does not coincide with the “physical” Hilbert space, i.e., the space of solutions of the dynamical equations of motion (in the previous case, equation (15)). This means that, the more the constraints are complex, the more difficult it will be to sketch how the corresponding physical Hilbert space will look like.11 However—and this is the third point—even simple constraints not always generate a trivial dynamics. A clear example of this is again (15). Bearing in mind these results, we can now take a closer look at the Hamiltonian formulation of GR.
Historically, the first to accomplish this task—thus completing the work by Dirac 1958—were Arnowitt, Deser and Misner Arnowitt et.al. 2004, who elaborated the so called ADM formalism. To cut short, we can say that the Hamiltonian formulation of GR must describe how a suitably chosen parametrized physical entity changes for different values of the parameter. A reasonable move to perform before seeking for such physical entity is to put ourselves in the most simple situation possible, i.e., the case in which our general relativistic system consists of nothing but a pure gravitational field.12 Even in this simplified case, however, there seems to be no natural candidate unless we further restrict ourselves to spacetimes that admit foliations into
 -surfaces
-surfaces
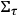 : if the
: if the
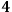 -manifold has in fact a topology of the type
-manifold has in fact a topology of the type
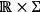 , then we can straightforwardly interpret the Hamiltonian formalism of GR as describing how the
, then we can straightforwardly interpret the Hamiltonian formalism of GR as describing how the
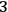 -surfaces of the foliation
-surfaces of the foliation
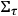 change by varying the parameter
change by varying the parameter
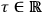 . The most intuitive configuration variables to be adopted in this context are the
. The most intuitive configuration variables to be adopted in this context are the
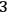 -metrics
-metrics
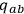 defined on the
defined on the
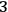 -surfaces and their conjugate momenta
-surfaces and their conjugate momenta
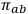 which encode information on how a given surface is embedded in the
which encode information on how a given surface is embedded in the
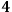 -manifold, i.e., its extrinsic curvature. The ADM formalism follows exactly this line of reasoning but adds a further simplification, i.e., it considers only globally hyperbolic spacetimes, so that the
-manifold, i.e., its extrinsic curvature. The ADM formalism follows exactly this line of reasoning but adds a further simplification, i.e., it considers only globally hyperbolic spacetimes, so that the
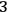 -surfaces of the foliation are space-like (Cauchy surfaces)13 and the parameter
-surfaces of the foliation are space-like (Cauchy surfaces)13 and the parameter
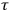 can be chosen as a global time function.14 In short, ADM formalism splits the
can be chosen as a global time function.14 In short, ADM formalism splits the
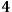 -dimensional spacetime into space and time. In this way we can switch the “foliation view” to a more intuitive picture of a single spatial
-dimensional spacetime into space and time. In this way we can switch the “foliation view” to a more intuitive picture of a single spatial
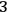 -manifold
-manifold
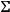 evolving in “time”
evolving in “time”
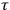 : this is why the ADM formalism is commonly referred to as “geometrodynamics.”
: this is why the ADM formalism is commonly referred to as “geometrodynamics.”
The immediate worry of such a splitting of the
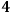 -dimensional GR in a
-dimensional GR in a
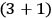 theory is that the original
theory is that the original
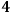 -diffeomorphism invariance (which is preserved in the Lagrangian formulation) would be broken. Fortunately, this is not the case, since the diffeomorphic invariant character of the theory is now captured15 in a set of constraints whose basic meaning is that not all points
-diffeomorphism invariance (which is preserved in the Lagrangian formulation) would be broken. Fortunately, this is not the case, since the diffeomorphic invariant character of the theory is now captured15 in a set of constraints whose basic meaning is that not all points
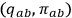 in the phase space represent genuine physical states, i.e., different points related to different but diffeomorphic configurations represent the same physical situation. In general, we speak of a “diffeomorphism constraint,” which encodes the
in the phase space represent genuine physical states, i.e., different points related to different but diffeomorphic configurations represent the same physical situation. In general, we speak of a “diffeomorphism constraint,” which encodes the
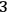 -diffeomorphism invariance of the
-diffeomorphism invariance of the
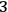 -manifold
-manifold
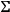 , and a “Hamiltonian constraint,” which accounts for the fact that the formalism does not depend on the specific parametrization adopted, i.e. on the particular choice of the paramenter
, and a “Hamiltonian constraint,” which accounts for the fact that the formalism does not depend on the specific parametrization adopted, i.e. on the particular choice of the paramenter
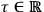 . We can collectively refer to these constraints as
. We can collectively refer to these constraints as
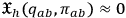 . In the end, then, the full Hamiltonian description for GR will be given by an action principle analog to (13). With all this machinery in place, we can now quantize the theory. We can choose either to solve first the constraints and then to quantize or the other way round: the most common choice is the latter, because it slightly simplifies the calculation, however—at least in principle—both choices lead to the same final results. The immediate consequence of the presence of constraints is that the dynamical evolution of a “gravitational state”
. In the end, then, the full Hamiltonian description for GR will be given by an action principle analog to (13). With all this machinery in place, we can now quantize the theory. We can choose either to solve first the constraints and then to quantize or the other way round: the most common choice is the latter, because it slightly simplifies the calculation, however—at least in principle—both choices lead to the same final results. The immediate consequence of the presence of constraints is that the dynamical evolution of a “gravitational state”
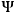 will be generated by a set of equations that resemble (15):
will be generated by a set of equations that resemble (15):
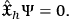
|
16 |
Equations (16)—often collectively referred to as Wheeler-DeWitt equation16— highlight two major (and interrelated) problems in canonical QG, which are inherited from the classical regime. The first one is the problem of observables. If we take a physically relevant quantity as one which has weakly vanishing Poisson bracket with the constraints (in the classical case) or as an operator that “produces” states annihilated by the constraints17 (in the quantum case), then the only observables of both theories will be quantities that do not change in time. This issue is a direct consequence of the so called “problem of time,” i.e. the impossibility to define a classical notion of time neither in GR nor in canonical QG. The Hamiltonian formulation of GR emphasizes this issue by suggesting that any possible notion of time merely refers to a gauge fixing and, hence, is unphysical. An escape route might be to distinguish between quantities compatible only with the diffeomorphism constraints (“observables”) and quantities compatible also with the Hamiltonian constraint (“perennials”), as suggested for example by Kuchar̆ 1993. Another possible solution is to discriminate between quantities associated with measurements (“partial observables”) and quantities whose value or probability distribution can be predicted by the theory (“complete observables”) as suggested by Rovelli 2002. This, of course, partially shifts the problem onto finding a consistent account of measurement in the quantum gravitational context. Tackling these issues is the main task if we want to shed light on a route that leads from the quantum gravitational regime to classical phenomena.
2 The Measurement Problem of Quantum Mechanics
As regards the account of classical phenomena, the very formulation of non-relativistic quantum mechanics poses a problem that is known as the measurement problem. Relativistic quantum mechanics—that is, quantum field theory—faces this problem as well. Quantum gravity being the project of unifying quantum field theory with general relativity theory, it is not to be expected that quantum gravity will solve the measurement problem. Nonetheless, any approach to quantum gravity that is to be empirically adequate has to take a stance on the measurement problem, the question being how to account for measurement outcomes within a quantum theory, including a quantum theory of gravity. Let us therefore go into this problem and consider its consequences for a theory of quantum gravity.
A clear conceptualization of the measurement problem can be found in Maudlin 1995, 7:
1A The wave-function of a system is complete, i.e., the wave-function specifies (directly or indirectly) all of the physical properties of a system.
1B The wave-function always evolves in accord with a linear dynamical equation (e.g. the Schrödinger equation).
1C Measurements of, e.g., the spin of an electron always (or at least usually) have determinate outcomes, i.e., at the end of the measurement the measuring device is either in a state which indicates spin up (and not down) or spin down (and not up).
The problem is that there can be no formulation of a quantum theory that respects all three of these propositions, because their conjunction is inconsistent: if the wave function yields a complete description of the properties of a system and if it always evolves according to a linear dynamical equation, then it cannot evolve in such a way that it represents a quantum system as having a determinate value of a dynamical property—such as a definite position or a definite value of spin–and a measuring device as indicating such a determinate value.
The notion of measurement is immaterial to the formulation of this problem. There is no physical definition of what a measurement is: measurement interactions are not a special type of interactions in addition to the strong, the weak, the electromagnetic, and the gravitational interactions, but are simply ordinary physical interactions; and measuring devices are not natural kinds in addition to electrons, protons, the chemical kinds, biological species, etc. Any macroscopic system capable of amplifying the properties of quantum systems can be used as a measuring device. One can therefore replace proposition 1C above with the following, slightly more complicated proposition that does not refer to measurements, but only to positions of macroscopic systems:
1C* The macroscopic systems with which we are familiar—such as, e.g. tables, trees, cats, people, and the like—always (or at least usually) have determinate positions in space, and these systems are composed of microscopic quantum systems.
Consequently, quantum systems, whatever they are, must at least sometimes have positions that are determinate enough so that they can compose macroscopic systems that have determinate positions. But if the wave function specifies all the properties of quantum systems and if the wave function always evolves in accord with a linear dynamical equation, it is impossible that quantum systems have positions that are determinate enough so that they can compose macroscopic systems that have determinate positions, due to the superposition principle and the entanglement of the states of quantum systems.
3 Two Conservative Solutions of the Measurement Problem
The measurement problem shows that if one retains 1C or 1C*—that is, the proposition that macroscopic systems usually have definite positions in space or spacetime—one has to give up either 1A or 1B. Such solutions can be regarded as conservative in the sense that they retain the ordinary presupposition of macroscopic systems having definite positions in space or spacetime so that measurements have definite outcomes.
If one drops 1A and thus maintains that the wave function does not tell the whole story about what there is in the physical world, the only precisely formulated theory that elaborates on this idea is Bohm's quantum mechanics Maudlin 1995, 7. Bohm's theory starts from the trivial fact that macroscopic systems such as measuring devices cannot have a determinate position unless the microscopic systems that compose them also have a rather determinate position. It then adds the—controversial—claim that these microscopic systems cannot acquire a rather determinate position in space and time unless they always have one. In other words, Bohm's theory introduces a determinate value of position for any physical system as an additional variable that is not specified by the wave function. This variable is hidden in the case of microphysical systems in the sense that it is not possible to find out the exact positions of microphysical systems without changing them. On this basis, the quantum probabilities have the same status as the probabilities in statistical mechanics, namely to yield all the knowledge that we can obtain given our ignorance of the exact initial conditions. In short, the ontology of Bohm's theory consists in particles whose positions are correlated with each other and a global law of motion (sometimes referred to as quantum potential or guiding field or pilot wave), spelling out how the positions of the particles taken together develop in time.18
It may seem that since Bohm's quantum theory works in terms of particles, it is a non-starter when it comes to quantum field theory and quantum gravity. However, the point of Bohm's theory is to provide an ontology of quantum physics by answering the question of what the formalism tells us about the physical world in terms of it referring to positions of something; that answer is justified by arguing that if the fundamental physical objects, whatever they are, were not characterized by determinate positions, macroscopic objects could not have determinate positions either. The question is whether that latter claim is correct. That claim is not tied to conceiving the fundamental physical objects as enduring particles. Indeed, since Bell 1987, ch. 19, there are proposals for a Bohmian quantum field theory around,19 and there also is a sketch of a Bohmian theory of quantum gravity Goldstein and Teufel 2001. The basic idea behind this sketch is to recover a notion of time from (16) as a hidden variable. The starting point20 is to consider only the diffeomorphism constraint as encoding the gauge freedom of the theory and to take the Hamiltonian constraint as some sort of stationary Schrödinger-like equation which involves a “universal” wave function. Under this framework, we can say that each spacetime point carries three “distinct pieces of physical information” or, less metaphorically speaking, at each point on a
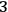 -surface
-surface
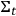 a coordinate system can be found where the
a coordinate system can be found where the
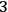 -metric
-metric
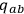 is represented by a
is represented by a
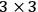 matrix in diagonal form with these three pieces of physical information being just the elements on the diagonal. Two of these pieces of information account for the gravitational field (according to the view that gravity is a massless spin-
matrix in diagonal form with these three pieces of physical information being just the elements on the diagonal. Two of these pieces of information account for the gravitational field (according to the view that gravity is a massless spin-
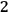 field), while the third gives a measure of how much the geometry of
field), while the third gives a measure of how much the geometry of
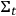 would change if the point were infinitesimally “pushed” toward a neighbouring
would change if the point were infinitesimally “pushed” toward a neighbouring
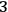 -surface
-surface
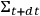 . In this sense, this third piece of information generates a notion of “forward in time” which is hidden in the geometry of a
. In this sense, this third piece of information generates a notion of “forward in time” which is hidden in the geometry of a
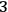 -surface. Thus, the Wheeler-DeWitt equation accounts for static universal configurations of “all elements of physical reality”: what these elements of reality should be and how the theory should single out a wave function from them is still an open question.
-surface. Thus, the Wheeler-DeWitt equation accounts for static universal configurations of “all elements of physical reality”: what these elements of reality should be and how the theory should single out a wave function from them is still an open question.
The main problem in this context is that Bohmian mechanics is not Lorentz-invariant.21 Consequently, it breaks the diffeomorphism invariance of general relativity. Thus, in non-relativistic Bohmian mechanics, if one had complete knowledge of the positions of the particles, that knowledge would reveal a preferred foliation of spacetime. However, since one cannot have complete knowledge of the positions of Bohmian particles (given that any measurement changes the positions of the particles), it is also in Bohm's theory not possible to send signals with a superluminal velocity and to know the objective, globally preferred foliation of spacetime.
In standard textbooks from von Neumann 1932 on, quantum mechanics is presented in the form of a combination of two radically different dynamics: when no measurement takes place, one uses the Schrödinger equation to calculate the temporal development of the wave function of a quantum system. However, when a measurement is made, the wave function is supposed to collapse so that it represents the system as having one determinate value of the measured property at the exclusion of all the other ones. Textbook quantum mechanics thus rejects proposition 1B above: the wave function completely describes the properties of physical systems, but under some circumstances—measurements being a case in point—quantum systems change in such a way that they acquire a determinate value of dynamical properties, that change being represented by the collapse of the wave function. Is it possible to make this idea precise so that one specifies when (under what circumstances) and how this change happens? Doing so requires amending the Schrödinger equation. The only precise physical proposal in this sense goes back to Ghirardi, Rimini and Weber Ghirardi et.al. 1986 (GRW). GRW add a stochastic term to the Schrödinger equation such that, in brief, a single microscopic quantum system has a very low objective probability to undergo a spontaneous localization. However, when one considers a macroscopic system that is composed of a huge number of microscopic quantum systems, one of these microscopic systems will immediately undergo a spontaneous localization so that, due to the entanglement, the whole system will be localized. When one couples a quantum system to a macroscopic system, due to the quantum system thus becoming entangled with the huge number of quantum systems making up the macroscopic system, it will also undergo a spontaneous localization very rapidly.
Nonetheless, it remains to be spelled out what exactly in the physical world the GRW dynamics represents, in other words, what the ontology of the GRW theory is. Taking textbook quantum mechanics literally, we have to say that a quantum system such as an electron, when not having a determinate value of position, is smeared out in space. What the GRW dynamics then achieves in improving on the collapse postulate in the textbooks is to describe how this position distribution, which is smeared out in
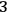 -dimensional physical space, develops into rather determinate values. This is indeed the reading of the physical significance of the GRW dynamics that Ghirardi et.al. 1995 themselves favor in proposing a mass density ontology: the mass of, say, an electron when it has not a determinate position is literally smeared out in physical space, creating thus a mass density field. However, the mass density ontology, like Bohmian mechanics, is not Lorentz-invariant.
-dimensional physical space, develops into rather determinate values. This is indeed the reading of the physical significance of the GRW dynamics that Ghirardi et.al. 1995 themselves favor in proposing a mass density ontology: the mass of, say, an electron when it has not a determinate position is literally smeared out in physical space, creating thus a mass density field. However, the mass density ontology, like Bohmian mechanics, is not Lorentz-invariant.
But there is another reading of the GRW dynamics possible. That reading is due to Bell 1987, 205. A good way to access it is via a comparison with Bohmian mechanics: in Bohm's theory, quantum systems always have a determinate position, and the determinate value of position is not taken into account in the wave function description. According to what is known as the GRW flash theory, quantum systems have a determinate value of position only when the wave function as developing according to the GRW modification of the Schrödinger dynamics indicates such a value (that is, when a spontaneous localization occurs), and these sparse determinate positions are all there is in the world. To put it differently, the spontaneous localizations that GRW postulate are conceived as flashes centred around spacetime points, and these flashes are all there is in spacetime. Starting with an initial distribution of flashes, the wave function is a tool to calculate the probabilities for the occurrence of further flashes.
The flash ontology is such that its dynamics can be formulated in a Lorentz-invariant manner, since it abandons the idea of continuous trajectories of anything in spacetime (such as Bohmian particles or field values, or mass densities in Ghirardi's ontology for GRW). Even if one had exact and complete knowledge of the flash distribution, one could not infer from that knowledge an objective foliation of spacetime.22 More precisely, it is the only worked out proposal for an interpretation of what quantum mechanics (or quantum field theory for that matter) tells us about the dynamics of matter in four-dimensional spacetime that has the chance of being Lorentz-invariant (the chance, since the formulation of Tumulka 2006 does not take interacting fields into account).
Both Bohm's theory and the GRW theory—on the mass density version as well as on the flash version—solve the measurement problem by accepting positions of something in spacetime (be it particles, be it field values, be it events such as flashes, be it the density of stuff) as primitive.23 In other words, they accept what John Bell calls “local beables” as primitive,24 differing in the local beables that they pose. On this basis, they then can account for definite positions of macroscopic systems in spacetime and thus retain proposition 1C (and 1C*). However, when it comes to quantum gravity, the problem is that the presupposition of accepting positions of something in spacetime as primitive can no longer be taken for granted, since the very concept of spacetime breaks down starting from the ADM formalism. If we take equations (16) as acting on a universal wave function, then the only thing we can talk about are
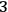 -geometries (possibly coupled with matter fields) as a whole, which means that we are not dealing anymore with something happening in spacetime but with universal timeless spatial configurations. Thus, in the “extreme” timeless interpretation25 of (16), we could have, for example, “flashes” in the configuration space (whatever this would mean), but surely not in spacetime. Moreover, even if we could find a suitable interpretation of (16) that permits us to talk about (partial) observables at the Planck scale, still those observables would not be in spacetime but, rather, they would constitute the very fabric of it.26 Let us therefore look into positions that solve the measurement problem by abandoning 1C.
-geometries (possibly coupled with matter fields) as a whole, which means that we are not dealing anymore with something happening in spacetime but with universal timeless spatial configurations. Thus, in the “extreme” timeless interpretation25 of (16), we could have, for example, “flashes” in the configuration space (whatever this would mean), but surely not in spacetime. Moreover, even if we could find a suitable interpretation of (16) that permits us to talk about (partial) observables at the Planck scale, still those observables would not be in spacetime but, rather, they would constitute the very fabric of it.26 Let us therefore look into positions that solve the measurement problem by abandoning 1C.
4 The Everett Interpretation
If one rejects 1C (and thus 1C*), one can regard the wave function as providing a complete description of the properties of physical systems (1A) and one does not have to amend the dynamics (1B). However, one has to replace 1C with an account of how it comes about that it seems to observers that there are determinate values of properties of themselves (their consciousness and their body) as well as their environment. In order to achieve such an account, it is common to draw on decoherence. Although decoherence does not lead to less, but to more entanglement, the quantum system becoming entangled with all the systems in its environment, the wave function of the whole system (quantum system and environment) rapidly develops in such a way that the superposed correlations do not interfere with each other. As far as the formalism of quantum mechanics is concerned, decoherence hence means a development of the wave function (or state vector or density matrix) in a high-dimensional mathematical space such that the interference terms between the superposed correlations vanish. The crucial issue then is to work out an answer to the question of how to get from this development of wave functions in a mathematical space to observers to whom determinate values of dynamical properties appear. Taking simply for granted that such observers somehow emerge out of or supervene on wave functions in a high-dimensional mathematical space evidently does not do the job of a precise physical account.
The only account available in the literature is of the following type: the physical significance of the vanishing of the interference terms between the superposed correlations is that decoherence induces a splitting or a branching of the universe into many non-interfering branches such that each of the superposed correlations constitutes at least one branch of the universe. Each of these branches that emerge due to decoherence constitutes a quasi-classical world. Thus, there is one branch in which the electron has spin up, the measuring device indicates spin up and the observer is conscious of the measuring device indicating spin up; and there is another branch in which the same electron has spin down, the same measuring device indicates spin down and the same observer is conscious of the measuring device indicating spin down. Since there are many measurements for which there are infinitely many possible outcomes—position measurements are a case in point—, this view is committed to maintaining that decoherence leads to the emergence of infinitely many branches. This position is therefore known as the many worlds interpretation of quantum mechanics, going back to Everett 1957.27
However, this proposal leaves a number of questions open. If the idea is that whenever there is decoherence, the whole physical universe develops into many branches, this means that each system in the universe—including its mass, its charge, etc.—is many times copied; but it is unclear how such a physical multiplication of mass and charge could be brought about. Furthermore, it is unclear whether or not the branching concerns spacetime itself. If it did not include spacetime, contradictory predicates would apply to one and the same spacetime region, or even contradictory properties would be instantiated by one and the same spacetime region—such as a measuring device indicating spin up and the same measuring device indicating spin down existing in or being properties of the same unique spacetime region. One can avoid this consequence by conceiving the branching as concerning spacetime itself; but then one would have to develop a physically precise account of how spacetime itself can be many times duplicated whenever there is decoherence so that many superposed spacetimes come into being. Moreover, since the branching is supposed to affect instantaneously the whole of spacetime, it is unclear whether and how the branching could be Lorentz-invariant.28
Furthermore, decoherence is a process leading from superposed correlations with interference terms to the vanishing of interference. The account under consideration replies to the question of the physical significance of this process by maintaining that many branches of the universe come into being that do not interfere with each other. But what is the physical significance of the entangled state of the universe prior to the emergence of the branches? Does this state consist in objects being smeared out in spacetime that upon decoherence get split up into all their possible determinate values of position in different branches of the universe? Kiefer 2004, ch. 10, sec. 10.1.2 tries to give a formal account of the appearance of global spacetime variables, such as time itself, from a quantum cosmological context. He summarizes the results as follows:
The lesson to be drawn is thus that the universe can appear classically only if experienced from within. A hypothetical “outside view” would only see a static quantum world. The most natural interpretation of quantum cosmology is an Everett-type interpretation, since the “wave function of the universe” contains by definition all possible branches. As macroscopic observers, however, we have access only to a tiny part of the cosmological wave function—the robust macroscopic branch which we follow. (Ibid., 318)
Kiefer's approach rests on an approximation technique similar to the so called “Born-Oppenheimer approximation.”29 The basic idea is to decompose the “universal” wave-function
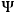 in (16) as follows:
in (16) as follows:
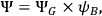
|
17 |
where
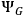 describes the full gravitational field and
describes the full gravitational field and
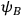 accounts for the remaining non-gravitational degrees of freedom. Very loosely speaking, this decomposition introduces a picture of the universe where a timeless “global” part generates the dynamical evolution of a “local” part representing the various branches. However, we must be very careful when drawing any conclusion from (17) for the simple reason that it is just an approximation and, hence, a light-hearted metaphysical reading of it might mislead us to consider as real features what are just artifacts of the mathematical manipulation of (16).
accounts for the remaining non-gravitational degrees of freedom. Very loosely speaking, this decomposition introduces a picture of the universe where a timeless “global” part generates the dynamical evolution of a “local” part representing the various branches. However, we must be very careful when drawing any conclusion from (17) for the simple reason that it is just an approximation and, hence, a light-hearted metaphysical reading of it might mislead us to consider as real features what are just artifacts of the mathematical manipulation of (16).
An even more counter-intuitive—and worrisome—account for the emergence of classical properties is Barbour's (Sakurai 1994, 474) approach. The most important physical entity for him is the “reduced” configuration space
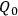 found by solving the diffeomorphism constraint in (16). Once this space has been found, the Hamiltonian constraint can be interpreted as giving a probability distribution over it. The important point is that there are not many possible probability distributions, but only one which is fixed in some way by the structure of the reduced configuration space, which means that there is no Hilbert space of wave functions. Each point in
found by solving the diffeomorphism constraint in (16). Once this space has been found, the Hamiltonian constraint can be interpreted as giving a probability distribution over it. The important point is that there are not many possible probability distributions, but only one which is fixed in some way by the structure of the reduced configuration space, which means that there is no Hilbert space of wave functions. Each point in
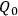 is a moment or a “now,” in the sense that it represents a universal static configuration. This framework calls for an Everett-type interpretation because it involves many “nows,” viz. many static pictures of the universe.30 How can we accommodate in the first place our experience of a time in a such static framework? The answer involves the concept of a “time capsule” which is a “static configuration of part or all the universe containing structures which suggest they are mutually consistent records of processes that took place in a past in accordance with certain laws” Barbour 1994b, 2884. A time capsule, then, is a point in
is a moment or a “now,” in the sense that it represents a universal static configuration. This framework calls for an Everett-type interpretation because it involves many “nows,” viz. many static pictures of the universe.30 How can we accommodate in the first place our experience of a time in a such static framework? The answer involves the concept of a “time capsule” which is a “static configuration of part or all the universe containing structures which suggest they are mutually consistent records of processes that took place in a past in accordance with certain laws” Barbour 1994b, 2884. A time capsule, then, is a point in
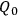 with an associated peak in the probability distribution. But probability of what? It seems that Barbour interprets the wave function as giving the probability for a “now” to be experienced. In his words:
with an associated peak in the probability distribution. But probability of what? It seems that Barbour interprets the wave function as giving the probability for a “now” to be experienced. In his words:
The timeless wavefunction of the universe concentrates the quantum mechanical probability on static configurations that are time capsules, so that the situations which have the highest probability of being experienced carry within them the appearance of time and history. Barbour 1999, 30
This interpretation reintroduces some sort of link between wave function and observer in a somewhat Copenhagen-like fashion. However, this immensely complicates the matter because, in addition to the strange fact that a mathematical object as the wave function “selects” what elements of
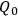 are to be experienced, we have to give a further account of how the observer “experience” occurs, i. e. how a static “brain configuration” embedded in a universal “now” generates the awareness of change in time. In short, it seems that the cure is much worse than the disease.
are to be experienced, we have to give a further account of how the observer “experience” occurs, i. e. how a static “brain configuration” embedded in a universal “now” generates the awareness of change in time. In short, it seems that the cure is much worse than the disease.
Conclusion: A Dilemma
If quantum gravity is to be a fundamental physical theory, it has to include an account of how to get from the entities that are posed as fundamental to classical phenomena such as measurement outcomes, since the evidence for a physical theory consists in measurements. However, as we have argued in this paper, setting out to do so runs into a dilemma: if one endorses a commitment to there really being classical properties (and thus definite measurement outcomes) in the world, accepting proposition 1C (and 1C*) above, then the only worked out accounts available presuppose positions in space or spacetime—of particles, field entities, events such as flashes, or density of stuff—as primitive. However, quantum gravity calls into question such primitives. As we have seen, in the formal process of building a theory of quantum gravity starting from the ADM formulation of GR and ending up with equations (16), the room for accommodating classical properties dramatically shrinks. Already in the classical regime the very notion of spacetime is weakened and eventually disappears in the quantum transition. From this point of view, the “problem of time” in QG is just the tip of the iceberg of a general collapse of the picture given by textbook quantum mechanics.31 Equations (16), taken at face value, tell us a strange tale of a frozen dynamics of blocks of universal
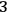 -geometries, where the notions of measurement and observable are put in jeopardy: is the wave function of the universe related to measurement outcomes? And what would be the physical meaning of setting up such a measurement? Even the best worked out attempts to recover more familiar notions from this picture (as in LQG, in the first place) cannot do much but end up dealing with quanta of area and volume or other physical entities that are alien to the notion of “position in space at a given time.” But if one abandons the commitment to there really being classical properties (and thus definite measurement outcomes) in the world, thus dropping proposition 1C (and 1C*) above, there is no clear strategy available as to how to account for the appearance of a classical world to observers:
at the present time, the formally best worked out accounts either involve questionable assumptions (e.g. approximations) or provide partial and unconvincing explanations. However, a literal reading of (16), such as Barbour's, makes it extremely difficult to find an account of the emergence of the classical world. The hope is that from a better understanding of (16) will follow a solution to the dilemma.
-geometries, where the notions of measurement and observable are put in jeopardy: is the wave function of the universe related to measurement outcomes? And what would be the physical meaning of setting up such a measurement? Even the best worked out attempts to recover more familiar notions from this picture (as in LQG, in the first place) cannot do much but end up dealing with quanta of area and volume or other physical entities that are alien to the notion of “position in space at a given time.” But if one abandons the commitment to there really being classical properties (and thus definite measurement outcomes) in the world, thus dropping proposition 1C (and 1C*) above, there is no clear strategy available as to how to account for the appearance of a classical world to observers:
at the present time, the formally best worked out accounts either involve questionable assumptions (e.g. approximations) or provide partial and unconvincing explanations. However, a literal reading of (16), such as Barbour's, makes it extremely difficult to find an account of the emergence of the classical world. The hope is that from a better understanding of (16) will follow a solution to the dilemma.
References
Albert, D.Z. (1992). Quantum Mechanics and Experience..
Allori, V., S. Goldstein, S. G., Tumulka S. (2008). On the common structure of Bohmian mechanics and the Ghirardi-Rimini-Weber theory. British Journal for the Philosophy of Science 59: 353-389
Arnowitt, R., S. Deser, S. D. (2004). The Dynamics of General Relativity. arXiv:gr-qc/0405109v1
Ashtekar, A. (1986). New variables for classical and quantum gravity. Physical Review Letters 57: 2244-2247
Barbour, J.B. (1994a). The Timelessness of Quantum Gravity: I. The Evidence from the Classical Theory. Classical and Quantum Gravity 11: 2853-2873
- (1994b). The Timelessness of Quantum Gravity: II. The Appearance of Dynamics in Static Configurations. Classical and Quantum Gravity 11: 2875-2897
- (1999). The End of Time. The Next Revolution in Physics..
Barrett, J.A. (1999). The Quantum Mechanics of Minds and Worlds..
Bell, J.S. (1987). Speakable and Unspeakable in Quantum Mechanics..
Bohm, D. (1952). A suggested interpretation of the quantum theory in terms of “hidden” variables. Physical Review 85: 166-193
Bohm, D., B. Hiley (1993). The Undivided Universe. An Ontological Interpretation of Quantum Theory..
Dirac, P.A.M. (1958). The theory of gravitation in Hamiltonian form. Proceedings of the Royal Society A 246: 333-343
- (1964). Lectures on Quantum Mechanics..
Dürr, D., S. Goldstein, S. G., Tumulka S. (2005). Bell-type quantum field theories. Journal of Physics A 38: R1-R43
Dürr, D., S. Goldstein, S. G. (2004). Bohmian mechanics and quantum field theory. Physical Review Letters 93: 090402
Everett, H. (1957). “Relative state” formulation of quantum mechanics. Reviews of Modern Physics 29: 454-462
Ghirardi, G.C., R. Grassi, R. G. (1995). Describing the macroscopic world: Closing the circle within the dynamical reduction program. Foundations of Physics 25: 5-38
Ghirardi, G.C., A. Rimini, A. R. (1986). Unified dynamics for microscopic and macroscopic systems. Physical Review D 34: 470-491
Goldstein, S. (2009). Bohmian Mechanics. In: The Stanford Encyclopedia of Philosophy Ed. by Edward N. Zalta.
Goldstein, S., S. Teufel (2001). Quantum Spacetime without Observers: Ontological Clarity and the Conceptual Foundations of Quantum Gravity. In: Physics Meets Philosophy at the Planck Scale Ed. by C. Callender, N. Hugget. 275-289
Green, M.B., J.H. Schwarz (1984). Anomaly cancellation in supersymmetric . Physics Letters B 149: 117-122
Green, M.B., J.H. Schwarz, J. S. (1987). Superstring Theory..
Henneaux, M., C. Teitelboim (1992). Quantization of Gauge Systems..
Kiefer, C. (2004). Quantum Gravity..
Kuchar̆, K. (1992). Time and interpretations of quantum gravity. In: 4 Ed. by G. Kunstatter, D.E. Vincent, D. V.. 211-314
- (1993). Canonical quantum gravity. In: General Relativity and Gravitation Ed. by R.J. Gleiser, C.N. Kozameh, C. K.. 119-150
Maudlin, T. (1995). Three measurement problems. Topoi 14: 7-15
- (2011). Quantum Non-locality and Relativity..
Rosenfeld, L. (1930). Über die Gravitationswirkungen des Lichtes. Zeitschrift für Physik 65: 589-599
Rovelli, C. (2002). Partial Observables. Physical Review D 65(12): 124013
- (2004). Quantum Gravity..
- (2007). Quantum Gravity. In: Philosophy of Physics Ed. by J. Butterfield, J. Earman. Handbook of the Philosophy of Science.
Rovelli, C., L. Smolin (1990). Loop space representation of quantum general relativity. Nuclear Physics B 331: 80-152
Sakurai, J.J. (1994). Modern Quantum Mechanics. Revised Edition..
Saunders, S., J.A. Barrett, J. B., Kent J.A. (2010). Many Worlds? Everett, Quantum Theory, and Reality..
Tumulka, R. (2006). A relativistic version of the Ghirardi-Rimini-Weber model. Journal of Statistical Physics 125: 821-840
von Neumann, J. (1932). Mathematische Grundlagen der Quantenmechanik..
Wallace, D. (2010). Decoherence and ontology (or: How I learned to stop worrying and love FAPP). In: Many Worlds? Everett, Quantum Theory, and Reality Ed. by S. Saunders, J.A. Barrett, J. B., Kent J.A.. 54
Footnotes
See, e.g., (Green and Schwarz 1984; Green et.al. 1987).
See, e.g., Green et.al. 1987.
See, e.g., Rovelli 2007.
Dotted quantities symbolize a derivative with respect to a suitably chosen real parameter. In the case of a classical system the most obvious choice is the usual Newtonian time
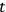 . Moreover, from now on, we will always assume that the subscript
. Moreover, from now on, we will always assume that the subscript
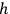 ranges from 1 to
ranges from 1 to
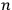 .
.
Here and throughout the text we set
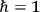 .
.
The following treatment of constrained Hamiltonian systems is absolutely not rigorous and serves merely heuristic purposes. For an exhaustive treatment of such topics see, e.g., Henneaux and Teitelboim 1992.
Just to be a little bit more precise, this happens when
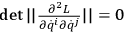 , with
, with
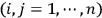 .
.
We will later refer to this feature as “diffeomorphism invariance.” Albeit they are not the same thing, here we can harmlessly blur the distinction.
The problem of time that we are going to spell out in a moment rests on the fact that this “temporal” degree of freedom turns out to be unphysical.
See, e.g., Kiefer 2004, ch. 3, sec. 3.1.
This is why we still do not have a completely worked out canonical theory of QG.
To avoid the quicksand of the substantivalism vs relationism debate, we will consider this way of speaking equivalent to saying “empty spacetime” without further elaboration.
Obviously, this choice dramatically cuts out the number of models of GR that can be described by this formalism: all spacetimes that do not admit a global time function are disregarded.
The global hyperbolicity conditions assures the existence of such a function.
Not always captured: there are cases in which the Hamiltonian description of a general relativistic system fails to encode the diffeomorphic invariance of GR. However, we do not need to worry about this issue here.
More precisely, if
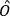 is such an operator, then it must be
is such an operator, then it must be
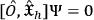 .
.
See, in particular, Bell 1987, ch. 19.
See, e.g., Kuchar̆ 1992.
See Albert 1992, 155–161, for a nice illustration why this is so.
See Tumulka 2006 and Maudlin 2011, ch. 10.
See Allori et.al. 2008 for an illuminating comparison of the ontologies of Bohm, GRW mass density and GRW flash.
See Bell 1987, ch. 7.
For a paradigmatic example of such an interpretation see, e.g., Barbour 1999. In the next section, we will see in slightly more detail some consequences of this interpretation.
See, e.g., Rovelli 2004, ch. 1, sec. 1.2.2.
See Wallace 2010 for a concise statement and, in general, the papers in Saunders et.al. 2010.
See, e.g., Sakurai 1994, 474 for a brief technical treatment.
This way of speaking can be misleading: here the picture is the universe, so each “now” represents a distinct universe.
For example, the usual account of unitarity as the fact that the probabilities associated to the possible outcomes of a given experiment must add up to unity at a fixed time is obviously problematic in QG.
