Abstract. The paper presents a “therapeutic” account of quantum theory, the “Rule Perspective,” which attempts to dissolve the notorious paradoxes of measurement and non-locality by reflection of the nature of quantum states. The Rule Perspective is based on the epistemic conception of quantum states—the view that quantum states are not descriptions of quantum systems but rather reflect the assigning agents' epistemic relations to the systems. The main attractions of this conception of quantum states are outlined before it is spelled out in detail in form of the Rule Perspective. The paper closes with an assessment of the status of quantum probabilities in the light of the considerations presented before.
1 Introduction
By most accounts, the measurement problem and the problem of quantum “non-locality,” that is, the tension between quantum theory and relativity theory, are the two most important challenges in the foundations of quantum mechanics. Possible ways to react to these problems range from changing the dynamics (as in GRW theory) to adding determinate particle and field configurations (as in pilot wave approaches) to adopting a non-standard metaphysical picture in which the universe continuously splits up in an immense number of branches (the Everett interpretation). A completely different approach to the solution of the two problems is to try to dissolve them by showing that they arise from misunderstandings of the notions in terms of which quantum theory is formulated and disappear as soon as these misunderstandings are removed. Such a perspective on the quantum mechanical formalism is offered by the epistemic conception of states—the view that quantum states do not describe the properties of quantum systems but rather reflect the state-assigning agents' epistemic relations to the systems. The main attraction of this idea is that it offers a reading of the quantum mechanical formalism that avoids both the measurement problem and the problem of quantum non-locality in a very elegant way.1
There are two very different types of accounts that are based on the epistemic conception of states. Those of the first type are hidden variable models where the quantum state expresses incomplete information about the configuration of hidden variables that obtains in that any configuration of hidden variables (which one might call an “ontic” state) is compatible with several quantum states, which one might therefore characterize as “epistemic.”2 In this paper, I will only talk about accounts of a second, very different type. Accounts of this second type try to dissolve the paradoxes of measurement and non-locality without presenting a theory of “ontic” states of quantum systems at all. They can be characterized as “interpretation[s] without interpretation”3 in the sense that, according to them, quantum theory is fine as it stands without any additional technical vocabulary such as hidden variables, branching worlds, dynamics of collapse, or whatever else. Such a perspective on quantum theory can be called “therapeutic” in that it holds the promise to “cure” us from what is seen as unfounded worries about foundational issues like the measurement problem on the basis of conceptual clarification alone.
The question of whether this promise can be fulfilled will be discussed in this paper, beginning in Section 2, where I briefly review the dissolutions of the paradoxes of measurement and non-locality offered by the epistemic conception of states. Sections 3 and 4 present a more specific account, which I propose to call the “Rule Perspective,” that fleshes out the basic idea of the epistemic conception of states in more detail. Subsequently, Section 5 assesses the status of quantum probabilities in the light of the considerations presented before. The paper closes in Section 6 with a short remark on why the Rule Perspective, despite being based on a reading of quantum states as non-descriptive, is not a form of instrumentalism in that it presupposes rather than denies that physical states of affairs are describable in objective (yet non-quantum) terms.
2 Dissolving the Paradoxes
The measurement problem arises from the fact that if quantum states are seen as states that quantum systems “are in,” evolving in time always according to the Schrödinger equation, measurements rarely have outcomes.4 In quantum theoretical practice, the problem is solved “by brute force,” namely, by invoking von Neumann's notorious projection postulate, which claims that the state of the measured system “collapses” to an eigenstate of the measured observable whenever a measurement is performed. Measurement collapse is commonly criticized on two grounds, first, that it is in stark contrast to the smooth time-evolution according to the Schrödinger equation in that it is abrupt and unphysical and, second, that we are given no clear criteria for distinguishing between situations where time-evolution follows the Schrödinger equation on the one hand and situations where collapse occurs on the other.5
The dissolution of the measurement problem in the epistemic conception of states has two different aspects: First, a conceptual presupposition for formulating the measurement problem is rejected by denying that quantum states describe the properties of quantum systems in the sense that the very idea of quantum states as states that quantum systems “are in” is not accepted. This makes it impossible to argue, as in standard expositions of the measurement problem, that according to the law of quantum mechanical time-evolution the measured observable cannot have a determinate value in the state the measured system is in. Second, the epistemic conception of states offers a very natural justification of measurement collapse by means of which the measurement problem is avoided in quantum mechanical practice. If one accepts the idea that quantum states in general depend on the assigning agent's epistemic situations with respect to the systems that the states are assigned to, the collapse of the wave function appears completely natural in that it merely reflects a sudden and discontinuous change in the epistemic situation of the assigning agent, not a mysterious discontinuity in the time-evolution of the properties of the system itself. The epistemic conception of states thus removes the inconsistency of the standard, ontic, perspective on quantum states with the fact that measurements evidently do have outcomes. It does not somehow explain the emergence of determinate outcomes but attempts to cause the felt need for a dynamical explanation of these to vanish. I shall briefly return to how this is done in the Rule Perspective at the end of Section 5.
To see the dissolution of the “paradox of quantum non-locality,” that is, the difficulty of reconciling quantum mechanical time-evolution in the presence of collapse with the requirement of Lorentz covariance as imposed from relativity theory,6 it is useful to consider as a specific example a two-particle system in an EPR-Bohm setup where two systems
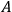 and
and
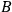 are prepared in such a way that those knowing about the preparation procedure assign an entangled state, for instance, the state
are prepared in such a way that those knowing about the preparation procedure assign an entangled state, for instance, the state
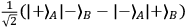 , for the combined spin degrees of freedom. The two systems
, for the combined spin degrees of freedom. The two systems
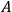 and
and
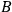 are brought far apart and an agent, Alice, located at the first system, measures its spin in a certain direction. Having registered the result, she assigns two no longer entangled states to
are brought far apart and an agent, Alice, located at the first system, measures its spin in a certain direction. Having registered the result, she assigns two no longer entangled states to
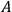 and
and
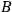 , which depend both on the choice of observable measured and on the measured result. Another agent, Bob, located at the second system, may also perform a spin measurement (in the same or in a different direction of spin) and proceed to assign a pair of no longer entangled states to the two systems in an analogous way. Now the intriguing challenge for the ontic conception of quantum states as states quantum systems “are in” is to specify at which time which system is in which state and, in order to preserve compatibility with relativity theory, to do so in a Lorentz covariant manner. The difficulty is most pressing for cases where the measurements carried out by Alice and Bob occur in space-like separated regions, perhaps even in such a way that each of them precedes the other in its own rest frame.7 In that case there is clearly no non-arbitrary answer to the question of which measurement occurs first and triggers the abrupt change of state of the other. Existing attempts to overcome this problem make quantum mechanical time-evolution dependent on foliations of spacetime into sets of parallel hyperplanes, but so far no such approach has found widespread acceptance.8
, which depend both on the choice of observable measured and on the measured result. Another agent, Bob, located at the second system, may also perform a spin measurement (in the same or in a different direction of spin) and proceed to assign a pair of no longer entangled states to the two systems in an analogous way. Now the intriguing challenge for the ontic conception of quantum states as states quantum systems “are in” is to specify at which time which system is in which state and, in order to preserve compatibility with relativity theory, to do so in a Lorentz covariant manner. The difficulty is most pressing for cases where the measurements carried out by Alice and Bob occur in space-like separated regions, perhaps even in such a way that each of them precedes the other in its own rest frame.7 In that case there is clearly no non-arbitrary answer to the question of which measurement occurs first and triggers the abrupt change of state of the other. Existing attempts to overcome this problem make quantum mechanical time-evolution dependent on foliations of spacetime into sets of parallel hyperplanes, but so far no such approach has found widespread acceptance.8
If one adopts the epistemic conception of quantum states, the problem of reconciling quantum theory and relativity theory disappears and the sudden change of the state Alice assigns to the second system appears very natural: Alice knows about the preparation procedure for the combined two-particle system, and it is not surprising that the result of her measurement of the first system may affect her epistemic condition with respect to the other. By interpreting the state not as a description of the system itself but as reflecting her epistemic situation we need not assume that her measurement of the first system has a physical effect on the second. Predictions for the results of measurement that are derived on the basis of entangled states may still be baffling and unexpected, but no conflict with the principles of relativity theory in form of superluminal effects on physical quantities does arise. Even though quantum mechanics is non-local in the sense of violating Bell-type inequalities, it does not involve any superluminal propagation of objective properties.
3 Quantum Bayesianism and Its Problems
In the previous sketch of the dissolution of the paradoxes of measurement and non-locality the question of in which sense quantum states may be regarded as reflecting the epistemic conditions of the assigning agents was not answered. Sometimes the epistemic conception of states is read as the claim that a quantum state represents our knowledge of the probabilities ascribed to the values of observables determined from it via the Born rule. Marchildon, for instance, identifies that view with the epistemic conception of states when he claims that “[i]n the epistemic view [of states], the state vector (or wave function or density matrix) does not represent the objective state of a microscopic system [...], but rather our knowledge of the probabilities of outcomes of future measurements.”9 However, as has been convincingly argued by Fuchs,10 the notion of knowledge of quantum probabilities is incompatible with the epistemic conception of states, so the latter should evidently not be identified with the view described by Marchildon.
The reason why the notion of knowledge of quantum probabilities is incompatible with the epistemic conception of states has to do with the “factivity” of knowledge, that is, the conceptual feature of the notion of knowledge that knowing that
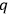 is possible only if
is possible only if
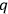 is indeed the case. As stressed above in the discussion of the dissolution of the measurement problem, the epistemic conception of states does not acknowledge the existence of a true state of a quantum system, a state it “is in.” According to this perspective, different agents having different knowledge of the values of observables of a quantum system may legitimately assign different quantum states to it. The idea that quantum states reflect the assigning agents' knowledge of quantum probabilities, however, is incompatible with the assumption that different agents may legitimately assign different states to one and the same system. For if indeed probabilities were the objects of the assigning agents' knowledge, an agent might know the probability
is indeed the case. As stressed above in the discussion of the dissolution of the measurement problem, the epistemic conception of states does not acknowledge the existence of a true state of a quantum system, a state it “is in.” According to this perspective, different agents having different knowledge of the values of observables of a quantum system may legitimately assign different quantum states to it. The idea that quantum states reflect the assigning agents' knowledge of quantum probabilities, however, is incompatible with the assumption that different agents may legitimately assign different states to one and the same system. For if indeed probabilities were the objects of the assigning agents' knowledge, an agent might know the probability
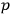 of a certain measurement outcome
of a certain measurement outcome
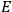 to occur, which would mean that, due to the factivity of “knowledge,”
to occur, which would mean that, due to the factivity of “knowledge,”
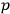 would be the one and only correct, the true probability for
would be the one and only correct, the true probability for
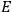 to occur. Since this holds for any possible measurement outcome
to occur. Since this holds for any possible measurement outcome
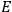 to which the state assigned to the system ascribes some probability
to which the state assigned to the system ascribes some probability
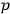 , the probabilities obtained from this state would be the true ones and any other assignment of probabilities that differs from an assignment of these would simply be wrong. This conclusion would be incompatible with the claim that the states assigned by different observers to the same quantum system may legitimately be different. Therefore, the epistemic conception of states cannot be spelled out by saying that quantum states reflect knowledge about probabilities.
, the probabilities obtained from this state would be the true ones and any other assignment of probabilities that differs from an assignment of these would simply be wrong. This conclusion would be incompatible with the claim that the states assigned by different observers to the same quantum system may legitimately be different. Therefore, the epistemic conception of states cannot be spelled out by saying that quantum states reflect knowledge about probabilities.
A viable (yet, as we shall see, too radical) option for adherents of the epistemic conception of states is to say that quantum states reflect the assigning agents' subjective degrees of belief about possible measurement outcomes. An account, which is based on this idea, has been worked out in great detail by Fuchs, Caves, and Schack and is now widely known as quantum Bayesianism. According to Fuchs, quantum states reflect our beliefs about what the results of “our interventions into nature”11 might be. The probabilities encoded in quantum states, from this perspective, are not the objects of the beliefs reflected in these states, but they measure the degrees to which the agents assigning the states believe that the measurement outcomes will occur.
Since degrees of belief may differ from agent to agent without any of them necessarily making any kind of mistake, quantum Bayesianism does not encounter the same problems as the view that quantum states represent our knowledge of probabilities. It does, however, have a drawback in that it goes extremely far in characterizing elements of the quantum mechanical formalism as subjective in order to be consistent as an epistemic account of states. The most radical feature of quantum Bayesianism, arguably, is its denial of the fact that, for any given measurement setup, the question of which observable is measured in that setup might have a determinate answer. Fuchs argues as follows for this view:
Take, as an example, a device that supposedly performs a standard von Neumann measurement, the measurement of which is accompanied by the standard collapse postulate. Then when a click
is found, the posterior quantum state will be
regardless of the initial state
. If this state-change rule is an objective feature of the device or its interaction with the system—i. e., it has nothing to do with the observer's subjective judgement—then the final state must be an objective feature of the quantum system. Fuchs 2002, 39
Fuchs' main point seems to be that if a set
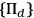 of projection operators is objectively associated to a given experimental setup, registering a “click
of projection operators is objectively associated to a given experimental setup, registering a “click
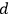 ” means that the state to be assigned after measurement is
” means that the state to be assigned after measurement is
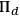 independently of which state
independently of which state
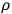 has been assigned to the system before. The post-measurement state seems to be fixed and we seem to have ended up with a true post-measurement state
has been assigned to the system before. The post-measurement state seems to be fixed and we seem to have ended up with a true post-measurement state
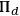 —a result which is incompatible with the epistemic conception of states. Therefore, it seems that the question of which observable is measured in which experimental setup can have no determinate answer according to the epistemic conception of states.
—a result which is incompatible with the epistemic conception of states. Therefore, it seems that the question of which observable is measured in which experimental setup can have no determinate answer according to the epistemic conception of states.
This conclusion, however, is extremely difficult to swallow. If sound, one could legitimately regard it as a reductio of the idea that the foundational problems of quantum theory can be dissolved by the epistemic conception of states. In actual quantum mechanical practice experimentalists agree almost always on which observable is measured by which device, and quantum mechanics could hardly be as empirically successful as it is if this were not the case. Furthermore, if measurement could never be regarded as measurement of a determinate observable in any given context, it would not make any sense to ask for any measured value to which observable it belongs. Knowledge of the values of observables would be excluded as a matter of principle, for one could never decide which observable some given value is a value of. Quantum mechanical practice, however, clearly seems to presuppose that we often do have knowledge of the values of at least some observables, and even if one adopts the radical position that microscopic observables (however one actually defines them) do never possess determinate values, this option is not available for the macroscopic systems to which we have more direct access but treat them quantum mechanically as many-particle systems by the methods of quantum statistical mechanics (e.g. when computing heat capacities, magnetic susceptibilities, and the like). At least approximate knowledge of macroscopic quantities, such as volume, particle number, temperature, pressure, and macroscopic magnetization is usually presupposed, and denying that such knowledge is possible seems not a promising option.
By claiming that the question of which observable is measured in which setup has no determinate answer quantum Bayesians consciously reject not only the notion of a quantum state a quantum system is in, but also the notion of a state assignment being performed correctly. While quantum Bayesians have successfully shown that the notion of a quantum state a quantum system is in can be avoided in a class of cases where it appears to be absolutely essential (in so-called “quantum state tomography”),12 they have not been able to establish an analogous argument for the dispensability of the notion of a state assignment being performed correctly. This notion, however, seems to play an essential role in quantum mechanical practice, for instance in the case of systems being prepared by a (so-called) state preparation device, where any state assignment that deviates from a highly specific one is counted as wrong by all competent experimentalists. State preparation can be described as a form of measurement in that only systems exhibiting values of an observable lying within a certain interval are allowed to exit the device on the “prepared states” path, so accepting the notion of a state assignment being performed correctly is equivalent to allowing the question of which observable is measured in which setup to have a determinate answer. In the following section, I present an account which fleshes out the notion of a state assignment being performed correctly without invoking the notion of a state a quantum system is in.
4 Constitutive Rules and State Assignment
The most promising strategy to make sense of the notion of a state assignment being performed correctly without relying on the notion of a state a quantum system is in is to argue that to assign correctly means to assign in accordance with certain rules governing state assignment.13 From the perspective of the epistemic conception of states one will have to think of these rules as determining the state an agent has to assign to the system depending on what she knows of the values of its observables. Examples of the rules according to which state assignment is performed are unitary time-evolution in accordance with the Schrödinger equation (which applies whenever no new information about measurement data comes in), Lüders' rule (a generalized version of the von Neumann projection postulate) for updating one's assignment of a quantum state in the light of new data, and the principle of entropy maximization, which is used in contexts where a state should be assigned to a system where none was assigned before. To understand the peculiar status which is ascribed to these rules in the epistemic account of states proposed here, it is useful to compare their role in the present account to their role in the standard—ontic—conception of quantum states as descriptions of quantum systems. In this context, a terminological distinction proposed by John Searle 1969 in his theory of speech acts is very useful for clarifying the differing roles of the rules of state assignment in ontic accounts of quantum states and in the epistemic account of states proposed here.
Searle introduces the distinction between the two types of rules as follows:
I want to clarify a distinction between two different sorts of rules, which I shall call regulative and constitutive rules. I am fairly confident about the distinction, but do not find it easy to clarify. As a start, we might say that regulative rules regulate antecedently or independently existing forms of behavior; for example, many rules of etiquette regulate inter-personal relationships which exist independently of the rules. But constitutive rules do not merely regulate, they create or define new forms of behavior. The rules of football or chess, for example, do not merely regulate playing football or chess, but as it were they create the very possibility of playing such games. The activities of playing football or chess are constituted by acting in accordance with (at least a large subset of) the appropriate rules. Regulative rules regulate pre-existing activity, an activity whose existence is logically independent of the rules. Constitutive rules constitute (and also regulate) an activity the existence of which is logically dependent on the rules. Searle 1969, 33f
The standard ontic conception of quantum states as states quantum systems are in conceives of the rules governing state assignment as regulative rules. This can be seen by noting that whenever an agent assigns a quantum state to a quantum system what she aims at, according to the ontic conception of states, is to assign the state in which the system really is (or at least some reasonable approximation to it). This goal, however, can be specified without relying in any way on the rules which the agent follows in order to achieve it. Consequently, from the perspective of ontic accounts of quantum states, the notion of a state assignment being performed correctly is “logically independent of the rules”14 according to which it is done. In these accounts, the role of the rules of state assignment is that of an instrument or a guide to determine the state the system really is in (or some reasonable approximation to it). From this perspective, state assignment can be characterized “antecedently [to] or independently” of the rules according to which it is performed. These rules are therefore conceived of as regulative rules in ontic accounts of quantum states.
In the epistemic account of quantum states proposed here, in contrast, the rules of state assignment play an entirely different role: They can be neither a guide nor an instrument for determining the state the system is in, for the notion of such a state is rejected. The basic idea, instead, is that to assign in accordance with the rules of state assignment is what it means to assign correctly, so the notion of a state assignment being performed correctly is itself defined in terms of these rules. It is therefore, as Searle writes, “logically dependent on the rules” according to which it is done, so these rules should be conceived of as constitutive rules in an epistemic account of states that preserves the notion of a state assignment being performed correctly without accepting the notion of a state a quantum system is in.
Having introduced the basic idea of the “Rule Perspective” as an epistemic account of quantum states that conceives of the rules of state assignment as constitutive rules, we can now come back to Fuchs' argument that there can be no determinate answer to the question of which observable is measured in which experimental setup. According to Fuchs, if the observable measured were an objective feature of the device, the measured result would impose objective constraints on the state to be assigned to the system after measurement, which he regards as in conflict with the basic idea of the epistemic conception of states that there is no agent-independent true state of the system. As I shall argue now, however, the epistemic account of states presented here is perfectly compatible with the view that the question of which observable is measured in an experimental setup has a determinate answer.
To see this, assume that the observable that is measured in a given experimental setup is an objective feature of the measuring device and that, in accordance with the Rule Perspective, the rules of state assignment require an agent having performed a measurement with that setup to assign some specific quantum state to the measured system in order to assign correctly. Does it follow from these assumptions that the state she has to assign to the system after measurement must be regarded as the state it really is in, in conflict with the epistemic conception of states? Clearly not: All that follows is that those agents who have obtained information about the registered result must update the states they assign to the system in accordance with Lüders' rule, taking into account the registered result. With regard to the case considered by Fuchs this means that those knowing that the “click
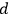 ” has been registered must update their states to
” has been registered must update their states to
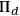 after measurement in order to assign correctly. To arrive at the further conclusion that
after measurement in order to assign correctly. To arrive at the further conclusion that
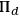 is the true state of the system one would have to demonstrate that assigning any other state than
is the true state of the system one would have to demonstrate that assigning any other state than
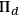 would amount to making a mistake, whatever one knows of the values of observables of the system. One would have to show, in other words, that assigning a state that is different from
would amount to making a mistake, whatever one knows of the values of observables of the system. One would have to show, in other words, that assigning a state that is different from
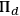 would be wrong not only for those who know that the “click
would be wrong not only for those who know that the “click
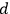 ” has been registered, but also for those who don't.
” has been registered, but also for those who don't.
This point is enforced by noting that there can be agents assigning states to the system who might not have had a chance to register the “click
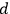 .” Registering it may have been physically impossible for them, for the process resulting in the “click
.” Registering it may have been physically impossible for them, for the process resulting in the “click
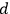 ” may be situated completely outside their present backward light cone. If we adhere to the discipline that the states assigned by these agents reflect their epistemic relations to the system, it makes no sense to hold that they ought to assign the state
” may be situated completely outside their present backward light cone. If we adhere to the discipline that the states assigned by these agents reflect their epistemic relations to the system, it makes no sense to hold that they ought to assign the state
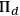 as well because, given their epistemic relations to the system, the rules of state assignment advise them to assign differently. According to the epistemic conception of states, their state assignments have to be adequate to their epistemic condition with respect to the system, so they would not only not be obligated to assign
as well because, given their epistemic relations to the system, the rules of state assignment advise them to assign differently. According to the epistemic conception of states, their state assignments have to be adequate to their epistemic condition with respect to the system, so they would not only not be obligated to assign
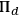 , it would even be wrong for them.
, it would even be wrong for them.
In the following section I discuss what ramifications the perspective on the rules of state assignment as constitutive rules has for the interpretation of quantum probabilities.
5 The Interpretation of Quantum Probabilities
Having considered the status of the rules of state assignment in the epistemic account of quantum states, which I have called the “Rule Perspective,” I now turn to the interpretation of probabilities derived from quantum states via the Born Rule. While quantum Bayesianism describes them as subjective degrees of belief in accordance with the personalist Bayesian conception of probability, the Rule Perspective ascribes to them a more objective character which is arguably better in agreement with their actual role in quantum theoretical practice.
The most important sense in which quantum probabilities remain subjective in the Rule Perspective is that, for the same observable and the same quantum system, they may differ from agent to agent without one of them making a mistake. Inasmuch as one regards any quantities exhibiting an agent dependence as subjective one will therefore conclude that the Rule Perspective classifies quantum probabilities as subjective. However, quantum probabilities as conceived by the Rule Perspective can be seen objective in other, no less important regards, for instance in that the question of which probability should be assigned by an agent to the value of an observable is regarded as having a determinate, objective answer whenever the epistemic situation of that agent is sufficiently specified. Depending on whether a state assignment is performed correctly, the probabilities computed from the state via the Born Rule are either correct or incorrect in an objective way.15
Quantum Bayesianism stresses the non-descriptive, normative character of quantum theory by arguing that “[i]t is a users [sic] manual that any agent can pick up and use to help make wiser decisions in this world of inherent uncertainty” Fuchs 2010, 8 and by claiming that the Born Rule imposes norms on how to form our beliefs as regards “the potential consequences of our experimental interventions into nature” Fuchs 2002, 7. The Rule Perspective agrees, but it adds that quantum theory not only provides us with norms of how to “make wiser decisions,” given the quantum states we have assigned to quantum systems, but also with norms of how to assign these states to the systems in the first place. The normative character which quantum theory has according to both quantum Bayesianism and the Rule Perspective is obscured by the formulation that quantum states are “states of belief,”16 which is sometimes found in the writings of quantum Bayesians. This formulation is misleading because it invites the reading that quantum states, instead of being descriptions of physical objects, are descriptions of agents and their beliefs. This would imply that an assignment of a quantum state to a quantum system by an agent would be adequate if and only if the probabilities derived from that state corresponded exactly to the agent's degrees of belief, for only under this condition can the state be said to correctly describe the agent's system of beliefs. It is clear, however, that if quantum Bayesianism takes seriously its own characterization of quantum theory as a normative “manual” to “make wiser decisions,” it need not regard quantum states as descriptions of anything, neither of the systems themselves nor of the assigning agents' degrees of belief. Much more naturally, it regards them as prescriptions for forming beliefs and for acting in the light of available information. According to this perspective, quantum states are not literally states of anything, neither of objects nor of agents.17
Having discussed the question in which sense quantum probabilities are subjective and in which sense they are objective, I now turn to the question of what quantum probabilities are probabilities of. To answer this question, the notion of a non-quantum magnitude claim—“NQMC” in what follows—is very useful, which has recently been introduced by Richard Healey in the context of his “pragmatist approach” (Healey forthcoming, forthcoming) to quantum theory, which is in many respects similar in spirit to the Rule Perspective. An NQMC is a statement of the form “The value of observable
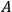 of system
of system
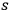 lies in the set of possible values
lies in the set of possible values
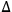 .” Healey refers to these statements as “non-quantum” since “NQMCs were frequently and correctly made before the development of quantum theory and continue to be made after its widespread acceptance, which is why [he calls] them non-quantum” (Healey forthcoming, forthcoming, 25). It is perhaps possible to identify NQMCs with what, for Heisenberg, were descriptions in terms of “classical concepts,”18 but Healey objects against this use of “classical” to avoid the misleading impression that an NQMC “carries with it the full content of classical physics.” Another plausible reason for not calling NQMCs “classical” is that some of them use non-classical concepts such as spin. According to the Rule Perspective, NQMCs are descriptively used in quantum mechanical practice, in contrast to quantum states.
.” Healey refers to these statements as “non-quantum” since “NQMCs were frequently and correctly made before the development of quantum theory and continue to be made after its widespread acceptance, which is why [he calls] them non-quantum” (Healey forthcoming, forthcoming, 25). It is perhaps possible to identify NQMCs with what, for Heisenberg, were descriptions in terms of “classical concepts,”18 but Healey objects against this use of “classical” to avoid the misleading impression that an NQMC “carries with it the full content of classical physics.” Another plausible reason for not calling NQMCs “classical” is that some of them use non-classical concepts such as spin. According to the Rule Perspective, NQMCs are descriptively used in quantum mechanical practice, in contrast to quantum states.
As I shall argue now, the notion of an NQMC is useful in answering the question what the probabilities derived from the Born Rule are probabilities of. The most straightforward reading of the Born Rule
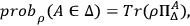
|
1 |
where
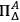 denotes the projection on the span of eigenvectors of
denotes the projection on the span of eigenvectors of
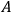 with eigenvalues lying in
with eigenvalues lying in
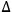 , is that it ascribes a probability to a statement of the form “The value of
, is that it ascribes a probability to a statement of the form “The value of
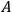 lies in
lies in
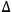 ,” that is, to an NQMC. This reading, however, is in need of further qualification in that, as the famous no-go results due to Gleason, Bell, Kochen, Specker, and others suggest, not all NQMCs can simultaneously have determinate truth values. A common reaction to this problem is to restrict the interpretation of the Born Rule to measurement outcomes, saying that the probabilities derived from it are to be understood as conditional on measurement of
,” that is, to an NQMC. This reading, however, is in need of further qualification in that, as the famous no-go results due to Gleason, Bell, Kochen, Specker, and others suggest, not all NQMCs can simultaneously have determinate truth values. A common reaction to this problem is to restrict the interpretation of the Born Rule to measurement outcomes, saying that the probabilities derived from it are to be understood as conditional on measurement of
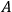 , and to deny that quantum theory has any empirical significance outside measurement contexts. However, as Healey notes,19 this solution is unsatisfying not only from a hardcore realist but even from a more pragmatically-oriented point of view in that ascribing a probability to a NQMC can in some cases be legitimate with respect to situations where no measurements are performed at all. As an example of a situation where this is the case, consider a double-slit experimental setup, where electrons passing through a double-slit are coupled to a heat bath of scattering photons. In this case, different from that of electrons not coupled to photons, no wave-type interference pattern can be observed on a screen behind the double-slit and the probabilities for electrons on the screen can be computed from their probabilities passing through the individual slits. In that sense, one can treat the NQMCs “The electron is in the volume interval
, and to deny that quantum theory has any empirical significance outside measurement contexts. However, as Healey notes,19 this solution is unsatisfying not only from a hardcore realist but even from a more pragmatically-oriented point of view in that ascribing a probability to a NQMC can in some cases be legitimate with respect to situations where no measurements are performed at all. As an example of a situation where this is the case, consider a double-slit experimental setup, where electrons passing through a double-slit are coupled to a heat bath of scattering photons. In this case, different from that of electrons not coupled to photons, no wave-type interference pattern can be observed on a screen behind the double-slit and the probabilities for electrons on the screen can be computed from their probabilities passing through the individual slits. In that sense, one can treat the NQMCs “The electron is in the volume interval
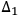 ” (implicating that it passes through the first slit) and “The electron is in the volume interval
” (implicating that it passes through the first slit) and “The electron is in the volume interval
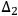 ” (implicating that it passes through the second) as having determinate truth values for each electron. One can thus consistently interpret the Born Rule as ascribing probabilities to these NQMCs even if it is not experimentally determined for the electron through which slit it actually passes.
” (implicating that it passes through the second) as having determinate truth values for each electron. One can thus consistently interpret the Born Rule as ascribing probabilities to these NQMCs even if it is not experimentally determined for the electron through which slit it actually passes.
Generalising this observation, Healey proposes that quantum theory “license[s] claims about the real value only of a dynamical variable represented by an operator that is diagonal in a preferred basis” (Healey forthcoming, forthcoming, 16). His proposal, in effect, is that ascribing a probability to an NQMC involving reference to an observable
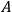 is legitimate for an agent whenever the density operator
is legitimate for an agent whenever the density operator
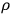 she assigns to the system is diagonal in a preferred Hilbert space basis, typically selected by environment-induced decoherence. In that case the reduced density operator assigned to the system by agents taking into account its coupling to the environment and performing the trace over the environmental degrees of freedom becomes (at least approximately) diagonal in an environment-selected basis.20 As in the special case of the double-slit setup with photons mentioned before, it is unproblematic in these contexts to assume that NQMCs about observables having this basis in their spectral decomposition have determinate truth values. It is therefore natural for the Rule Perspective to hold that the Born Rule defines probabilities just for those NQMCs which refer to observables whose spectral decomposition makes the density matrix assigned by an agent uniquely diagonal. Arguably, the Rule Perspective should say that these NQMCs are what quantum probabilities are probabilities of.
she assigns to the system is diagonal in a preferred Hilbert space basis, typically selected by environment-induced decoherence. In that case the reduced density operator assigned to the system by agents taking into account its coupling to the environment and performing the trace over the environmental degrees of freedom becomes (at least approximately) diagonal in an environment-selected basis.20 As in the special case of the double-slit setup with photons mentioned before, it is unproblematic in these contexts to assume that NQMCs about observables having this basis in their spectral decomposition have determinate truth values. It is therefore natural for the Rule Perspective to hold that the Born Rule defines probabilities just for those NQMCs which refer to observables whose spectral decomposition makes the density matrix assigned by an agent uniquely diagonal. Arguably, the Rule Perspective should say that these NQMCs are what quantum probabilities are probabilities of.
According to this line of thought, whether an agent is entitled to treat an NQMC as having a determinate truth value depends on the state she assigns to the system and, therefore, on her epistemic situation. In contrast to this agent dependence, however, as Healey notes, “the content of an NQMC about a system
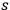 does not depend on agent situation ... [in that] ... it is independent of the physical as well as the epistemic state of any agent (human, conscious, or neither) that may make or evaluate it” (Healey forthcoming, forthcoming, 25). Thus, while quantum theory itself is non-descriptive according to the Rule Perspective insofar as quantum states are not regarded as descriptions of physical states of affairs, it nevertheless functions as a way of organizing descriptive claims. It does so, first, by giving a criterion of under which conditions these claims can be treated as having determinate truth values and, second, by providing a method of computing probabilities for these claims to be true. In particular, it licenses NQMCs about macroscopic (pointer) observables for which the density matrices we assign to them when we take into account decoherence effects are typically (at least approximately) diagonal. If we want to use the quantum mechanical formalism correctly, we therefore have to treat statements about measurement devices as having determinate truth values and in that sense must assume that measurements do have outcomes. This line of thought may dispel the felt need of accounting for determinate measurement outcomes in terms of a dynamical explanation and in that sense completes the dissolution of the measurement problem.
does not depend on agent situation ... [in that] ... it is independent of the physical as well as the epistemic state of any agent (human, conscious, or neither) that may make or evaluate it” (Healey forthcoming, forthcoming, 25). Thus, while quantum theory itself is non-descriptive according to the Rule Perspective insofar as quantum states are not regarded as descriptions of physical states of affairs, it nevertheless functions as a way of organizing descriptive claims. It does so, first, by giving a criterion of under which conditions these claims can be treated as having determinate truth values and, second, by providing a method of computing probabilities for these claims to be true. In particular, it licenses NQMCs about macroscopic (pointer) observables for which the density matrices we assign to them when we take into account decoherence effects are typically (at least approximately) diagonal. If we want to use the quantum mechanical formalism correctly, we therefore have to treat statements about measurement devices as having determinate truth values and in that sense must assume that measurements do have outcomes. This line of thought may dispel the felt need of accounting for determinate measurement outcomes in terms of a dynamical explanation and in that sense completes the dissolution of the measurement problem.
6 Reality Presupposed
In the previous section quantum theory was characterized from the point of view of the Rule Perspective as a method of organizing descriptive “non-quantum” claims and attributing probabilities to them. This makes it clear that the Rule Perspective, far from denying that objective descriptions of physical states of affairs can be given, is based on the presupposition that objective descriptions exist in the form of NQMCs. The potential accusation against the Rule Perspective that it supposedly relies on an implausible and unattractive anti-realism or instrumentalism completely misses the mark: The Rule Perspective, as we see, cannot even coherently be formulated without making the realist assumption that physical states of affairs exist and that they can be described in terms of NQMCs.
If at all, the Rule Perspective is non-realist in the sense that it reads the most genuinely quantum conceptual resource—quantum states—as non-descriptive. As I have argued in Friederich 2011, however, this does not exclude an interpretation of the “structure and internal functioning” Timpson 2008, 582 of the quantum theoretical formalism as a whole to reflect objective features of physical reality itself. Furthermore, quantum theory as a method of organizing descriptive claims in the sense discussed in the previous section can still be seen as having been discovered rather than freely created or invented by the human mind 21 Conceiving of quantum states as tools of organizing descriptive claims depending on one's epistemic situation rather than as descriptions of physical states of affairs themselves does not mean to deny that physical states of affairs do exist. It just means that the conceptual resources needed to describe them must be non-quantum.
References
Bub, J. (2007). Quantum probabilities as degrees of belief. Studies in History and Philosophy of Modern Physics 38: 232-254
Caves, C. M., C. A. Fuchs, C.A. F. (2002a). Quantum probabilities as Bayesian probabilities. Physical Review A 65: 022305
- (2002b). Unknown quantum states: The quantum de Finetti representation. Journal of Mathematical Physics 44: 4537-4559
- (2007). Subjective probability and quantum certainty. Studies in History and Philosophy of Modern Physics 38: 255-274
Fleming, G. N. (1988). Lorentz invariant state reduction, and localization. In: PSA 1988, Vol. 2 Ed. by A. Fine, M. Forbes. 112-126
Friederich, S. (2011). How to spell out the epistemic conception of quantum states. Studies in History and Philosophy of Modern Physics 42: 149-157
Fuchs, C. A. (2002). Quantum mechanics as quantum information (and only a little more). In: Quantum Theory: Reconsideration of Foundations Ed. by A. Khrennikov. 463-543
- (2010). QBism, the perimeter of quantum Bayesianism.
Fuchs, C. A., A. Peres (2000). Quantum theory needs no `interpretation'. Physics Today 53: 70-71
Harrigan, N., R. W. Spekkens (2010). Einstein, incompleteness, and the epistemic view of quantum states. Foundations of Physics 40: 125-157
Healey, R. (forthcoming). Quantum theory: a pragmatist approach. British Journal for the Philosophy of Science
Heisenberg, W. (1958). Physics and Philosophy: The Revolution in Modern Science..
Marchildon, L. (2004). Why should we interpret quantum mechanics?. Foundations of Physics 34: 1453-1466
Maudlin, T. (2011). Quantum Theory and Relativity Theory: Metaphysical Intimations of Modern Physics..
Mermin, N. D. (2003). Copenhagen computation. Studies in History and Philosophy of Modern Physics 34: 511-522
Myrvold, W. C. (2002). On peaceful coexistence: is the collapse postulate incompatible with relativity?. Studies in History and Philosophy of Modern Physics 33: 435-466
Pitowsky, I. (2003). Betting on the outcomes of measurements: A Bayesian theory of quantum probability?. Studies in History and Philosophy of Modern Physics 34: 395-414
Ruetsche, L. (2002). Interpreting quantum theories. In: The Blackwell Guide to the Philosophy of Science Ed. by P. Machamer, M. Silberstein. 199-226
Schack, R. (2003). Quantum theory from four of Hardy's axioms. Foundations of Physics 33: 1461-1468
Schlosshauer, M. (2005). Decoherence, the measurement problem, and interpretations of quantum mechanics. Reviews of Modern Physics 76: 1267-1305
Searle, J. (1969). Speech Acts..
Spekkens, R. W. (2007). Evidence for the epistemic view of quantum states: A toy theory. Physical Review A 75: 032110
Timpson, C. G. (2008). Quantum Bayesianism: A study. Studies in History and Philosophy of Modern Physics 39: 579-609
Zbinden, H. (2001). Experimental test of nonlocal quantum correlations in relativistic configurations. Physical Review A 63: 022111
Footnotes
For studies defending versions of the epistemic conception of states and views in a similar spirit, see (Fuchs and Peres 2000; Mermin 2003; Mermin 2003; Fuchs 2002; Pitowsky 2003; Schack 2003; Bub 2007; Caves et.al. 2007; Spekkens 2007; Fuchs 2010; Healey forthcoming, forthcoming: Friederich 2011).
See (Spekkens 2007; Harrigan and Spekkens 2010) for illuminating discussions of accounts of this type, both from a systematic and from a historical perspective.
See Fuchs and Peres 2000.
At least if one assumes, as usual, the so-called eigenstate-eigenvalue link which says that for a system in a state
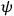 an observable A has a definite value a if and only if it is an eigenstate of the operator corresponding to A with eigenvalue a.
an observable A has a definite value a if and only if it is an eigenstate of the operator corresponding to A with eigenvalue a.
See, for instance, Ruetsche 2002, 209 for a lucid account of these two criticisms.
See Maudlin 2011, ch. 7 for a very useful and up-to-date exposition of this difficulty.
See Zbinden 2001 for a discussion of experiments carried out in such a setup.
See Fleming 1988 for a hyperplane-dependent formulation of state reduction and Myrvold 2002 for a defense of that approach. For criticism, see Maudlin 2011, ch. 7, which comes to a rather general negative verdict as to whether relativity theory and standard quantum theory can be consistently combined at all, based, however, on the presupposition that the ontic conception of quantum states is correct.
See Fuchs 2002, fn. 9 and sec. 7, in particular. See also Timpson 2008, sec. 2.3.
This is how Fuchs describes it, see Fuchs 2002, 7.
See Caves et.al. 2002b.
See Friederich 2011, sec. 4 and 5, for the slightly more detailed original version of the considerations presented in this section.
Phrases within quotation marks in this and the following paragraphs are all taken from the passage from Searle 1969 just cited.
See (Healey forthcoming, forthcoming, sec. 2), for a more detailed investigation of in which sense quantum probabilities can be regarded as objective and agent-dependent at the same time.
See (Fuchs 2002, 7; Schack 2003; Fuchs 2010, 18).
It seems likely that this observation can be used to answer a criticism brought forward against quantum Bayesianism by Timpson. According to this criticism, a quantum Bayesian is committed to the systematic endorsement of pragmatically paradoxical sentences of the form “I am certain that p (e. g., that the outcome will be spin-up in the
 -direction) but it is not certain that p” Timpson 2008, 604, for instance when assigning a pure state, which necessarily ascribes probability
-direction) but it is not certain that p” Timpson 2008, 604, for instance when assigning a pure state, which necessarily ascribes probability
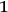 to at least one possible value of an observable. Timpson offers the first half of this sentence (“I am certain that p”) as a quantum Bayesian translation of a state assignment (“I assign
to at least one possible value of an observable. Timpson offers the first half of this sentence (“I am certain that p”) as a quantum Bayesian translation of a state assignment (“I assign
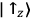 ”), but the quantum Bayesian might reject this translation by claiming that the Born Rule probabilities derived from the state she assigns are not measures of her actual degrees of belief but rather prescriptions for what degrees of belief she should have, given certain presuppositions.
”), but the quantum Bayesian might reject this translation by claiming that the Born Rule probabilities derived from the state she assigns are not measures of her actual degrees of belief but rather prescriptions for what degrees of belief she should have, given certain presuppositions.
See, for instance, Heisenberg 1958, 30.
See (Healey forthcoming, forthcoming, sec. 3). The reasoning given in the text is strongly based on the discussion of recent diffraction experiments presented there in great detail.
See Schlosshauer 2005 for a helpful introduction to decoherence and clarification of its relevance for foundational issues.
See Friederich 2011, sec. 6 for more detailed considerations on this option.
