Abstract. Different observers do not have to agree on how they identify a quantum system. We explore a condition based on algorithmic complexity that allows a system to be described as an objective “element of reality.” We also suggest an experimental test of the hypothesis that any system, even much smaller than a human being, can be a quantum mechanical observer.
1 Introduction
Quantum mechanical formalism has an orthodox interpretation that relies on the cut between the observer and the system observed Dirac 1930 von Neumann 1932. This “shifty split” Bell 1990 of the world into two parts cannot be removed: the formalism only applies if the observer and the system are demarcated as two separate entities. Physical properties of the system, on one side of the split, do not exist independently of the observer, on the other side of the split, and can only be instantiated during the observation, or `measurement,' of some dynamical variable of the system chosen by the observer.
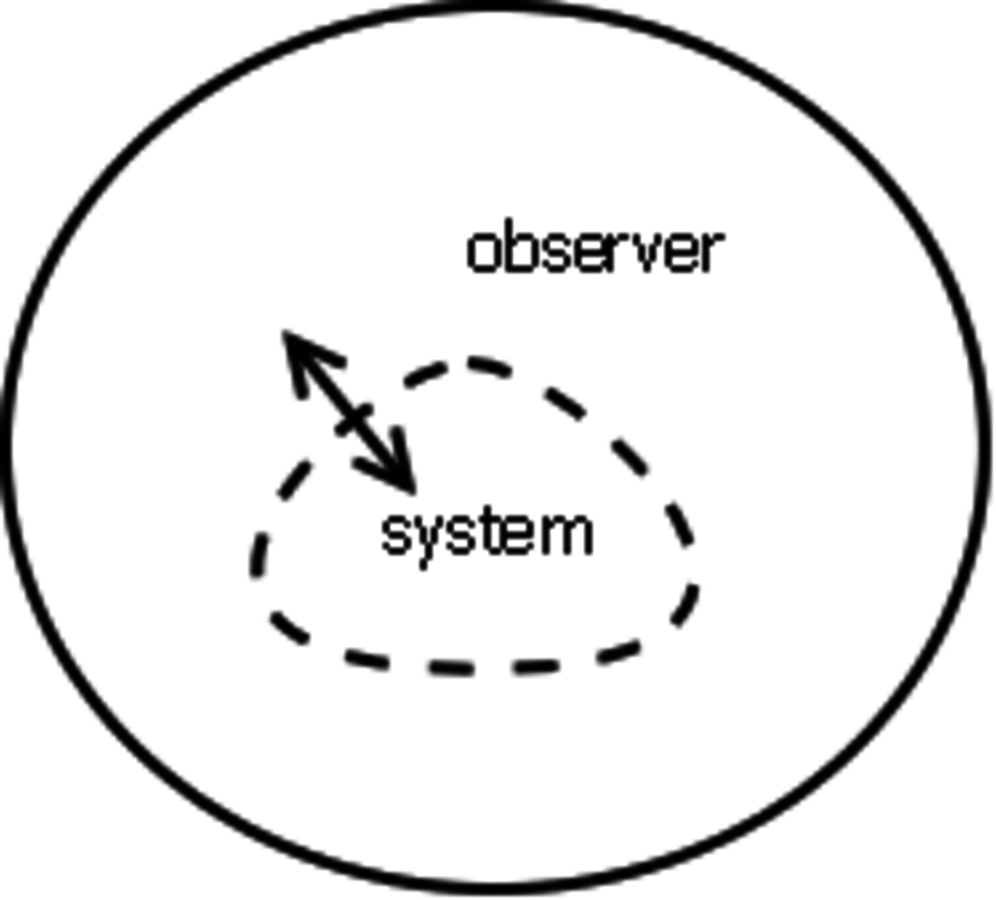
Fig. 1: A “shifty split” between the observer and the quantum system.
The observer is essential for quantum mechanics, but precisely to whom or to what thing does this word refer? There is no consensus. What is extraordinarily difficult, Wheeler 1983 emphasized, is to state sharply and clearly where “the community of observer-participators” begins and where it ends. Quantum mechanics itself says nothing about the physical composition of the observer: whatever is meant by the word has no quantum mechanical description and lies outside physical theory. One cannot infer from a set of quantum mechanical measurements if the observer is a human being, a machine, a stone, a Martian, or the whole Universe.
It is remarkable that although nothing can be said about who the observer is, quantum mechanics gives unequivocal prescriptions for the content of the observer's observation. Differently constituted observers, even if one is a butterfly on Earth and the other a drop of methane on Titan, will obtain the same probabilistic results provided that they manage to measure the same quantum system. How is this possible? Only because the mathematics of quantum mechanics is abstract: it deals with `systems' and `observers,' not with methane or butterflies.
The question of the observer's exact physical constituency is not dealt with from within quantum mechanics; it is left for philosophy. Different interpretations of quantum mechanics provide different answers. Some say that only conscious human beings can be observers; others state that anything qualifies, even a single electron. Each answer to the question `what is an observer' comes with a corresponding answer to the question `can observers disagree' or `what makes them agree.'
As a part of his relative-state interpretation, Everett argued that observers
are physical systems with memory, i.e., “parts... whose states are in
correspondence with past experience of the observers” Everett 1957. We
call this a universal observer hypothesis: any system with certain
information-theoretic properties can serve as quantum mechanical observer,
independently of its physical constituency, size, presence or absence of
conscious awareness and so forth. In this vein, Rovelli claimed that observers
are merely systems whose degrees of freedom are correlated with some property
of the observed system: “Any system can play the role of observed system and
the role of observing system. [ ...] The fact that observer
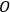 has
information about system
has
information about system
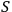 (has measured
(has measured
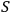 ) is expressed by the existence
of a correlation [ ...]” Rovelli 1996. However, the universal observer hypothesis has remained a controversial statement to this day. For example, Peres claims in the way exactly opposite to Rovelli's, that “the two electrons in the ground state of the helium atom are correlated, but no one would say that each electron `measures' its partner” Peres 1986. Our purpose is to clarify an information-theoretic definition of quantum mechanical observer and to propose a physical test of this hypothesis.
) is expressed by the existence
of a correlation [ ...]” Rovelli 1996. However, the universal observer hypothesis has remained a controversial statement to this day. For example, Peres claims in the way exactly opposite to Rovelli's, that “the two electrons in the ground state of the helium atom are correlated, but no one would say that each electron `measures' its partner” Peres 1986. Our purpose is to clarify an information-theoretic definition of quantum mechanical observer and to propose a physical test of this hypothesis.
We start by a historical review in Section 2. In Section 3 we give a general definition of observer based on the intuitive feeling that a key component of observation is system identification. Then we apply to it the notion of Kolmogorov complexity, which is the main tool of ensuing analysis. In Section 4 this approach is developed to germinate a definition of quantum and classical systems. In Section 5 we consider a family of observers and require that a system be identified by them in the same way, thereby giving an information-theoretic criterion of an “element of reality.” In Section 6 we show that observers can be allowed some disagreement while still maintaining an unambiguous identification of the observed element of reality. Finally, in Section 7 we suggest an experimental test of the universal observer hypothesis.
2 Observer as a Problem
2.1 Observer in the Copenhagen Orthodoxy
Bohr's lecture at Como in 1927 became the foundation of what later came to be known as the Copenhagen interpretation of quantum mechanics. Despite being a universal and orthodox reference in the debate on quantum mechanics, the Copenhagen interpretation has a variety of formulations none of which is the accepted dogma Peres 1986. Its main point can be described by the following quote from Bohr: “Only with the help of classical ideas is it possible to ascribe an unambiguous meaning to the results of observation. [ ...] It lies in the nature of physical observation, that all experience must ultimately be expressed in terms of classical concepts.” Bohr 1934, 94 Two different readings of Bohr's statement exist, related to what exactly is meant by “classical.” The first is a straightforward inference that quantum mechanics requires classical mechanics:
It is in principle impossible to formulate the basic concepts of quantum mechanics without using classical mechanics. Landau and Lifshitz 1977, 2
On the second reading, one maintains that quantum mechanical experiments can only be described by the classical language, which in turn leads us to classical mechanics, but it is the language that is a crucial ingredient:
Bohr went on to say that the terms of discussion of the experimental conditions and of the experimental results are necessarily those of `everyday language,' suitably `refined' where necessary, so as to take the form of classical dynamics. It was apparently Bohr's belief that this was the only possible language for the unambiguous communication of the results of an experiment. Bohm 1971, 38
The choice between classical mechanics and classical language is not always visible and many authors have failed to distinguish between the two formulations. A direct reference to classical mechanics means, for those who support this view, that the world consists of mechanical systems only, whether quantum or classical, and no external observer is necessary. On the contrary, an invocation of the classical language, concepts, or terms—and Bohr himself has always used these words—implies that the formulation of the problem includes somebody who is in command of classical concepts: the experimenter. This experimenter prepares the quantum system and then measures it acting as a quantum mechanical observer. Then observers possess a linguistic faculty because, according to Bohr's dictum, they need to communicate between themselves unambiguously.
The mechanistic point of view and the linguistic point of view differ in the ways they account for the problem of agreement. Mechanistically, one assumes that the properties of classical systems exist objectively, i.e. independently of bringing other systems into consideration. Objectivity then guarantees that any further classical mechanical system will be able to interact with the initial system and acquire the same property, which encodes the measurement result. Mechanistic observers agree because disagreement is not classically observed.
The answer is less straightforward from the linguistic point of view. Observers agree on the results of quantum measurements because they agree on the use of classical concepts. But why do they agree on linguistic usage? How do they establish their agreement? How does it come about? It is a matter of pure convention usually left unanalyzed by the Copenhagen interpretation.
2.2 London and Bauer
John von Neumann's magisterial book on quantum mechanics first appeared in German in 1932 von Neumann 1932. It offered a theory of measurement that were to become a standard not only for the Copenhagen interpretation but for quantum mechanics as a physical theory in general. However, von Neumann's musings about the place of the observer were not entirely clear and satisfactory. The formalism worked perfectly, but what was exactly its meaning?
Writing as early as 1939, London and Bauer set the tone of one of the main branches of the post-von Neumann debate on the interpretation of quantum mechanics. They remark that quantum mechanics cannot ascribe properties to the quantum system in itself, only if there is a link to an observer. This observer is for London and Bauer a human person. An objective description of reality is therefore impossible and “it seems that the result of measurement is intimately linked to the consciousness of the person making it” London and Bauer 1939, 48.1 Von Neumann's cut between the observer and the observed system is here pushed to the extreme position, leaving all physical systems on one side, including light photons, the eye and the nerves, and only leaving the observer's `organ' of awareness, namely consciousness, on the other.
If this were true, why would objectivity be possible at all and why have physicists not yet become solipsists? Why do two physicists agree on what constitutes the object of their observation and on its properties? Because, according to London and Bauer 1939, 49, there exists something like a “community of scientific consciousness, an agreement on what constitutes the object of the investigation.” The nature of this scientific consciousness remains however mysterious. London and Bauer only conclude that “it must yet be looked into.”
2.3 Wigner
Remarks by London and Bauer were further developed by Eugene Wigner 1961. Consciousness of the observer “enters the theory unavoidably and unalterably” and corresponds to the impression produced by the measured system on the observer. Answering the question of realism, Wigner notes that the wave function “exists” only in the sense that “the information given by the wave function is communicable.” Observers agree because they communicate measurement results to one another:
The communicability of information means that if someone else looks at timeand tells us whether he saw a flash, we can look at time
and observe a flash with the same probabilities as if we had seen or not seen the flash at time
ourselves.
The first observer tells us the result of his measurement: communication for Wigner is linguistic. The second observer, in this example of Wigner's, puts himself in the position of the first observer and acts just like him. This is only possible because the second observer has been told the measurement result by the first one.
Do observers actually have to communicate or is it enough to require that they simply could communicate the information about the measurement? Here Wigner's position is vague. On the one hand, he states, “If someone else somehow determines the wave function of a system, he can tell me about it [ ...],” which requires a mere possibility of communication but no sending of actual information. On the other hand, Wigner famously analyzes the following situation labeled `Wigner's friend':
It is natural to inquire about the situation if one does not make the observation oneself but lets someone else carry it out. What is the wave function if my friend looked at the place where the flash might show at time? The answer is that the information available about the object cannot be described by a wave function. One could attribute a wave function to the joint system: friend plus object, and this joint system would have a wave function also after the interaction, that is, after my friend has looked. I can then enter into interaction with this joint system by asking my friend whether he saw a flash. [ ...] The typical change in the wave function occurred only when some information (the yes or no of my friend) entered my consciousness.
Although he calls this situation natural, Wigner is the only one among the founding fathers of quantum theory to have addressed it explicitly. Here Wigner's agreement with his friend is clearly possible thanks to the linguistic communication between them, but this communication itself is not a quantum measurement: whatever the situation, Wigner always knows the question he should put to his friend and fully trusts the answer, always yes or no. Communication from the friend must actually occur before the wave function could be known by Wigner; it is not enough that this communication be merely possible. As with the linguistic reading of the Copenhagen interpretation, Winger's interpretation involving consciousness of the observer leaves open the exact mechanism, whether a human convention or a physical given, of the agreement between observers.
Wigner also touches on the question of belief and trust in his discussion of the repeatability of experiments in physics. To explore the statistical nature of the predictions of quantum mechanics, it is necessary to be able to produce many quantum systems in the same state; subsequently these systems will be measured. One can never be absolutely sure, Wigner stipulates, that one has produced the same state of the system. We usually “believe that this is the case” and we are “fully convinced of all this” Wigner 1976, 267, even if we have not tried to establish experimentally the validity of the repeated preparation of the same state. What is at work here is again a convention shared by all physicists. How do they know that repeated preparations produce the same state if they do not measure each and every specimen in order to verify it? The answer is that they have common experience and a convention on what a `controlled experiment' amounts to, and their respect of this commonly shared and empirically validated rules enables them to postulate the existence of repeated states even in the situations which had never been tested before. This is how physical theory with its laws and a precise methodology arises by way of abstraction (`elevation,' as Einstein or Poincaré would say Friedman 2001, 88) from the physicist's empirical findings and the heuristics of his work.
2.4 Everett
What is important about the observer? Only his function of an informational agent, not his physical constituency. The need to refer to consciousness exists, insofar as only consciousness can distinguish a mere physical correlation, e.g. of an external system with the observer's eye, from the information actually available to the observer, i.e. such that he can act upon in the future. Other characteristics are irrelevant: say, the observer's age plays no role (“there is little chance of making a big mistake if one does not know [the observer's] age” London and Bauer 1939, 43).
Treating the observer as an informational agent requires that we say precisely what makes different systems possessing information into observers. In other words, what is the nature of a convention shared by all observers, whose workings we notice when apparently unrelated measurements by different observers come out in a consistent way? Brillouin believes that information must be defined with the exclusion of all human element George 1953, 360, in which case the convention between observers must necessarily have a physical, as opposed to linguistic or cultural, origin. Watanabe finds such a physical origin in the direction of time shared by all observers: “The past-to-future directions of all observers coincide. This statement has a well-defined physical meaning, for `positive time direction' is a Lorentz-invariant concept” George 1953, 387. But both Brillouin's and Watanabe's ideas proved to be sterile in the history of physics. Time-directedness, for once, may be a necessary requirement, because, as we shall see later, observers are thermodynamical systems. But it is far from clear if Watanabe's shared time direction is a sufficient or even a necessary condition.
Hugh Everett 1957 thought differently. Observers are for him systems that can be described in purely physical terms. These systems possess memory, defined as “parts [ ...] whose states are in correspondence with past experience of the observers.” Observers do not have to be human: they could be “automatically functioning machines, possessing sensory apparatus and coupled to recording devices.” Memory records are thus fundamental: it is memory that makes any physical system an observer. Everett continues, “if we are to be able to call the interaction an observation at all, the requirement that the observer's state change in a manner which is different for each eigenfunction is necessary.” Repeatability relies on the necessary assumption that the eigenstates of the system be unchanged during measurement.
Everett was the first to explicitly consider the problem of several observers. The “interrelationship between several observers” is an act of communication between them, which Everett treats as establishing a correlation between their memory configurations. The consequences are described with remarkable clarity:
1When several observers have separately observed the same quantity in the object system and then communicated the results to one another they find that they are in agreement. This agreement persists even when an observer performs his observation after the result has been communicated to him by another observer who has performed the observation.
2Let one observer perform an observation of a quantity
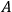 in the object system, then let a second perform an observation of a quantity
in the object system, then let a second perform an observation of a quantity
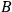 in this object system which does not commute with
in this object system which does not commute with
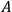 , and finally let the first observer repeat his observation of
, and finally let the first observer repeat his observation of
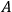 . Then the memory system of the first observer will not in general show the same result for both observations. [ ...]
. Then the memory system of the first observer will not in general show the same result for both observations. [ ...]
3Consider the case when the states of two object systems are correlated, but where the two systems do not interact. Let one observer perform a specified observation on the first system, then let another observer perform an observation on the second system, and finally let the first observer repeat his observation. Then it is found that the first observer always gets the same result both times, and the observation by the second observer has no effect whatsoever on the outcome of the first's observations.
2.5 Rovelli
Rovelli 1996 proposed a relational interpretation of quantum mechanics. All physical systems have the capacity to act as observers, i.e., possess information about other physical systems. Information should be seen as an observer-dependent, rather than objective, notion. It is information in Shannon's sense indexed by two parameters: the first related to the observed system about which this information has been obtained, the second related to the observing system that has obtained information about the first system. Trying to remove the second index and to 'liberate' the notion of information from its relational sense is both impossible and meaningless. Objective information independent of the observing system does not exist.
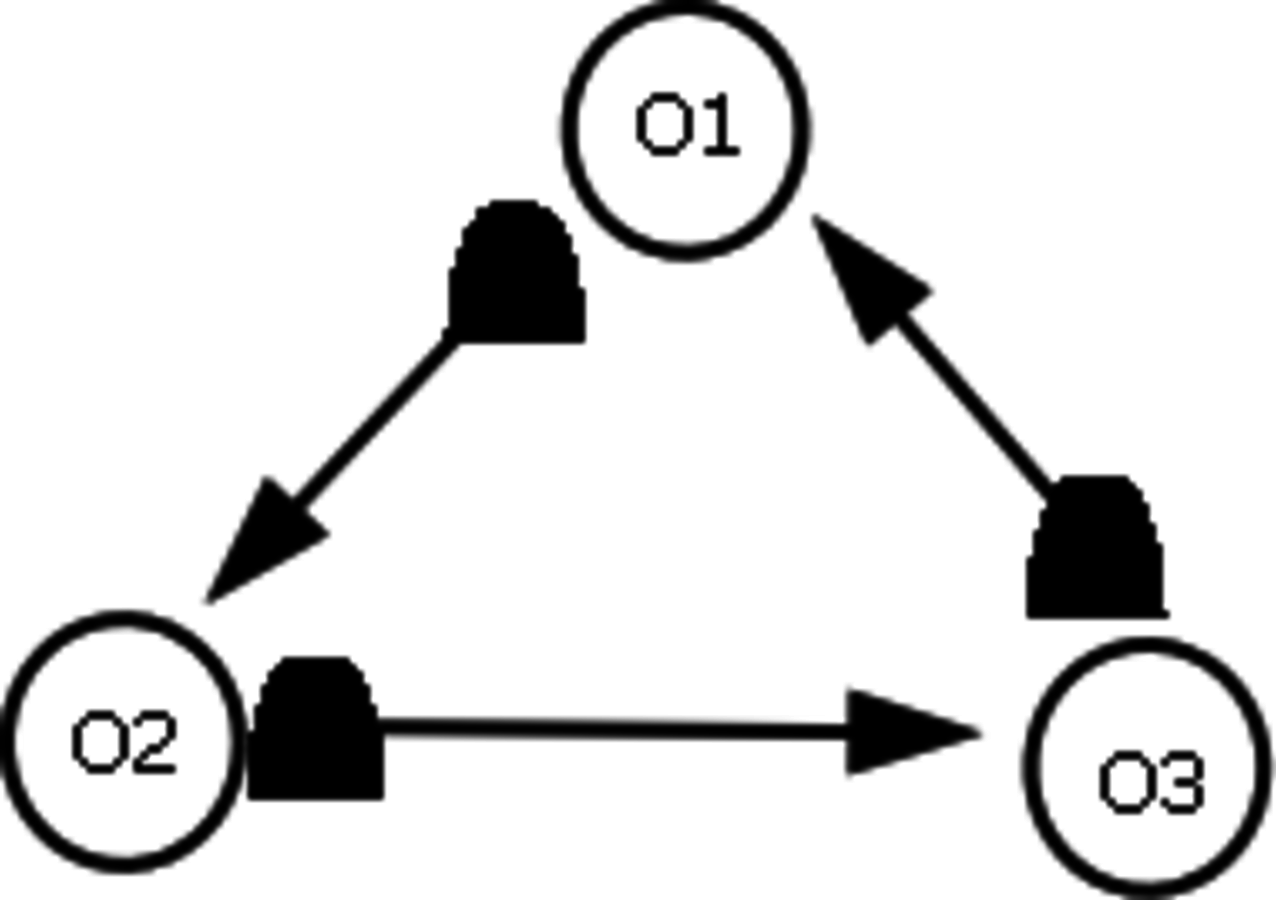
However, the question of intersubjective agreement remains unclear. If each observer acts on his own and information is always defined relative to some observer, why do different observers agree on the measurement result and attribute the same state to the quantum system? For Rovelli, the answer lies in the interaction between observers, which is a quantum mechanical process like any other and, consequently, must be described in the same language of relative information. This information is encoded in the correlations between physical degrees of freedom of the observers. Now imagine three observers in a triangle (see Figure 2), with
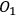 observing
observing
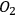 ,
,
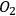 observing
observing
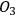 , and
, and
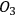 observing
observing
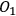 .
.
Some of the degrees of freedom of
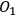 are correlated with some degrees of freedom of
are correlated with some degrees of freedom of
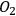 . Similarly, some degrees of freedom of
. Similarly, some degrees of freedom of
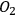 are correlated with the degrees of freedom of
are correlated with the degrees of freedom of
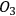 , and the degrees of freedom of
, and the degrees of freedom of
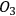 are correlated with those of
are correlated with those of
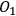 . These correlations must be self-consistent, i.e., no paradox must emerge from the circular correlation. How is this requirement realized physically? Perhaps it is always the case that when an observer is observed by another system, the degrees of freedom that the other system can `see' are never the same as the degrees of freedom in which the observer encodes his own measurement data. Or perhaps some other mechanism is at work, which precludes us from running into a contradiction. This issue is not explored by Rovelli and remains an open question.
. These correlations must be self-consistent, i.e., no paradox must emerge from the circular correlation. How is this requirement realized physically? Perhaps it is always the case that when an observer is observed by another system, the degrees of freedom that the other system can `see' are never the same as the degrees of freedom in which the observer encodes his own measurement data. Or perhaps some other mechanism is at work, which precludes us from running into a contradiction. This issue is not explored by Rovelli and remains an open question.
3 Observer as a System Identification Algorithm
What characterizes an observer is that it (or he or she) has information about some physical system. This information fully or partially describes the state of the system. The observer then measures the system, obtains further information and updates his description accordingly. The physical processes of measuring the system, updating the information and ascribing a state to the system may happen in many different ways depending on the physical constitution of the observer. The memory of a computer acting as an observer, for instance, is not the same as human memory, and measurement devices vary in their design and functioning. Still one feature unites all observers: whatever they do, they do it to a system. In quantum mechanics, defining an observer goes hand in hand with defining a system under observation. An observer without a system is a meaningless nametag, a system without an observer who measures it is a mathematical abstraction. What remains constant throughout measurement is the identification, by the observer, of the quantum system.
Quantum systems aren't like sweets: they don't melt. Take a general thermodynamic system interacting with other systems. Such a system can dissipate, diffuse, or dissolve, and thus stop being a system. If at first a cube of ice gurgling into tepid water is definitely a thermodynamic system, it makes no sense to speak about it being a system after it has dissolved. Quantum systems are not like this. Their states may evolve, but the observer knows how to tell the system he observes from the rest or the environment. An electron in a certain spin state remains an electron after measurement, i.e., it remains a system with a particular set of degrees of freedom. The observer maintains the identity of the system notwithstanding a change in the state of this system that may or may not occur. So, whatever else he might happen to be, the observer is primarily a system identification machine. Different observers having different features (clock hands, eyes, optical memory devices, internal cavities, etc.) all share this central characteristic.
Definition 5.1: An observer is a system identification algorithm (SIA).
Particular observers can be made of flesh or, perhaps, of silicon. `Hardware' and `low-level programming' are different for such observers, yet they all perform the task of system identification. This task can be defined as an algorithm on a universal computer, e.g. the Turing machine: take a tape containing the list of all degrees of freedom, send a Turing machine along this tape so that it puts a mark against the degrees of freedom that belong to the quantum system under consideration. Any concrete SIA may proceed in a very different manner, yet all can be modelled with the help of this abstract construction.
The SIAs whose physical realization may differ share one property that does not depend on the hardware: their algorithmic, or Kolmogorov, complexity. Any SIA can be reconstructed from a binary string of some minimal length (which is a function of this SIA) by a universal machine. As shown by Kolmogorov 1965, this minimal compression length defines the amount of information in the SIA and does not depend (up to a constant) on the realization of the SIA on this or that hardware. The common-lore view of a multitude of individual observers, one hastily printing, another yawning, a third one moving around his DNA strands, should in our opinion be superseded by a view of different SIAs, each with its algorithmic complexity defined via a universal machine.
4 Quantum and Classical Systems
Each quantum system has a certain number of degrees of freedom, which we think about as being independent parameters needed in order to characterize the state of the system. For example, a system with only two states (spin-up and spin-down) has one degree of freedom and can be described by one parameter
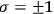 . If we write down these parameters as a binary string, the Kolmogorov complexity of that string is at least the number of the degrees of freedom of the system, i. e.,
. If we write down these parameters as a binary string, the Kolmogorov complexity of that string is at least the number of the degrees of freedom of the system, i. e.,
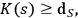
|
1 |
where
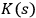 is the Kolmogorov complexity of the binary string
is the Kolmogorov complexity of the binary string
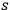 representing the parameters of the system
representing the parameters of the system
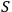 , and
, and
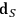 is the number of the degrees of freedom in
is the number of the degrees of freedom in
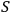 . In what follows the notation
. In what follows the notation
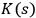 and
and
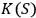 will be used interchangeably.
will be used interchangeably.
When we say that an observer
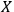 observes a quantum system
observes a quantum system
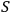 , it is usually the case that
, it is usually the case that
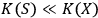 . In this case the observer will have no trouble keeping track of all the degrees of freedom of the system; in other words, the system will not `dissolve' or `melt' in the course of dynamics. However, it is also possible that
. In this case the observer will have no trouble keeping track of all the degrees of freedom of the system; in other words, the system will not `dissolve' or `melt' in the course of dynamics. However, it is also possible that
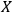 identifies a system with
identifies a system with
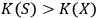 . For such an observer, the identity of system
. For such an observer, the identity of system
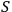 cannot be maintained and some degrees of freedom will fall out from the description that
cannot be maintained and some degrees of freedom will fall out from the description that
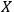 makes of
makes of
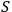 .
.
Definition 6.1:
System
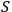 is called quantum with respect to observer
is called quantum with respect to observer
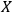 if
if
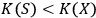 , meaning that
, meaning that
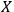 will be able to maintain a complete list of all its degrees of freedom. Otherwise
will be able to maintain a complete list of all its degrees of freedom. Otherwise
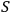 is called classical with respect to
is called classical with respect to
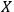 .
.
Suppose that
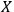 observes a quantum system
observes a quantum system
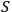 and another observer
and another observer
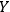 observes both
observes both
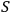 and
and
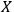 . If
. If
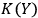 is greater than both
is greater than both
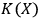 and
and
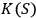 , observer
, observer
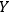 will identify both systems as quantum systems. In this case
will identify both systems as quantum systems. In this case
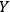 will typically treat the interaction between
will typically treat the interaction between
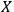 and
and
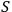 as an interaction between two quantum systems. If, however,
as an interaction between two quantum systems. If, however,
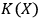 and
and
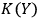 are close,
are close,
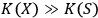 and
and
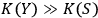 but
but
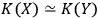 , then
, then
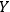 will see
will see
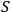 as a quantum system but the other observer,
as a quantum system but the other observer,
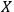 , as a classical system. An interaction with a classical system, which we usually call `observation,' is a process of decoherence that occurs when the Kolmogorov complexity of at least one of the systems involved approaches the Kolmogorov complexity of the external observer. In this case
, as a classical system. An interaction with a classical system, which we usually call `observation,' is a process of decoherence that occurs when the Kolmogorov complexity of at least one of the systems involved approaches the Kolmogorov complexity of the external observer. In this case
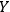 cannot maintain a complete description of
cannot maintain a complete description of
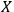 interacting with
interacting with
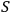 and must discard some of the degrees of freedom. If we assume that all human observers acting in their SIA capacity have approximately the same Kolmogorov complexity, this situation may provide an explanation of the fact that we never see a human observer (or, say, a cat) as a quantum system.
and must discard some of the degrees of freedom. If we assume that all human observers acting in their SIA capacity have approximately the same Kolmogorov complexity, this situation may provide an explanation of the fact that we never see a human observer (or, say, a cat) as a quantum system.
One welcome consequence of Definitions 5.1 and 6.1 is that Kolmogorov complexity
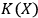 is not computable. We as human observers do not seem to know the maximum number of the degrees of freedom in a system that we can still keep track of. A photon is certainly a quantum system from our point of view, a simple atom too, a
is not computable. We as human observers do not seem to know the maximum number of the degrees of freedom in a system that we can still keep track of. A photon is certainly a quantum system from our point of view, a simple atom too, a
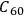 perhaps as well, albeit seeing quantum effects with fullerenes is not easy. But we have never seen a quantum system having, say,
perhaps as well, albeit seeing quantum effects with fullerenes is not easy. But we have never seen a quantum system having, say,
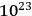 degrees of freedom. So where does the border run? Is it a number like 6 or 20 or is it
degrees of freedom. So where does the border run? Is it a number like 6 or 20 or is it
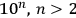 ? All we can say is that mathematics shows that human observers cannot compute their own
? All we can say is that mathematics shows that human observers cannot compute their own
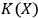 .
.
5 Elements of Reality
Ever since the EPR paper Einstein et.al. 1935, the question of what is real in the quantum world has been at the forefront of all conceptual discussions about quantum theory. Einstein, Podolsky and Rosen formulated their question with regard to physical properties: e.g., is position or momentum real? This is, however, not the only problem of reality that appears when many observers enter the game. Imagine a sequence of observers
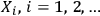 , each identifying systems
, each identifying systems
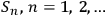 . System identifications of each
. System identifications of each
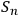 do not have to coincide as some observers may have their Kolmogorov complexity
do not have to coincide as some observers may have their Kolmogorov complexity
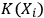 below, or close to,
below, or close to,
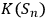 , and others much bigger than
, and others much bigger than
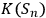 . If there is disagreement, is it possible to say that the systems are real, or objects of quantum mechanical investigation, in some sense? We can encode the binary identification string produced by each observer in his SIA capacity as some random variable
. If there is disagreement, is it possible to say that the systems are real, or objects of quantum mechanical investigation, in some sense? We can encode the binary identification string produced by each observer in his SIA capacity as some random variable
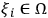 , where
, where
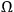 is the space of such binary identification strings, possibly of infinite length. Index
is the space of such binary identification strings, possibly of infinite length. Index
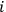 is the number of the observer, and the values taken by random variable
is the number of the observer, and the values taken by random variable
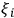 bear index
bear index
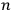 corresponding to “
corresponding to “
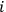 -th observer having identified system
-th observer having identified system
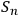 .” Adding more observers, and in the limit
.” Adding more observers, and in the limit
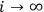 infinitely many observers, provides us with additional identification strings. Putting them together gives a stochastic process
infinitely many observers, provides us with additional identification strings. Putting them together gives a stochastic process
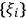 , which is an observation process by many observers. If systems
, which is an observation process by many observers. If systems
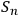 are to have a meaning as “elements of reality,” it is reasonable to require that no uncertainty be added with the appearance of further observers, i.e., that this stochastic process have entropy rate equal to zero:
are to have a meaning as “elements of reality,” it is reasonable to require that no uncertainty be added with the appearance of further observers, i.e., that this stochastic process have entropy rate equal to zero:
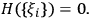
|
2 |
We also take this process to be stationary and ergodic so as to justify the use of Shannon entropy.
Let us illustrate the significance of condition (2) on a simplified example. Suppose that
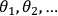 is a sequence of independent identically distributed random variables taking their values among binary strings of length
is a sequence of independent identically distributed random variables taking their values among binary strings of length
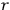 with probabilities
with probabilities
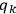 ,
,
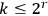 . These
. These
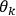 can be seen as identifications, by different SIAs, of different physical systems, i.e., a special case of the
can be seen as identifications, by different SIAs, of different physical systems, i.e., a special case of the
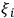 -type sequences having fixed length and identical distributions. For instance, we may imagine that
-type sequences having fixed length and identical distributions. For instance, we may imagine that
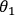 is a binary encoding of the first observer seeing an electron and
is a binary encoding of the first observer seeing an electron and
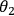 is a binary string corresponding to the second observer having identified a physical system such as an elephant; and so forth. Entropy becomes simply:
is a binary string corresponding to the second observer having identified a physical system such as an elephant; and so forth. Entropy becomes simply:
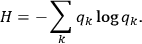
|
3 |
Condition (2) applied to entropy (3) means that all observers output one and the same identification string of length
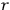 , i.e., all SIAs are identical.
This deterministic system identification, of course, obtains only under the assumption that the string length is fixed for all observers and their random variables are identically distributed, both of which are not plausible in the case of actual quantum mechanical observers. So rather than requiring identical strings we impose condition (2) as a criterion of the system being identified in the same way by all observers, i.e., it becomes a candidate quantum mechanical “object of investigation.”
, i.e., all SIAs are identical.
This deterministic system identification, of course, obtains only under the assumption that the string length is fixed for all observers and their random variables are identically distributed, both of which are not plausible in the case of actual quantum mechanical observers. So rather than requiring identical strings we impose condition (2) as a criterion of the system being identified in the same way by all observers, i.e., it becomes a candidate quantum mechanical “object of investigation.”
6 Relativity of Observation
Let us explore the consequences of condition (2). Define a binary sequence
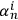 as a concatenation of the system identifications strings of systems
as a concatenation of the system identifications strings of systems
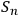 by different observers:
by different observers:
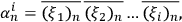
|
4 |
where index
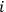 numbers observers and the upper bar corresponds to “string concatenation” (a detailed definition can be found in Zvonkin and Levin 1970). Of course, this concatenation is only a logical operation and not a physical process. A theorem by Zvonkin and Levin 1970 conjectured by Zvonkin and Levin 1970 affirms that the Kolmogorov complexities of strings
numbers observers and the upper bar corresponds to “string concatenation” (a detailed definition can be found in Zvonkin and Levin 1970). Of course, this concatenation is only a logical operation and not a physical process. A theorem by Zvonkin and Levin 1970 conjectured by Zvonkin and Levin 1970 affirms that the Kolmogorov complexities of strings
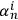 converge towards entropy:
converge towards entropy:
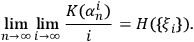
|
5 |
For a fixed
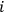 and the observer
and the observer
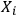 who observes systems
who observes systems
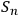 that are quantum in the sense of Definition 6.1, variation of
that are quantum in the sense of Definition 6.1, variation of
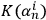 in
in
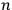 is bounded by the observer's own complexity in his SIA capacity:
is bounded by the observer's own complexity in his SIA capacity:

|
6 |
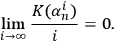
|
7 |
This entails that the growth of
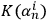 in
in
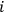 cannot be faster than logarithmical.
Therefore, we have the following:
cannot be faster than logarithmical.
Therefore, we have the following:
Proposition 8.1: An element of reality that may become an object of quantum mechanical investigation can be defined only with respect to a class of not very different observers.
To give an intuitive illustration, imagine adding a new observer
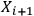 to a group of observers
to a group of observers
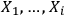 who identify systems
who identify systems
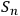 . This adds a new identification string that we glue at the end of concatenated string
. This adds a new identification string that we glue at the end of concatenated string
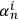 consisting of all
consisting of all
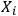 's identifications of
's identifications of
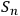 , thus obtaining a new string
, thus obtaining a new string
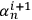 . The Kolmogorov complexity of
. The Kolmogorov complexity of
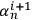 does not have to be the same as the Kolmogorov complexity of
does not have to be the same as the Kolmogorov complexity of
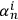 ; it can grow, but not too fast, i.e., not faster than the logarithm. Adding a new observation may effectively add some new non-compressible bits, but not too many such bits. If this is so, then
; it can grow, but not too fast, i.e., not faster than the logarithm. Adding a new observation may effectively add some new non-compressible bits, but not too many such bits. If this is so, then
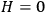 still obtains. Although observers
still obtains. Although observers
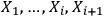 produce slightly different identification strings, they agree, simply speaking, that an atom is an atom and not something that looks more like an elephant.
produce slightly different identification strings, they agree, simply speaking, that an atom is an atom and not something that looks more like an elephant.
The above reasoning applies only to quantum systems
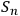 in the sense of Definition 6.1. This is because in the case of classical systems different observers may each operate their own coarse-graining, keeping only some degrees of freedom. System identification strings may then differ dramatically and one cannot expect
in the sense of Definition 6.1. This is because in the case of classical systems different observers may each operate their own coarse-graining, keeping only some degrees of freedom. System identification strings may then differ dramatically and one cannot expect
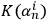 to grow moderately.
to grow moderately.
7 Experimental Test
A previously suggested experimental connection between thermodynamics and theories based on Kolmogorov complexity is based on observing the consequences of a change in the system's state Zvonkin and Levin 1970. Zurek introduced the notion of physical entropy
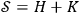 , where
, where
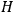 is the thermodynamic entropy and
is the thermodynamic entropy and
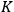 the Kolmogorov entropy. If the observer with a finite memory has to record the changing states of the quantum system, then there will be a change in
the Kolmogorov entropy. If the observer with a finite memory has to record the changing states of the quantum system, then there will be a change in
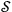 , like the one depicted in Figure 3, and it will lead to heat production that can be observed experimentally.
, like the one depicted in Figure 3, and it will lead to heat production that can be observed experimentally.
 changes.
changes.Fig. 3: Experiment leading to heat production when physical entropy
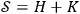 changes.
changes.
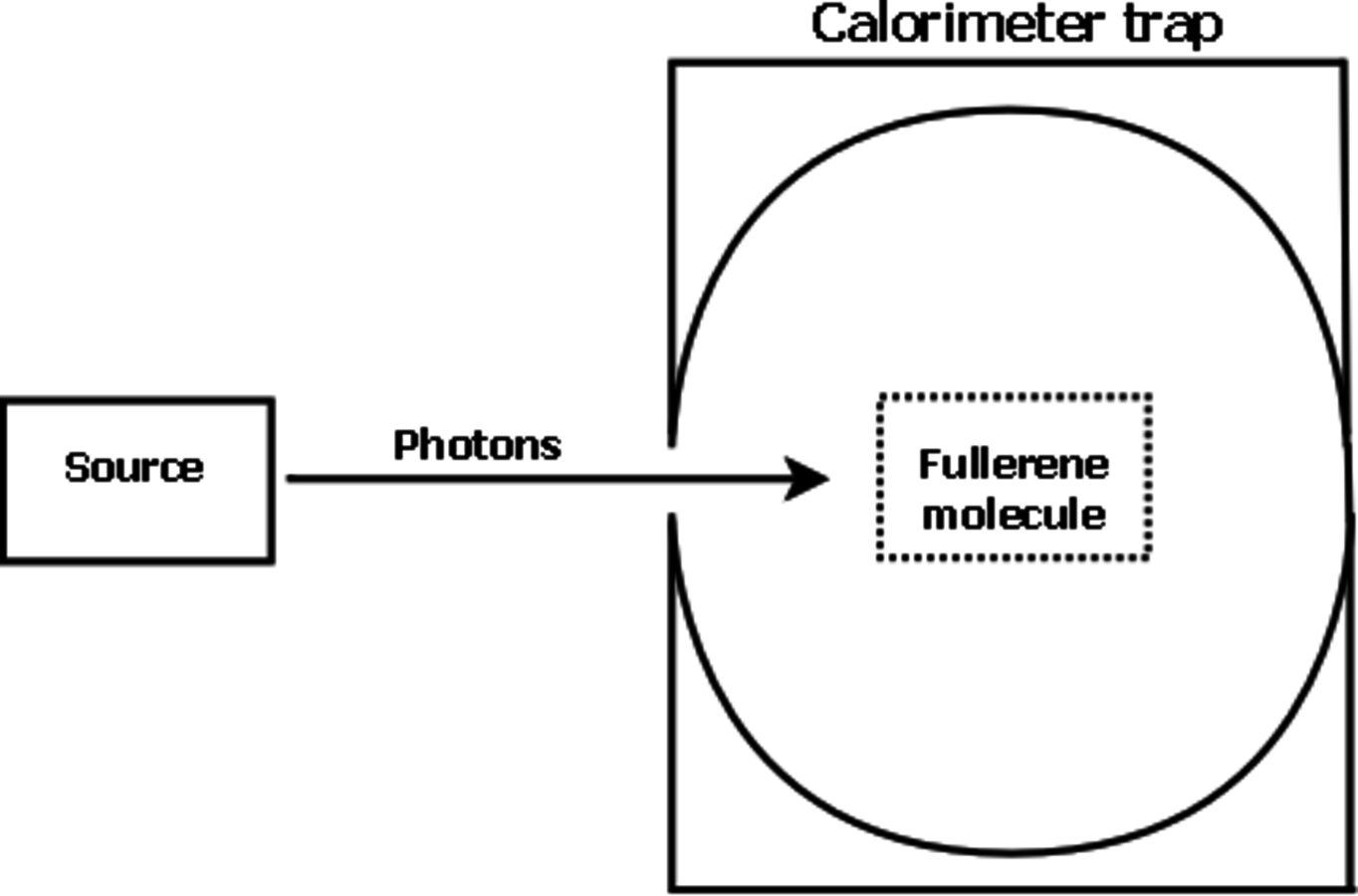
Fig. 4: Experiment leading to heat production when observer's memory becomes saturated.
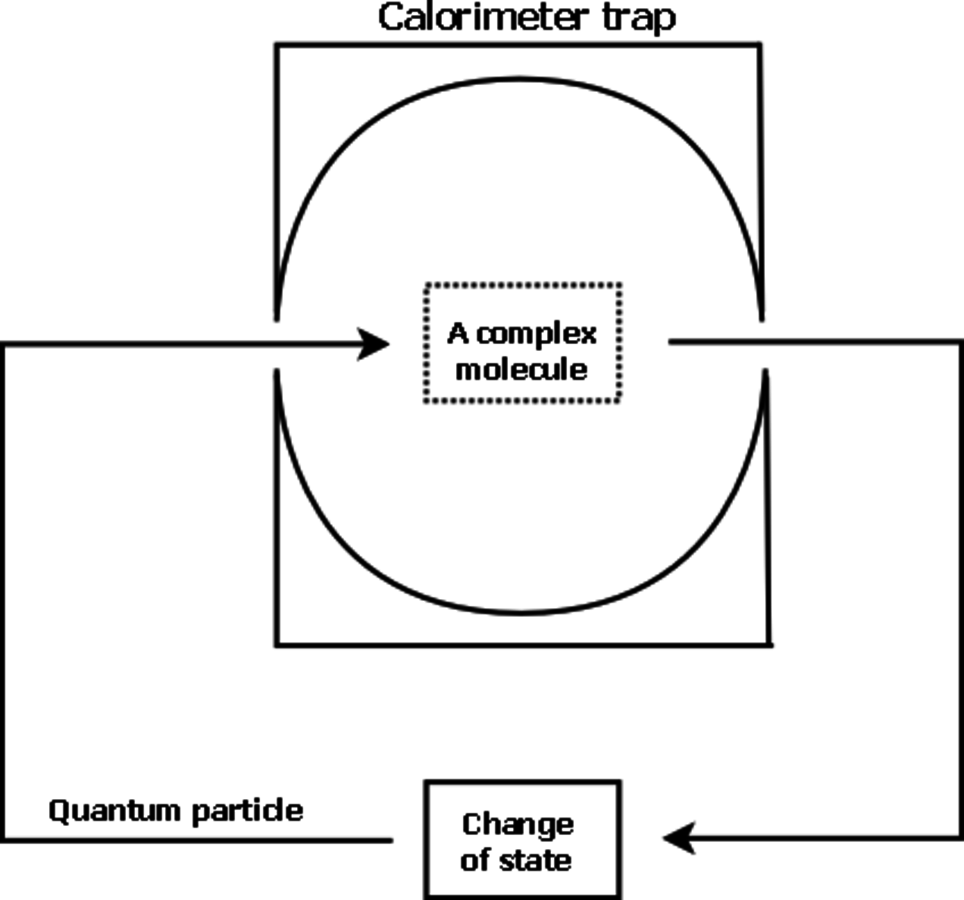
What we propose here, based on a suggestion by Anton Zeilinger, is a simpler setting that can still serve as a test of the universal observer hypothesis. It does not rely on the measurement of particular states, but on the fact of measurement as such. If a measurement occurs, then the observer has identified the quantum system, and this fact in itself, if repeated, will eventually lead to heat production.
An individual fullerene molecule is placed in a highly sensitive calorimeter and bombarded with photons, which play the role of quantum systems with low
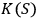 (Figure 4). According to the universal observer hypothesis, the fullerene is a quantum mechanical observer with
(Figure 4). According to the universal observer hypothesis, the fullerene is a quantum mechanical observer with
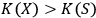 . Thus the absorption of the photon by the fullerene can be described as measurement: the fullerene identifies a quantum system, i.e. the photon, and observes it, obtaining new information. Physically, this process amounts to establishing a correlation between the photon variables, i.e., its energy, and the degrees of freedom of the fullerene. The external observer knows that such a process has occurred but remains unaware of its exact content, so that he is aware that there has been measurement, but doesn't know a precise state of the photon as measured by the fullerene, nor a precise state of the fullerene after measurement.
. Thus the absorption of the photon by the fullerene can be described as measurement: the fullerene identifies a quantum system, i.e. the photon, and observes it, obtaining new information. Physically, this process amounts to establishing a correlation between the photon variables, i.e., its energy, and the degrees of freedom of the fullerene. The external observer knows that such a process has occurred but remains unaware of its exact content, so that he is aware that there has been measurement, but doesn't know a precise state of the photon as measured by the fullerene, nor a precise state of the fullerene after measurement.
Informationally speaking, the same process can be described as storing information in the fullerene's memory. If measurement is repeated on several photons, more such information is stored, so that at some point total Kolmogorov complexity will approach
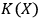 . When it reaches
. When it reaches
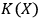 , the fullerene will stop identifying incoming photons as quantum systems. Any further physical process will lead to heat production due to the erasure of memory, as prescribed by the Landauer principle that creates information erasure and heat production Landauer 1961. Physically, this process will correspond to a change of state of the carbon atoms that make up the fullerene molecule: the calorimeter will register a sudden increase in heat when
, the fullerene will stop identifying incoming photons as quantum systems. Any further physical process will lead to heat production due to the erasure of memory, as prescribed by the Landauer principle that creates information erasure and heat production Landauer 1961. Physically, this process will correspond to a change of state of the carbon atoms that make up the fullerene molecule: the calorimeter will register a sudden increase in heat when
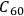 cannot store more information, thereby ending its observer function.
cannot store more information, thereby ending its observer function.
Actual experiments with fullerenes show that this scenario is realistic. A
fullerene molecule “contains so many degrees of freedom that conversion of
electronic excitation to vibrational excitation is extremely rapid.” Thus,
the fullerene is a good candidate for a quantum mechanical observer, for “the
molecule can store large amounts of excitation for extended periods of time
before degradation of the molecule (ionization or fragmentation) is
observed” Lykke and Wurz 1992. The experiments in which fullerenes are
bombarded with photons demonstrate that “the energy of the electronic
excitation as a result of absorption of a laser photon by a molecule is
rapidly converted into the energy of molecular vibrations, which becomes
distributed in a statistical manner between a large number of the degrees of
freedom of the molecule [ ...] The fullerene may absorb up to 10 photons at
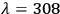 nm wavelength before the dissociation of the molecule into smaller carbon compounds” Eletskii and Smirnov 1995. We read these results as a suggestion that there should be one order of magnitude difference between
nm wavelength before the dissociation of the molecule into smaller carbon compounds” Eletskii and Smirnov 1995. We read these results as a suggestion that there should be one order of magnitude difference between
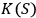 and
and
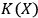 and that this allows the fullerene to act as quantum mechanical observer for up to 10 photons at 308 nm wavelength. What needs to be tested experimentally in this setting is heat production: we conjecture that if the same process occurs inside a calorimeter, the latter will register a sudden increase in heat after the fullerene will have observed 10 photons. What we predict here isn't new physics, but an explanation on a new level, i. e., the level of information, of a physical process, i. e., heat production, which plays a largely overlooked role in the dissociation of fullerenes. We suggest that heat production deserves special attention as a signature of the fullerene's role as quantum mechanical observer.
and that this allows the fullerene to act as quantum mechanical observer for up to 10 photons at 308 nm wavelength. What needs to be tested experimentally in this setting is heat production: we conjecture that if the same process occurs inside a calorimeter, the latter will register a sudden increase in heat after the fullerene will have observed 10 photons. What we predict here isn't new physics, but an explanation on a new level, i. e., the level of information, of a physical process, i. e., heat production, which plays a largely overlooked role in the dissociation of fullerenes. We suggest that heat production deserves special attention as a signature of the fullerene's role as quantum mechanical observer.
As a side remark, imagine that the photon's polarization state in some basis were fully mixed:
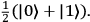 While only the energy of the photon matters during absorption, the external observer records von Neumann entropy
While only the energy of the photon matters during absorption, the external observer records von Neumann entropy
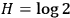 corresponding to this mixture (the initial state of the fullerene is assumed fully known). After absorption, it is mandatory that this entropy be converted into Shannon entropy of the new fullerene state, corresponding nicely to the uncertainty of the external observer in describing the “statistical manner” of the distribution over a large number of the degrees of freedom. From the internal point of view, we may assume perfect `self-knowledge' of the observer, which puts his Shannon entropy equal to zero. However, his Kolmogorov entropy will increase as a result of recording the measurement information Zurek 1989a. Heat produced during the erasure of measurement information is at least equal to Kolmogorov complexity of the string that was stored in observer's memory; but according to quantum mechanics, this heat will not reveal to the external observer any information about the precise photon state observed by the fullerene.
corresponding to this mixture (the initial state of the fullerene is assumed fully known). After absorption, it is mandatory that this entropy be converted into Shannon entropy of the new fullerene state, corresponding nicely to the uncertainty of the external observer in describing the “statistical manner” of the distribution over a large number of the degrees of freedom. From the internal point of view, we may assume perfect `self-knowledge' of the observer, which puts his Shannon entropy equal to zero. However, his Kolmogorov entropy will increase as a result of recording the measurement information Zurek 1989a. Heat produced during the erasure of measurement information is at least equal to Kolmogorov complexity of the string that was stored in observer's memory; but according to quantum mechanics, this heat will not reveal to the external observer any information about the precise photon state observed by the fullerene.
8 Conclusion
The Copenhagen view of quantum mechanics traditionally described quantum systems and observers, epistemologically, as belonging to different categories. On the contrary, the view based on the relativity of observation, as proposed by Everett and later Rovelli, puts all systems on equal grounds and ascribes them only relative states. These two views are not as contradictory as they may seem. Relativity of observation has been understood by some proponents of the Copenhagen school Hermann 19352, (Fock 1971a, 1971a,b). Information-theoretic treatment of the observer gives a chance to completely overcome the tension. On the one hand, the observer is an SIA and is characterized by its Kolmogorov complexity. On the other hand, quantum mechanics can be reconstructed from information-theoretic axioms and thus seen as a theory of information Grinbaum 2007. This puts all systems on equal grounds, in the spirit of Rovelli, while emphasizing the idea of relativity of observation, in the spirit of Fock.
Additionally, information-theoretic treatment of the observer provides a somewhat surprising result developing EPR's notion of “element of reality.” One can make sense of a system existing independently of observation, with respect to a class of observers whose Kolmogorov complexities may differ, even if slightly. Equation (7) provides a mathematical criterion for this.
We have analyzed the observer as a system identification algorithm in the context of quantum mechanics. It remains an open question to apply this analysis to quantum field theory, where the task of system identification may look significantly different from the finite-dimensional situation. It also remains an open problem to realize experimentally the setup proposed in Section 7, which may lead to experimental confirmation of the universal observer hypothesis. Putting together this experimental test, which may show that a fullerene can act as an observer for up to 10 photons, and the remark on non-computability of
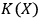 at the end of Section 4 begs yet another question: is it possible to say that, although
at the end of Section 4 begs yet another question: is it possible to say that, although
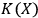 isn't computable in the mathematical sense, physical experiment effectively computes it?
isn't computable in the mathematical sense, physical experiment effectively computes it?
Acknowledgments
I am grateful to Vasily Ogryzko for stimulating discussions and to Časlav Brukner, Markus Aspelmeyer, Ognyan Oreshkov and Anton Zeilinger for their remarks and hospitality at the Institute for Quantum Optics and Quantum Information of the Austrian Academy of Sciences.
References
Bell, J. (1990). Against measurement. Physics World 3: 33-40
Bohm, D. (1971). On Bohr's views concerning the quantum theory. In: Quantum Theory and Beyond Ed. by T. Bastin. 33-40
Bohr, N. (1934). Atomic Theory and the Description of Nature..
Brudno, A. (1978). The complexity of the trajectories of a dynamical system. Russ. Math. Surveys 33: 197-198
- (1983). Entropy and the complexity of the trajectories of a dynamical system. Trans. Moscow Math. Soc. 2: 157-161
Dirac, P. (1930). The Principles of Quantum Mechanics..
Einstein, A., B. Podolsky, B. P. (1935). Can quantum-mechanical description of physical reality be considered complete?. Phys. Rev. 47: 777-780
Eletskii, A. V., B. M. Smirnov (1995). Fullerenes and carbon structures. Physics-Uspekhi 38: 935-964
Erez, N., G. Gordon, G. G., Nest G. (2008). Thermodynamic control by frequent quantum measurements. Nature 452: 724-727
Everett, H. (1957). “Relative state” formulation of quantum mechanics. Rev. Mod. Phys. 29: 454-462
Fock, V. (1971a). The principle of relativity with respect to observation in modern physics. Vestnik AN SSSR 4: 8-12
Friedman, M. (2001). Dynamics of Reason..
George, A. (1953). Louis de Broglie, physicien et penseur..
Grinbaum, A. (2007). Reconstruction of quantum theory. British Journal for the Philosophy of Science 58: 387-408
Henderson, J. R. (2010). Classes of Copenhagen interpretations: Mechanisms of collapse as typologically determinative. Studies In History and Philosophy of Modern Physics 41: 1-8
Hermann, G. (1935). Die naturphilosophischen Grundlagen der Quantenmechanik. Abhandlungen der Fries'schen Schule 6: 75-152
Howard, D. (1994). What makes a classical concept classical? Toward a reconstruction of Niels Bohr's philosophy of physics. In: Niels Bohr and Contemporary Philosophy Ed. by J. Faye, H. Folse. 201-229
Jammer, M. (1974). The Philosophy of Quantum Mechanics..
Kolmogorov, A. (1965). Three approaches to the definition of the concept `quantity of information'. Probl. Inform. Transm. 1: 3-7
Landau, L., E. Lifshitz (1977). Quantum mechanics..
Landauer, R. (1961). Irreversibility and heat generation in the computing process. IBM Journal of Research and Development 5: 183-191
London, F., E. Bauer (1939). La théorie de l'observation en mécanique quantique. Paris: Hermann.
Lykke, K. R., P. Wurz (1992). Direct detection of neutral products from photodissociated . Journal of Physical Chemistry 96: 3191-3193
Peres, A. (1986). When is a quantum measurement?. Am. J. Phys. 54: 688-692
Rovelli, C. (1996). Relational quantum mechanics. Int. J. of Theor. Phys. 35: 1637-1678
von Neumann, J. (1932). Mathematische Grundlagen der Quantenmechanik. Berlin: Springer.
Wheeler, J. (1983). Law without law.
Wheeler, J., W. Zurek (1983). Quantum Theory and Measurement..
Wigner, E. (1961). Remarks on the mind-body question. In: The Scientist Speculates Ed. by I. Good. London: Heinemann 284-302
- (1976). Interpretation of quantum mechanics. Lectures given in the Physics Department of Princeton University.
Zurek, W. (1989a). Algorithmic randomness and physical entropy. Phys. Rev. A 40: 4731-4751
- (1989b). Thermodynamic cost of computation, algorithmic complexity and the information metric. Nature 341: 119-124
- (1998). Decoherence, chaos, quantum-classical correspondence, and the algorithmic arrow of time. Physica Scripta T76: 186-198
Zvonkin, A., L. Levin (1970). The complexity of finite objects and the development of the concepts of information and randomness by means of the theory of algorithms. Russ. Math. Surveys 25: 83-124
Footnotes
English translation in Wheeler and Zurek 1983, 218–259.
Quoted by Jammer 1974, 207–211.