11 Quantum Mechanics in Context:
Pascual Jordan's 1936 Anschauliche Quantentheorie

11.1 Introduction

Pascual Jordan’s 1936, Anschauliche Quantentheorie: Eine Einführung in die moderne Auffassung der Quantenerscheinungen (Jordan 1936a), is an unusual and complicated textbook authored by an unusual and complicated working physicist in an unusual and complicated setting. Jordan was one of the founders of modern quantum mechanics and quantum field theory, but by 1936 he was no longer a major contributor to quantum physics, his attention and effort being diverted, in part, by a growing interest in the relationship between biology and quantum physics. Jordan had been a member of the Nazi party since 1933 and for some years before that had published conservative philosophical and cultural screed under the pseudonym, “Ernst Domeier,” in the journal Deutsches Volkstum (Beyler 2009), but he remained an ardent supporter of modern theoretical physics, openly promoting the work of Albert Einstein, Niels Bohr, Max Born, and other Jewish physicists, in a political setting often inhospitable to jüdische Physik (Beyler 1994; Wise 1994; Hoffmann 2003; Hoffmann and Walker 2007). Moreover, Jordan was still, in 1936, openly allied with the left-leaning Vienna Circle, vigorously promoting his somewhat idiosyncratic version of positivist empiricism, publishing in the Vienna Circle’s journal, Erkenntnis (Jordan 1934; 1935b), and having his work extensively debated there.¹ On the other hand, he wrote a secret report for the Nazi authorities about the political orientation of participants in the Vienna Circle’s Second International Congress for the Unity of Science, which met in Copenhagen in June 1936. This was immediately after he finished, in May 1936, the manuscript of Anschauliche Quantentheorie, which, ironically, includes frequent, generous praise for Bohr, one of the hosts of the Copenhagen conference (Hoffmann 1988).

The book, Anschauliche Quantentheorie, embodies as many tensions and complexities as does its author. As the title suggests, the book aims to provide an intuitive introduction to the quantum theory, explicitly analogous to the intuitive introduction to geometry then famously on offer in David Hilbert and Stephan Cohn-Vossen’s Anschauliche Geometrie (Hilbert and Cohn-Vossen 1933). In this aim it succeeds, after a fashion, but with “intuitive” being persuasively defined in consonance with Jordan’s positivist empiricism as meaning that the theory is developed and expounded on the basis of definitive empirical evidence and not that it is presented by means of something like intuitive pictures. But the Jordan who was distinguished among his physics peers by his mathematical facility and his training in abstract algebra also provides, in the middle chapter 3, a concise and elegant exposition of quantum mechanics from a fundamental, mathematical point of view. Jordan suggests that the possibility of a refined, closed, mathematical formulation of the theory is further evidence of its essential correctness. The core physics chapters are wrapped in an introduction and a concluding chapter that portray the modern quantum theory as an inevitable consequence and vindication of Jordan’s version of positivist empiricism. As well, quantum theory and positivism, taken together, are represented as an expression and vindication of the central tenets of what will come to be known as the Copenhagen interpretation, by which Jordan means, most importantly, Bohr’s correspondence and complementarity principles. And considerable space is devoted to exploring the relationship between quantum mechanics and biology, with Jordan advocating a kind of descriptivist (and thus, positivist) vitalism, sanction for which is also sought in Bohr’s suggestion of a complementarity between vitalism and mechanism. Today’s reader might be surprised to find the book ending with a few sympathetic words for scientific research on telepathy.

It is difficult to gauge the audience for and impact of Jordan’s Anschauliche Quantentheorie. There was no English translation, nor was there a second edition. The German edition had a limited circulation in North America after being reprinted in 1946 by J. W. Edwards, of Ann Arbor, under the Alien Property Act. For the German-speaking audience it would have competed mainly with the 1929 Wellenmechanische Ergänzungsband of the fifth edition of Arnold Sommerfeld’s Atombau und Spektrallinien (Sommerfeld 1929), Jordan’s own earlier 1930 book, co-authored with Max Born, Elementare Quantenmechanik (Born and Jordan 1930), Werner Heisenberg’s 1930 introductory book, Die physikalischen Prinzipien der Quantentheorie (Heisenberg 1930), Werner Bloch’s 1930 German translation of Paul Dirac’s The Principles of Quantum Mechanics (Dirac 1930a; 1930b), Wolfgang Pauli’s 1933 Handbuch article, “Die allgemeinen Prinzipien der Wellenmechanik” (Pauli 1933), and perhaps, John von Neumann’s 1932 Mathematische Grundlagen der Quantenmechanik (von Neumann 1932). It would have enjoyed, along with Heisenberg’s book, the advantage of ease of access and a clear, pedagogical style. Over all of these competitors, it would have enjoyed the advantage of offering, at the time, the most comprehensive and comprehensible, elementary introduction to the developing areas of relativistic quantum mechanics, quantum electrodynamics, second quantization, and quantum field theory. More of an audience might also have been won for the book by the more or less simultaneous appearance of Jordan’s popular book, Die Physik des 20. Jahrhunderts (Jordan 1936b). But some of Jordan’s physics colleagues would have been put off by the book’s philosophical agenda, and its potential as a university textbook would have been limited by its unabashed presentation of Einstein and relativity theory at a time when Heisenberg, for example, was being branded a “white Jew” in the pages of the SS journal, Das Schwarze Korps, for his continuing to teach relativity in Leipzig, see (Cassidy 1992, 381).

Still, Jordan’s Anschauliche Quantenmechanik stands out and deserves our attention as one of the most important textbooks of its era precisely because of all the tensions and complexities it embodies, it being, in this respect a reflection of its times, and also because its author was, along with Sommerfeld, Born, Heisenberg, Pauli, and Dirac, one of the most important shapers of modern quantum mechanics.

11.2 Pascual Jordan in 1936

That Jordan never won a Nobel Prize in physics is a puzzle. Some blame his inability to give elegant lectures because of a stutter; some blame his pro-Nazi politics or his support, after World War II, for a German nuclear weapons program; some blame the fact that Born misplaced Jordan’s 1925 manuscript in which Fermi-Dirac statistics were first presented, thus depriving the modest Jordan of his rightful claim to priority over Pauli (Schroer 2007). But the fact remains that his contributions to the development of modern quantum theory were as fundamental and far-reaching as those of many whose achievements were recognized with a Nobel Prize. It was Jordan, more than anyone else, who developed a mathematically elegant formulation of matrix mechanics (Born and Jordan 1925; 1926). It was Jordan who went on to consolidate matrix mechanics with Dirac’s alternative operator calculus (Dirac 1925) and Erwin Schrödinger’s wave-mechanical formulation (Schrödinger 1926a; 1926b) in the comprehensive formalism known as statistical transformation theory (Jordan 1927a; 1927b, see also Duncan and Janssen 2009). It was Jordan who did more than anyone other than Dirac to inaugurate the program of quantum field theory, in ways such as developing the second quantization approach and being the first to discover the problem of divergences in quantum field theory (Jordan and Klein 1927; Jordan and Wigner 1928). And it was Jordan who, along with von Neumann and Eugene Wigner, was developing more abstract algebraic frameworks for quantum mechanics (Jordan 1933b; Jordan et.al. 1934). Not without reason has Jordan been described as “the unsung hero among the creators of quantum mechanics” (Schweber 1994, 5).

But by May of 1936, when Jordan completed work on the manuscript of Anschauliche Quantentheorie, his most significant contributions to the quantum theory were in the past. Jordan was then developing an interest in the relationship between physics and biology, an interest that first found expression in his 1932 paper, “Die Quantenmechanik und die Grundprobleme der Biologie und Psychologie” (Jordan 1932, see also Jordan 1934), and would continue to the end of his life. An interest in the relationship between biology and physics was shared with a number of other physicists who had worked on quantum theory, such as Schrödinger, whose What Is Life? appeared in 1944 (Schrödinger 1944), and Max Delbrück, who had turned to biophysics at Bohr’s urging and, in 1935, had laid the foundations of modern genetics with the famous Dreimännerarbeit, “Über die Natur der Genmutation und der Genstruktur.”² Jordan had not stopped doing physics, however. Later he would turn to work on gravitation, general relativity, and cosmology, see, for example, (Jordan 1955), and he continued to publish on mathematical physics and the logical and conceptual foundations of quantum mechanics.³

One year before completing his manuscript Jordan had been promoted to Ordinarius at Rostock University, at the comparatively young age of thirty-two. But Rostock, where Jordan had worked since his appointment as Extraordinarius in 1929, was not the kind of high-status post one might have expected for a physicist of such early achievement and promise. Jordan’s stutter, which made lecturing difficult, was surely part of the reason for this. After 1933, his awkward relationship with the Nazi party—a party member but a dissenter from the assault on Jewish physics—would have been an added impediment to a call to a more prestigious chair.

Jordan’s early training in physics and mathematics was at the Technische Hochschule in his native Hannover. In 1923 he went to Göttingen, where he did a dissertation under Born (Jordan 1924). Between 1924 and 1926, he was an Assistent first to the mathematician, Richard Courant, and then to Born. He did his Habilitation in 1926, was for one year a Privatdozent in Göttingen, then moved to Hamburg as Privatdozent in 1927, before getting the call to Rostock in 1929. During his most productive years in Göttingen, between 1925 and 1927, not only did he collaborate with Born and Heisenberg on the mathematics of matrix mechanics and develop, largely on his own, statistical transformation theory, he also co-authored with James Franck a book on the excitation of quantum transitions by collisions (Franck and Jordan 1926).

It was not just physics, however, that drew Jordan’s attention in Göttingen. As mentioned, he was trained in mathematics and was, briefly, an Assistent with Courant. The Göttingen mathematics tradition centered around David Hilbert had a major influence on the development of Jordan’s thinking. The Hilbert program sought to place mathematics on a logically and conceptually secure foundation by first formulating mathematical theories axiomatically and then demonstrating the correctness, consistency, and completeness of such axiomatic theories by finitistic means. The famous early expression of the program was Hilbert’s own axiomatic formulation of geometry (Hilbert 1899), but greater urgency attached to the program’s extension to set theory and analysis, where, it was recognized, methodological clarity and rigor were needed to allay the fear that fatal inconsistencies might undermine such achievements as Cantor’s elaboration of the transfinite hierarchy. Hilbert’s key insight was that the consistency of theories describing infinities might be proven by finite means if one recast the problem syntactically, which is to say as a problem of proving that no contradiction could be derived within an axiomatic formulation of theory. Since a proof is a finite list of finite strings of symbols, reasoning about proofs should, itself, be a finite mental operation, essentially nothing more complicated than counting. Hilbert was famous, also, for promoting the extension of this program to mathematical physics. Not only did he and Courant coauthor one of the era’s most influential textbooks on mathematical physics (Courant and Hilbert 1931–1937), but Hilbert also actively recruited the involvement of the Göttingen physics community in the work of his mathematics institute. Göttingen was one of the few places in the world where a mathematically sophisticated young physicist like Jordan could have been produced and could have flourished.⁴

Another major influence on Jordan was the development of logical empiricism and the Vienna Circle.⁵ Claiming the heritage of Ernst Mach, the movement known as the Vienna Circle is commonly regarded as having been born in 1922, when Moritz Schlick arrived in Vienna to take up Mach’s vacant chair. By the early-to-mid 1930s, the Vienna Circle had become a major intellectual force, with its own journal, Erkenntnis, its own book series, and sponsorship of a series of international congresses. It was allied with other influential groups, including the Berlin Gesellschaft für wissenschaftliche Philosophie, centered around Hans Reichenbach. The movement aimed to continue the intellectual legacy of the philosopher, historian, and physicist, Ernst Mach, while refining and elaborating Mach’s positivist philosophical program with the powerful new tools of symbolic logic in order to craft a new kind of empiricism that would be adequate to the task of legitimating the achievements of modern theoretical physics—especially Einstein’s theory of general relativity—in the face of threats posed by traditional philosophical critiques of the revolutionary new physics, foremost among them critiques derived from various versions of neo-Kantianism and traditional metaphysics.⁶

The movement was heavily involved with theoretical physics. Schlick had taken his Ph.D. in physics with Max Planck in Berlin in 1904, and many of his earliest and most influential philosophical works concerned the philosophical implications of relativity theory.⁷ Other major figures associated with the Vienna Circle were similarly engaged with physics. Philipp Frank was trained in physics under Ludwig Boltzmann in Vienna. He was Einstein’s successor in physics at Prague in 1912 and later published a major study of the quantum theory’s implications for causality (Frank 1932). Rudolf Carnap wrote his Jena doctoral dissertation on the problem of space in general relativity (Carnap 1921). Hans Reichenbach’s first three books concerned the conceptual foundations and axiomatic formulation of relativity theory (Reichenbach 1920; 1924; 1928). But it was not only the logical empiricists who were so strongly oriented toward theoretical physics at the beginning of the twentieth century. The Marburg neo-Kantian tradition was similarly deeply engaged with physics, a high point being Ernst Cassirer’s analysis of relativity theory from a neo-Kantian point of view (Cassirer 1921). But it was the Vienna Circle and logical empiricism, more than any other period philosophical movement, that claimed the title of philosophical champion of modern theoretical physics.⁸

That a young physicist like Jordan, with a broad-ranging and restive intellect, should be drawn to logical empiricism is, thus, not very surprising. Many of Jordan’s contemporaries evinced similarly strong philosophical interests, though not all of them followed Jordan in his attachment to positivism. Pauli, who was Mach’s godson (literally), was perhaps closest to Jordan’s philosophical orientation (Enz 2002). Heisenberg claimed that his discovery of matrix mechanics was inspired by an empiricist resolve to disavow the search for picturable models of the internal structure of the atom and focus, instead, on seeking only mathematical relationships among “observables” like the frequency (color) and intensity (brightness) of spectral lines, but he combined with this a deep sympathy for an Aristotelian metaphysics of act and potency (Camilleri 2009). Whatever their differences, many of Jordan’s contemporaries agreed that the road to the relativity and quantum revolutions was made easier by an empiricist resolve to let go of the traditional metaphysics of space, time, and causality if that is what the empirical facts implied.

As significant as the impacts of Hilbert and the Vienna Circle on Jordan were, more significant still was the impact of Bohr. Unlike Heisenberg, Jordan was never an intimate member of the Bohr circle in Copenhagen. He was, however, a regular visitor and a regular participant in the annual conferences on quantum physics that were a highpoint of Copenhagen physics life in the early-to-mid 1930s. Jordan also made himself one of the most ardent promoters of what he took to be Bohr’s program in quantum physics after 1927. Whether there ever was a unitary Copenhagen interpretation of quantum mechanics and what that interpretation might have been is a contested question.⁹ As we shall see, central to Bohr’s program, on Jordan’s reading, are the correspondence and complementarity principles. But these principles, or at least Bohr’s intended meaning, require interpretation. Is the correspondence principle to be given a strong reading as asserting the existence of a general classical limit to quantum physics or a weak reading as a mere heuristic for finding appropriate quantum analogues to classical systems and behaviors?¹⁰ Is complementarity restricted to conjugate observables within quantum physics, or is a more general epistemological principle intended?¹¹ Yet another question of special relevance to Jordan’s understanding of Bohr’s program is whether Bohr’s interpretation of quantum mechanics assumes a positivist philosophy of science. That such is the case was once a rather widespread view and is still not an uncommon one today, however thin might be the warrant for such a reading in Bohr’s own discussions of complementarity. As we shall see, it might well be that Jordan—a fan of both Vienna and Copenhagen—might bear more than a little responsibility for promoting a positivist version of a Copenhagen interpretation.

A final fact of note about Jordan in 1936 is that, by then, he was no longer hiding his political musings behind a pseudonym. In the series of articles that he had published in the early 1930s in the conservative, nationalist journal, Deutsches Volkstum under the name “Ernst Domeier” (Domeier 1930a; 1930b; 1930c; 1930d; 1931a; 1931b; 1932), Jordan complained about Marxism, secularism, and the baleful cultural effects of liberal democracy of the Weimar variety, and he had championed science and technology as engines of positive social transformation.¹² After Hitler’s ascent to power in 1933, and after Jordan joined the Nazi party in May of that year, he felt comfortable voicing such views under his own name, starting with an article in the spring of 1933 in the Rostock university newspaper on “Die Wandlung der Universität” (Jordan 1933a), and continuing in 1935 in a booklet, Physikalisches Denken in der neuen Zeit (Jordan 1935c), published by the same press that was responsible for Deutsches Volkstum, as well as additional articles in that journal (Jordan 1935a; 1935d). But Jordan did not follow the lead of the anti-Semitic proponents of “Deutsche Physik,” such as Johannes Stark and Philipp Lenard in attacking modern theoretical physics as “Jüdische Physik.”¹³ On the contrary, Jordan vigorously disputed even the more commonplace belief in different national styles in science, a mode of understanding that one could find, for example, in Felix Klein’s otherwise celebrated history of mathematics (Klein 1926–1927). Responding to Klein’s doctoral student, Ludwig Bieberbach, founder of the “Deutsche Mathematik” movement in 1936, Jordan wrote: “The differences among German and French mathematics are not any more essential than the differences between German and French machine guns.”¹⁴ For a while in the middle- to late-1930s, Jordan seems to have paid a professional price for his defense of the ideal of objective science and a theoretical physics independent of nations and races. As the influence of the “Deutsche Physik” movement began to wane, however, Jordan’s academic standing improved, until, in 1942, he was awarded the Planck Medal by the Deutsche Physikalische Gesellschaft and then, in 1944, he was called to Berlin as Max von Laue’s successor.

What is most important for our purposes in Jordan’s political writings is his arguing that science, properly understood—which is to say, interpreted in line with antimetaphysical positivism and Bohr’s principle of complementarity—undermines Marxist materialism and opens the door for both religion and a kind of descriptivist vitalism in biology. It is here, in Jordan’s political writings, that the many different strands of his thinking begin to entwine into a somewhat coherent, if highly idiosyncratic world view. It is the politics that provides the glue. Here is where the physics, the biology, and the philosophy combine. While the politics is kept discreetly in the background in Jordan’s Anschauliche Quantentheorie, understanding the book’s many idiosyncrasies is impossible without an appreciation of the political context.

11.3 The Book

Jordan’s Anschauliche Quantentheorie is a brief, 332 pages, book divided into five chapters

1“Die Grundexperimente der Quantenphysik” [“The Basic Experiments of Quantum Physics”]¹⁵

2“Theoretische Analyse der quantenphysikalischen Grundexperimente” [“Theoretical Analysis of the Basic Experiments of Quantum Physics”]

3“Quanten- und Wellenmechanik” [“Quantum and Wave Mechanics”]

4“Mehrkörpertheorie und Elementarteilchen.” [“Many-body Theory and Elementary Particles”]

5“Atome und Organismen” [“Atoms and Organisms”]

and introduced by seven pages of introduction, Vorbemerkungen (“Preliminary Remarks”). It is not a typical textbook in many respects. It is not, for example, the kind of text from which the novice student will learn how to solve problems. Nor does it aim to provide a comprehensive survey of all major topics. Instead, the book emphasizes conceptual and mathematical fundamentals, though in a manner quite different from von Neumann’s Mathematische Grundlagen der Quantenmechanik (von Neumann 1932), its very organization being driven by the author’s distinctive philosophical agenda. On the other hand, it is, in many ways, an elegant book. In it, Jordan evinces a talent for clear explanation and exposition. It is a book that the sophisticated student can read with profit. For example, I do not recall having seen anywhere else a more lucid introduction to second quantization.

Jordan announces his philosophical agenda in the introduction: “The overall epistemological orientation that finds expression in modern quantum theory—and that, conversely, receives its most significant support from the quantum theory—has been designated by the author in writings on this subject as ‘positivistic’” (Jordan 1936a, vii). What does “positivistic” mean?

What I will defend is the epistemological orientation of Bohr and Heisenberg. For me, the writings of Ernst Mach have formed an indispensable preparation for understanding these modern quantum physical conceptions, and the kinship of Mach’s ideas with them seems to me more essential than the differences. (Jordan 1936a, vii–viii)

That anti-positivists such as Planck, von Laue, and Einstein also dissent from quantum orthodoxy is, for Jordan, further evidence of the deep connections between positivism and quantum theory. Jordan concludes his brief explanation of positivism with an association that will surprise many readers, but that explains the homage intended by the book’s title:

The essential and decisive principle of positivist epistemology—the restriction of admissible propositions to those that can be reduced to experimentally testable propositions—seems to me to be characterizable, furthermore, as a sensible adaptation of the same principle that forms the starting point for Hilbert’s foundational investigations in mathematics, and that Hilbert calls the “finite standpoint.” (Jordan 1936a, viii)

Positivism famously opposes unscientific metaphysics and so is incompatible with “dogmatic materialism.” Jordan warns the reader that some authors confuse the issue by using the term “positivism” in other ways. Philipp Frank, for example, is said to represent a point of view that is a kind of compromise between positivism and materialism, and Bernhard Bavink is even worse, turning “positivism” into a virtual synonym for “materialism.” But clarity on this point is essential, because, on Jordan’s view, positivism and quantum theory together undermine “dogmatic materialism” and so open the way toward a new descriptivist vitalism in biology. Classical physics supported materialism, but quantum physics, especially as interpreted by means of Bohr’s complementarity principle—which not only consummates the development of quantum physics but also “opens a new epoch for our entire natural scientific thought”—drives us toward an “organic view,” whose concepts go beyond the physics of the inorganic and whose laws represent something “essentially new” (Jordan 1936a, ix).

If modern quantum physics is a straightforward expression of positivism, then its content must be fixed in virtually every detail by definitive experimental results. The task of chapter 1, “The Basic Experiments of Quantum Physics,” is to exhibit this empirical basis. What is sought is an

inductive construction¹⁶ of the theory that makes clear the necessary givenness [zwangsläufige Gegebenheit] of its fundamental concepts and fundamental assumptions by means of direct experimental results […] in which the character of quantum physics appears […] pure and undisguised. (Jordan 1936a, 1–2)

No surprise, therefore, that the chapter begins with black-body radiation and the 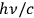Planck formula. But it is a measure of Jordan’s sophistication about fundamentals that the very next topic is wave-particle duality. Jordan starts with the experimental evidence for the corpuscular nature of radiation in the Wien limit, as shown in Einstein’s 1905 analysis of the photoelectric effect, and follows this with the Bothe-Geiger and Compton-Simon experiments. We then turn immediately, however, to interference effects as a prelude to a discussion of de Broglie waves, and their experimental demonstration by electron diffraction and the Ramsauer effect. Later sections take up stationary states, emission, absorption, scattering, and the dynamics of quantization. The language of direct empirical determination is everywhere. The expression for the entropy of radiation in the Wien limit, like the Planck formula itself, is a “directly empirically secured law” (Jordan 1936a, 9). That the light quantum has a momentum of finds a “direct experimental confirmation though investigations into the Compton effect” (Jordan 1936a, 12). Stationary states and the existence of discrete energy levels are first introduced through the Stern-Gerlach and Frank-Hertz experiments. When atomic and molecular spectral data are introduced a few pages later, it is as the “immense empirical material” that “confirms everywhere and without exception the validity of an empirical law,” the Ritz combination principle, which plays a central role in Jordan’s account, and which is further “proven” by the Stark and Zeeman effects (Jordan 1936a, 25–26). “The empirical comparison of absorption and emission intensities for the same spectral line” demonstrates the validity of Einstein’s law relating the probability coefficients for absorption and spontaneous emission. Several experiments provide “direct empirical confirmation” for the adiabatic principle (Jordan 1936a, 44).

With the empirical basis thus secured, Jordan turns in chapter 2 to the “Theoretical Analysis of the Basic Experiments of Quantum Physics.” The main tool is the correspondence principle, which Jordan describes as “the most important idea in all of quantum theory.” Jordan notes that the correspondence principle is not like the energy, entropy, and relativity principles, which are “laws of nature in completely worked out formulation.” It is, instead, “a guide to the detection of still unknown laws of quantum phenomena,” which cannot be given a “mathematically precise expression” (Jordan 1936a, 51). And even now—1936—when we possess a mathematically refined quantum formalism, the correspondence principle is still crucial as a guide in figuring out the “meaning” of the formalism. It does this by exhibiting a “comprehensive and close analogy between classical theory and quantum theory” (Jordan 1936a, 52).

How far Jordan thinks he can push arguments based on the correspondence principle is illustrated by his introduction of electron spin. Analysis of the anomalous Zeeman-effect requires the introduction of the 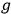Landé factor, , in the expression for the magnetic energy of the electron. A “comprehensive correspondence-like description” (zusammenhängende korrespondenzmäßige Beschreibung) emerges by introducing a second quantum number for the internal angular momentum that takes half-integral values in the doublet case, where 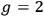. Jordan then writes:

The introduction of this half-integral spin-moment of an electron […] can be characterized as a departure from the image of the electron simply as a mass-point; there exists a certain correspondence-like analogy to a body rotating around an internal axis, in which, in addition to the angular momentum of its center-of-mass motion, there is another angular momentum of the proper rotation. But the significance of this analogy should not be over-valued: Basically, we are concerned here with relationships that cannot be understood according to classical analogies. With respect to the doubling of the statistical weights required by the introduction of the spin-moment, it would be more prudent to speak of a non-classical “two-valuedness” (Pauli). (Jordan 1936a, 100)

One might worry that the correspondence principle has been pressed beyond the breaking point if a “correspondence-like analogy” turns out not really to be an analogy at all.

That there are, of course, limits to the usefulness of classical analogies in quantum physics is an essential part of the other major idea that Bohr introduced, complementarity, the idea in which “the conceptual understanding of quantum phenomena achieves completion” (Jordan 1936a, 115). A preliminary exposition of complementarity, is the subject of the concluding section of chapter 2. The complementarity principle is needed, says Jordan, because the mathematical formalism of quantum physics requires the elaboration of an “intuitive representation of the essential laws.” But since we cannot construct a “model” according to accustomed classical principles, the task is, instead, to produce an “adaptation and customization” of our ideas to the new laws of quantum physics. We should not expect that an “intuitive understanding” will assume an “unalterable maintaining of the customary and the well known” (Jordan 1936a, 114–115).

The exposition that follows is unsurprising in that Jordan presents wave and particle models as complementary descriptions of quantum phenomena, and works out more precisely the examples of position and momentum as well as energy and time as complementary magnitudes. In a standard manner, wholly in the spirit of Bohr, Jordan points to the physical incompatibility of measurement contexts as the basis of complementarity.

Bohr’s own discussions of complementarity, starting with his introduction of the idea in the 1927 “Como” paper (Bohr 1928), have occasioned controversy and confusion. In 1927 he spoke of a complementarity between “space-time co-ordination” and “the claims of causality” (Bohr 1928, 54). The attentive reader of that first paper will notice that Bohr, himself, then explains that the relationship between position and momentum exhibited in the Heisenberg uncertainty principle is a “simple symbolical expression for the complementary nature of space-time description and the claims of causality” (Bohr 1928, 60). But the myth persists that it was only the challenge of the Einstein-Podolsky-Rosen paper in 1935 (Einstein et.al. 1935) that led Bohr to reformulate complementarity as a relationship between arbitrary conjugate observables. It is instructive, therefore, to find Jordan explaining that complementarity was “crystalized” already in the statistical transformation theory that he and Dirac developed in 1927, expressed in the now familiar form of a relationship between observables represented by non-commuting operators, be those position and momentum or components of spin along orthogonal axes. Indeed, when Jordan returns to this issue in chapter 3, he writes that “noncommutativity” acquires an “intuitive meaning” in that it “directly expresses” what is contained in the complementarity principle, namely, the existence of physical magnitudes that can be measured “individually but not simultaneously.” Then, in a footnote, he makes the following startling claim: “In the historical sequence of conceptual developments, the idea of complementarity that was expounded in earlier parts of this book was, conversely, developed by Heisenberg and Bohr out of the Dirac-Jordan theory that is sketched here” (Jordan 1936a, 171). Take a moment to get over the shock of Jordan’s claiming priority for the idea of complementarity, a claim that might well contain a kernel of truth, and realize that, whatever the real history, Jordan’s explication of complementarity by means of the apparatus of statistical transformation theory makes clear the fact that complementarity was widely understood, well before 1935, as a generic fact about the relationship between observables represented by non-commuting operators.

Chapter 3, “Quantum and Wave Mechanics,” is the technical heart of the book. As one might expect from a mathematician such as Jordan, it is written at a comparatively high level of abstraction, though a few standard examples and applications—the harmonic oscillator, angular momentum, the hydrogen atom—are worked out in detail. Nowhere else in the textbook literature available in the mid-1930s would one have found such a succinct, lucid, indeed eloquent presentation of the fundamental mathematics of quantum physics. Matrix and wave mechanics are developed in detail. Their equivalence is demonstrated in a reasonably intuitive way, without the elaborate algebraic apparatus one might have expected from Jordan.¹⁷ The two are then subsumed under the broader framework of statistical transformation theory, and the power of that formalism is exhibited through its application to the problem of electron spin. The level of abstraction was higher still in von Neumann’s Mathematische Grundlagen der Quantenmechanik (von Neumann 1932), but in no way could it be taken to provide an “intuitive” introduction to the theory. Dirac’s Principles of Quantum Mechanics (Dirac 1930a; 1930b) was comparable to Jordan’s chapter 3 in its level of abstraction, but everyone complained about its opacity, as Dirac lacked Jordan’s pedagogical instincts. Born and Jordan’s own 1930 Elementare Quantenmechanik is equally elegant, from a mathematical point of view, but it is far more detailed and thorough in presenting the theory’s mathematical essentials, taking four hundred and forty-eight pages to cover the terrain that Jordan, by himself, covers in a mere forty-nine pages in chapter 3. Jordan’s 1936 textbook stands alone in offering just as much and just as little as the bright student interested in both conceptual and mathematical fundamentals might want.

Chapter 3 presents non-relativistic quantum mechanics in a closed, mathematical form. Chapter 4 turns to the messy business of relativistic quantum mechanics, quantum field theory, and nuclear physics. Jordan had as much or more claim to authority on these topics than any of his contemporaries; still, it was a challenge to write such a chapter in 1936. Dirac had put quantum electrodynamics into reasonably good shape. Jordan himself had further developed the technique of second quantization for matter waves. In 1930, Pauli had introduced the concept of the neutrino to account for the continuous energy spectrum of electrons in beta decay. In 1932 Chadwick had discovered the neutron, and the discovery of the positron in 1933 had finally solved the problem of the negative energy solutions. In 1934 Enrico Fermi had introduced the theory of weak interactions to explain the process of beta decay. And in February of 1936, Bohr had introduced the liquid-drop model of the nucleus. But problems were everywhere, foremost among them the endemic divergences of quantum field theory, a problem for which no one had a solution. In 1935 Hideki Yukawa had postulated the existence of massive bosons to mediate nucleon-nucleon interactions, but a satisfactory theory of the strong nuclear force was decades away.

Jordan does a good job of bringing order to this confused material. His discussions are clear and to the point. Especially nice are the presentations of quantum statistics and second quantization. But Jordan himself emphasizes the incomplete state of things in 1936. He introduces the chapter by declaring, modestly, that its aim is “to make clear how far we have come and what we are still lacking” (Jordan 1936a, 179). The chapter can be read with profit today as a kind of historical snapshot of physics in the making. This is true even with respect to the one bit of self-indulgence that mars an otherwise balanced and dispassionate presentation, namely, the nine pages that Jordan devotes to his own neutrino theory of light, an idea first introduced by de Broglie, according to which the photon might be regarded as a composite particle, made up of a neutrino-antineutrino pair. In fairness, Jordan had made an important contribution by tackling the problem of deriving the correct Bose-Einstein statistics on the basis of this model. Still, while the neutrino theory of light might rightly have, by now, largely disappeared from view, its presentation in chapter 4 simply adds to the chapter’s importance as an historical record of the early years of quantum field theory and particle physics.

A little self-indulgence at the end of chapter 4 is an apt prelude to chapter 5, “Atoms and Organisms,” where the unique intellectual personality of Jordan comes into full view. The chapter contains three sections: § 1. “Die positivistische Methode” [“The Positivistic Method”]; § 2. “Kausalität, Statistik und Finalität” [“Causality, Statistics, and Finality”]; and § 3. “Die Aufbau der realen Welt” [“The Construction of the Real World”].

Section one begins with a reiteration of Jordan’s positivist view of the quantum theory, asserting again, as at the beginning of the book, that the principles of quantum mechanics, at least “within the limits of the non-relativistic theory,” are “unavoidable consequences of the empirically given.” Non-relativistic quantum mechanics is said to constitute “a consistent, closed, conceptual structure in which no fundamental problem remains unsolved and in whose framework every possible question appears as a clearly defined mathematical problem” (Jordan 1936a, 271). But the new theory stands in such “stark contrast” to classical physics that its proper, “intuitive” understanding requires our overcoming of classical “prejudices” through “a thorough, methodological-epistemological analysis” (Jordan 1936a, 272).

Central to that epistemological analysis are two distinctions famously asserted by Vienna Circle logical empiricists: (a) the distinction between genuine problems and “pseudo-problems” (Scheinprobleme) (Carnap 1928); and (b) the distinction between meaningful and meaningless propositions (Carnap 1932). Pseudo-problems are those inaccessible to scientific investigation because of the nature of the scientific method. Mathematics affords many examples of pseudo-problems, such as puzzles about the nature of imaginary numbers and infinitesimals. In physics, says Jordan, we have Bohr to thank, more than anyone else, for “brushing aside countless pseudo-problems” (Jordan 1936a, 273). Jordan’s main example concerns quantum jumps. That we can accurately predict statistical averages for emission intensities might lead one to ask what “remarkable and secret mechanism leads to these peculiar results.” Bohr has emphasized, however, that this is “not to be regarded as something requiring explanation, but as something that is a primitive given [ursprünglich Gegebenes].” He continues:

This view does away with the whole tangled mess [Wust] of the countless, well-known pseudo-problems that must arise out of any attempt to find an explanation for the laws arrived at via the correspondence principle by means of detailed models for the “course” or “mechanism” of quantum jumps. (Jordan 1936a, 276)

Recognizing pseudo-problems as what they are requires, in turn, one’s understanding the distinction between meaningful and meaningless propositions. Meaningful propositions are those that are either true or false, and in such a way that deciding between these alternatives is a “solvable problem.” Moreover, the only meaningful propositions are those “that refer directly to sense experiences” or can be shown to be “equivalent” to such basic empirical propositions through “definitions and terminological stipulations” (Jordan 1936a, 276–277). Einstein’s analysis of distant simultaneity is the famous example from physics, for the assertion that two distant events are simultaneous, without specification of a frame of reference, lacks empirical content.

Jordan’s main reason for promoting this positivist perspective on the epistemology of quantum mechanics is revealed in the next section, “Causality, Statistics, and Finality.” Quantum mechanics is a non-deterministic theory. In this respect it differs fundamentally from the deterministic classical physics of Newton (and Einstein’s relativity theory) that inspired the mechanistic materialism of Laplace. Moreover, as a mathematically closed theory, quantum mechanics can accommodate no “completion” by means of a deterministic model. Jordan cites approvingly von Neumann’s proof of the impossibility of a hidden variables interpretation of theory (von Neumann 1932), adding laconically, in a footnote, that “the objections raised against Neumann’s proof are unfounded” (Jordan 1936a, 283). But with classical determinism thus overthrown by quantum mechanics, the door is opened to a revival of vitalism and teleology in biology.

For a positivist like Jordan, teleology cannot be a metaphysical thesis. It is, instead, a claim about the appropriate descriptive vocabulary for biology. For the description of biological structures and processes the language of purposiveness is “indispensable,” which means, says Jordan, “that the teleological point of view is an indispensable element of biological concept formation” (Jordan 1936a, 287). That the teleological mode of description can be made to work scientifically is further demonstrated by the fact that it can be given clear mathematical formulations. Thus, the idea of purposiveness can be expressed mathematically in the form of variational problems. The related and equally indispensable concept of “wholeness” or the “indivisibility of individual organisms” can be expressed in the form of integral equations (Jordan 1936a, 290–291).

Jordan goes on to discuss an array of more specific questions concerning the relationship between quantum physics and biology. Mendel’s research into combining ratios proves that discreteness plays a fundamental role in biological processes. That random quantum jumps play a role in biology is suggested by the evidence then accumulating for mutations induced by radiation so weak that no more than a single photon could be involved. That randomness at the quantum level can have effects at the biological level is suggested by the possibility of individual, quantum-scale events “directing” mesoscopic and macroscopic biological processes. And if quantum randomness can be “amplified” to the macroscale in this manner, then quantum randomness might be an explanation for our subjective sense of free will. What does this all imply for the fraught question of the reducibility of biology to physics? Jordan has an interesting answer. He suggests that, instead of regarding biology as a complicated, macroscopic limit of microphysics, it might be more appropriate to regard microphysics as the “simplified limit case of the organic, characterized as a minimum of the generation of integral whole,” by which he means just that the properties of macroscopic biological structures and processes commonly represent statistical averages that result from the integration of individual atomic processes. Thus biological laws may be seen, by comparison with the laws of the inorganic, as “the more comprehensive and general” (Jordan 1936a, 302).

Jordan’s Anschauliche Quantentheorie concludes with section three of chapter 5, a highly philosophical discussion of “The Construction of the Real World.” The section begins with a long quotation from Planck’s widely read 1931 essay, “Positivismus und reale Aussenwelt” (Planck 1931), in which Planck defends an unabashedly metaphysical version of realism and denounces positivism for its denial of the existence of an objective, external reality. Jordan brushes off Planck’s argument on the grounds that his notion of the real fails to pass the positivist’s test of meaningfulness. But Jordan notes that there is an interesting and empirically meaningful assertion hidden within Planck’s realism, namely, the assertion of the “univocal determination” of the physicist’s model of the world. This formulation of the realism problem, which, Jordan remarks, had already been proposed by Carnap,¹⁸ makes it into a real problem, not a pseudo-problem, for whether or not there is such univocal determination is a question that physics can answer.

Thus formulated, however, the realism question receives an affirmative answer within the framework of classical physics, but after the development of the quantum theory, it receives a definitive negative answer because of quantum indeterminism. And this is connected, in turn, with Bohr’s principle of complementarity and the role of the observer in quantum measurement, for the impossibility of organizing the results of individual acts of observation in “a single, coherent, objective model” means that the connections among the various observational results can be “only statistical” (Jordan 1936a, 309). But while the classical conception of reality is, thus, repudiated by quantum theory, the new physics is the equal of the old in “clarity and mathematical precision,” and far from this representing the end of physics, it means that research enters “newly opened realms of knowledge” (Jordan 1936a, 309).

Letting go of the classical notion of physical reality also has implications for the way we think of the relationship between the physical and the organic. Bohr had famously extended the principle of complementarity to describe the relationship between physics and biology. Beyond a certain limit, only the dead organism can be dissected and its parts studied in isolation and detail. The living organism can be studied only as an organic whole. Bohr suggested a similarly complementary relationship between physiology and psychology, and yet again, within psychology, a kind of complementarity between consciousness and its explanation, for the moment one steps back to think about one’s conscience experience or thought, that conscious experience or thought becomes something other than what it was when one was not reflecting upon it (Bohr 1933). Jordan now adds examples from the subconscious or the semi-conscious, as with the phenomenon of falling asleep. If, in introspection, one tries to observe oneself at the moment one falls asleep, then one does not fall asleep (Jordan 1936a, 313). Jordan sees in such examples additional evidence for the surmise that the development of quantum mechanics has taught us something new and important about the relationship between subject and object. What is suggested is “the blurring of the boundary between subject and object in the process of observation” (Jordan 1936a, 315). If we define the subjective “inner world” as the “private,” and the objective “outer world” as the “social,” then one comes to suspect that the two are distinguished not in kind but only in degree (Jordan 1936a, 318). And it follows that there probably are, then, intermediate states—Jordan dubs them Zwischenstufe—about which one cannot say whether they are part of reality or not. As a possible example of such a “Zwischenstufe,” Jordan suggests the telepathic communication of thoughts. It is unfortunate, on Jordan’s view, that serious scientific investigation of these phenomena has been impeded by the unjustified inclination to think them impossible on a priori grounds.

11.4 Conclusion

With good reason one might say that these last paragraphs of Jordan’s Anschauliche Quantentheorie represent the reductio ad absurdum of his larger philosophical project. But simply to dismiss the book because it ends in such silliness would be to miss the book’s larger significance. For there are two ways in which the book affords, in fact, an interesting perspective on its author and the many contexts in which the book lives.

There is, first, the fact that Jordan and his Anschauliche Quantentheorie probably did more than any other person and text to establish the association between Bohr’s interpretation of quantum mechanics and positivism. No other thinker was as central as Jordan both to the core community of quantum physicists associated with Copenhagen and to the core community of philosophers of science associated with Vienna. Nowhere else in the literature of the 1930s will one find as extensive and technically adept a presentation of the case for an essential link between quantum mechanics and positivist epistemology. Never mind the fact that Bohr, himself, never endorsed such a linkage. That this was not Bohr’s own understanding of the philosophical significance of quantum theory is of minimal relevance to our understanding how it was that the widespread, popular association of quantum mechanics and positivism was established.

There is, second, the fact that the only way to make Jordan’s odd mixing of quantum mechanics, positivism, and vitalism at all coherent is to embed the whole in the political context of Germany in the mid-1930s. For it is Jordan’s politically driven opposition to materialism that ties all of the pieces together. And therein lies a great irony. For it is Jordan, a member of the Nazi party, who in this way secured the popular association of quantum mechanics with a positivism that otherwise bore almost exclusively a left-liberal, even socialist political stamp.

Abbreviations and Archives

References

Footnotes