Chapter structure
- 3.1 Introduction
- 3.2 The origin of notation systems in Mesopotamia in the third millennium BCE
- 3.3 The problem of multiplication and of the calculation of areas of fields
- 3.4 The invention of the surveyors’ formula
- 3.5 Sophisticated surveying techniques in the Ur III period
- 3.6 From context-dependent to abstract notations of quantities
- 3.7 The heritage of the surveyors in Babylonian mathematics
- 3.8 Conclusion
- Bibliography
- Footnotes
3.1 Introduction
Knowledge about the early development of human cognition can be gained from two sources:
1Archaeologically excavated artifacts can be interpreted by elaborating the minimal cognitive preconditions that made the invention and use of these artifacts possible.
2If archaeological findings suggest that social and economic settings in an early human community are similar to those known from indigenous peoples untouched by modernization processes, it can be concluded that their members possessed similar cognitive abilities required to perform similar activities.
For the conditions under which prehistoric humans lived, abilities reconstructed by methods of this type are, as a rule, perfectly sufficient to master the problems to which they were exposed in their environment. Compared to later historic developments, however, such abilities show characteristic differences.
Max Wertheimer showed that indigenous cultures do not share our context-independent concept of number, but solve problems involving the judgement of quantities with context-specific mental constructions he called Zahlgebilde.1 Counting sequences, if there are any, remain rudimentary. They are often linked to the specific classes of objects to which they are applied. No elaborated instruments for measuring sizes are used. Consequently, the languages
The situation is similar in the case of the concepts of time and space. Norbert Elias has argued convincingly that the metric concept of time is a product of modern economy and technology and neither required nor functional in premodern societies.2 The classical concept of space, and more so the concept of space as an aspect of the integrated concept of spacetime in contemporary non-classical physics, are also dependent on conditions provided by modern science and technology. By contrast, the previous chapter has shown how tasks involving abilities of spatial orientation were solved among non-literate peoples. The development of spatial knowledge in these communities is linked closely to external knowledge representations, in particular to coordinated actions, landmarks
This raises the interesting question about the historical circumstances under which the nature of the conceptualization of space changed and what brought about these changes. Obviously, this development is somehow related to the invention of writing
The focus of the following analysis on this development will be concentrated on its early phase. The earliest sources that indicate innovations related to the conceptualization of spatial relations, in comparison to what is known from non-literate cultures, are administrative tools, in particular proto-cuneiform administrative tablets written between 3200 and 3000 BCE, which triggered the invention of writing
This development originated in the context of the bureaucratic administration which necessarily evolved together with the concentration of economic and military power in the early Mesopotamian cities and the emergence of socially stratified, centralized states in the time period from the late fourth to the late third millennium BCE. Measurement
3.2 The origin of notation systems in Mesopotamia in the third millennium BCE
Rural communities as we know them from indigenous cultures apply simple techniques of quantifying such as using the breadth of fingers or the length of the forearm to control productive activities of knitting, weaving, or braiding. Long distances
In the fourth millennium at the latest the nomadic tribes and rural communities in Mesopotamia were complemented by larger settlements and even fortified cities.5 This development was connected with unprecedented cognitive constructions. The first and foremost type of such constructions in the early phase of the development of new cognitive abilities triggered by administrative challenges was the integration of context-specific measures into comprehensive and standardized systems of measures represented by corresponding systems of symbolic notation
What is the evidence for such a cognitive development? Archeological finds from this period show that the new challenges of the situation required an extensive use of existing traditional methods to control quantities. This is indicated especially by the expansive use of certain geometrically shaped clay tokens whose functions were long unclear. Sealed spherical envelopes made of clay and containing combinations of such tokens finally made evident that the tokens were used as counters to document quantities of resources that were the subject of administrative transactions.7 Some of these envelopes bear impressed markings on their surfaces that – in view of the type of impression – can be identified as precursors of later numerical notations. At about the same time, such markings were pressed into the surface of sealed clay tablets, known as numerical tablets, the appearance of which immediately predates the invention of proto-cuneiform writing
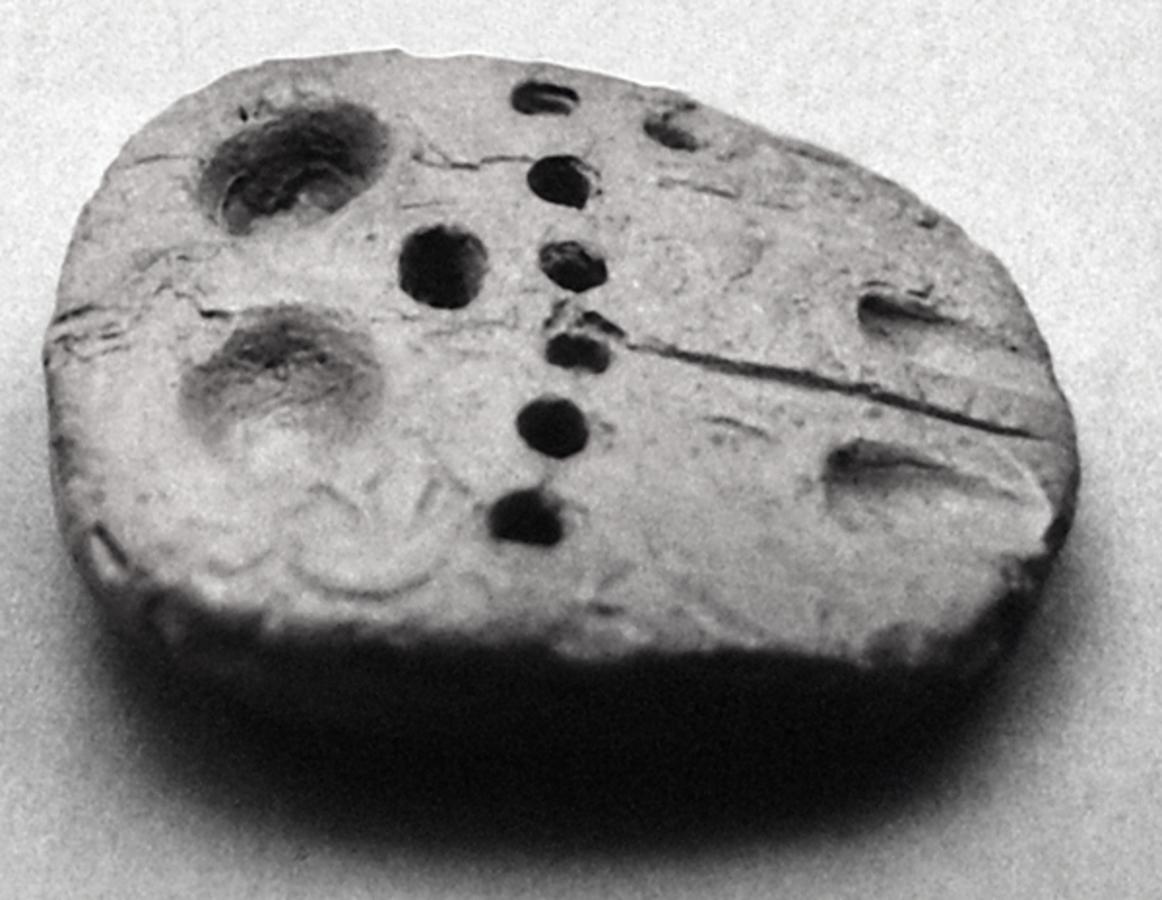
Fig. 3.1: Prehistoric sealed numerical tablet from Jebel Aruda with four series of impressions, repeated according to the quantities they represent
A close analysis of these archaeological findings and the results of deciphering the earliest proto-cuneiform administrative tablets strongly suggest that the invention of writing
Many prehistoric numerical notations preceding proto-cuneiform and cuneiform numerical notations consist of a few vertically or obliquely impressed marks similar in shape and size. They are comparable to one or more series of notches or dots as known from much older artifacts such as bones, tools, or cave paintings. It is likely that such repetitions of signs represent the quantity of the objects represented by the individual signs. Other notations on the prehistoric numerical tablets show a more complex structure. They often consist of several series of impressions that differ in size and shape. Generally, the symbols
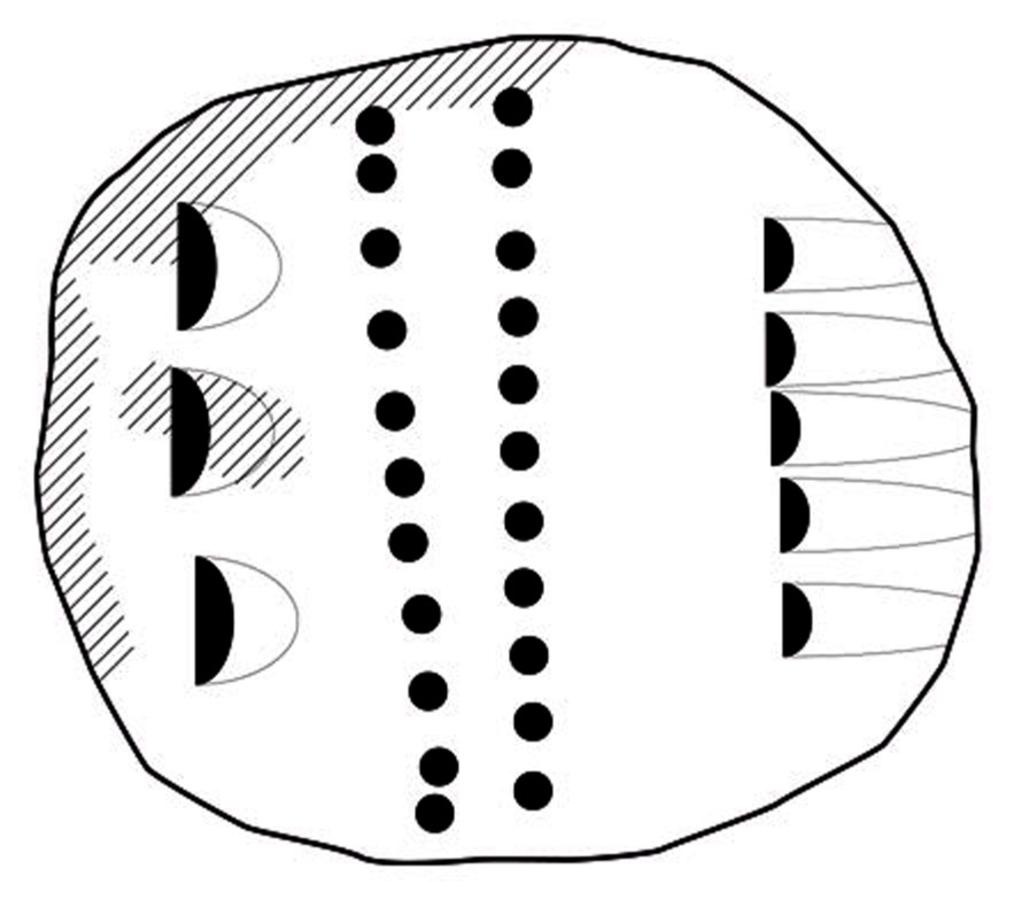
Fig. 3.2: Numerical tablet from Jebel Aruda with a sign repetition exceeding any known relation between numerical or metrological units
Without knowing the context which might explain the function of such repeated symbols
The most conspicuous properties indicating a non-numerical meaning of the individual signs are:
1The low degree of standardization of their shapes. These shapes differ from tablet to tablet. Since we do not know the context of their usage it is for the most part impossible to decide whether signs on different tablets are variants of the same sign or denote different units with different values. Their meaning seems to be determined by the context of their use rather than by internal relations within a formal system of numeration, which would it make possible to identify their meaning independent of any knowledge about the context of their use.
2Their unlimited repeatability. The numerical signs are frequently repeated more than ten times, even if they are placed in the middle of a complex numerical notation. The numerical notations of the prehistoric numerical tablets obviously lack the typical bundling structure of all known notation systems of numbers. Even when repeated small units represent an amount greater than the next higher unit, they were nevertheless not converted. This makes it at the very least likely that these symbols
These properties of prehistoric numerical notations strongly suggest that the numerical signs in fact still represent real units such as containers of different sizes, not values within a standardized system of context-independent measures. Their precise meaning was determined by the context in which they were used. This makes deciphering of the prehistoric numerical notations virtually impossible and, consequently, also the determination of the meaning of the combinations of clay tokens, which was transferred to the new medium of numerical tablets. In particular, it is impossible to find out whether prehistoric numerical notations existed which represented geometrical measures such as measures for length, area, and volume.
At the end of the fourth millennium, the situation changed radically. As a consequence of the invention of the proto-cuneiform writing
The internal consistency of the application of these rules to the numerical notations made it possible to decipher their meaning in spite of the systematic ambiguity which is a consequence of a persisting context-dependency of the meaning of the numerical signs.11
In fact, the numerical signs had no fixed numerical values. They were arranged in different, but internally coherent systems of notations with changing numerical values depending on the system in which they were used. These systems were applied consistently in specific areas of application. In order to facilitate the identification of the system, the numerical signs were partly modified by additional strokes or impressions produced with the tip of a stylus. Generally, however, the context indicated by the iconic graphs accompanying the numerical notations, and the extremely different numerical values of the signs when they were used in different systems, were sufficient to identify the notation system used. Thus, the relation of the sign representing the unit in the counting system to the next higher unit in this system changes between one to six, one to ten, and one to eighteen, depending on the context of application. The numerical signs frequently changed even the order of their numerical values. The signs with the values of 60 and 3,600 units in the counting system applied to grain measures, for example, assume the values 180 and 60 respectively. Thus the first sign, which represented
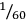 of the second sign, assumes a value 3 times higher than the second sign.12
of the second sign, assumes a value 3 times higher than the second sign.12
It is obvious that – in spite of this still existing context dependency of the numerical signs’ values on the context of their application – the consistent notation systems of the administrative proto-cuneiform tablets document a new kind of cognitive construction different from those of their prehistoric precursors. They represent the earliest well-documented notation systems of measures that are independent of the actual measuring tools, constituted by internal relations between units which determine their sizes. Among them, systems can be identified which implicitly define the dimensions
The structures of the proto-cuneiform systems of numerical notations allow for some inferences about their origins. Most of them consist of a core group of measures with numerical relations between them that lack a systematic pattern. At the upper and the lower ends, these irregular patterns tend to become systematic, based on the sexagesimal pattern of one of the two counting series also documented by the administrative proto-cuneiform tablets. This distinction within the systems suggests that the core of a notation system represents inherited prehistoric measures which in a first phase of development had to be brought into standardized numerical relations taking into account the relative sizes determined by traditional measuring tools. In a second phase the core notation system was artificially expanded in order to cover the new challenges of a central administration of goods and resources. Since such an expansion was no longer determined by existing measures, this structure could be defined much more systematically than the structure of the core of the system.
In the case of the system of length measures, the core, which consisted of measures such as the finger and the cubit, is known only from later cuneiform sources. The reason may be that these measures were unimportant for the administrative activities recorded on proto-cuneiform tablets. It seems that in the context of these activities length measures were used predominantly for surveying
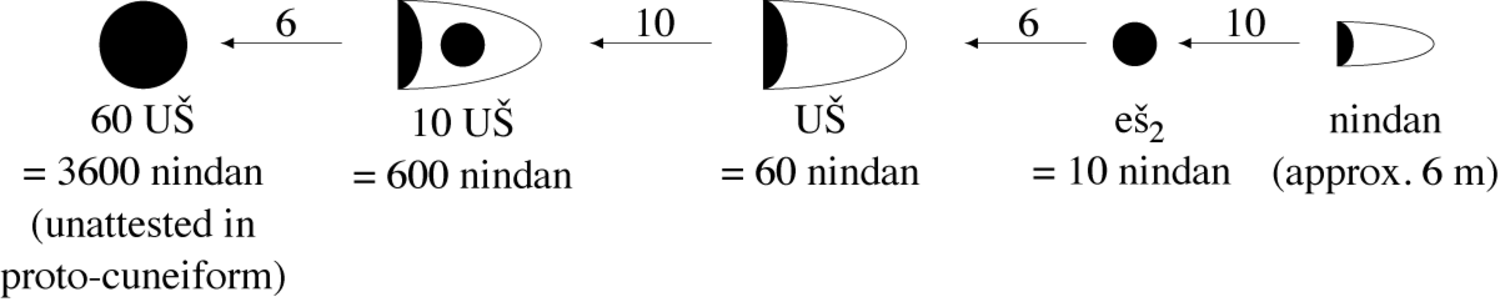
Fig. 3.3: Relations between length measures on proto-cuneiform tablets
The length measures on the administrative proto-cuneiform tablets show a strict sexagesimal structure, suggesting that they were artificially created by officials of the central administration and played no role in prehistoric times. The basis of the system was the nindan, with a size of approximately six meters, probably derived from a measuring rod

Fig. 3.4: Relations between area measures on proto-cuneiform tablets
The situation is different in the case of area measures. The core notation system starts with a unit representing a size of about 0.36 hectares or 3,600 square meters, that is, 100 times of a unit later written with the cuneiform sign sar, designating a garden.14 This basic unit of the core system of 100 sar was again written with the sign used in the sexagesimal counting system for the unit 1. It was later designated as iku, a term representing a field of arable soil. The unit iku was followed by a unit six times greater, eše3, and a unit 18 times greater, bur3. This core group of area notations was obviously derived from prehistoric measures of fields, the sizes corresponding to what one would expect from rural communities where the sizes of fields are related to the work to be invested and the yield required to support a family or a clan. With the creation of the area notation system, the measures forming the core group must have been redefined by the numbers that most closely approximate their originally imprecise relations to each other, resulting in the unsystematically organized core group of units. This core group of area notations was expanded, again following the structure of sexagesimal counting. Accordingly, the proto-cuneiform administrative tablets contain signs for 10 and 60 bur3, which were artificial extensions of the core system to meet the requirements of controlling larger areas of arable land in a stratified society as compared to rural communities.
While the notation systems of length and area measures documented by proto-cuneiform administrative tablets were dependent on each other (as will be shown in the next section), notation systems of volume measures were still completely independent at that time. The reason is that they were used in completely different contexts, probably representing containers ranging from small ration bowls up to huge silos of about 260,000 liters.15 The main area of application of this notation system was to represent amounts of different types of grain or liquid grain products. Different types of grain and grain products such as grain, barley groats, or malt were indicated by modifying the numerical signs.
The core notation system for volume measures consists of five signs with values ranging from 4.8 to 4,320 liters. Taking into account that, as a staple food, grain had to be stored for a period from one harvest to the next even in small-scale rural communities, it is plausible that all six of these measures go back to containers already used in prehistoric times. This core notation system was extended to higher units again by artificially adding sexagesimally structured signs, documented for ten and 60 times of the highest unit of the core system. The system was extended to smaller units by using unit fractions from
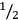 to
to
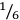 , and probably also
, and probably also
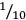 of the smallest unit of the core system.
of the smallest unit of the core system.
The creation of coherent notation systems for length, area and volume was a major step towards a context-independent concept of space. While it is true that all three systems were still closely related to certain areas of application, that is, surveying
3.3 The problem of multiplication and of the calculation of areas of fields
In addition to the creation of coherent notation systems there was another, even more influential innovation made possible by the creation of these systems. Most of these systems were constructed independently, based only on the different quantities of the same type of measure. However, in the case of length and area measures it seems that they depended on length measures from the very beginning. This connection must have influenced the construction of the notation system for areas and made it dependent on the system of length measures. This dependency probably reflects the fact that the sizes of fields were determined by surveyors
How precisely did surveyors
How were the sizes of fields calculated on the basis of these relations? From a modern point of view and assuming that the fields were rectangular their areas have to be calculated by multiplying length and width. For this purpose, the measures of length and width would have to be converted into the same unit, preferably into the smallest unit nindan. The numbers of these units would have to be multiplied by some kind of algorithm, followed by a conversion into the standard area measures. But the evidence on the extant tablets precludes this interpretation.
1The calculation of areas by multiplying the number of units of the length by the number of units of the width presupposes that the rectangular area is conceived as being covered with unit squares the number of which is defined as the size of the area. But the idea to determine the size of an area by covering it with squares was an unfamiliar idea to the whole Babylonian mathematical tradition. This is because the surveyors
2In proto-cuneiform documents the length measures were recorded with a precision down to 1 nindan. The area measures, however, were never recorded with a precision down to 1 square nindan, that is, to the level of 1 sar. While the lowest unit in area notations is usually the iku, areas are not usually recorded at this level of precision, but use iku as the smallest unit. It is unlikely that the units of sar which would automatically result from a multiplication of numbers of nindan were simply suppressed.
3The two next higher units, the eše3 with 600 sar and the bur3 with 1800 sar, can no longer be expressed as squares of a length recorded with the applied notation system. But in any case they were too big to justify the precision of 1 nindan used by the surveyors
The neglect of algorithms for performing the multiplication of arbitrary sexagesimal numbers is characteristic until the end of the third millennium. The third millennium administrative tablets document instead three different kinds of implicit multiplication already evident in proto-cuneiform administrative documents.
1Similar to the multiplication designated by the English term times, quantitative entries could be multiplied by small whole numbers, a technique which can easily be performed as repeated addition. From a modern point of view this arithmetical technique is the application of a dimensionless numeric operator to a qualified magnitude.
2Linear relations between two sets of quantities such as the numbers of workers and corresponding amounts of rations to feed them can easily be extended to tables of corresponding pairs of values by applying the first type of multiplication to both of the corresponding values. In this case the factor by which the amounts of rations could be calculated from the numbers of workers, usually a fraction, remains completely implicit. From a modern point of view this arithmetical technique is the application of a dimensionless numeric operator to a linear function.
3Areas of fields are, as we have seen, somehow calculated from length measures. From a modern point of view this arithmetical technique determines values by a bilinear function from one type of a specific kind of qualified magnitude, represented by length measures, into another type of qualified magnitude, represented by area measures.
The last type of multiplication is the subject of the discussion here. It is the only type where it is not obvious what kind of operations were performed in order to obtain the result. However, an atypical early Dynastic tablet excavated at Fara provides some critical information for the reconstruction of this procedure since it bears on its reverse some scribbled numerical notations that seem to be intermediate results of the calculation procedure.17
In the following entries on the obverse of the tablet the measures of a field and its area are registered:18
1The second entry contains its length, measuring 1 UŠ 1 eš2 2 nindan.19
2The third entry contains its width, measuring 1 UŠ 2 eš2 2 nindan.20
3The fourth entry contains an area notation of 3 bur3 5 iku. Assuming that the readings of the measures of length and width are correct, the area of the field was 3 bur3 5 iku 4 sar which is extremely close to the area of 3 bur3 5 iku registered in the fourth entry.
How was this area calculated? The answer is provided by four of the five scribbled numerical notations on the reverse of the tablet:
1The second line contains the notation 2 bur3 1 eše3 1 iku 20 sar, which is precisely the area of a field with a length of 1 UŠ 1 eš2 2 nindan and the width of 1 UŠ.
2The third line contains the notation 2 eše3 2 iku which is close to the area of a field with the same length of 1 UŠ 1 eš2 2 nindan and the width of 2 eš2.21
3The fourth line contains the notation 3 bur3 3 iku, which is the sum of the second and the third line, thus representing the area of a field with a length of 1 UŠ 1 eš2 2 nindan and a width of 1 UŠ 2 eš2. Again, the precise value of 3 bur3 3 iku 60 sar was rounded by dropping the 60 sar.
4Finally the fifth line contains the area of a field of 1
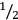 iku(?) which is the rounded value of a field with the same length of 1 UŠ 1 eš2 2 nindan and the width of 2 nindan.22
iku(?) which is the rounded value of a field with the same length of 1 UŠ 1 eš2 2 nindan and the width of 2 nindan.22
Thus three of the scribbled numerical notations on the reverse of the tablet represent the results of the calculation of partial areas of the field with a length of 1 UŠ 1 eš2 2 nindan, and the three parts of the width 1 UŠ, 2 eš2, and 2 nindan. Their sum, 3 bur3 4
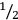 iku, is the approximate area of a field with a length measuring 1 UŠ 1 eš2 2 nindan and a width measuring 1 UŠ 1 eš2 2 nindan as registered in the second and third entry on the obverse of the tablet. Rounded up to 3 bur3 5 iku, the calculated area equals the fourth entry on the obverse of the tablet.
iku, is the approximate area of a field with a length measuring 1 UŠ 1 eš2 2 nindan and a width measuring 1 UŠ 1 eš2 2 nindan as registered in the second and third entry on the obverse of the tablet. Rounded up to 3 bur3 5 iku, the calculated area equals the fourth entry on the obverse of the tablet.
This suggests that the ancient scribes used a calculation procedure based on the knowledge of the area for each pair of units of length and width measures:
If the length equals 1 nindan and the width 1 nindan then the area equals 1 sar.
If the length equals 1 nindan and the width 1 eš2 then the area equals 10 sar.
If the length equals 1 nindan and the width 1 UŠ then the area equals 60 sar.
If the length equals 1 eš2 and the width 1 eš2 then the area equals 1 iku.
If the length equals 1 eš2 and the width 1 UŠ then the area equals 1 eše3.
If the length equals 1 UŠ and the width 1 UŠ then the area equals 2 bur3.
A field with a length or or a width that is a multiple of a length unit has an area which is the same multiple of the corresponding unit area, that is, the area grows linearly with its length or width. Thus, partial areas such as those represented by the scribbled notations on the reverse of the tablet discussed above could easily be calculated from the unit areas by using the well-documented techniques to operate with linear relations.
This procedure was necessarily specific for the calculation of areas and was never adapted to other problems that, from a modern point of view, involve multiplication. It was based only on the arithmetical techniques described above. Furthermore, it was implicitly assumed that the sum of the sizes of partial areas equals the size of the total area. Besides these conditions the procedure did not presuppose any arithmetical techniques that are unattested by the extant sources. In particular, the sizes of areas could be determined without making a detour through an intermediate sexagesimal result.
The precondition for effective application of such a procedure was, however, the knowledge of the sizes of unit areas for all combinations of length and width units. Tablets dating back to the first half of the third millennium, in fact, document that learning the sizes of such unit areas was an important part of the training of the scribes. From the Early Dynastic II period around 2700 BCE onward, school tablets survived containing tables or problems which could be calculated or solved by applying simple linear operations to the unit areas. Tables of this kind usually do not contain the unit areas directly but rather areas calculated from single-digit sizes of length and width, that is, sizes represented by multiples of a single sign.
The earliest tablet containing such a table, dates back to the Fara period.23 Three columns list, first, the length of a field, followed by its width (equal to the length) and the calculated area. The lengths and widths go down from 10 to 1 UŠ, which equals 6 eš2, continuing from 5 to 1 eš2, and ending up with 5 nindan, which is half of 1 eš2.
Such tables do not necessarily contain lengths and width with equal sizes. A recently published tablet24 is quite similar to the tablet from the Early Dynastic II period, but starts with a length of 5 nindan and a width of 5 UŠ, continuing by doubling both sizes to 1 eš2 and 10 UŠ, respectively, subsequently adding 1 eš2 and 10 UŠ to length and width, respectively. This operation goes up to 5 eš2 and 50 UŠ.25
Of special interest concerning the learning of the sizes of unit areas as a precondition for calculating areas is an Old Akkadian tablet some one hundred years younger, containing a problem and its solution.26 The problem concerns small Old Akkadian length and area measures.
The length measures used are:
| 2 zipaḫ | = 1 GIŠ.BAD (= a cubit of approx. 50 cm) |
| 2 GIŠ.BAD | = kuš3-numun |
| 6 kuš3-numun | = 1 nindan |
| 10 nindan | = 1 eš2 |
The area measures used are:
| 60 gin2-tur | = 1 gin2 (= approx. 0.6 square meter) |
| 60 gin2 | = 1 sar |
| 100 sar | = 1 iku |
The tablet contains the problem to calculate the area of a quadrilateral with equal sides the lengths of which are the sum of the involved length units. Thus, each side has the length:
1 eš2 1 nindan 1 kuš3-numun 1 GIŠ.BAD 1 zipaḫ
If, in fact, the calculation method was based on the knowledge of the unit areas, this seemingly strange problem finds a simple explanation: The solution of the problem requires adding up the 25 unit areas, each combining two length units. With this problem the teacher therefore was able to check whether his pupils knew these unit areas or were able to calculate them.
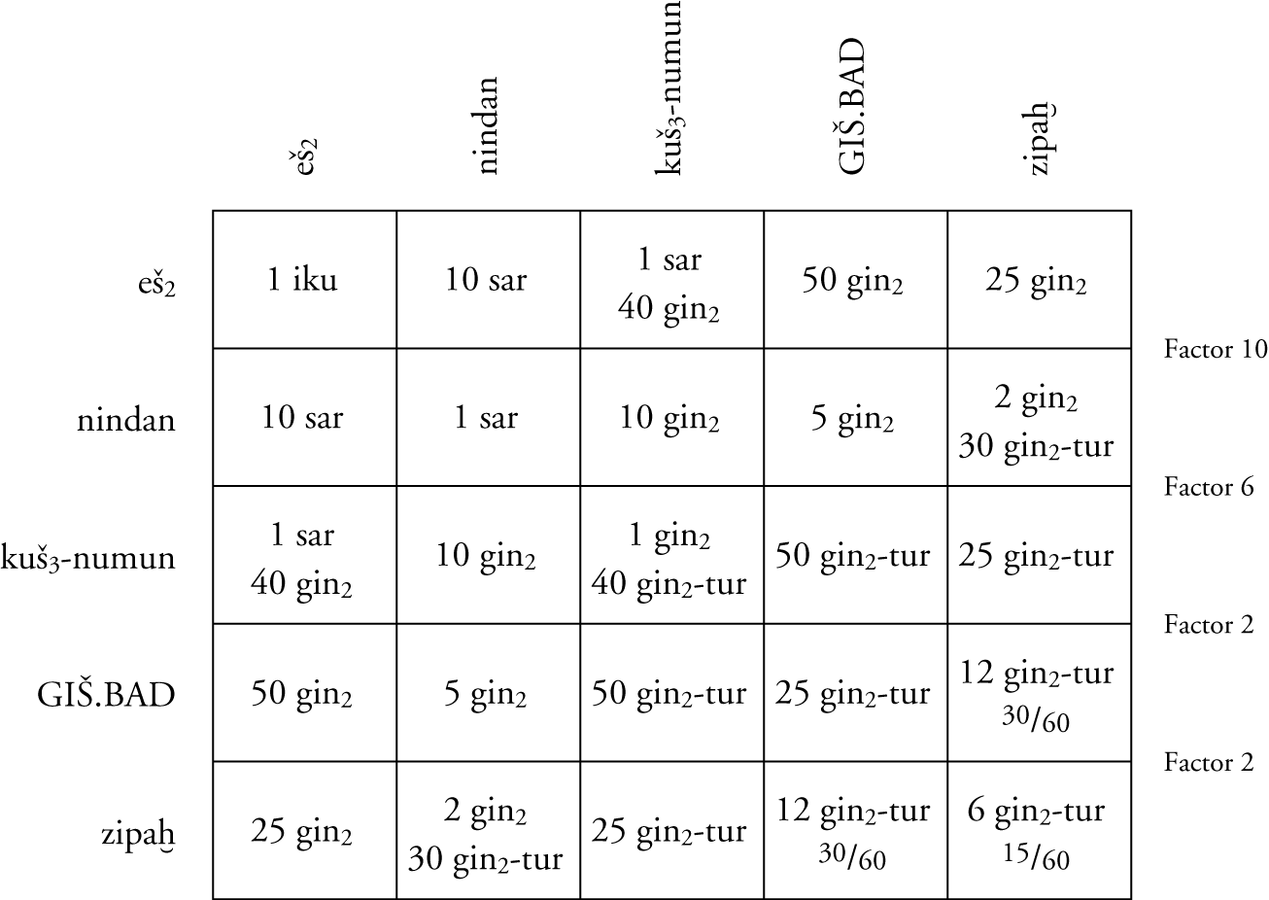
Fig. 3.5: Unit areas that had to be known to solve the problem on an Old Akkadian school text (Limet 36)
This procedure remained difficult to perform, however. In the third millennium, tablets containing length and area measures often show errors in the calculation of the areas, and partial areas including small measures were often treated negligently. Thus, in this case as well, the given solution is not correct.
The tablet contains the solution:
11/4 (iku) gan2 21/2 šar 6 gin2 15 gin2-tur
The correct solution would have been:
11/4 (iku) gan2 21/2 šar 6 gin2-tur 15/60 gin2-tur
The cause of the error is obvious.27 The smallest unit area has the size:
6 gin2-tur 15/60 gin2-tur
It was erroneously interpreted as:
6 gin2 15 gin2-tur
Given that no designation is known for
1/60
of the small unit gin2-tur (about 1 square decimeter) the error may well have been caused by the scribe’s unfamiliarity with such small units, which, in fact, played no role in the contemporary practice of surveying
3.4 The invention of the surveyors’ formula
The determination of the size of an area from its measured length and width met only some of the challenges with which the surveyors of the administration of the early states were confronted. The fields they had to measure were rarely regular enough that their sizes could be determined on the basis of just measuring a length and a width. They usually were quadrilaterals with four unequal sides.
In order to solve the problem to calculate the size of such fields, the surveyors of the third millennium Mesopotamia already used what is called the surveyors’ formula.
This formula is well-known, in particular from later Greek and Roman surveying technology
Determining the mean of two measures was a simple problem given the notation of measures used by the ancient scribes of Mesopotamia. As a rule, the opposite sides of a field did not differ too much so that the number of higher units of the notation of their sizes was equal. These units could simply be neglected. Only the differing parts of lower units had to be added for each pair, and then half the result had to be appended to the strings of higher units in order to get an area with equal opposite sides.
This procedure is well documented by sources from the second half of the third millennium. However, a favorable circumstance allows us to trace the roots of this formula back to the end of the fourth millennium, that is, to the origins of cuneiform writing
There are several indications that the tablet contains a school text:
1The text contains an exercise, giving the primary data, but not the solution.
2The field area to be calculated is unrealistically large, corresponding to an area of a field with a length of about 7 km and a width of about 5 km. At the beginning of the third millennium, such a huge field would not fit into what is known about sizes of individual fields at that time. Numerical area notations of this order of magnitude occur only as totals of several fields.
3The solution would have to be written with a sign for 10 šar
In addition to the attestation of the earliest known use of the surveyors’ formula, the tablet provides further important information. Starting from a predetermined result, the exercises are constructed accordingly on both sides of the tablet to produce the desired result. In the present case, the desired result is 10 šar
This exercise tablet thus throws some light on the origins of the surveyors’ formula. The ancient surveyors apparently assumed that the area of a field remains equal if they subtract some part from one side of a field and add a part of the same size to the opposite side.
From a modern point of view, the surveyors’ formula yields only an approximate value of the ‘real’ area, that is, the procedure approximates the area as it is defined in the tradition of Euclidean geometry
Moreover, for the time before the first millennium BCE there are no indications of any alternative concept of area that might have taken into account not only length measures but also the angles
3.5 Sophisticated surveying techniques in the Ur III period
The second half of the third millennium BCE was the era of the rise of big empires in Mesopotamia, culminating in the empire of the Third Dynasty of Ur (known as the Ur III period) which integrated southern and northern Mesopotamia and even parts of southwestern Iran for somewhat less than 100 years.28 This integration was accompanied by reforms in the techniques of social control initiated by the powerful emperor Šulgi and, in particular, in the bookkeeping techniques used by the centralized administration.
One of these innovations concerned the administration of arable land. Šulgi created a new category of royal domains that were distributed to high-ranking officials in exchange for their services. Fields such as those of the royal domains could take on considerable size and an irregular shape.
This may be the reason for the emergence of a new type of cuneiform tablets documenting the work of surveyors. These documents do not simply give the measures of the surveyed fields but also drawings
Fig. 3.6: Field map of the Ur III period (MVN 10, 214)
Triangles were considered to be half of a quadrilateral with the longest side as the common side of both halves. Accordingly, the size of their area was calculated by halving the product of their two smaller sides. The size of the area of quadrilaterals was calculated using the surveyors’ formula. In this way, first the size of the temen was calculated by adding up the partial areas in the case of complex shapes of the temen. The measuring and calculation of the sizes of the small appended or cut-off areas was often simplified by measuring only three of the four sides of a quadrilateral, leaving out the measurement of the outer border. The results of the calculation of the sizes of the appended or cut-off areas were then added to, or subtracted from, the size of the area of the temen in order to obtain the size of the total area of the irregularly shaped field.
It is characteristic of the field maps
3.6 From context-dependent to abstract notations of quantities
Besides the use of maps to document complex shapes of fields and to organize the calculation of their areas, the Ur III period with its centralized administration provided the setting for what can be considered the most important mathematical invention of the ancient Near East, that is, the invention of the sexagesimal positional system
Before the Ur III period numerical notations were based without exception on signs or sign combinations representing the absolute value of metrological units or, in the case of counting, on specific signs for each base unit, that is, specific signs for 1, 10, 60, 600, 3600 etc. The innovation consisted in repeating the signs for 1 and 10 for the higher units, that is, using 1, 10, 1, 10, 1 etc. for the same sequence of units, distinguishing them only by their position. Eleanor Robson characterized this innovation by arguing that the sexagesimal place value system
... changed the status of numbers from properties of real-world objects to independent entities that could be manipulated without regard to absolute value or metrological system.30
Although the missing zero and the missing separation between whole units and fractions (comparable to the decimal comma in the modern decimal positional system) caused difficulties in applying the new system, the purpose of the innovation is clear and its inherent potential is obvious. Its invention was a precondition for the development of efficient calculation methods, in particular of universally applicable algorithms for multiplication and division
Unfortunately, the origin of the new system is difficult to trace. For a long time the question was simply neglected, assuming that dealing with quantities is in any case a universal
This situation changed over the last decades, along with a growing interest in texts of the third millennium that somehow indicate mathematical knowledge, but do not belong to the corpus of Babylonian mathematics in the narrow sense as it was understood by the pioneers of the decipherment of mathematical cuneiform texts, in particular Otto Neugebauer and Françoise Thureau-Dangin.31 In this context the search for the earliest attestations of numerical notations written
In contrast to the high number of cuneiform tablets documenting the use of the sexagesimal positional system
However, the inherent potential of the sexagesimal positional system
The abundance of extant early second millennium tablets dedicated to the use of the new system shows unambiguously that this potential was in fact realized shortly after its invention. The majority of these tablets contain tables which were probably produced in the context of scribal schools to teach them to perform the operations of the new system. A brief survey of the most frequent types of such tables elucidates how systematically the potentials of the new system were explored and transformed into techniques to handle quantitative data:34
1Metrological tables containing lists of traditional metrological notations, in particular notations of capacity measures, weight measures, length measures, and area measures, ordered according to the sizes of the values they represent in the first column, and corresponding notations in the new sexagesimal positional system
2Multiplication tables containing the multiples 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 30, 40, 50, and 60 of certain fixed numbers, for example 6: 1 times 6, 2 times 6, etc.
3Tables of reciprocals containing, as a rule, the reciprocals of 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, 40, 45, 48, 50, 54, 60, 1 4 (= 60 + 4 = 64), and 1 21 (= 60 + 21 = 81).
4Tables of coefficients used for converting values such as, in the context of architecture, to convert a volume into the number of bricks required to fill it; in the context of metal work to convert an area to be gold-plated into the required amount of gold; in the context of geometry to convert the length of the side of a square into its diagonal.35
This enormous corpus of hundreds of tablets from the short period of approximately 500 years after the invention of the sexagesimal positional system
1The Metrological tables document the basic continuity between the traditional metrological systems and the sexagesimal positional system
2The Multiplication tables were created using the method familiar from treating linear relations between two sets of quantities by applying repeated additions to both sets.
3The Tables of reciprocals were created by using and further developing a technique that had been developed in the context of the strictly sexagesimally structured weight measures to replace unit fractions such as
 ,
,
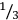 ,
,
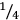 ,
,
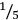 , etc., with a combination of multiples of smaller units, that is, 30, 20, 15, 12, etc. units.36
, etc., with a combination of multiples of smaller units, that is, 30, 20, 15, 12, etc. units.36
4The Tables of coefficients make the implicite factors of linear relations explicite. These tables show that the invention of the sexagesimal positional system
The extent to which the sexagesimal positional system
There are further differences from the modern decimal positional system. First, the sexagesimal positional system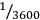 ,
,
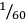 , 60, 602, 603, etc. Thus, additions and subtractions required an independent control of the absolute sizes. Second, the system lacked a sign for zero so that notations that required an inner zero became ambiguous.
, 60, 602, 603, etc. Thus, additions and subtractions required an independent control of the absolute sizes. Second, the system lacked a sign for zero so that notations that required an inner zero became ambiguous.
Division
In spite of the integration of metrological notations into a closed system of abstract numerical operations, this system evidently differs from the modern number concept. It is, in fact, difficult to imagine how, long before the creation of modern mathematical formalism, a numerical system without an inherent absolute value of its entities could be conceived. In fact, neither in the Sumerian
The conceptual change from metrological to sexagesimal positional
3.7 The heritage of the surveyors in Babylonian mathematics
The types of knowledge discussed so far were more or less forms of the knowledge of practitioners. It is characteristic of such knowledge that it is determined by the goals of its practical use. These goals limit the range of applications and at the same time the potential for further developments. However, social institutions
This new type of knowledge transmission changed the character of the knowledge itself. Knowledge transmitted by institutionalized
1The texts were neither signed by a responsible official nor dated.
2The scope of the exercises was unrealistically extended beyond any practical needs.
3The values of exercises were systematically varied and often documented in the form of tables representing relations between conditions and results, for instance, tables of length measures together with the calculated areas.
4Conditions and results of administrative procedures were exchanged in order to produce new types of exercises: Results of typical operations of practitioners such as a calculated area together with, for instance, the length of a field were given from which the width had to be calculated.
While the operations with traditional metrological notations were not substantially influenced by school traditions, the impact on operations with the sexagesimal positional system
1The area and the side of a square I have added: 45 is it.
2The side of a square I have subtracted from its area: 14 30 is it.
3The third of the area of a square I have subtracted. The third of its side I have added: 20 is it.
4The third of the area of a square I have subtracted. The side I have added: 4 46 40 is it.
In all four problems, the task is, of course, to determine the length of the side. Keeping in mind that the notations in the sexagesimal positional system
130 times 30 is 15 (times 60). 15 plus 30 is 45 (the given area).
230 times 30 is 15 (times 60). 15 (times 60) minus 30 is 14 30 (the given area).
330 times 30 is 15 (times 60). The third of 15 is 5. 15, the area, minus 5 is 10. The third of 30, the side, is 10. 10 plus 10 are 20 (the given area).
420 times 20 is 6 40 (6 times 60 plus 40). The third of 6 40 is 2 13 20 (times
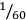 ). 6 40, the area, minus 2 13 20 (times
). 6 40, the area, minus 2 13 20 (times
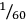 ) is 4 26 40 (times
) is 4 26 40 (times
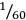 ). 4 26 40 (times
). 4 26 40 (times
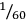 ) plus 20, the side, is 4 46 40 (times
) plus 20, the side, is 4 46 40 (times
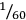 , the given area).
, the given area).
While the arithmetical operations of multiplication and division
This common-sense interpretation is supported to a certain degree by recent philological work.42 It turns out that the concepts represented by the terms used are partly arithmetical and partly geometrical, representing the traditional distinction between different kinds of metrologically determined operations, in particular different kinds of multiplication.43 Thus, in the present example the term for multiplication is identical with the term for the area of a field, the terms for addition and subtraction seem to have an arithmetical origin, even though the values to which they are applied, the sizes of lengths and areas, also have a clear geometrical meaning. It is therefore plausible, that the ancient scribes kept track of the absolute values of the arithmetical notations by keeping in mind their metrological meanings.
In contrast to the simplicity of problems based on the operations of the practitioners, reverse operations led to more sophisticated problem solutions. Albeit recorded on many of the tablets, they are still poorly understood.44 In modern terms, the examples given above represent second-degree equations:
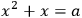
|
3.1 |
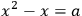
|
3.2 |
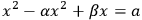
|
3.3 |
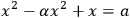
|
3.4 |
Solutions to such problems, if featured on the tablets, describe only the operations to be performed with the given sexagesimal positional
The new geometric interpretation of key terms of Babylonian mathematics undermined this understanding. For the first time, some Babylonian problem solutions, at least, became plausible on the basis of hypothetical geometrical figures, which might have existed on scrap pads or as memorized mental images.
As a consequence of this geometric turn in the interpretation of problems posed in Babylonian mathematics, there is a tendency to supplement them systematically with Euclidean-style figures. Given that there is a common basis of practitioners’ knowledge in Babylonian and Euclidean geometry
The geometrical problems of Babylonian mathematics were determined by
1the length of straight lines, which may approximate curved lines,
2the assumption that the size of a figure which consists of partial areas equals the sum of these partial areas,
3the assumption that the area of a quadrilateral is determined by the surveyors’ formula
With the Euclidean concept in mind, these assumptions could lead to counterintuitive consequences. On one of the Old Babylonian mathematical tablets,47 for instance, a quadrilateral is cut into two equal pieces. The scribe asked for the length of the dividing line.
From a Euclidean perspective
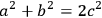
|
3.5 |
This example is not an exceptional one but rather the simplest kind on a type of tablets that deal with the division
From the origin of writing
But is it possible that this was also the perspective of the Babylonian scribes? There is, in fact, no evidence whatsoever that they considered their calculation of areas to be some kind of approximation of a different understanding of ‘true’ areas for which they had neither a theoretical nor even a conceptual basis. While they probably were aware of the fact that their calculated areas were not precise in any absolute sense, they surely did not see any difference between the dependence of area measures on external circumstances and the limited precision of measures such as the measures of lengths, weights, volumes, or economic exchange rates. But there were, of course, practitioners’ rules of thumb for achieving reproducible results, such as checking the reliability of a balance in equilibrium by exchanging the sides of the load and the balance weight, or applying the surveyors’ formula
The scribes who composed Babylonian mathematics inherited this understanding of area measures from the surveyors
3.8 Conclusion
This chapter investigated the development of abilities to deal with spatial relations in ancient Mesopotamia.49 It covers the time period from pre-history in the fourth millennium BCE to the first half of the second millennium BCE when Babylonian mathematics reached its first climax. At the beginning of the chapter the questions were posed as to the historical circumstances under which the nature of the conceptualization of space changed from spatial orientation techniques in pre-historic times to Babylonian geometry
Summarizing the results of the chapter, two major innovations can be identified that triggered fundamental changes related to spatial cognition. Both innovations concern the representation of spatial relations by notation systems. The first innovation was closely related to the transition from rural communities in the alluvial plane of Mesopotamia to the centralized and stratified societies of the first city states. This transition was associated with the development of administrative tools such as seals, tokens, numerical impressions into clay, and finally the invention of the proto-cuneiform writing
The overall development of knowledge which had its origin in the practitioners’ knowledge of surveyors
Bibliography
Alt, Robert (1956). Vorlesungen über die Erziehung auf frühen Stufen der Menschheitsentwicklung. Berlin: Volk und Wissen.
Bauer, Josef, Robert K. Englund, and Manfred Krebernik (1998). Mesopotamien: Späturuk-Zeit und Frühdynastische Zeit. Annäherungen 1. Göttingen: Vandenhoeck & Ruprecht.
Boltz, William G. (2006). Pictographic Myths. In: Sprache und Denken in China und Japan. Ed. by Wolfgang Behr and Heiner Roetz. 30. Bochum Yearbook of East Asian Studies (BJOAF). Bochum: Faculty of East Asian Studies at Ruhr-Universität Bochum, 39–54.
Bruins, E. M. (1955). On the System of Babylonian Geometry. Sumer 11(1):44–49.
Damerow, Peter (2001). Kannten die Babylonier den Satz des Pythagoras? Epistemologische Anmerkungen zur Natur der Babylonischen Mathematik. In: Changing Views on Ancient Near Eastern Mathematics. Ed. by Jens Høyrup and Peter Damerow. Berlin: Reimer, 219–310.
Damerow, Peter and Robert K. Englund (1987). Die Zahlzeichensysteme der Archaischen Texte aus Uruk. In: Zeichenliste der Archaischen Texte aus Uruk (ATU 2). Ed. by Margret W. Green and Hans J. Nissen. 2. Archaische Texte aus Uruk. Berlin: Gebr. Mann, 117–166.
Deimel, Anton (1923). Schultexte aus Fara. Die Inschriften von Fara. Leipzig: Hinrichs.
Driel, G. van (1982). Tablets from Jebel Aruda. In: Zikir Sumin. Ed. by G. Van Driel. Leiden: Brill, 12–25.
Dunham, Sally (1986). Sumerian Words for Foundation. Revue d'Assyriologie 80:31–63.
Edzard, Dietz O. (1969). Eine altsumerische Rechentafel. In: Lisan mithurti: Festschrift Wolfram Freiherr von Soden. Ed. by Wolfgang Röllig. Kevelaer: Butzon und Bercker.
Elias, Norbert (1984). Über die Zeit. Frankfurt a. M.: Suhrkamp.
Friberg, Jöran (1981). Methods and Traditions of Babylonian Mathematics: Plimpton 322, Pythagorean Triples, and the Babylonian Triangle Parameter Equations. Historia Mathematica 8:277–318.
– (2005a). On the Alleged Counting with Sexagesimal Place Value Numbers in Mathematical Cuneiform Texts from the Third Millennium BC. Cuneiform Digital Library Journal 2005:2.
– (2005b). Unexpected Links between Egptian and Babylonian Mathematics. New Jersey: World Scientific.
– (2007a). A Remarkable Collection of Babylonian Mathematical Texts. New York: Springer.
– (2007b). Amazing Traces of a Babylonian Origin in Greek Mathematics. New Jersey: World Scientific.
Fuÿe, Allotte de la (1915). Un cadastre de Djokha. Revue d'Assyriologie 12(1):47–54.
Gandz, Solomon (1929). The Origin of Angle-Geometry. ISIS 12(1929):452–481.
Gibson, McGuire and Robert D. Biggs (1991). The Organization of Power: Aspects of Bureaucracy in the Ancient Near East. 2nd ed. Chicago: The Oriental Institute of the University of Chicago.
Hilprecht, H. V. (1906). Mathematical, Metrological and Chronological Tablets from the Temple Library of Nippur. Philadelphia: Department of Archaeology, University of Pennsylvania.
Høyrup, Jens (1990). Algebra and Naive Geometry. Altorientalische Forschungen 17:27–69, 262–354.
– (2002). Length, Width, Surfaces: A Portrait of Old Babylonian Mathematics and Its Kins. New York: Springer.
Høyrup, Jens and Peter Damerow, eds. (2001). Changings Views on Ancient Near Eastern Mathematics. Berliner Beiträge zum vorderen Orient. Berlin: Reimer.
Hyman, Malcom D. (2006). Of Glyphs and Glottography. Language and Communication 26(3-4):231–249.
Jestin, R. (1937). Tablettes sumérienne de Shuruppak conservées au Musée se Stamboul. Paris: Boccard.
Limet, Henri (1973). Étude de documents de la periode d'Agade appartenant à l'Université de Liège. Bibliothèque de la Faculté de Philosophie et Lettres de l'Université de Liège. Paris: Société d'Editions « Les Belles Lettres ».
Neugebauer, Otto (1935/1937). Mathematische Keilschrifttexte. Berlin: Springer.
Neugebauer, Otto and Abraham Sachs (1945). Mathematical Cuneiform Texts. New Haven: American Oriental Society.
Nissen, Hans Jörg, Peter Damerow, and Robert K. Englund (1993). Archaic Bookkeeping: Early Writing and Techniques of Economic Administration in the Ancient Near East. Chicago: Chicago University Press.
Powell, Marvin A. (1976). The Antecedents of Old Babylonian Place Notation and the Early History of Babylonian Mathematics. Historia Mathematica 3:417–439.
Proust, Christine (2008). Tablettes mathématiques de la collection Hilprecht. Wiesbaden: Harrassowitz.
Robson, Eleanor (1999). Mesopotamian Mathematics, 2100-1600 BC. Technical Constants in Bureaucracy and Education. Oxford: Oxford University Press.
– (2001). Neither Sherlock Holmes nor Babylon. A Reassessment of Plimpton 322. Historia Mathematica 28:167–206.
– (2008). Mathematics in Ancient Iraq. A Social History. Princeton: Princeton University Press.
Sachs, Abraham (1947). Babylonian Mathematical Texts I. Reciprocals of Regular Sexagesimal Numbers. Journal of Cuneiform Studies 1(3):219–240.
Schmandt-Besserat, Denise (1992). Before Writing. Austin: University of Texas Press.
Schmidt, Olaf (1980). On Plimpton 322. Pythagorean Numbers in Babylonian Mathematics. Centaurus 24:4–13.
Sjöberg, Ake W. (1973). Der Vater und sein missratener Sohn. Journal of Cuneiform Studies 25:105–169.
– (1975). Der Examenstext A. Zeitschrift für Assyriologie 64:137–177.
Strommenger, Eva (1980). Habuba Kabira, eine Stadt vor 5000 Jahren. Mainz: Zabern.
Thureau-Dangin, Françoise (1938). Textes mathématiques babyloniens. Leiden: Brill.
Vogel, Kurt (1959). Vorgriechische Mathematik, Teil II: Die Mathematik der Babylonier. Hannover: Schroedel.
Wertheimer, Max (1925). Über das Denken der Naturvölker: Zahlen und Zahlgebilde. In: Drei Abhandlungen zur Gestalttheorie. Ed. by Max Wertheimer. Erlangen: Verlag der philosophischen Akademie, 106–163.
Footnotes
The term glottographic denotes the dependence on spoken language. For a detailed discussion of the classification of early writing systems and their relation to spoken language (phonology, linearity, etc.), see Hyman 2006.
The present paper is heavily based on my inaugural lecture 1994 at the University of Konstanz and its extended publication (Damerow 2001).
For an example, see the excavation of Habuba Kabira (Strommenger 1980).
For an example see the numerical tablets of Jebel Aruda written in the second half of the fourth millennium BCE (Driel 1982).
This is true, for instance, for several of the above mentioned numerical tablets from Jebel Aruda, published by Driel 1982.
Usually called ideograms. On the precise meaning of the term iconic graph, see Boltz 2006. Later, when the cuneiform writing system had developed into writing in the proper sense, that is, a system representing spoken language, such ideograms developed into a non-syllabic notation within a syllabic writing system. The same signs are then rightly called logograms or Sumerograms (i.e., adapted from Sumerian writing).
For the results of deciphering of the proto-cuneiform numerical systems and an overview of the limited results of earlier attempts, see Damerow and Englund 1987. For a comprehensive account of the social context, see Nissen et.al. 1993 and the part written by R. Englund in Bauer et.al. 1998, 15–233.
See the overview of proto-cuneiform sign systems in Nissen et.al. 1993, 28–29.
The number of proto-cuneiform tablets documenting length measures is relatively small. They contain length measures of fields up to approximately seven kilometers. See, for example, the school text discussed in Nissen et.al. 1993, 50.
There is one tablet containing a sign possibly representing ten sar; see Nissen et.al. 1993, 57.
On the determination of the absolute sizes of the signs for capacity measures, see Damerow and Englund 1987, 153–154.
See the interpretation of this tablet in Damerow 2001, 260–261. A rough drawing of the tablet was published by Jestin 1937, TSŠ 51. According to a photo and an unpublished copy of the tablet by Kazuya Maekawa discussed by Jöran Friberg at the Third Workshop on Concept Development in Babylonian Mathematics in December 1985 in Berlin, the drawing Jestin published contains serious errors. In particular, this drawing does not distinguish between a numerical sign written at the left edge of the tablet and the scribbled notation on the reverse nearby. The reconstruction of the numerical notations presented here is based on the photo of the tablet and Maekawa’s copy.
Since the first and the last entry on the obverse and the first line on the reverse are unrelated to the calculations discussed in the following, they are not taken into account here. The first entry on the obverse which is nearly illegible, probably due to an erasure by the ancient scribe, seems to contain an area notation of 1 eše3 3 iku. This area equals the notation in the clearly legible first line on the reverse. The relation to the rest of the tablet is unclear. The colophon in the last entry of the obverse seems to contain a geographical designation and a title.
The value seems to have been corrected by the ancient scribe from 1 UŠ 2 eš2 2 nindan to 1 UŠ 1 eš2 2 nindan.
In addition to the metrological notation of the width and the sign for the width of a field, the entry contains three oblique strokes which might be interpreted as representing three units of smaller measure. Since such a small length measure does not occur on any other tablet related to surveying from the Fara period, the meaning of the three strokes remains obscure. Smaller units known from later times have various sizes. 1 nindan equals 4 ni-kaš, 6 kuš-numun, or 12 kuš, see for instance the tables of calculated areas on the tablets OIP 14, 70 Edzard 1969 and CUNES 50-08-001 Friberg 2007a, 419–425, 499–500. For all three units the additional area (between 18 and 54 sar) the additional area would not substantially change the result but bring it closer to the total area recorded in the fourth entry of the obverse.
The precise value would have been 2 eše3 2 iku 40 sar. The 40 sar have obviously been dropped.
The precise value would have been 1 iku 42 sar.
The tablet VAT 12593 was originally published by Deimel 1923 and has been discussed several times in the literature, see e.g. Powell 1976, 429–431, Nissen et.al. 1993, 136–139, Damerow 2001, 262–263, Friberg 2007a, 149–150.
Tablet MS 3047 of the Schøyen Collection, published by Friberg 2007a, 150–153, 484.
This is followed by an entry with huge sizes that are difficult to interpret.
Powell 1976, 427 has argued that the error proves that, in spite of the lack of any direct textual evidence, the principles of the sexagesimal positional system were already used in the early third millennium. Friberg 2005a, § 4.3 argued convincingly that other interpretations of the cause of the error are possible. He gives an geometrical reason different from the interpretation favored here.
According to the figures given on the field map MVN 10, 214, presented here as an example, the large quadrilateral in the center of the tablet has a length of 170 nindan (= 2 UŠ 50 nindan, written along the left side), an upper width of 53
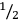 nindan (= 10 + 20 + 23
nindan (= 10 + 20 + 23
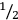 nindan, written along the upper side), and a lower width of 60 nindan (= 50 + 10 nindan, written along the lower side). If the map were drawn to scale it should thus be approximately 3 times as long as it is wide. But the drawing on the tablet is close to a square. The reverse of the tablet (not depicted here) lists the essential figures required by the administration in three lines. The first line contains the sum of the small areas to be added to the large quadrilateral. Accordingly, the third line contains the sum of the areas to be subtracted. For some reason, the area to be subtracted consists of the whole right part of the large quadrilateral (damaged soil?) and the small triangle at its upper left corner. The second line contains the remaining area of the large quadrilateral, designated as core temen. The fourth line contains the name of the field, a fifth line the name of the official who authorized the document. The interpretation of the figures in the first three lines differs slightly from the figures given on the map, but comes close enough to them not to exceed the typical lack of accuracy frequently found in surveying documents. For details on the tablet discussed here, see Gibson and Biggs 1991.
nindan, written along the upper side), and a lower width of 60 nindan (= 50 + 10 nindan, written along the lower side). If the map were drawn to scale it should thus be approximately 3 times as long as it is wide. But the drawing on the tablet is close to a square. The reverse of the tablet (not depicted here) lists the essential figures required by the administration in three lines. The first line contains the sum of the small areas to be added to the large quadrilateral. Accordingly, the third line contains the sum of the areas to be subtracted. For some reason, the area to be subtracted consists of the whole right part of the large quadrilateral (damaged soil?) and the small triangle at its upper left corner. The second line contains the remaining area of the large quadrilateral, designated as core temen. The fourth line contains the name of the field, a fifth line the name of the official who authorized the document. The interpretation of the figures in the first three lines differs slightly from the figures given on the map, but comes close enough to them not to exceed the typical lack of accuracy frequently found in surveying documents. For details on the tablet discussed here, see Gibson and Biggs 1991.
See the tables documented by Robson 2008, 81–83 and by Oelsner in his contribution to Høyrup, Jens and Peter Damerow 2001, 53–59.
Comprehensive lists and editions of such tables are supplied by Hilprecht 1906, 57–70 and Plate 1–30, Neugebauer 1935/1937, Vol. 1, 4–82, Neugebauer and Sachs 1945, 11–36, Robson 1999, 193–207, and Proust 2008, 15–73.
There are further types of tables which are, however, less common. Such tables contain, for example, squares and square roots, cubes and cube roots, exponentials and logarithms, and, to mention a unique finding, columns of figures based on Pythagorean numbers, that is, whole numbers a, b, and c that satisfy the condition
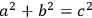 . On the various, partly incompatible interpretations of this extraordinary tablet (Plimpton 322) see Neugebauer and Sachs 1945, 38–41, Schmidt 1980, Friberg 1981, Damerow 2001, 231–232 and 294, and Robson 2001.
. On the various, partly incompatible interpretations of this extraordinary tablet (Plimpton 322) see Neugebauer and Sachs 1945, 38–41, Schmidt 1980, Friberg 1981, Damerow 2001, 231–232 and 294, and Robson 2001.
Since this method fails if the denominator has prime factors other than two, three, and five, which are the only ones contained in the base sixty of the system, such values are simply omitted in the tables of reciprocals. Furthermore, the calculation of reciprocals of notations with several digits is much more complicated. See Sachs 1947.
Two, three, and five have the reciprocals 30, 20, and 12 respectively. The prime factorization of any number containing only these prime factors has a reciprocal which is the product of the corresponding reciprocals. No other prime number has a finite representation by units of the sexagesimal system. Thus, any number containing a prime factor other than two, three, and five also has no finite representation in this system.
Frequently the Sumerian word ‘šid’ with the Akkadian translation ‘minûtu’ or the Akkadian word ‘mānu’ are considered as candidates for representing the term ‘number’. This attribution is, however, an anachronistic projection of modern concepts, neglecting the contexts in which the terms were used, as they usually related to operations and not to entities.
BM 13901, see Neugebauer 1935/1937, Vol. 3, 1–14.
Several or even the majority of historians of science will probably not agree with this statement. Translated in terms of modern mathematics most of the problems are in fact understandable. The solutions appear to be either correct or somehow flawed, allegedly due to an insufficient qualification of the ancient scribes. From the viewpoint of historical epistemology, however, such errors shed some light on the inherent mental operations of Babylonian mathematics. In spite of the progress made in the interpretation of Babylonian mathematics after the geometric turn, the present understanding of this ‘non-Euclidean’ kind of mathematics is deficient since there is still no comprehensive reconstruction of the mental models and operations that provide a coherent image of the partly successful and partly erroneous solutions of the problems documented on the tablets of Babylonian mathematics. For a critical reassessment of some interpretations of tablets allegedly dealing with the Pythagorean theorem see Damerow 2001.
Høyrup 2002, 228 discussing the role of angles and of similarity justifies the use of Euclidean-style figures:
Exactly how it [i.e. the right angle] was understood we do not know – the texts speak too little about it to allow us to understand – but it is beyond doubt that a (probably intuitive) concept of similarity or ‘same shape’ was at hand.
See for instance the tablet Strssbg. 364 Neugebauer 1935/1937, volume 1, 248–356 and volume 3, plate 11. See also the overview of similar problems provided by Friberg 2007b, 244–268. Friberg 2005b, 46–50 has convincingly shown that Egyptian mathematics dealt with problems such as those on Strssbg. 364 in the same way.
YBC 4675, published by Neugebauer and Sachs 1945, 44–48.
For a simple proof see Bruins 1955, 46 and Vogel 1959, 70.
Peter Damerow passed away before he could finish this concluding section, which he had headed “Mental models of spatial relations in the third millennium BCE.” We have not attempted to complete the section. – MS.
