After chemistry and electricity, heat
Specific and Latent Heats
Heat was a difficult field. The chemist and physician Adair Crawford
At about the same time that Cavendish carried out his first dated chemical experiments and began preparing for his electrical researches, he undertook a series of experiments on specific and latent heats, which he recorded in an untitled, indexed packet of 117 numbered octavo sheets. Because the first and earliest date, 5 February 1765, occurs near the end of the record, we assume that the experiments began in 1764.6 Their sequence follows more or less a progression of questions and answers. Cavendish sometimes reordered experiments, but usually he cross-referenced them, and in any case the interruption of chronology is minor and obvious. The bundle of sheets conveys the feel of experimental research leading to important, sometimes unanticipated results. This work was comparable in thoroughness to his experiments on air and on electricity. Because heat enters into the phenomena of most branches of experimental science, we need to know how Cavendish treated it to understand how he approached natural philosophy.
The sheets are not the original slips containing measurements recorded in the laboratory but an intermediate record, from which Cavendish wrote a paper, fifty quarto pages in length, “Experiments on Heat” (not Cavendish’s title). Wilson
When Cavendish came forward as a researcher in the 1760s, the experimental field of heat
Apart from Cavendish’s own work, the important researches on heat were not made in London. He mentioned only one name in his experimental notes, which comes at the very end of the packet, “Martin,”9 clearly a reference to the Scottish physician George Martine
Cullen, the older of the two, was professor of medicine and lecturer in chemistry at the University of Glasgow, in whose laboratory Black worked for a time. When Cullen moved to the University of Edinburgh Black succeeded him in Glasgow, and ten years later Black again succeeded him in Edinburgh as professor of medicine and chemistry, a position he held for over thirty years.12 Prompted by the simple observation by a student that a thermometer cools when it is removed from a solution, and suspecting that evaporation is the cause, Cullen made a series of experiments to find out. He evaporated some thirteen acidic and alkaline liquids, listing them in order of their power to produce cold and obtaining cold of “so great a degree” that he suspected no one had observed it before. He thought that the whole subject should be “further examined by experiment.”13
Stimulated by Cullen’s experiments and by an observation of Daniel Gabriel Fahrenheit’s
In 1760 Black arrived at his second important discovery, specific heats. He was guided to it again by an experiment of Fahrenheit’s reported in Boerhaave’s text on chemistry and also by an experiment in Martine’s essay, both experiments pointing to different heating effects of water and mercury. Black recognized that different kinds of matter communicate heat differently, having different heat “capacities,” another name for which is “specific heats.”16 Specific heat is the heat required to raise the temperature of a given weight of a specific substance one degree; Black used water as the standard substance. Latent and specific heats
Black published nothing of his work on heat, but student notes of his lectures were in circulation by 1767, and an anonymous account of his lectures was published in 1770; in addition his students Adair Crawford
Black’s work can be seen as the beginning of the quantitative study of heat. He agreed with Boerhaave that the thermometer measures heat, but what it measures is the intensity of heat, not the quantity; and he agreed with Boerhaave that heat seeks equilibrium, though in equilibrium the intensity, or temperature, is the same, not the quantity of heat, a confusion Boerhaave made. Black was able to discover specific and latent heats because of his sound method of measuring heat.
If not from the beginning, by the time he wrote up his heat experiments
Cavendish’s experiments on heat were contemporary with Black’s or slightly later. Because Black did not describe his method of measuring specific heats
The paper containing the results, “Experiments on Heat,” is reproduced nearly in entirety in Cavendish’s Scientific Papers, including the first page, which in the manuscript is largely crossed out by Cavendish. On the bottom of that page, separated by a line from the text, perhaps indicating a footnote, is a detail that is not reproduced. The detail, which explains what is otherwise hard to understand by a verbal description, gives the only equation I have found in Cavendish’s scientific papers. It expresses the basic law behind the method of mixtures, as applied to the simplest mixture, hot and cold water:
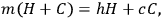
|
15.1 |
where h is the temperature of the hot water, c is the temperture of the cold water, H is the weight of the hot water, C is the weight of the cold water, and m is the temperature of the mixture. He does not work with the equation but by rearranging the terms he writes
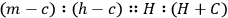 , which is a proportion, the mathematical relation he always works with. Cavendish does not call it a law; instead, he says that “it seems natural to suppose,” crossing that out, “it seems natural to imagine,” and crossing that out, “it seems reasonable to imagine” that the equation correctly describes what happens; the object of his experiments is to find if the proportion “really” is correct. In words, his “experiments were made with an intent to see whether the excess of the heats of the hot water and the mixture above the cold water really bore that proportion [the sum of the weights of the hot and cold water to the weight of the hot water] to each other or not.” (His verbal description is the inverse of the proportion written in symbols above.) He expects the proportion to be confirmed (because it is “reasonable,” elsewhere because it is a “theory”) “if the expansion of the mercury in the therm. is proportional to the increase of heat.”26 It is the instrument that he is investigating here.
, which is a proportion, the mathematical relation he always works with. Cavendish does not call it a law; instead, he says that “it seems natural to suppose,” crossing that out, “it seems natural to imagine,” and crossing that out, “it seems reasonable to imagine” that the equation correctly describes what happens; the object of his experiments is to find if the proportion “really” is correct. In words, his “experiments were made with an intent to see whether the excess of the heats of the hot water and the mixture above the cold water really bore that proportion [the sum of the weights of the hot and cold water to the weight of the hot water] to each other or not.” (His verbal description is the inverse of the proportion written in symbols above.) He expects the proportion to be confirmed (because it is “reasonable,” elsewhere because it is a “theory”) “if the expansion of the mercury in the therm. is proportional to the increase of heat.”26 It is the instrument that he is investigating here.
He next experimented with a mixture of hot mercury and cold water, finding that the heating effect of mercury is equivalent to 31.35 times its weight of water, the standard substance. He then reversed the temperatures, mixing cold mercury with hot water, obtaining a water equivalent for mercury close to the first value. His measured heats of mixtures and the theoretically computed heats agreed to within a half degree, a realistic accuracy for experiments of this kind.27 He continued his experiments with an improved apparatus consisting of a funnel tightly joined to a pan, with stirrers and thermometers inserted in both the funnel and the pan
He carried out experiments on a variety of liquids and solids, taken in part from his shelves of chemical reagents: besides water and mercury, they were spirits of wine, oil of vitriol, solution of pearl ashes, sand, iron filings, shot, pounded glass, marble, charcoal, brimstone, coal, and spermaceti. He also estimated the specific heat of air using a different method, blowing cold air through a worm tube surrounded by hot water.28 His results were contrary to what was expected, as he explained in “Experiments on Heat“: “One would naturally imagine that if cold [mercury] or any other substance is added to hot water the heat of the mixture would be the same as if an equal quantity of water of the same degree of heat had been added; or, in other words, that all bodies heat
He paused at this juncture in the flow of his experiments to carry out an extended investigation of one substance, spermaceti, and with it he changed subjects: “Concerning heat & cold produced by hardening & melting of spermaceti” is the heading of his first experiments on latent heats.32 In the first experiment of this group, he poured melted spermaceti into cold water, hardening it. He calculated that the observed heat communicated to the water would have raised an amount of water equal in weight to the spermaceti by 93.32°. From experiments on the specific heat of spermaceti, he further calculated that if no heat had been generated in hardening, the spermaceti would have communicated 26° of heat to that same quantity of water. The difference of the two numbers gave him the contribution of heat from the change of state
The place that spermaceti had in his researches is evident: it was one of the substances he used to establish a general law or rule of nature. What is unclear is the place it had in his understanding of heat. When he began his experiments, he would have known about the cold produced by evaporation and by melting ice, but we have no way of knowing if he had the idea of a general law of latent heats. It is conceivable that his experiments with spermaceti suggested the idea, in which case there is an element of discovery in his experiments. It is at least equally likely that he already had the idea and that he began with spermaceti for reasons of convenience: it melted at a modest temperature, it had physical qualities he was interested in, and it was a substance at hand. In favor of the second explanation are the substances that he chose to experiment with, which were the same ones that Irvine experimented with: in addition to spermaceti, they were beeswax, another soft substance, and tin and other metals. Against the explanation is Cavendish’s failure to mention any experiments on these substances done by Irvine or anyone else.
Cavendish’s experiments on latent heats established inductively a second law valid for all bodies, which he stated at the beginning of Part 2 of “Experiments on Heat”: “As far as I can perceive it seems a constant rule in nature that all bodies in changing from a solid state to a fluid state or from a non elastic state to the state of an elastic fluid generate cold, & by the contrary change they generate heat.” As in the case of specific heats, Cavendish had an explanation of latent heats: “The reason of this phenomenon seems to be that it requires a greater quantity of heat to make bodies shew the same heat by the thermometer when in a fluid than in a solid state, and when in and elastic state that in a non-elastic state.”34 With his rules of nature and physical explanations, Cavendish had a theory of both specific and latent heats.
Cavendish’s explanation of the change state of a body might be mistaken for Irvine’s
He followed his statement of the law of latent heats with a discussion of experiments that supported it, beginning with experiments on boiling. Cullen had “sufficiently proved” that fluids generate cold when they evaporate at a temperature below the boiling point and are absorbed in the air. Cavendish treated the other “species of evaporation,” boiling, which is independent of the air, finding that 982 degrees of cold are generated in the conversion of water to steam. His discussion of the generation of cold in the change from an inelastic to an elastic state ends with a brief “sketch of the other experiments,” one of which was an attempt to find if cold is generated by dissolving alkaline substances in acids, releasing fixed air. This experiment was original; he gave no details, and his method could not have yielded accurate results, but the principle was sound.37 He next discussed the cold generated in the change from a solid to a liquid state, beginning with the cold generated by melting snow in solutions of sea salt, pearl ashes, spirits of wine, and aqua fortis. He followed this with a discussion of the cold generated by melting spermaceti and beeswax and then by melting “simple metals,” lead, bismuth, and tin, and “mixtures” of these metals. The latter, “alloys,” differed from the simple metals in that they changed state over a range of temperatures rather than at a fixed temperature, analogous to spermaceti and beeswax. He briefly discussed the inverse change of state of these substances, from liquid to solid, generating heat.38 Cavendish’s long series of experiments on specific and latent heats ended here.
Wilson and others have suggested that Cavendish did not publish
Another question is Cavendish’s satisfaction with his experiments and their explanation. Part I of “Experiments on Heat,” which deals with specific heats, is complete and apparently ready to be rewritten in fair copy. The experiments in the incomplete Part II, which deals with latent heats, move beyond heats involved in a change of state of bodies to heats involved in mixing interacting fluids and in chemically releasing fixed air, for which he did not have a “general rule in nature.” The same happened with his experiments on electricity: he completed Part II of his work insofar as it was about experiments explained by the theory of Part I, but he had gone on to make experiments on electrical conduction, which his theory had not addressed. As with his experiments on electricity, he did not bring his experiments on heat to a natural conclusion, but on the contrary, he expanded them.
Cavendish developed a special theory for a specific change of state, evaporation and boiling of water, which he carefully drafted but did not publish.
A preparation for Cavendish’s theory of boiling
Around the time of Cavendish’s theory, Cavallo
Cavendish referred to evaporation and boiling as two “species” of evaporation. Earlier in the century, the first species of evaporation had been explained by a hydrostatic theory, which held that small quantities of water are expanded by heat and rise through the heavier surrounding water. Cavendish accepted the alternative explanation of Charles Le Roy’s
The phenomena of the second species of boiling depend on four “principles,”
To explain the difference between the temperature of boiling and of ebullition, Cavendish introduced a hypothesis
“Theory of Boiling” is a compendium of Cavendish’s scientific practices. It shows him as a natural philosopher
Cold
Extremely cold temperatures
In St. Petersburg in 1759, on a day when the temperature was -34°, a member of the Academy of Sciences J.A. Braun
Cavendish made an extract of a paper with Braun’s repetition of Fahrenheit’s experiments: surprised when the mercury in the thermometer fell hundreds of degrees, and unable to arrive at a consistent freezing point of mercury, Braun said he was confident that it could not be at a “less cold than -346” degrees.56 Braun’s experiments were repeated by Thomas Hutchins
The reason for Hutchins’s findings was evident to two persons in Britain who had clarified to themselves the principles of latent heat, Black and Cavendish. In a letter in 1779 about Braun’s and Hutchins’s experiments, which was forwarded to Hutchins, Black said that frozen mercury
Cavendish drew up a list of experiments to be performed at Hudson’s Bay on the freezing of mercury and on the change of volume of other fluids with temperature.60 In 1781 the Royal Society sent thermometers for use in the experiments, and Cavendish sent an apparatus—a thermometer with the bulb and part of the stem enclosed in a narrow cylindrical cup for holding the mercury to be frozen—for determining the “precise degree of cold at which quicksilver freezes.”61 One day in December 1781, after taking a reading every twenty seconds for about an hour in weather colder than 20° below zero, Hutchins recorded that he “went away to warm myself,” an indication of the rigors of the climate and the limits of endurance of the experimenter.62 In the course of ten experiments on both natural and artificial cold in which he read three instruments—a mercury thermometer, an alcohol thermometer, and the apparatus—Hutchins
Hutchins’s paper appeared in the Philosophical Transactions for 1783, followed by a paper by Cavendish giving his “observations” on Hutchins’s experiments. The experiments confirmed Cavendish’s hypothesis, which was that the great sinking of mercury in thermometers in extreme cold is due to the contraction of mercury. If the earlier reports had been true, the intense cold produced by freezing mixtures would have been “really astonishing,” but they were actually reports of the contraction of mercury. Submerged in freezing mixtures, Hutchins’s thermometer fell to hundreds of degrees below zero, but the cold of the freezing mixture was never less than 46° below zero. The essential point was clearly and simply demonstrated. Because the thermometer in the container of mercury fell to -40°, where it stayed while the surrounding mercury was gradually freezing, the only possible conclusion was that mercury freezes at that temperature. Hutchins came to England and demonstrated his apparatus before Cavendish and Blagden at Cavendish’s house in Hampstead.66 Hutchins returned the thermometers to the Royal Society, where in the best practice of the time, in the presence of witnesses—in addition to Cavendish, they were Hutchins, Banks, Blagden, and Nairne, who made the apparatus—they were examined following the procedure recommended by the boiling point committee of 1777 (Fig. 15.1). Upon making corrections for the fixed point on Hutchins’s thermometers, the adjusted freezing temperature of mercury was declared to be -
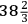 ° or, in round numbers, -39°, in close agreement with the modern value, -38.87°. Hutchins probably did not freeze mercury solid, since the mercury in his thermometer did not fall as far as Braun’s
° or, in round numbers, -39°, in close agreement with the modern value, -38.87°. Hutchins probably did not freeze mercury solid, since the mercury in his thermometer did not fall as far as Braun’s
The new understanding of mercury entered the scientific literature at once. In 1783, the year of Hutchins’s and Cavendish’s publications on mercury, there appeared an English translation of Bergman’s
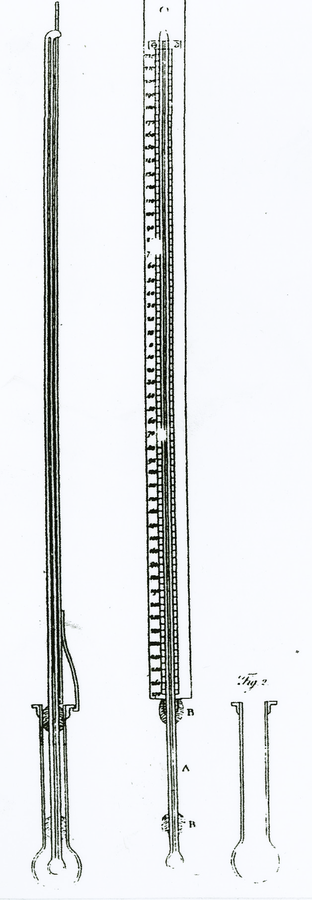
Fig. 15.1: Thermometers for Extreme Cold. The stem and bulb of the middle thermometer extends below the scale. The figure on the left is a side view of the thermometer with the extended stem and bulb inserted into a cylinder holding mercury to be frozen. Thomas Hutchins (1783, *370).
Cavendish made experiments of his own too. Hutchins’s first experiments were read at the Royal Society in the winter of 1775–76, and in January 1776 Cavendish performed experiments on artificial cold
Interested in knowing the greatest cold that could be produced by a freezing mixture of snow and various chemical solutions, and in finding the cause of the cold produced by freezing mixtures, Cavendish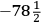 °. Braun claimed that a thermometer filled with spirit of wine (alcohol prepared by distilling wine) sank to -148°, but McNab found that spirit of wine thermometers could not nearly approach that degree of cold. Cavendish published his account of McNab’s experiments in 1786
°. Braun claimed that a thermometer filled with spirit of wine (alcohol prepared by distilling wine) sank to -148°, but McNab found that spirit of wine thermometers could not nearly approach that degree of cold. Cavendish published his account of McNab’s experiments in 1786
We see in Cavendish’s researches on cold qualities of his work we have come to expect. In connection with McNab’s experiments, he published a table of specific gravities of nitric and sulfuric acids corresponding to a range of strengths at a temperature of 60°, which agree with modern theoretical values to the second decimal place. Thorpe considered the table “a striking exemplification of the care, patience and manipulative skill which he spent upon all quantitative determinations.”76
We end this discussion with further conclusions Cavendish drew from McNab’s experiments. The acids could be cooled far below their freezing points without freezing, but once they froze their temperatures rose to the freezing points. In one kind of freezing, nitric and sulfuric acids froze as a whole; in another kind, the watery part of the acids separated out and froze. The acids had complex freezing points, which depended on their strengths. The freezing point of dilute nitric acid was not as low as it was when the acid was made more dilute and also when the acid was not dilute; there was a definite strength of the acid at which it froze with less degree of cold than when the strength was stronger or weaker, which Cavendish called “a point of easiest freezing.” Drawing upon Newton’s method of interpolation, Cavendish determined that the point of easiest freezing was -2.4° Fahrenheit, and that the strength at which nitric acid froze with the least degree of cold was .418 according to his marble scale (he stated the strengths of his acids in terms of the weights of marble dissolved by a unit weight of the acids).77 Sulfuric acid had an even more complicated pattern of freezing. Cavendish found that it had not only a strength of easiest freezing, as James Keir
Cavendish’s first paper on McNab’s experiments cited Lorenz Crell’s
All told, Cavendish published three papers on heat (or cold, which belongs to the same subject), all three presenting experiments done by others, by Hutchins
Heat
The first sentence of Blagden’s contribution to the family obituary of Cavendish reads: Cavendish made himself master of “every part of Sir Isaac Newton’s philosophy.”
The new manuscript was inside a folded sheet labeled in Cavendish’s hand “Heat.” It is a theoretical paper, which he definitely wrote for publication. The first draft he referred to as the “foul copy,” to which he appended a number of pages of additions and alterations, and the revised second draft is a nearly fair copy with some crossings out and certain paragraphs marked for rearrangement for the next writing, which he apparently did not carry out. He referred to the “text,” to which he supplied an apparatus of footnotes, and he called the whole a “paper.” The paper is a mathematical, mechanical theory of heat complete with the principle of conservation of energy and applications to the principal branches of physical science.82
The idea of heat as vibratory motion had received a number of formulations by Cavendish’s time. To the question of what it is that moves, a variety of answers had been proposed: the ordinary particles of bodies, the air and acid sulfur in bodies, the subtle ether, and the fluid of fire. Newton’s authority was invoked in support of more than one of them, but to Cavendish, Newton’s theory meant the vibrations of the ordinary particles of bodies. Many examples of heat in the queries of Newton’s Opticks agree with his answer to the question.83
By the time Cavendish worked out his Newtonian theory of heat, a good many arguments had been marshalled against the view of heat as motion, and we should know what he was up against. One of the arguments was that cold is produced by mixing sal ammoniac and water, whereas in the mixing, particles are set in motion, which should register as heat rather than as cold. A related criticism was the apparent failure of liquids and gases to generate heat upon being agitated.84 The specific heats of bodies were found not to be proportional to their densities, as the motion theory was understood to require. More objections to the motion theory were pointed out by the Jacksonian Professor of Natural Philosophy at Cambridge Isaac Milner
The difficulties of the motion theory could be seen as one general difficulty: new ideas for the theory had not kept pace with the rapid development of the experimental foundation of heat in the late eighteenth century, while the fluid theory of heat had developed together with the experiments.86 Heat was one of a number of hypothetical fluids that had come to characterize British speculative natural philosophy from about the middle of the eighteenth century.87 They were usually taken to be imponderable, indestructible, subtle, and closely associated with fire, and their particles were usually assumed to repel one another and to be attracted to the particles of ordinary substances. The fluid of heat had one quantitative property, the conserved quantity of heat
Black and his followers had the common difficulty of being unable to form an idea of the internal motions of bodies that could account for the phenomena of heat, but Black’s main objection to the motion theory was that none of its supporters had shown how to apply it to the entirety of the phenomena of heat,90 a complaint which could not have been made about the material theory of heat after Cleghorn’s theory
Before proceeding further, we should consider a question readers might have. Because Cavendish successfully developed a theory of electricity based upon a fluid distinct from ordinary matter, it seems that a fluid of heat would have appealed to him as the starting point of a theory of heat. In the case of fluids the analogy
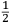 ; in practice vis viva usually appeared with
; in practice vis viva usually appeared with
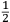 .
.
In Newtonian
Not long before Cavendish entered Cambridge, the Scottish mathematician Colin Maclaurin
Vis viva cannot disappear without giving rise to a comparable effect, an equal quantity of potential motion. This property recommended vis viva for treating a range of mechanical problems, but it encountered difficulties in the case of collisions between bodies. From experience it was known that collisions are never perfectly elastic, implying that vis viva is lost, but it cannot really be lost. The missing vis viva was regarded as continuing on in hidden forms such as the compression of bodies or the motion of parts internal to bodies. Leibniz proposed the latter explanation, but he did not identify the hidden vis viva with heat
In an early unpublished paper, labeled by someone else “Remarks on the Theory of Motion,” Cavendish
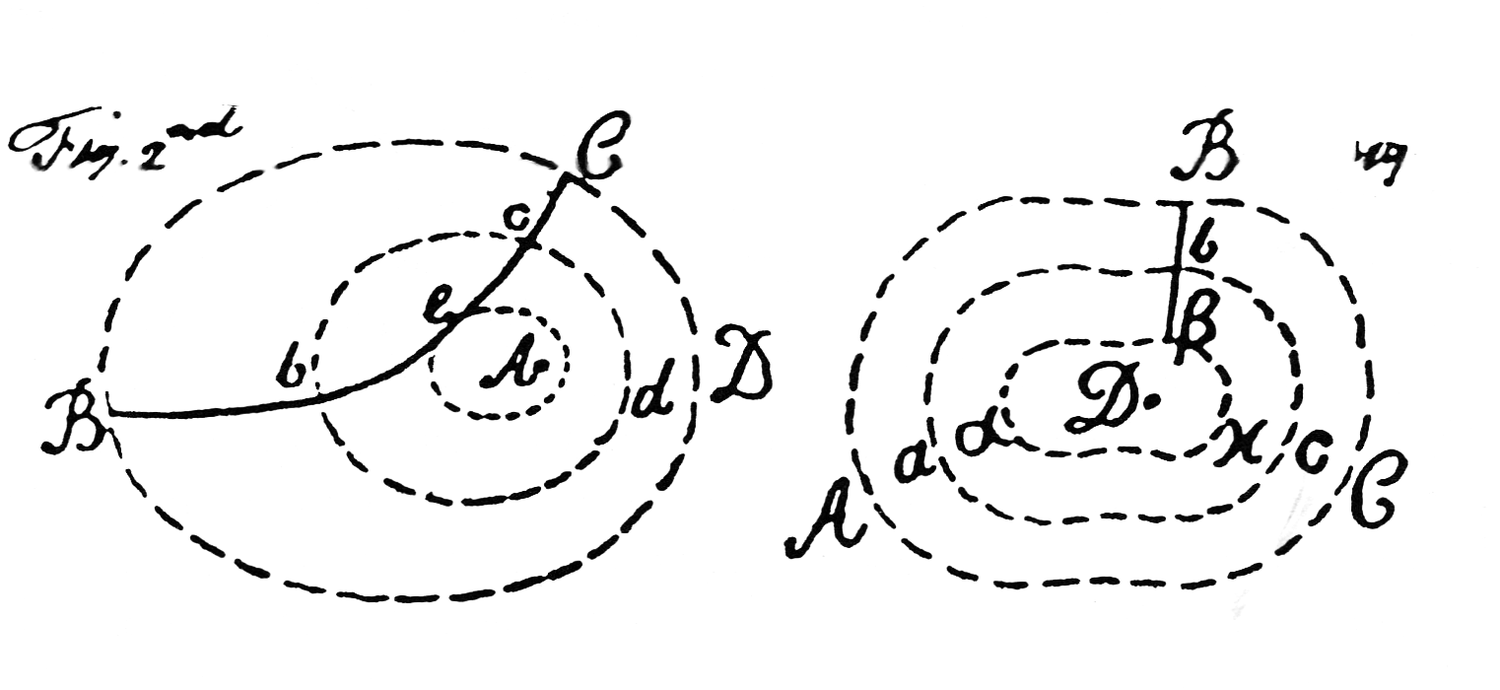
Fig. 15.2: Forces. The dashed lines represent forces of attraction and repulsion of constant intensity centered on bodies or particles of matter, A and D. BC in the figure on the left and Bβ in the figure on the right are paths of a second attracting and repelling body or particle. With the aid of these diagrams and a proposition from Newton’s Principia, Cavendish derived a general law of conservation of the sum of “real” and “additional” “mechanical momenta” (our kinetic and potential energies). It has been pointed out that Cavendish was struggling here with our concept of equipotential curves. “Remarks on the Theory of Motion,” Cavendish Mss VI(b), 7: Plate 3; Sci. Pap. 2:430.
“Heat” carries no date. It was certainly written after 1783, for that year Cavendish rejected Black’s term “latent heat” because it implied the material theory of heat, using instead expressions such as “heat is generated.” In “Heat,” he systematically used “latent heat,” not because his opinion of the fluid theory of heat had changed, but because the expression had become standard, and he was writing to be read. In “Heat,” he used another term he had avoided earlier, “vis viva”
Cavendish begins “Heat” with a purely mechanical investigation, laying out propositions that parallel those in “Remarks,” only developed more systematically and thoroughly. He defines vis viva as the mechanical effect of a body in motion, both “visible” and “invisible.” The visible is the vis viva of the center of mass of a body undergoing progressive motion or of the body undergoing rotation or both; the invisible vis viva is that of the particles of the body moving among themselves; and the total vis viva of the body is the sum of both. He further divides the invisible vis viva into two parts: one is “active,” the other inactive, with the potential for becoming active. His symbol s, standing for the active, is the actual vis viva of all the particles constituting the body; his symbol S stands for one half the sum of the vis viva that each particle would acquire by the attraction or repulsion of every other particle in falling from infinity to its actual position within the body. Upon assuming that the attractions and repulsions between the particles are always the same at the same separations and different at different separations, he derives the law of conservation of vis viva, active and inactive; the quantity s - S cannot change as a result of the motions of the particles among one another. Strictly speaking, the two quantities S and s individually change constantly because of the motion of the particles among one another, but because the number of particles is “inconceivably great” and because any increase in one quantity is matched by a decrease in the other, S and s do not sensibly change, unless there is an external cause.
The first test of Cavendish’s theory is its ability to account for the phenomena of heat itself. When two isolated and unequally heated bodies are brought into contact, one gives up heat
Once he secures the vibrational theory of heat within its own field, heat
A plate of glass is heated more than a plate of polished metal when it is exposed to a fire or the Sun, but since the metal absorbs more light than the glass, according to Cavendish’s theory it ought to be heated more than the glass. To resolve this apparent conflict with the theory, Cavendish refers to recent experiments by Scheele
Heat
Electricity is the field that Cavendish had developed with the greatest thoroughness, and although he had examined the effect of heat
As the final application of his theory, Cavendish discusses the expansion and change of state
Cavendish had a question he could not answer about the change in size of bodies. He said that bodies always expand with heat, but why this is so, and “why the size of the body is never diminished thereby, I do not pretend to explain; but there seems no reason why it may not be so.”107 He seems to have been unaware that below 4°C, water expands with cooling when he wrote this. However, a few years earlier, he was aware of it. In a proposal of experiments on the freezing of mercury for the Royal Society, he wrote: “Water takes up most room when coold almost to freezing than it does at 40° of heat & conseq. a thermometer filled with water stands higher at the former degree of heat then at the latter.” He was concerned that the liquids including mercury used in the thermometers planned for the experiments might behave like water as they approach the degree at which they freeze, which would “make a puzzle in the exper.,” but the remainder of the experiment would show whether or not this is the case.108 Around this time, the singular property of water became well known. In 1797 Count Rumford
The “Conclusion” of “Heat” begins: “It has been shown therefore by as strict reasoning as can be expected in subjects not purely mathematical, that if heat
Cavendish reserves judgment on the opposing theory of heat to the end of the “Conclusion.” Given the evidence for the existence of internal vibrations, he writes, there is no reason to “have recourse to the hypothesis of a fluid
The various hypotheses which have been formed for explaining the phenomena of heat by a fluid seem to show that none of them are very satisfactory; & though it does not seem impossible that a fluid might exist endued with such properties as to produce the effects of heat; yet any hypothesis of such kind must be of that unprecise nature, as not to admit of being reduced to strict reasoning, so as to suffer one to examine whether it will really explain the phenomena or whether it will not rather be attended with numberless inconsistencies & absurdities. So that though it might be natural for philosophers to adopt such an hypothesis when no better offerd itself; yet when a theory has been proposed by Sr I[saac] N[ewton] which, as may be shewn by strict reasoning, must produce effects strongly analogous to those observed to take place, & which seems no ways inconsistent with any, there can no longer be any reason for adhering to the former hypothesis.110
We move on to experiments square feet of surface. He translates this result into its mechanical effect: the rate of vis viva of sunlight falling on that surface exceeds the work done by two horses, that is, it exceeds two horsepower.114 If the same quantity of light were absorbed by a fixed body instead of being reflected, the body would gain an equivalent quantity of heat
square feet of surface. He translates this result into its mechanical effect: the rate of vis viva of sunlight falling on that surface exceeds the work done by two horses, that is, it exceeds two horsepower.114 If the same quantity of light were absorbed by a fixed body instead of being reflected, the body would gain an equivalent quantity of heat
The first experiment is to “expose thermometers
The second experiment is brought up in two places, the first in the preliminary sketch of the paper, where Cavendish speaks of a “calculation”: “Calculation of vis viva of ☉s rays & Do required to commun. given quant. heat.” In the foul copy of the paper, the experiment is described: “Exper“. to determine the vis viva necessary to give a given increase [of] sensible heat to a given body by alternately exposing a thermometer to the ☉ & shading it.”118 The plan of the experiment seems to be this. Cavendish would calculate the vis viva per second of sunlight striking the surface of a blackened thermometer from the measurements in Michell’s
In light of Cavendish’s reputation for anticipating results arrived at only much later by others, we might expect him to have calculated a value for the mechanical equivalent of heat. The value is implicit in his theory, and he apparently had it in mind in the experiment just described. Moreover he had in hand the concepts and units for expressing it: his measure of vis viva is mechanical work, the lifting of weights through a height, our foot-pound, and his measure of the quantity of heat is the same as ours, the heat required to raise the temperature of a unit weight of water 1° by the thermometer, our Brtish thermal unit. A determination of the mechanical equivalent would have made his hypothesis quantitatively complete. A parallel is the hollow-globe experiment, which by establishing the law of electric force made the hypothesis of his electrical theory quantitatively complete. This time Cavendish did not live up to our expectation, and we may ask why.
There is no record that Cavendish performed the experiment with the thermometer. He may have had reservations about Michell’s experiment, which he depended on for calculating the vis viva of sunlight. When Michell performed the experiment, the concentrated rays of the Sun generated a great deal of heat, sufficient to melt the copper vane and disable the apparatus. This may have suggested to Cavendish that the heat of the air on the sunlit side of the vane, not the momentum of light, caused the arm to rotate. In any case that is the explanation of Michell’s experiment, as explained by Abraham Bennett
A value for the mechanical equivalent of heat would have joined a small number of useful physical constants such as the velocity of light and the acceleration of gravity, though as an equivalence it was a different kind of constant. It probably would not have had the importance to Cavendish as it does to us, a possible reason he did not pursue it further. Because he did not express physical relations as equations between terms with physical units, conversion factors and other physical constants did not come up as a matter of course as they do in modern physics; we discuss this point later in connection with the universal gravitational constant G. That he did not place particular importance on the mechanical equivalent of heat in its own right is further suggested by the full description of the experiment: he proposed to determine the vis viva needed to increase the temperature of a body a given amount “& thereby to give a guess at the velocity with which the particles of a body vibrate supposing that the total heat of a body heated to 1000° is double its heat at 0°.”122 From his statement of the problem, we deduce that the average velocity of the particles of the body in meters per second is √4000J, where J is the mechanical equivalent of heat using the Fahrenheit scale for temperature. Inserting today’s value for J, and converting meters to inches, Cavendish’s unit, the average velocity of the particles of the body at 1000° is about 6800 inches per second. Cavendish would have found J from Michell’s experiment and his own experiment exposing a blackened thermometer to the Sun, discussed above. Cavendish’s estimate of the velocity of particles points to his interest in the physical reality described by Newton’s theory of heat.
As to the immediate stimulus for writing the paper, Cavendish said nothing
In 1785 Fordyce published an experimental paper in the Philosophical Transactions demonstrating a loss of weight by ice upon melting
There are, however, several circumstances that may have affected his decision. The first is a widening interest in heat
The fifth circumstance is the state of natural philosophy
The final circumstance is the abundant practical applications
If Cavendish had carried out his original intention, he would have submitted his paper
That question is asked about Cavendish’s other work too, but in the case of “Heat,” the question is unavoidable, for unlike many of his researches, he intended this one for publication from the start. Perhaps Cavendish did not want to enter into rivalry, usually the first guess. This can be ruled out, since in his lifetime no similar work was published. Experiments on the mechanical equivalent of heat began to appear only in the 1840s, and publications on the mechanical theory of heat only in the 1850s. After a brief discussion by Daniel Bernoulli in the early eighteenth century, the next publication on the kinetic theory of gases came out after Cavendish had been dead for six years, and it did not identify heat with vis viva but with momentum. Because Newton’s theory of heat was out of favor, Cavendish might have wanted to avoid the criticism that was certain to follow. However, he had allies. His colleague Thomas Young said in 1807 that the “most sober reasoners of the present” subscribe to the vibration theory of heat.136 Perhaps Cavendish had unanswered questions. Where he discussed the heat of electrical discharge and the latent heat of the wire, he noted, “This must be examined.”137 But he had questions of the same sort when he began, as we know from preliminary notes he made for his paper. Nothing suggests that he found any disagreement with experiment. The mathematical development of his theory of heat fell short of that of his electrical theory, and explanations of phenomena were largely qualitative, but he knew that at the beginning too, and in his published paper on electricity he applied his theory to phenomena only qualitatively. The theory of heat did not obviously point to a new class of phenomena in the way the theory of electricity did, but it laid the foundation for the next stage of the science of heat. With reference to Cavendish’s unpublished papers, Blagden said that “it is to be supposed that he afterwards discovered some weakness or imperfection in them.”138 General as it is, it is the best explanation we are likely to get
The Natural Philosopher
Cavendish had mastered Newton’s science, but he needed more than Newton gave him to make “Newton’s theory of heat,” and important as Leibniz’s vis viva was, that did not give it to him either. Rather Cavendish drew on these sources and on his and others’ experiments on heat, and by strict reasoning he brought them together to make the theory he presented in “Heat.”
There are various ways of showing why Cavendish is seen as a natural philosopher, and “Heat” is one of them. “Philosophy,” the natural philosopher and geologist James Hutton
In “Heat” Cavendish tells how he thinks the physical universe is constituted. The totality of the material world and its activity arise from attractive and repulsive forces
According to father Boscovich & Mr Michell matter does not consist of solid impenetrable particles as commonly supposed, but only of certain degrees of attraction & repulsion directed toward central points. They also suppose that the action of 2 of the central points on each other alternately varies from repulsion to attraction numberless times as the distance increases. There is the utmost reason to think that both of these suppositions are true; & they serve to account for many phenomena of nature which would otherwise be inexplicable. But even if it is otherwise, & if it must be admitted that there are solid impenetrable particles, still there seems sufficient reason to think that those particles do not touch each other, but are kept from ever coming in contact by their repulsive force.141
Matter likely is nothing other than centers of force. Cavendish thinks that Boscovich
Boscovich published his idea of forces in his Theoria philosophiae naturalis in 1758.143 Michell arrived independently at a similar idea, which his friend Priestley published in his history of optics in 1772.144 There was a British tradition paralleling Boscovich’s idea,145 which may have been more important, though Boscovich developed the concept of central points interacting through central forces in greatest detail. In Boscovich’s theory of natural philosophy, at close separations central points experience infinite repulsion; at large separations they experience gravitational attraction; and in between they experience attractions and repulsions responsible for cohesion, vaporization, and a variety of other chemical and physical phenomena. He represents his universal “law of forces” by a continuous curve: above the axis the force is repulsive, below the axis it is attractive, and places where it passes between repulsion and attraction mark the limits of cohesion. When disturbed, central points vibrate around these places, and the vibrations continue indefinitely until the central points are again disturbed. The area between the curve and the axis is proportional to vis viva, the measure of the action of the force across a distance. In a general way, Boscovich’s
Bodies act on bodies across a distance. Blagden recorded in his diary that Cavendish
Another aspect of Cavendish’s Newtonianism placed him not in the vanguard of but in opposition to the next development in science. In America, Francis Hopkinson
As Young understood him, it was “Newton’s opinion, that heat consists in a minute vibratory motion of the particles of bodies, and that this motion is communicated through an apparent vacuum by the undulations of an elastic medium, which is also concerned in the phenomena of light.”153 Young’s understanding pointed to the physics of the ether, the origin of unified views of nature in the nineteenth century. Cavendish’s understanding of Newton’s opinion did not include an ether, or if it did he never mentioned it. So far as we know, he held to the view that the phenomena of nature have a uniform cause in attractive and repulsive, centrally acting forces. This view, together with mechanical theorems about the measure of the force of moving bodies, vis viva, permitted him to display a connectedness between the several major domains of phenomena constituting the broad field of natural philosophy
Workplace
Cavendish was able to develop a comprehensive theory of heat because of his exhaustive experimental study of heat, as described earlier in this chapter. To judge from the laboratory record of his experiments on heat, and that of his experiments in other fields, he spent as much time in the laboratory as he did in his study. For a few laboratories of the time, there exist drawings. We do not have one of Cavendish’s, but we have the next best, sketches he made of various apparatus, which give the reader an idea of what he would have seen if he had entered his workplace. Or what would have greeted her: John Davy
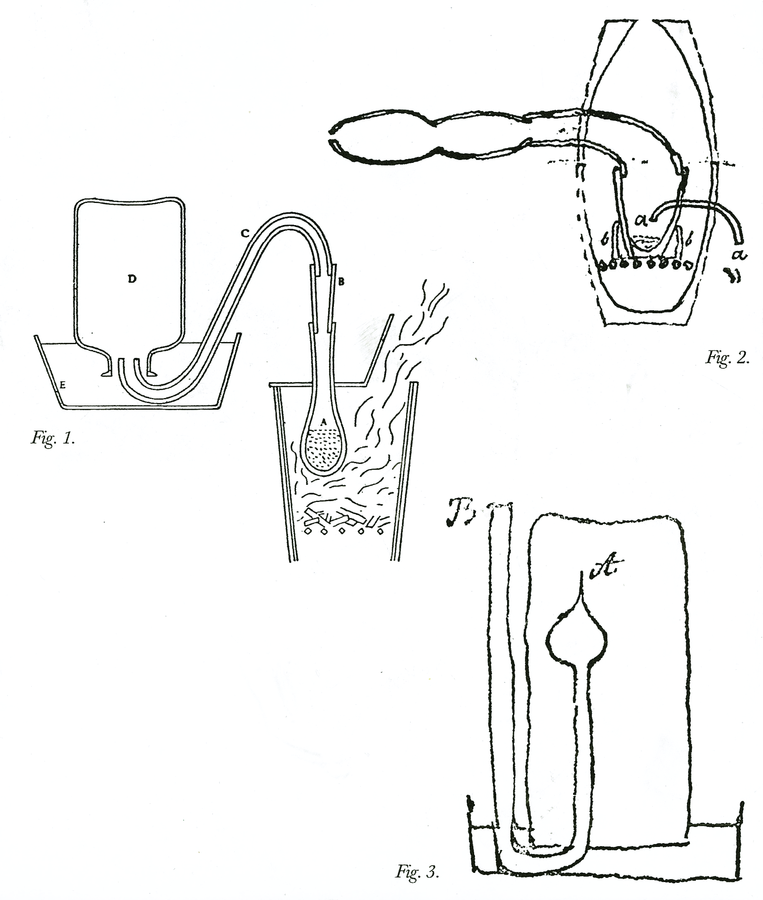
Fig. 15.3: Laboratory Apparatus. Figure 1. Apparatus for distilling vegetable and animal substances. A bottle for collecting air D is filled with water and then is inverted into vessel E filled with water. The Scientific Papers of the Honourable Henry Cavendish, ed. E. Thorpe, 2 vols. (Cambridge: Cambridge University Press, 1921) 2:308; hereafter in the captions Sci. Pap. Figure 2. Apparatus for subliming arsenic in a crucible, with a set of aludels attached, placed within a reverberatory furnace. Cavendish Mss II, 1(b): 21. Figure 3. Apparatus for measuring the expansion of air with heat; the bent tube contains mercury and air. Cavendish, Sci. Pap. 2:374. Reproductions by permission of the Chatsworth Settlement Trustees.
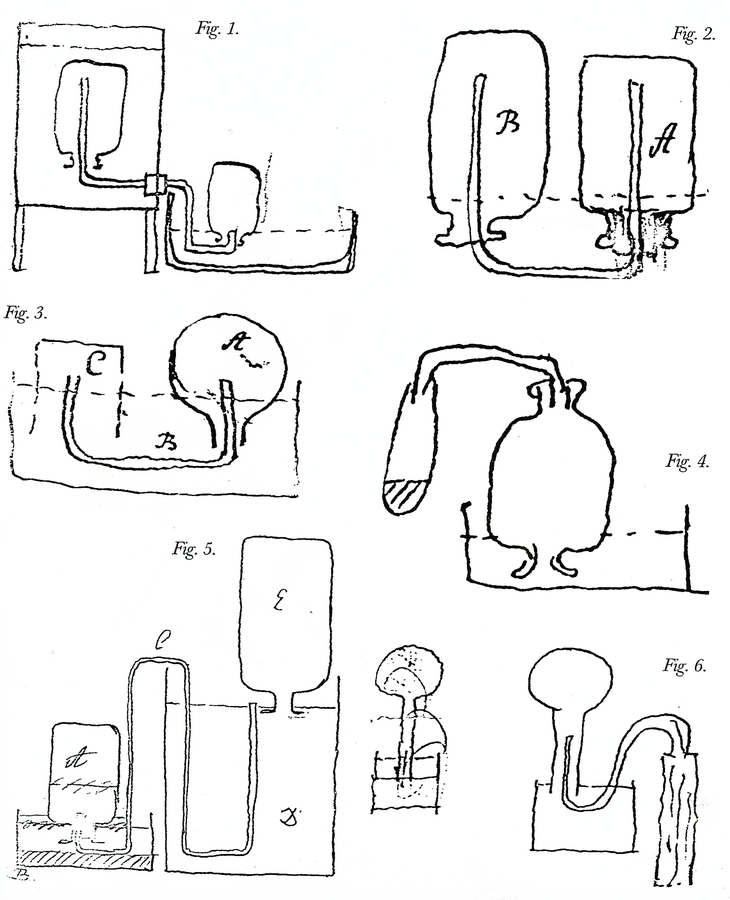
Fig. 15.4: Laboratory Apparatus. Figure 1. Apparatus for an experiment to decide if heavier airs in a mixture of airs settle to the bottom. The mixture is contained in the bottle on the left, and as water is gradually let into it, different samples are caught in bottles on the right. Cavendish Mss II, 5:102. Figure 2. Apparatus for eudiometer experiments. Bottle B is filled with nitrous air, bottle with common air. Ibid. 5:42. Figure 3. Sulfur is burned in the glass globe A, and the air that is forced out by the heat is caught in jar C and examined, as part of Cavendish’s eudiometer tests. Ibid. 5:61. Figure 4. Apparatus for capturing air upon boiling burnt charcoal with spirit of niter. Ibid. 5:345. Figure 5. Apparatus to determine if fixed air is produced by mixing common or dephlogisticated air in bottle A with nitrous air in bottle E. Ibid. 5:5. Figure 6. Apparatus to determine the effect on the volume of dry air by saturating it with moisture. Cavendish Mss Misc. Reproductions by permission of the Chatsworth Settlement Trustees.
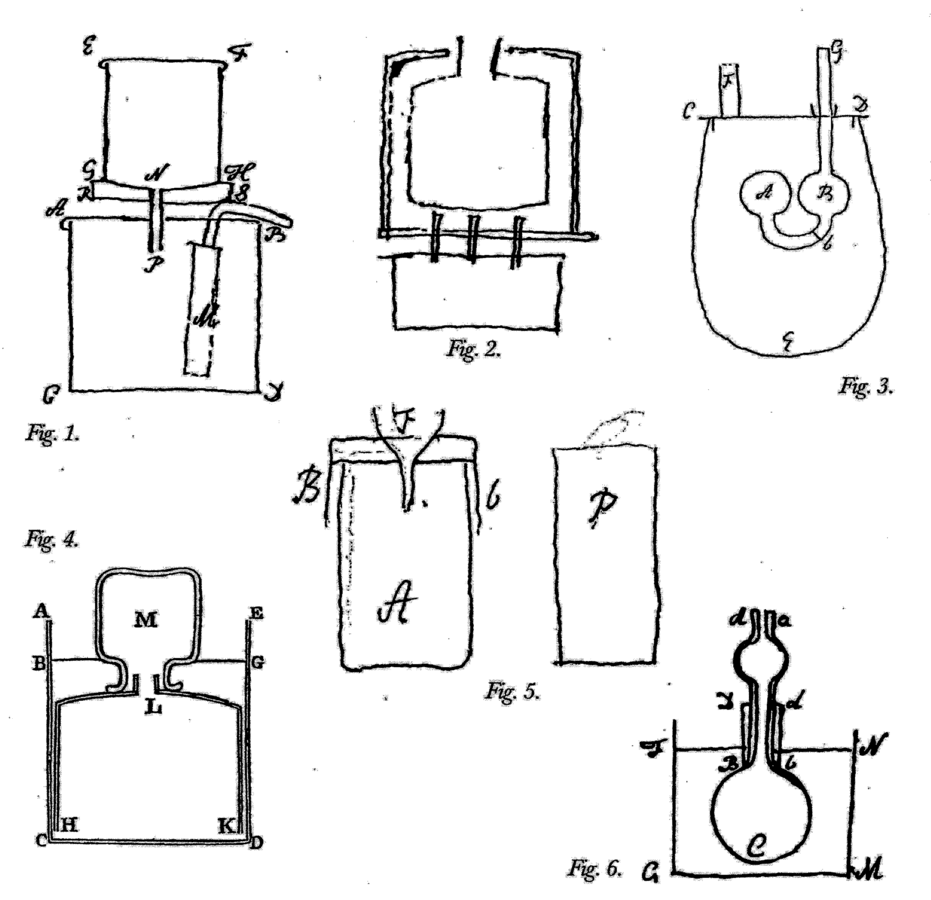
Fig. 15.5: Laboratory Apparatus. Figure 1. Apparatus for experiments on the heats of mixtures. Through the cylindrical funnel on top, hot water is added to cold water in the pan below; M is a stirrer. Untitled paper on experiments on specific and latent heats, Cavendish Mss. Figure 2. Apparatus for determining the time of evaporation of boiling water. The water is contained in a tin bottle surrounded by an insulated tin frame and placed over a spirit lamp. Cavendish Mss III(a), 9:42. Figure 3. Apparatus to decide if the heat at which water becomes steam is the same as the heat of the steam. The ball A, which contains a little water and otherwise is filled with mercury to b, is exposed to steam and to the boiling water. Ibid. 1:1. Figure 4. Apparatus for collecting air discharged from pump water when it is boiled; the water is in ACDE, the air in M. Cavendish, Sci. Pap. 2:105. Figure 5. Apparatus to find the weight of fixed air in calcareous earth. Acid is poured through the funnel onto a sample of the earth contained in cylindrical glass A; after effervescence, the plug P is drawn in and out of the empty part of A to drive out any residual fixed air. Cavendish Mss II, 5:379. Figure 6. Apparatus to determine if the electrical charge of coated glass is the same whether hot or cold. The glass bowl C is filled with mercury as is the surrounding vessel, making it a Leiden jar, the charge of which is tested while a thermometer is dipped into the mercury at different heats. Cavendish, Electrical Researches, opposite p. 180. Reproductions by permission of the Chatsworth Settlement Trustees.
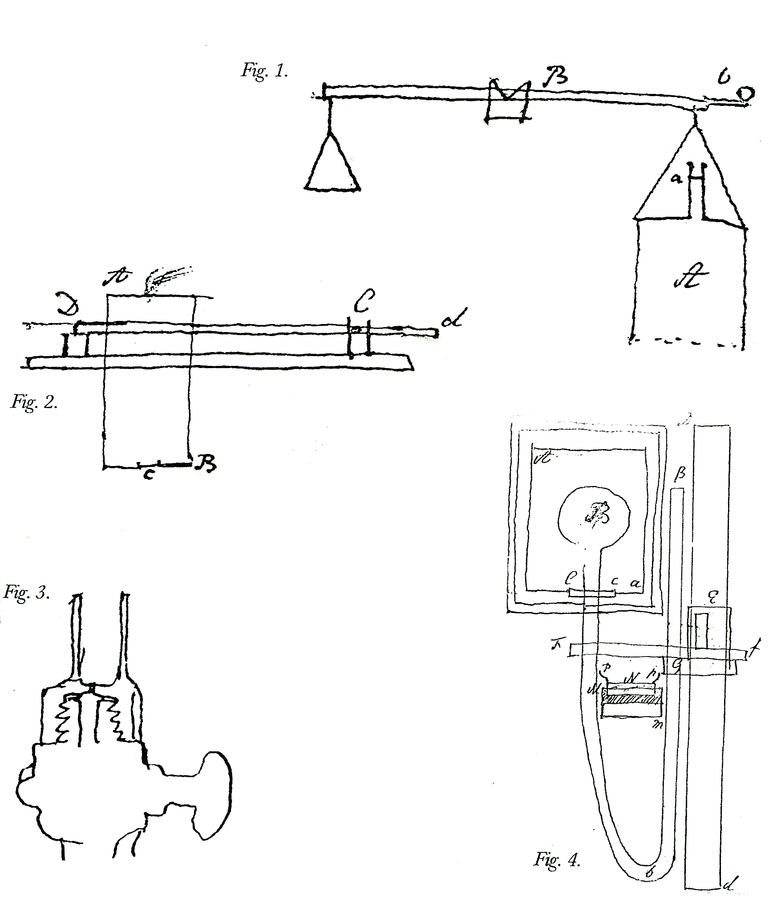
Fig. 15.6: Laboratory Apparatus. Figure 1. Apparatus to test if the vis inertiae of phlogisticated air is the same in proportion to its weight as that of common air. The method requires finding the time in which a given quantity of air contained in A passes through a small hole at the top under a given pressure. Cavendish, Sci. Pap. 2:321. Figure 2. Apparatus for measuring the strength of the detonation of inflammable air with other airs. Air is admitted into the brass cylinder AB and electrically fired, lifting the pivoted board Dd to which it is fixed. Cavendish Mss II, 5:130. Figure 3. Apparatus for measuring the cold produced by the rarefaction of air. The brass cock is screwed over the cock of the condensing glass of an air pump. The ball of a thermometer is fitted into the cylinder of the cap, a small hole at the bottom of which allows the escaping condensed air to blow on the ball. Cavendish Mss III(a), 8:11. Figure 4. Apparatus for finding the “force of steam,” or tension of aqueous vapor, at heats below 212°. A small amount of water stands above the mercury in Bb. The tin pot Aa contains heated water. Cavendish, Mss III(a), 1:40. Reproductions by permission of the Chatsworth Settlement.
Footnotes
Benjamin Thompson (1798); in (1870–1875, 1:491).
Joseph Black (1803, 1:11–12).
Douglas McKie and Niels H. de V. Heathcote (1958, 13–15).
Cavendish Mss III(a), 9:89. On pp. 92 and 94, there are two more dates, both in 1776; the experiments involve freezing mixtures.
This paper is published: Henry Cavendish (1921c). The manuscript of the paper consists of 41 numbered pages followed by 9 unnumbered pages. The numbered pages are complete, but the remaining ones are sketchy.
Cavendish Mss III(a), 9:114.
In Glasgow Black was professor of anatomy but soon exchanged duties with the professor of medicine. In Edinburgh Cullen took over the chemistry chair in 1766, freeing the chair of medicine and chemistry, which Black took over. In Scottish universities, there was a good deal of shuffling of chairs. Ramsay (1918, 31, 47).
Cullen’s paper was first published in 1755 in Edinburgh Philosophical and Literary Essays and was republished together with Black’s essay: Experiments upon Magnesia Alba, Quick-lime, and Other Alkaline Substances; by Joseph Black. To Which Is Annexed, An Essay on the Cold Produced by Evaporating Fluids, and of Other Means of Producing Cold; by William Cullen (1898, 132).
McKie and Heathcote (1935, 16, 35). Henry Guerlac (1970, 177). A.L. Donovan (1975, 238–240).
Donovan (1975, 240–246).
Guerlac (1970, 178–179).
The Swedish physicist Johan Carl Wilcke discovered latent heat independently of Black and later, in 1772. Unlike Black he published his work on latent and specific heat, discussed in McKie and Heathcote (1935, 54–121).
Schofield (1970, 188–189). By his method, Black measured “heat exchanges in terms of a temperature change of so many ‘degrees of heat on Fahrenheit’s scale’ for an equal mass of water.” McKie and Heathcote (1935, 122).
Cavendish wrote: “Dr Cullen has sufficiently proved that most if not all fluids generate cold by the first species of evaporation.” By “first species,” Cavendish meant evaporation produced by heating a liquid without boiling it, which he attributed to absorption by the air. Cavendish (1921c, 344).
Guerlac (1970, 177–178). Fahrenheit was an instrument maker, a friend of Boerhaave’s, and a fellow of the Royal Society, who published papers on meteorological instruments in the Philosophical Transactions.
Brook Taylor was a mathematician and fellow of the Royal Society, whose experiments were reported in the Philosophical Transactions for 1721; they are described in A. Wolf (1961, 1:189–190). Wilson (1851, 447).
Cavendish (1921c, 327). Wilson (1851, 447). Black began his experiments the same way, by examining the thermometer. Guerlac (1970, 177–178).
Cavendish, “Experiments on Heat,” Mss III(a). On p. 1 in the manuscript. In the equation and proportion, the parentheses are added.
Cavendish Mss III(a), 9:48–56.
Cavendish (1921c, 341–343). He used a worm tube again in his experiments on latent heat, finding the heat generated by condensing water vapor, and mentioning Black. Ibid., 346–347.
Ibid., 332.
Cavendish (1921c, 340).
Cavendish Mss III(a), 9:22, 27.
Ibid., 32.
Cavendish (1921c, 343).
Nowhere does Cavendish mention Irvine by name, but his manuscripts contain two short memoranda directed to principal points of Irvine’s theory. One states a proposition that any heat that appears in bodies depends entirely on their heat capacities and changes in them. The proposition is expressed in the language of the material theory of heat, its only appearance in any of Cavendish’s papers: heat is said to be “absorbed” by bodies and “united” to them. The second memorandum is an experimental “compleate proof” that the absolute heat in bodies is not proportional to their specific heat, as Irvine’s theory requires. There is a second copy in Cavendish’s hand of the second memorandum in Blagden’s papers, suggesting Blagden as a possible reason he wrote out the proof. Henry Cavendish, “That All the Heat Which Appears in Bodies …”; “A Complete Proof that the Quantity of Heat …” Cavendish Mss Misc. Blagden Collection, Misc. Notes, Royal Society, 93.
Cavendish (1921c, 351). “Thoughts” is an unnumbered page in the manuscript.
Cavendish Mss III(a), 9:39–40.
Jean André Deluc to Henry Cavendish, 19 Feb. 1777; in Jungnickel and McCormmach (1999, 546, 549).
Cavallo (1781, 505–507).
Cavendish, “Theory of Boiling,” 354–356.
Ibid., 358–360.
Ibid., 361–362.
John Fothergill (1748, 258–260). William Watson (1753a, 108–109).
“Account of Freezing of ☿ from Pallas Journey into Siberia,” extract in Cavendish’s hand, Cavendish Mss III(a), 15. Pyotr Simon Pallas (1771–1776).
This extract in Cavendish’s hand is an account of experiments by several Petersburg academicians following Braun’s discovery; in English translation from the French by James Parsons (1760).
Joseph Black to Andrew Graham, 5 Oct. 1779, published by Thomas Hutchins, in “Experiments for Ascertaining the Point of Mercurial Congelation” (1783, 305–306). Black did not know that Cavendish had recommended a similar apparatus to Banks. Henry Cavendish (1783b).
Cavendish (1783b, 146).
There are several drafts of instructions in Cavendish’s papers, most of them in Cavendish Mss III(a), 4 and 14. The first group is mainly concerned with Hutchins’s experiments published in 1783, though it contains some subsequent instructions sent in 1784. The second group is concerned with the next series of experiments at Hudson’s Bay Company, conducted by John McNabb, published in 1786 and 1788. In addition, there are unclassified papers on the Hudson’s Bay experiments in the miscellany of Cavendish’s manuscripts.
Cavendish (1783b, 145, 148–149).
Thomas Hutchins to Charles Blagden, n.d., “Monday Morning,” Blagden Letters, Royal Society, H.59.
Cavendish (1783b, 157).
The disparity between the two numbers for the low reading, -654 and -634, is in the text. Torbern Bergman, Outlines of Mineralogy, trans. W. Withering (Birmingham, 1783), 71, 83.
Entry for 22 Jan. 1776, Cavendish Mss III(a), 9:94–96.
Blagden was with Cavendish. The following day he recorded in his diary that Cavendish had frozen mercury, and he mentioned it in his history of the freezing of mercury. 27 Feb. 1783, Charles Blagden Diary, Royal Society, 1. Blagden (1783, 359–360).
Charles Blagden to Erasmus Darwin, 14 Sep. 1786, draft, Blagden Letters, Royal Society 7:34. Charles Blagden to Mrs. Grey, 30 Jan. 1788, ibid. 7:111.
Henry Cavendish (1786, 195, 197–198, 210).
Thorpe (1921, 59–60).
Cavendish (1788a, 218).
Wilson (1851, 461–465). Berry (1960, 150–154, quote on 154). Cavendish (1788a, 223).
Cavendish (1783b, 150–151). The discussion of heat in this section draws on Russell McCormmach (1988). We acknowledge permission to use the material: University of Chicago Press, copyright 1988 by the History of Science Society, Inc., all rights reserved.
Cavendish (1784b, 173–174).
The revised draft of “Heat” consists of forty-three pages of text and notes, one page of diagrams with an accompanying page of explanation, and one page of additions and alterations. The original manuscript of both drafts of “Heat” is located in the Public Archives of Canada in Ottawa. The manuscript is published in Russell McCormmach (2004, 153–193). The page numbers of “Heat” in the following footnotes refer to the manuscript unless otherwise specified.
Robert E. Schofield (1970, 13, 37, 48, 77–78, 84–85, 139, 160, 179, 183). Isaac Newton (1952, 348–349, 375–406).
William Irvine (1805, 21–23).
L.J.M. Coleby (1954, 242–252).
Robert Fox (1971, 19, 22–23).
J.L. Heilbron (1993a, 5–33. Schofield (1970, 157–190); P.M. Heimann (1981, 67–73). Arthur Quinn (1982, 127); McKie and Heathcote (1958). Fox (1971, 19–20, 22, 25).
Schofield (1970, 186–187). Irvine (1805, 22)
P.M. Heimann and J.E. McGuire (1970, 225–227).
Colin Maclaurin (1742, 2:427, 433–434).
Erwin N. Hiebert (1962, 80–93). P.M. Heimann (1977).
The paper Smeaton gave Cavendish to comment on was probably “New Fundamental Experiments upon the Collision of Bodies” (1782). J.G. Playfair (1822, 1:lxxxiii).
Bernoulli first and then Smeaton called it “mechanic force.” Newton treated the square of the velocity in the Principia, but he did not name it. W.H. Wollaston (1806, 16).
Cavendish, “Heat,” 23. Experiments on “heat rays” and light using polished metal and glass, discussed in Carl Wilhelm Scheele (1780, 72–74, 92–98). Saussure’s account of experiments that he and M.A. Pictet carried out on the reflection of “obscure heat” emitted by hot, but not red hot, bodies, discussed in Saussure (1786, 354–355).
For example, Pierre Prevost’s experiments on heat rays and Benjamin Thompson’s on the mechanical production of heat in the 1790s would have been relevant to Cavendish’s argument, as perhaps would Herschel’s experiments on radiant heat from 1800.
Cavendish did not formally introduce a term for “specific heat”; he spoke of the “capacities for heat” of bodies. “Specific heat” first appeared in print in a publication by J.H. Magellan in 1780. Both terms are still used. Cavendish, “Heat”, 11–12, 24, 41.
Ibid., 14–16.
Ibid., 18–20, 25–26.
Ibid., 23–24.
Ibid., 26–31, on 31.
Cavendish, “Heat,” 41.
Ibid., 38–39.
Cavendish, “Heat,” in McCormmach (2004, 101, 231).
Henry Cavendish, “List of some Exper. …,” Cavendish Mss III(a), 4(a).
Benjamin Thompson, Count Rumford, “On the Propagation of Heat in Fluids” (1870–1875, 1:239–400, on 308–33). Tiberius Cavallo referred his readers to Rumford’s discussion of this exceptional property of water (1803, 3:35–37).
Cavendish, “Heat,” 42.
Joseph Priestley (1767, 1:387–389). Cantor (1983, 57). S.G. Brush and C.W.F. Everett (1969).
Cavendish, “Heat,” 22.
Tiberius Cavallo (1780, 591–594).
Cavendish, preliminary sketch and foul copy, “Heat,” in McCormmach (2004, 153, 162).
Abraham Bennett (1792, 87–88).
Heintz Otto Sibum (1995, 73–74, 104–105).
Young (1807, 1:655).
Antoine Laurent Lavoisier and Pierre Simon Laplace (1982, 4–6). Henry Guerlac (1976, 244–248). Charles Blagden to A.L. Lavoisier, draft, 15 Sep. 1783, Blagden Letterbook, Yale.
Charles Blagden to Pierre Simon Laplace, 5 Apr. 1785, draft, Blagden Letterbook, Yale; Charles Blagden to Lorenz Crell, 28 Apr. 1785, draft, ibid.
Sanborn C. Brown (1979, 219–220).
John Roebuck (1776). These experiments, witnessed by Cavendish among others, showed an increase of weight in iron and silver upon cooling, a result in agreement with Fordyce’s later experiment. Charles Blagden to Henry Cavendish, n.d., [1785]; in Jungnickel and McCormmach (1999, 608–609).
27 Feb. 1783, Charles Blagden Diary, Royal Society. Charles Blagden to Erasmus Darwin , 14 Sept. 1786, draft, Blagden Letters, Royal Society 7:34. Henry Cavendish (1921b).
Bryan Higgins (1786, 301–302).
Fox (1971, 23, 28).
William Nicholson (1781, 1:134; 1790, 6).
Fox (1971, 19–20, 23, 104–105).
John Leslie (1804, 140–141).
Blagden, upon delivering to Cavendish a gift of René-Just Haűy’s new treatise on electricity and magnetism, which contained an electrical hypothesis similar to Cavendish’s, observed that the author seemed unaware of Cavendish’s paper of 1771: Charles Blagden to Claude Louis Berthollet, 11 Sep. 1787, draft, Blagden Letters, Royal Society 7:69.
Young (1807, 1:656). In addition to Young, they included Humphry Davy, Benjamin Thompson, and Cavendish. Schofield (1970, 290–295).
Blagden, in the family obituary of Henry Cavendish.
“Heat” disproves Yukitoshi Matsuo’s assertion of Cavendish’s “failure to unify a variety of heat phenomena in terms of dynamics and his subsequent abandonment of a systematic consideration of them” (1975, 93–94).
Cavendish, “Heat,” in McCormmach (2004, 187–188).
He introduced it in his theory of boiling. Cavendish, “Theory of Boiling,” 361. He used it to reconcile his theory of electricity with experiments. Maxwell in Cavendish (1879, 174–175). He analyzed the error of a magnetic dipping needle by assuming that the axis of the needle and the plane on which it rolls are prevented from actually touching by a repulsive force. Henry Cavendish, “On the Different Construction of Dipping Needles,” Cavendish Mss IX, 40:12–14. In “Heat,” he used the idea to resolve difficulties with the heat of friction in his theory of heat, and he used it to derive the general law of conservation of energy, which applies to forces and heat wherever they appear in natural philosophy.
Cavendish would have read about Boscovich’s force in his Theoria. Cavendish and Michell met Boscovich on his tour of England, both dining with him at the Royal Society Club on 5 June 1760, and Cavendish with him again on 26 June 1760: Minute Book of the Royal Society Club, Royal Society, 4.
Priestley (1772c, 1:309–311, 392–393, 786–791).
Cantor (1983, 71–72); Schofield (1970, 237–238); P.M. Heimann and J.E. McGuire (1971, 233–306).
It makes no difference here that Boscovich believed in the matter of fire; Roger Joseph Boscovich (1966, 22–23, 43, 73, 76–96). Boscovich did not have a conservation law and he generally regarded vis viva as having little significance. Thomas L. Hankins (1965, 294), and on Boscovich, 291–297; on Michell and Boscovich, Schofield (1970, 36–49).
22 Nov. 1804, Charles Blagden Diary, Royal Society 4:284.
Francis Hopkinson to Thomas Jefferson, 14 Apr. 1787; in Boyd (1955, 288–290). Brooke Hindle (1964, 276–277). John C. Greene (1984, 158–160). 6 Nov. 1794, Certificates, Royal Society 5.
Sci. Pap. 2:437. The calculation is undated, but an inspection of the watermark on the paper shows that it could not have been earlier than 1804.
Wilson (1851, 178–179).
