The NETZSCH software suite intended for use in kinetic calculations from thermoanalytical data is based on the above principles. It naturally has specific features and computational procedure. Let us consider the software design philosophy and operational principles. In this workbook, Netzsch Proteus® 4.8.3 and Netzsch Thermokinetics® 3.0 versions are used to demonstrate main operating procedures. As Netzsch continuously improve software, we strongly recommend using actual versions of Proteus® and Thermokinetics®. New versions of software always include basic procedures presented in this workbook, as well as new useful functions.
3.1 Inverse Kinetic Problem
The inverse kinetic problem is solved with the use of model-free Friedman [6] methods and Ozawa–Flynn–Wall [7,8] methods. The model-free methods (Friedman analysis, Ozawa–Flynn–Wall analysis, evaluation according to ASTM E698) are applied to non-isothermal kinetic analysis when experimental data is represented as the set of measurements at different heating rates. The model-free methods provide information on kinetic parameters, such as the activation energy and preexponential factor, without determining a concrete kinetic model. The Arrhenius parameters obtained by these methods are used as starting approximations in solving the direct kinetic problem. This solution makes it possible to find the type of function approximating the experimental data and to refine the Arrhenius parameters.
In thermal analysis, the concept of conversion is used. NETZSCH ThermoKinetics software operates with partial mass loss (for thermogravimetry), and partial area (for DSC, DTA and mass spectrometry) rather than with the common term conversion degree.
For integral measurements (thermogravimetry, dilatometry), the measured curve is converted to the plot of conversion αi versus time ti by Equation 3.1:
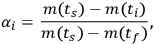
|
3.1 |
where (ts) is the signal at the starting moment of time ts, m(ti) is the signal at the ith moment of time ti, and m(tf) is the signal at the final moment of time tf.
For differential measurements (DSC, DTA, mass spectrometry), the conversion is calculated by Equation 3.2:
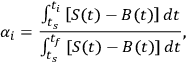
|
3.2 |
where S(t) is the signal at the moment of time t and B(t) is the baseline at the moment of time t.
3.1.1 Friedman Method
The Friedman method is a differential one, where the initial experimental parameter is the instantaneous rate dαi/dti.
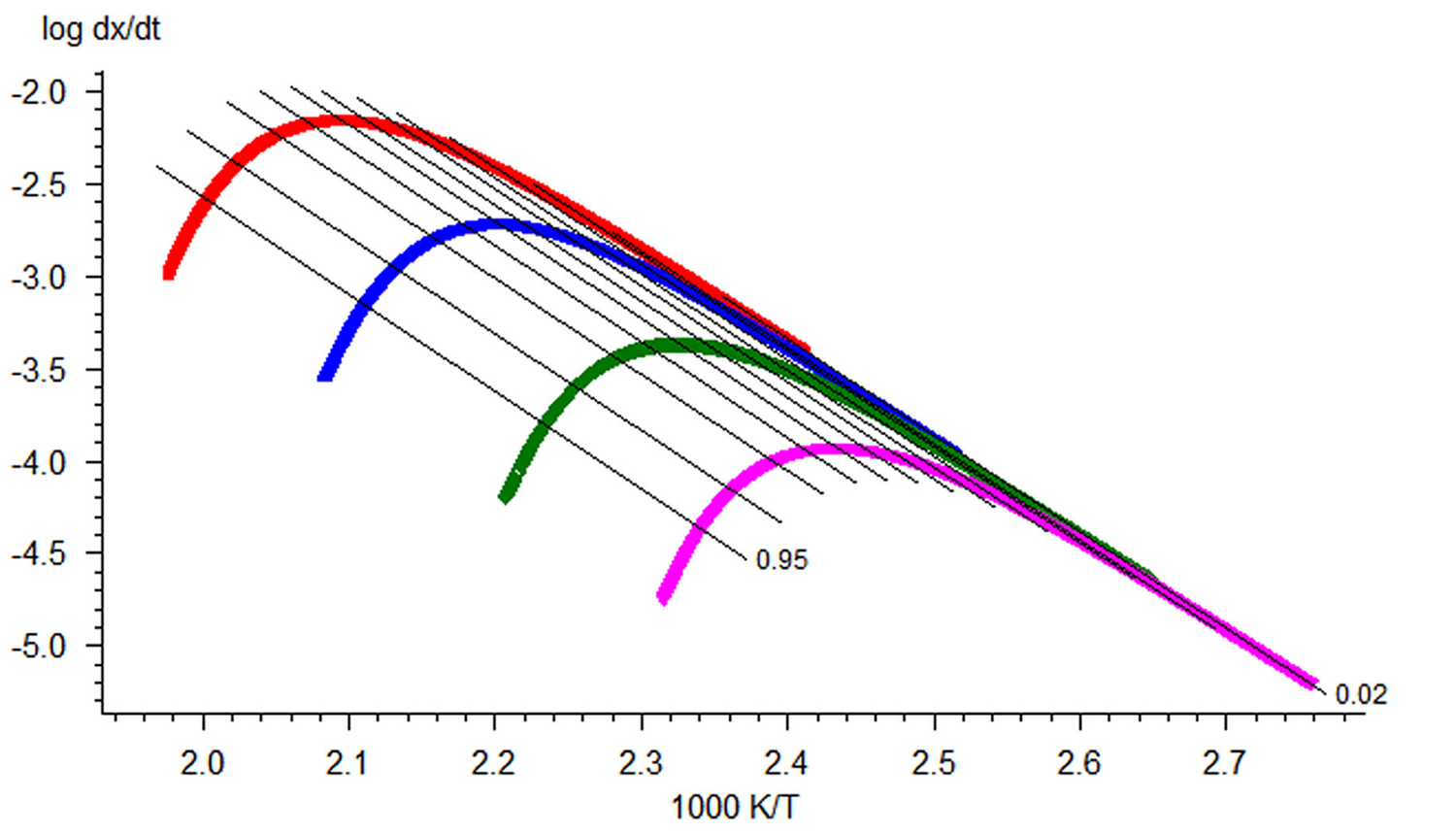
Fig. 3.1: Friedman analysis for the simulated set of data for heating rates of 0.25, 1.0, 5.0, and 20.0 K/min (Reprinted with permission from [9] © NETZSCH-Gerätebau GmbH).
Providing several measurements at different heating rates one can plot a linear dependence of the logarithm of rate on inverse temperature for given αi. As we notice above, Equation 1.4 can be easily linearized for any f(α) a linear dependence of the logarithm of rate on inverse temperature for given αi. In the Friedman method, the slope m = E/R of this line is found. Thus, the activation energy for each conversion rate can be calculated from the slope of the ln(dαi/dT) vs 1/T curve. The conversion rate on the left-hand side of the equation is found directly from the initial measured curve (e.g., thermogravimetric) by its differentiation with respect to time. This procedure is performed with the NETZSCH Proteus software used for processing the experimental data.
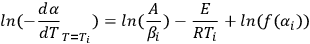
|
3.3 |
The second Arrhenius parameter, the logarithm of the preexponential factor, is also calculated from Equation 3.3.
Thus, the software allows the calculation of both Arrhenius parameters, the activation energy, and the logarithm of the preexponential factor. The calculation results are given in the tabulated form as the dependence of Arrhenius parameters on the conversion, as well as in the graphical form.
3.1.2 Ozawa–Flynn–Wall Method
The Ozawa method uses the integral dependence for solving Equation 1.3. Integration of the Arrhenius equation leads to Equation 3.4:
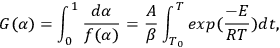
|
3.4 |
If T0 is lower than the temperature at which the reaction occurs actively, the lower integration limit can be taken as zero, T0 = 0, and after integration, Equation 3.5 takes the form of Equation 3.6:
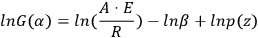
|
3.5 |
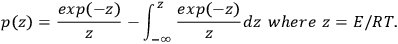
|
3.6 |
Analytical calculation of the integral in Equation 3.6 is impossible, therefore, it is determined as follows: Using the DOYLE approximation [7] (ln p(z) = –5.3305 + 1.052z), we reduce Equation 3.5 to Equation 3.7:
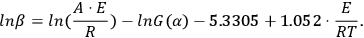
|
3.7 |
It follows from Equation 3.7 that, for a series of measurements with different heating rates at the fixed conversion value α=αk, the plot of the dependence
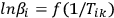
|
3.8 |
is a straight line with the slope m = –1.052 E/R. Tik is the temperature at which the conversion αk is achieved at the heating rate βi. It is evident that the slope of the linear dependence is directly proportional to the activation energy. If the activation energy has the same value at different αk values, we can state with confidence that the reaction is one-stage. Otherwise, a change in the activation energy with an increase in the conversion is evidence that the process is multistep. The separation of the variables in Equation 1.3 is thus impossible.
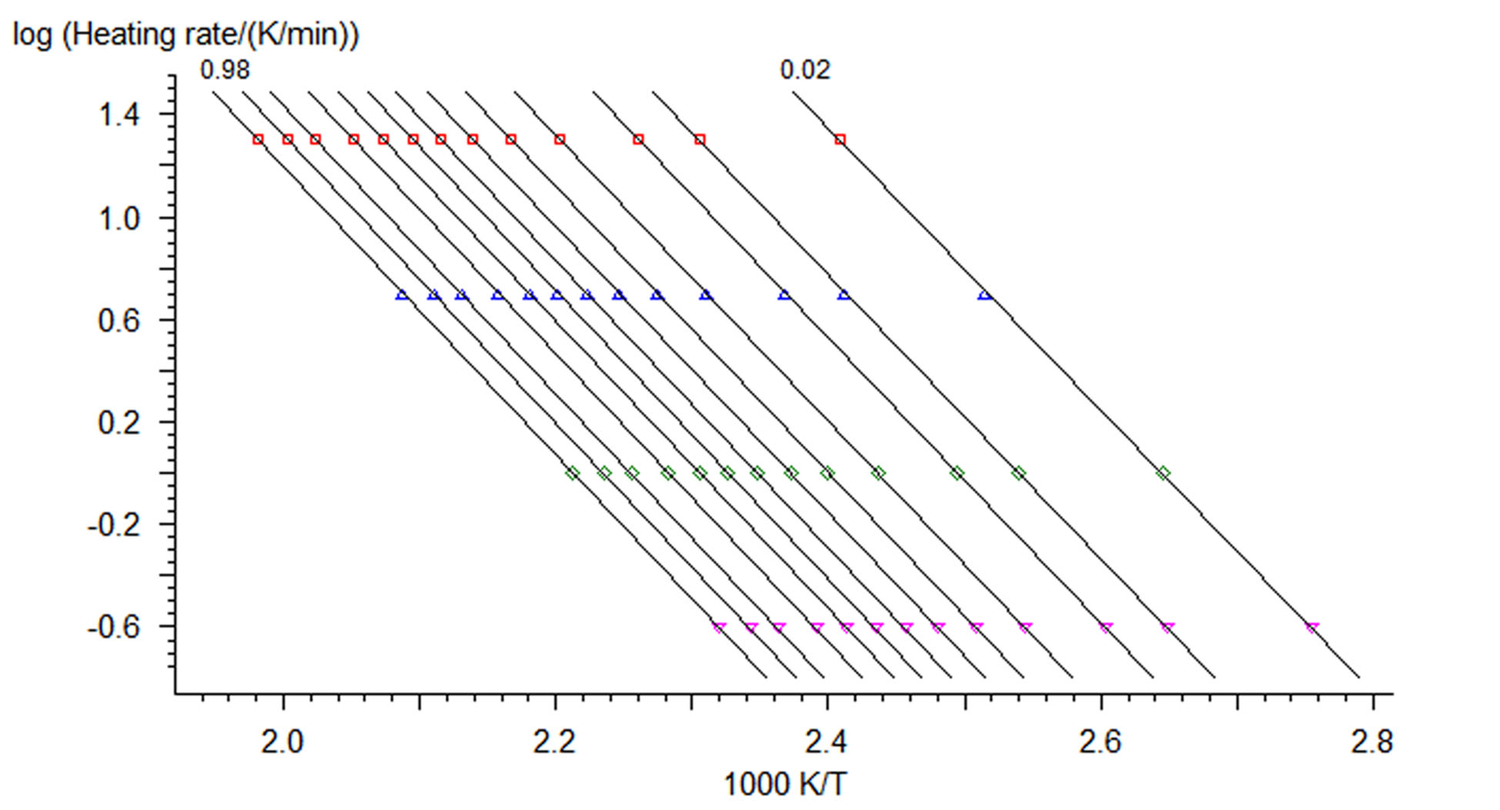
Fig. 3.2: Dependences of the logarithm of rate on inverse temperature according to the Ozawa–Flynn–Wall procedure (Reprinted with permission from [9] © NETZSCH-Gerätebau GmbH).
If E, αk, and zi are known, lnA can be calculated by Equation 3.9:
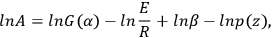
|
3.9 |
Figure 3.2 shows the plots of instantaneous rate versus inverse temperature obtained by this method. The resulting Arrhenius parameters are then used as a zero approximation in solving the direct kinetic problem.
The presence of several extreme points on the experimental TA curves is unambiguous evidence of the multistep character of the process. In this case, the use of the NETZSCH Peak Separation program makes it possible to separate individual stages and to estimate the Arrhenius parameters for each stage. The Peak Separation program is discussed below.
3.2 Direct Kinetic Problem
The direct kinetic problem is solved by the linear least-squares method for one-stage reactions or by the nonlinear least-squares method for multistage processes. For one-stage reactions, it is necessary to choose the type of function that best approximates (from the statistical viewpoint) the experimental curves for all heating rates used. The NETZSCH Thermokinetics software includes a set of basic equations describing the macrokinetics of processes to be analyzed [10].
Each stage of a process can correspond to one (or several) of the equations listed in Table 3.1. The type of f(α) function depends on the nature of the process and is usually selected a priori. For the users convenience, the notation of parameters and variables in Table 3.1 is the same as in the Thermokinetics software. Here, the p parameter corresponds to the conversion, p = α, and e = 1 – α.
If the type of function corresponding to the process under consideration is unknown, the program performs calculations for the entire set of functions presented in Table 3.1. Then, on the basis of statistical criteria, the function is selected that best approximates the experimental data.
This approach is a formal statistical-geometric method and, to a first approximation, the type of function approximating the experimental curves for all heating rates has no physical meaning. Even for quasi-one-stage processes where the chemical conversion stage has been separated, the equations presented in Table 3.1 can be correlated with a change in the morphology of the initial reagent, but no unambiguous conclusions can be drawn about the types of chemical transformations responsible for the nucleation of the reaction product. It often occurs that several functions adequately describe the experiment according to statistical
| Model abbreviation | f(e,p) | Reaction type |
|---|---|---|
| F1 | e | First order |
| F2 | e2 | Second order |
| Fn | en | nth order |
| D1 | 0.5/1-e | One-dimensional diffusion |
| D2 | -1/ln(e) | Two-dimensional diffusion |
| D3 | 1.5e1/3/(e-1/3-1) | Jander three-dimensional diffusion |
| D4 | 1.5/(e-1/3-1) | Ginstling–Brounshtein three-dimensional diffusion |
| R2 | 2e1/2 | Reaction on the two-dimensional interface |
| R3 | 3e2/3 | Reaction on the three-dimensional interface |
| B1 | ep | Autocatalysis according to the Prout–Tompkins equation |
| Bna | enpa | nth order autocatalysis according to the Prout–Tompkins equation |
| C1-X | e(1+KcatX) | First-order autocatalysis, X is the product in a complex model, often X = s |
| Cn-X | en(1+KcatX) | nth autocatalysis |
| A2 | 2e(-ln(e))1/2 | Two-dimensional nucleation (Avrami–Erofeev) |
| A3 | 3e(-ln(e))2/3 | Three-dimensional nucleation (Avrami–Erofeev)f |
| An | ne(-ln(e))(n-1)/n | n-Dimensional nucleation (Avrami–Erofeev) |
Tab. 3.1: Reaction types and corresponding type of function f(α) in Equation 1.2) [10].
criteria. The choice of the function is based on the search for the physical meaning of the resulting relation. In this context, some a priori ideas are used concerning the mechanisms of possible processes in the system under consideration. This can be literature data, results of other physicochemical studies, or general considerations based on the theories of heterogeneous processes. However, similar kinetic analysis provides a better insight into the effect of various external factors on the change in the morphology of the initial reagent and on the course of the process as a whole. Let us consider in detail the procedure of kinetic analysis based on the thermoanalytical experimental data for the dehydration of calcium oxalate monohydrate (CaC2O4 ∙ H2O).
